活用“两差”辨“稳定”

文／李海宁

“两差”即极差、方差，它们以不同的方式刻画一组数据的离散程度。极差可以反映一组数据的变化范围，方差则能反映一组数据偏离平均值的程度。这“两差”都展现了数据之间的差异，描绘了数据的波动情况，即数据的离散程度。它们是初中统计学知识的重要内容，广泛应用于生活。

一、极差的应用

例1某市5月25日—5月29日的气温情况如下：

请对该市这5天的日温差情况进行分析。

解：5月25日的温差是23-21=2（℃），5月26日的温差是25-22=3（℃），5月27日的温差是23-15=8（℃），5月28日的温差是25-15=10（℃），5月29日的温差是24-17=7（℃）。所以这5天的日温差先逐渐增大再减小，相对来说5月25日与5月26日的气温较稳定。

【点评】计算日温差是一个典型的极差应用的例子。因为极差只是利用了一组数据中的最大值和最小值，不能反映数据整体的离散程度，所以提供的只是数据粗略的离散情况。

二、方差的应用

例2为考察甲、乙两种小麦长势，农技人员在同一时期分别从两块试验田中随机抽取6棵麦苗植株，并标号为1～6，将测得的苗高数据绘制成统计图。请你根据统计图所提供的数据，计算甲、乙两种麦苗高度的平均数和方差，并比较这两种麦苗的长势。

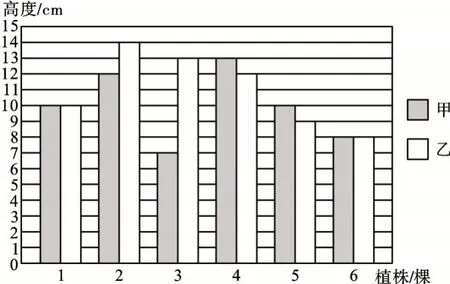
【点评】比较两种麦苗的长势不能仅考量数据的极端值，还应该关联每一个数据，更精确地考量这组数据的离散程度（波动情况）。

三、“两差”的综合应用

例3甲、乙两人在相同的情况下各打靶10次，打靶成绩（单位：环）如图所示：

（1）填表：

甲乙极差（环） 平均数（环） 方差（环2）

（2）从不同的角度评价甲、乙两人打靶的成绩。

解：（1）

甲乙极差（环）4 8平均数（环）7 7方差（环2）1.2 5.4

（2）本题答案不唯一，下列解法供参考。

例如：

①甲、乙打靶的成绩的平均数都是7环，说明两人的打靶实力相当。

②甲、乙两人打靶的成绩的极差分别是4环和8环，说明甲打靶成绩的波动范围较小；甲、乙两人打靶的成绩的方差分别是1.2环2和5.4环2，说明甲打靶的成绩更稳定。

③甲、乙命中9环及9环以上的次数分别是1次和3次，说明乙命中9环及9环以上的次数更多，更有潜力。

【点评】在实际问题中，极差与方差都是表示一组数据离散程度的统计量，都能反映数据的稳定性。但两者还是有区别的，极差只是反映出一组数据大致的波动范围，而方差关联每个数据，能更精确地反映问题。我们在面对具体问题时要灵活选用。