欧几里得证法中的双模型

文／江苏省苏州市阳山实验初级中学校 陈一鑫 马天宇

勾股定理是初中几何中的重要定理之一，目前约有500 种证明方法，由此我们可以看出勾股定理的魅力之大。据数学史料记载，我国周朝数学家商高提出“勾三、股四、弦五”，这说明我国在很早的时候就有人发现了勾股定理。而西方最早提出并证明勾股定理的是公元前6 世纪的古希腊毕达哥拉斯学派，所以勾股定理在西方也被称为“毕达哥拉斯定理”。

古希腊数学家欧几里得曾在其著作《几何原本》中给出勾股定理的证明方法，该方法在“命题47”中呈现，我们一般称其为欧几里得证法。具体的证明过程同学们可以见教材第88 页中的内容——“勾股定理的证明”。

在欧几里得证法中，我发现了几何中经常用到的两个数学模型，一个是“手拉手”模型，另一个是“平行等积”模型。

如图1，当AB=BF，BC=BD，并且它们的夹角∠ABF和∠CBD相等时，就能证得△ABD≌△FBC，这就是我们常用的“手拉手”模型。

图1

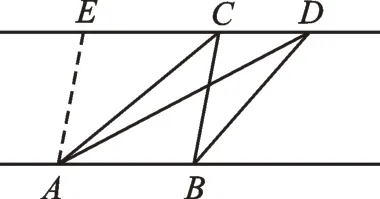
图2

如图2，当AB∥CD时，易得S△ABC=S△ABD，这就是“平行等积”模型。我们在很多问题中会用到这个数学模型。进一步研究，我们发现，若AE∥BC，则四边形ABCE为平行四边形，则可证得

在欧几里得证法中，就用到了以上两个非常重要的数学模型。如果我们对这两个数学模型非常熟悉的话，那么再去理解欧几里得证法就很容易了。

教师点评

勾股定理的证法有很多种，对于初中生而言，简洁、优美并且有代表性的证法不是很多。欧几里得证法是非常有代表性，并且是很有思维训练价值的证法，但很多初中生感觉这种证法很难理解和掌握。两位同学正是基于这样的思考，从基本数学模型的视角分析欧几里得证法。我相信他们的解读会帮助同学们更好地理解和掌握欧几里得证法，并运用这两种数学模型解决更多的问题。