交叉隧道爆破振速回归分析及对比研究

赵 岩，王小敬，王海龙，王东升

(1.中国矿业大学(北京) 力学与建筑工程学院， 北京 100083；2. 北旺集团有限公司，河北 承德 067400；3. 河北省装配式建造与地下工程技术创新中心，河北 承德 067400；4. 河北省土木工程诊断、改造与抗灾重点试验室，河北 张家口 075000)

爆破施工作业因其经济效益好、工作效率高、操作易行等优点已被广泛应用于隧道掘进、矿山开采、边坡开挖等各种土建工程中。然而，施工引起的爆破振动对在建工程及周边构筑物均会造成不利影响[1-3]。实际操作中，大多研究人员通过现场实测[4-5]展开爆破振动研究工作，并利用回归分析的方法研究爆破振动衰减规律。贾海鹏等[6]利用萨道夫斯基公式研究隧道中夹岩层爆破振动规律，并利用数值模拟验证了结论的可靠性；王海龙等[7]通过最小二乘法处理现场实测数据，对不同围岩等级进行分类研究；吕涛等[8]通过比较线性回归及非线性回归的异同，证明非线性回归在确定爆破振动衰减参数的准确性更高；何理等[9]运用量纲分析得到可以反映边坡高程放大效应的模型方程，取得了良好的拟合精度；Jiang等[10]利用模糊神经推理系统对爆破施工引起的地面振动进行了预测；Tian等[11]利用最小二乘拟合及小波包分析相结合的方式研究了爆破振动在地层中的传播规律。

近年来，智能算法之一的粒子群优化(particle swarm optimization)也被应用到爆破振动衰减参数的确定中，并被证实其得到的拟合效果优于大多数回归分析方法：张乐文等[12-13]通过小波降噪及粒子群优化进行拟合分析，结果表明降噪处理可以提高萨式的拟合效果； Hasanipanah等[14]分别以线性函数与幂函数作为适应度函数进行粒子群优化，结果表明适应度函数为幂函数的拟合效果更好。

萨道夫斯基公式对平整地面上的爆破振动速度拟合效果良好，但对具有高程差的爆破工程预测效果并不理想。许多学者针对这一问题进行了优化研究。唐海等[15]依托采石场及核电站爆破工程，得到可以反映实际工程的爆破振动衰减模型；周文海等[16]以边坡抛掷爆破为工程背景，利用数值积分及无量纲化相结合的方法得到反映边坡爆破振动规律的回归方程；何理等[17]利用量纲分析及小波包分析相结合的方法，对隧道与露天边坡协同爆破的振动衰减规律进行了研究；樊祥喜等[18]引入等效药量及等效爆心距的概念对隧道爆破引起的路基振动进行了分析。

为满足交通选线需要，交叉隧道等复杂隧道形式被广泛应用于实际工程中，露天爆破得到的爆破振动预测公式并不适用于隧道爆破工程。基于此，本文依托立体交叉隧道工程，引入一种以粒子群优化为计算主体的回归分析方法，并通过量纲分析得到可以反映交叉隧道爆破振动规律的拟合模型。

1 粒子群优化算法

粒子群优化算法是用来模拟鸟类聚集和鱼类繁殖等生物社会行为，可以用来寻找问题的最优解。该算法由一群散体粒子组成，这些粒子可以根据最佳解决问题方案搜索个体最佳位置(pbest)和全局最佳位置(gbest)。换言之，即，每个粒子均会朝着个体最佳(pbest)与全局最佳(gbest)的方向进行移动。每次迭代计算都是根据粒子的位置和速度进行更新，其运动更新过程可以表示如下：

(1)

式中：νi、xi分别为第i个粒子的速度及位置；ω为惯性权重，用来体现以前例子速度对当前粒子速度的实时影响；c1和c2为学习因子;r1和r2为[0,1]之间的均匀随机数。式(1)为标准粒子群算法的表达形式。

2 工程概况及测点布置

新建京张高铁隧道(简称为新建隧道)DK173+862～DK174+057 段下穿既有重载铁路(简称为既有隧道)，形成立体交叉隧道，对应既有隧道实际里程IDK25+620，两条隧道均为单洞双线铁路隧道。交叉隧道平面交角为76°22′，两隧道之间的最小垂直距离为16 m。中夹岩层主要由凝灰岩、凝灰质熔岩，全～强风化凝灰岩组成，凝灰岩遇水后力学性质会出现较大幅度劣化，给交叉隧道爆破施工带来了一定的困难[19-20]。交叉隧道平面位置如图1所示。

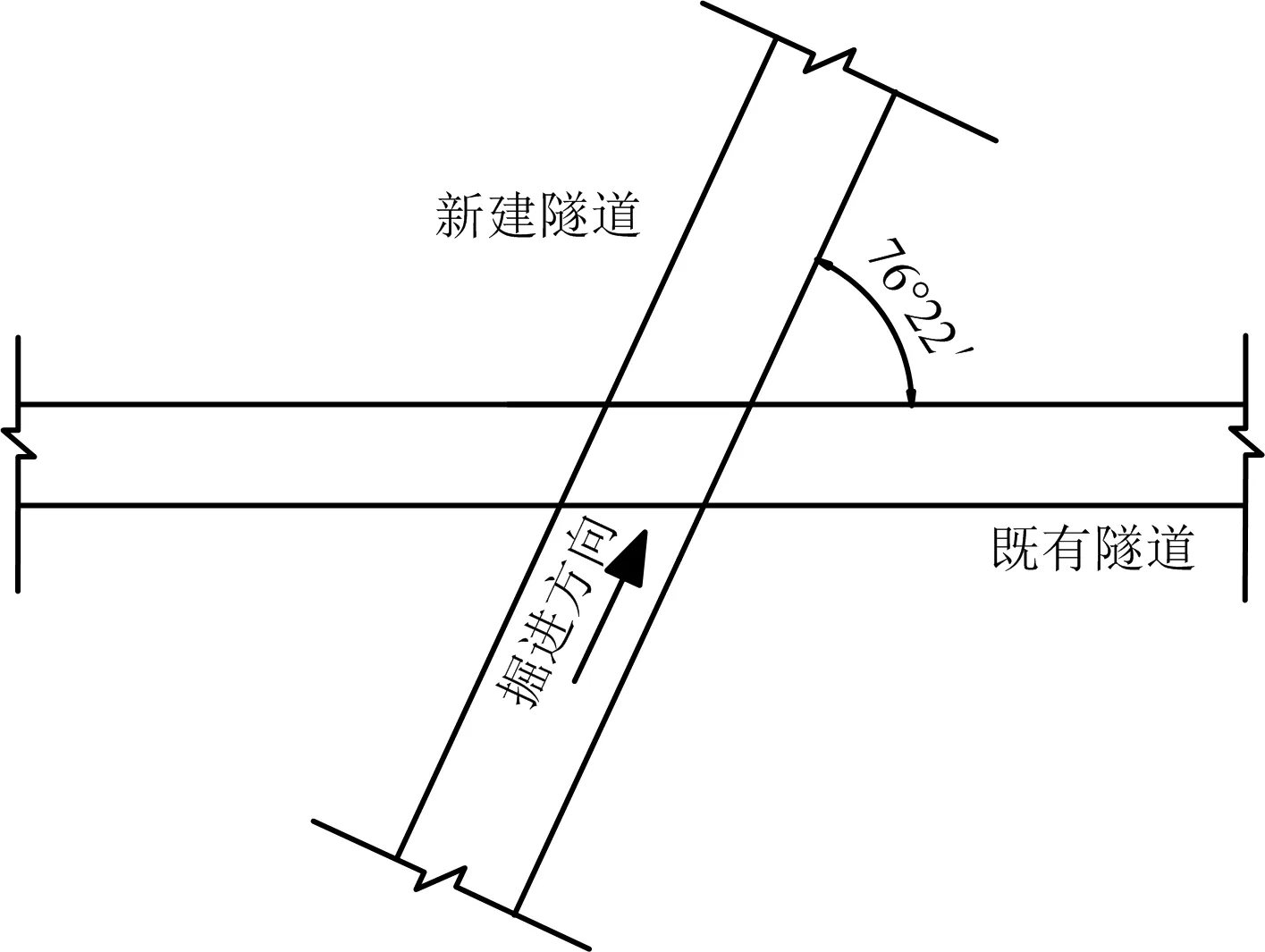
图1 交叉隧道平面布置 Fig.1 Layout of crossing tunnel

新建隧道掘进至交叉区域之前，利用既有隧道运营天窗，布置监测仪器、组建光纤通讯系统和设备组网，完成自动化监测。本次监测采用中科测控公司研发的TC-4850爆破振动测振仪，该爆破测振仪配有3个特定通道，且均配置有可以采集x、y、z3个方向的爆破振速传感器，可对每个方向的爆破振速进行监测。TC-4850N系统传输速率极高，通过相配套的分析软件可以实现远程控制。

监测点布置于既有隧道边墙表面，共布置5个测点(见图2)。现场安装过程中，速度传感器x方向指向既有隧道洞口方向，y方向指向隧道直径内部，z方向则垂直于xy平面向上。

图2 测点布置

3 爆破振动回归分析

研究显示[2,6,20]，由于隧道掌子面前方自由面数量少于掌子面后方，掌子面前方引起的爆破振动速度大于掌子面后方。因此，本文选取掌子面未达到交叉断面时，既有隧道中测点3的爆破振动速度进行研究，具体爆破参数及爆破处理结果如表1所示。

表1 既有隧道交叉点爆破振动速度

交叉隧道爆破振动速度的影响因素主要包括爆破施工参数、围岩岩体的物理力学特性、掌子面与交叉断面的距离、交叉隧道高程差及爆心距等，现将影响交叉隧道爆破振速的物理量归纳为14个(见表2)。

表2 影响爆破振速的物理量

爆破振动速度与相关物理量的函数关系表示如下：

v=φ(v1,Q,Q0,ρ,E,σ,μ,D,H,R,E0,f,S,a)

(2)

选取v1、R及Q为基本独立量纲，根据量纲分析原理，上述函数关系可以用12个无量纲数Π表示：

(3)

因此，爆破振动速度的函数关系可以表示为

Π1=κ(Π2,Π3,Π4,Π5,Π6,Π7,Π8,Π9,Π10,Π11,Π12)

(4)

根据量纲分析原理可知，不同无量纲数的乘积或者乘方仍为无量纲数[21]。因此，令：

(5)

即，

(6)

(7)

式中：K为与Q、H、D、f相关的场地系数；β1、β2、β3、β4分别为Q、H、D、f相关的衰减系数。

爆破振动频率与爆破药量、爆破规模，隧道围岩岩体性质等因素相关，一定爆破药量下的爆破振动频率可以表示为如下[22]

(8)

式中：ξ、α为待定系数，其他参数同前。

联立式(7)、式(8)，可得：

(9)

依据粒子群优化原理，首先需要确定适应度函数，本文选择适应度函数的目的是为了使实测数据与回归拟合值的误差最小。因此，适应度函数可以选取如下：

(10)

式中：vi为实测爆破振速；n为实测数据个数。

(11)

由拟合效果(见图3)可知，回归模型的相关系数平方(r2)为0.998 2，对所述实测隧道爆破振动速度具有良好的拟合效果。

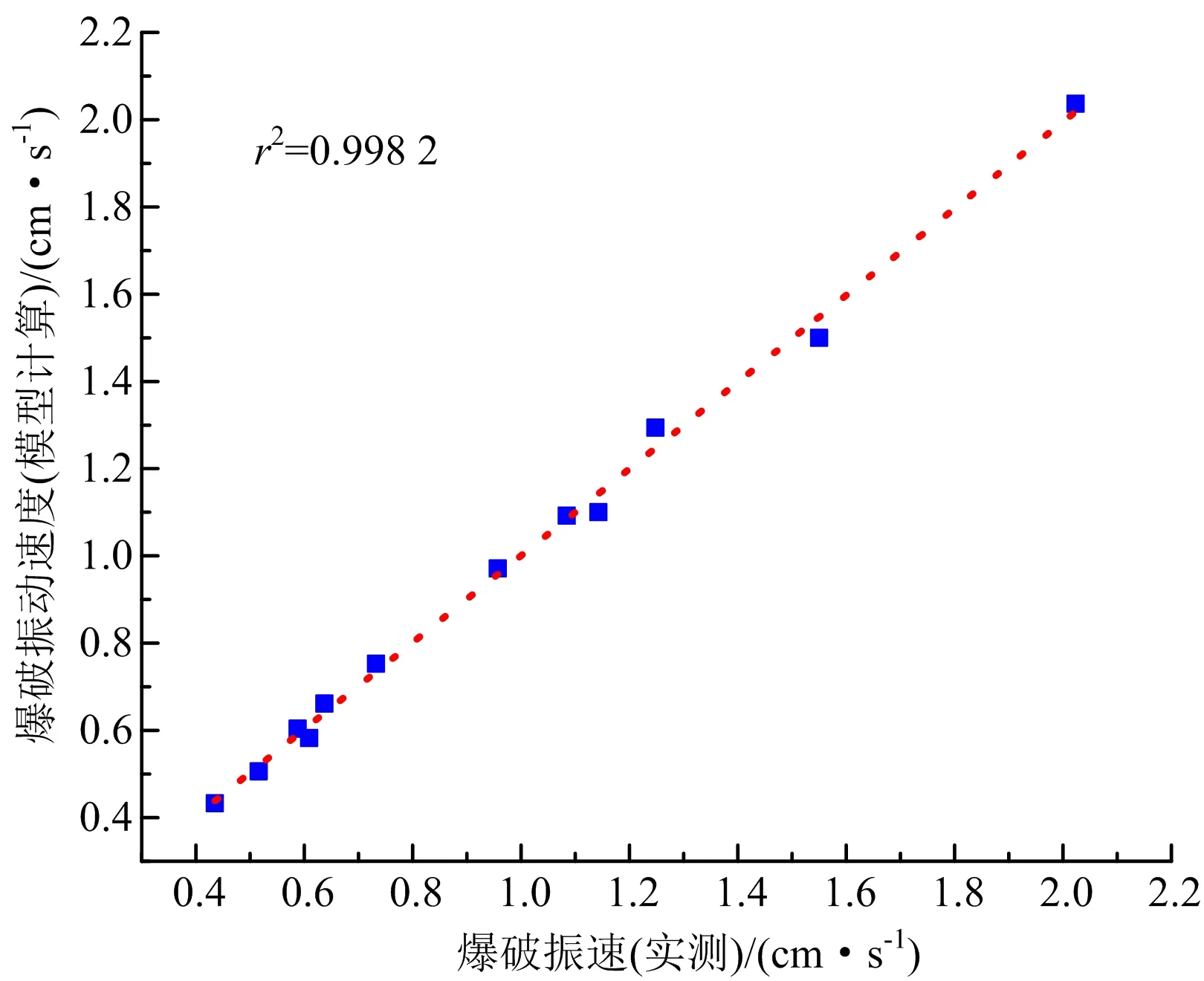
图3 模型回归分析拟合效果

4 回归分析效果评价

为验证本文引入的回归分析方法的可行性，利用现有拟合模型对交叉隧道爆破振动实测数据进行分析，对比不同模型的拟合效果。不同回归模型的拟合效果如表3所示。其中，相关系数的平方(r2)越接近1，残差平方和(SSE)越小，拟合效果越好。

表3 不同拟合模型的分析效果

为更加直观地体现不同计算模型的拟合效果，将表3中的统计性参数绘制成柱状图，结果如图4所示。结合表3及图4可知，模型Ⅰ 模型Ⅱ、模型Ⅲ、模型Ⅳ及模型Ⅷ的相关系数(r2)均小于0.9，拟合效果并不理想，模型Ⅴ、模型Ⅵ及模型Ⅶ的相关系数(r2)均超过0.9，但均小于本文模型Ⅸ得到的0.998 2；与r2的分析方法类似，模型Ⅰ 模型Ⅱ、模型Ⅲ、模型Ⅳ及模型Ⅷ得到残差平方和(SSE)均大于0.250，预测精度较低，模型Ⅴ、模型Ⅵ及模型Ⅶ的相关系数(r2)均在0.160以下，但均大于本文模型Ⅸ得到的0.009。上述对比结果说明，无论是从r2或者SSE的角度对比，本文拟合模型的振动预测精度均为最佳，证明引入的耦合回归分析方法，可以真实有效反映交叉隧道地形地质条件对爆破振动衰减的影响规律。

5 结论

1)通过粒子群优化及量纲分析可以得到爆破振动速度衰减模型中的待定参数，拟合结果表明具有良好的预测精度，可以为类似近接隧道爆破振动预测提供理论借鉴。

2)与其他爆破振动预测模型相比，文章中提及的拟合模型得到的相关系数(r2)为0.998 2，均大于其他拟合模型，拟合效果理想；残差平方和(SSE)为0.009，预测精度最佳，可以较准确地反映地形条件对隧道爆破振动衰减的影响规律。本文引入的集成分析思路可以被应用于其他近接隧道控制爆破应用中。