琼州海峡客滚船渡海车辆配载优化决策研究

陈 宁，吕 鹏，胡 斌

(1.武汉理工大学 交通与物流工程学院，湖北 武汉 430063；2.武汉理工大学海南研究院，海南 三亚 572025；3.华中科技大学 管理学院，湖北 武汉 430071)

随着海南省自由贸易港建设的持续推进，作为海南省与内地交流的“黄金水道”，琼州海峡的客货运量未来将会激增，而作为琼州海峡运输体系中的一种重要运输方式——客货滚装运输，将扮演越来越重要的角色。虽然当前一些智能化售票手段已经运用到客滚轮渡的日常业务管理中，但客滚运输业务中的客滚船配载决策过程多依赖人工经验，其配载效率有待进一步提高，无法满足节假日和极端天气影响下的疏港要求及智慧港口的发展要求。

客滚船配载有其独特性，其装载对象为社会渡海车辆和过海旅客，在此仅考虑车辆的配载问题，渡海车辆的种类和车型繁杂，各类车辆尺寸相差较大，配载时为充分利用船舱面积，需考虑车辆的长宽，客滚船在配载约束上呈现矩形件排样特性，因此笔者引入矩形件排样优化理论，已有的滚装船配载优化理论对于客滚船配载优化决策难以沿用。目前，国外对于客滚船渡海车辆配载优化研究较少，大多是针对客滚船配载安全性、装卸效率、客滚船装卸载硬件系统的开发等方面进行研究[1-2]。国内对于滚装船配载研究有一定的理论基础，但是大多数是针对传统滚装船的配载优化及优化配载系统的实现[3]、多层滚装船的配载优化[4]，多装卸货港的滚装船配载[5]；而在客滚船研究方面，吴兵等[6]对客滚船载运电动汽车火灾风险进行了相关研究，并结合客滚船的特点，提出相应的安全管理对策；张煜等[7-8]认为客滚船配载带有二维装箱特性，分别对离线和在线两个状态下的客滚船配载优化进行研究，实现了不同规模下客滚船的有效配载；ZHANG等[9]基于客滚船配载的二维装箱特性，考虑车辆的复杂旋转特性及安全航行的情况下的客滚船配载方法。对于矩形排样优化理论研究也较为成熟，在服装排料[10]、港口堆场布局[11]等问题上均有应用。

故笔者结合客滚船配载实际及其矩形件排样特性，构建客滚船配载优化决策模型，设计融合最低水平线算法和基于K-邻域搜索的遗传算法的求解方案，通过模拟不同场景下的配载过程来验证模型及求解方案的有效性，为琼州海峡新海港客滚船配载的优化决策提供参考。

1 问题描述

客滚船配载问题与矩形件排样问题如图1所示，将车辆视为矩形件，客滚船船舱甲板视为长宽固定的板材，客滚船配载的矩形件排样特性体现在：①待渡车辆进入船舱时，不用考虑车辆高度对于配载的影响，只需考虑车长和车宽的影响，且无需考虑预设的车道线对于车辆位置的限制，呈现二维约束限制，与矩形件排样优化问题在维度上保持一致；②车辆间无干涉，同一位置仅能停放一辆车辆，与矩形件排样优化问题中矩形件之间无干涉放置规则保持一致；③客滚船的单层甲板长度固定，且仅能装载部分待渡车辆进入甲板，直至甲板面积得到充分利用，与矩形件排样优化问题选取物品的规则及目标一致。

图1 客滚船配载问题与矩形件排样问题

实际上，为了保证船舶航行安全和装载车辆的安全，客滚船在配载过程中必须充分考虑船舶的稳性安全、船舶额定载重量、车辆间及车辆与舱壁间的安全距离等现实约束。

此外，为解决港口在极端天气影响下导致的车辆积压问题，将车辆和旅客尽可能地高效疏港，在考虑配载决策时，以船舱满舱为目标，不仅能够提高疏港效率，同时可以在一定程度上保证单航次收益。故笔者基于矩形件排样优化特性并保证船舶安全航行的现实约束条件下，以船舱甲板面积利用率最大为目标，构建客滚船配载优化模型。

2 模型构建

2.1 问题假设

(1)假设客滚船船舱及渡海车辆均为形状规则、质量均匀的矩形，且已知所有渡海车辆的信息。

(2)假设以客滚船舶的船舱俯视图可配载区域的左下角为原点建立如图2所示的xOy坐标系，船头左端点为O点，船头至船尾为y轴，船舶从左至右为x轴。车辆以左下角坐标为位置标识，即车辆配入船舱后，车辆左下角的坐标(xi,yi)。

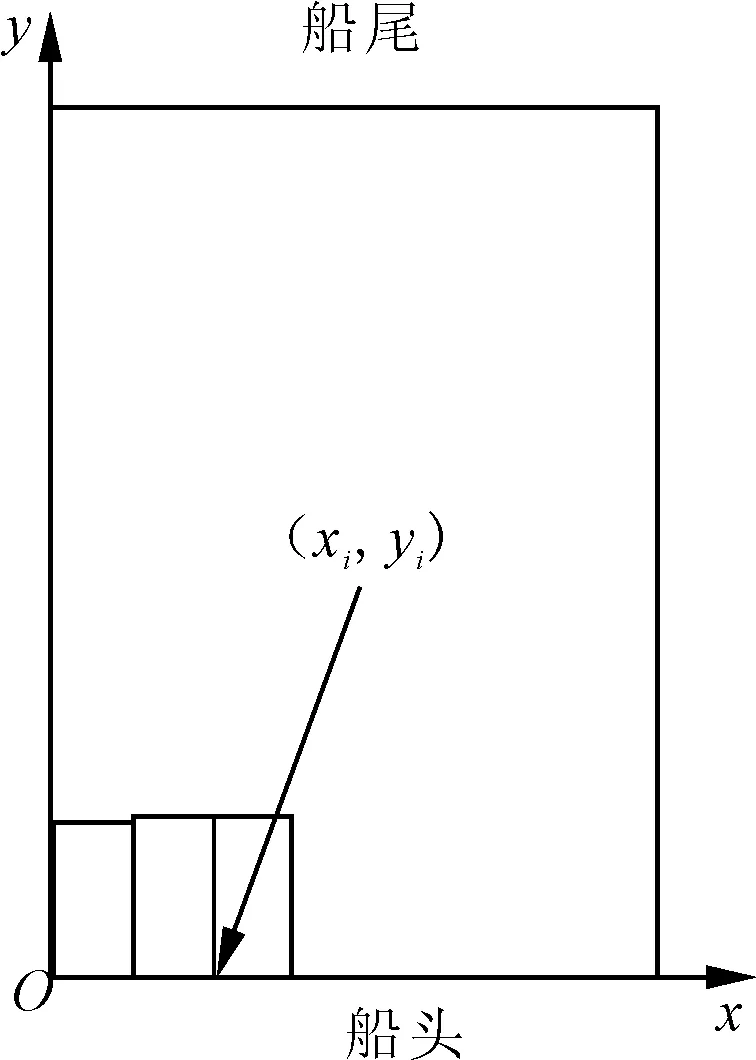
图2 船舶坐标系示意图

2.2 模型建立

(1)集合。以渡海车辆从闸口进入待渡场的顺序进行标号排序，I={i|i=1,2,…,|I|}。

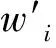
(3)变量。Eij为0-1变量，车辆i在车辆j的左侧则为1，否则为0，即xi+wi≤xj；Fij为0-1变量，车辆i在车辆j的下侧则为1，否则为0，即yi+li≤yj；zi为0-1变量，选择第i辆车配入船舱为1，否则为0。

因此，构建如下客滚船配载优化模型：

(1)

Eij+Eji+Fij+Fji+(1-zi)+(1-zj)≥1

∀i≠j,i，j∈I

(2)

xi+wi≤xj+R(1-Eij+2-zi-zj)

∀i≠j,i，j∈I

(3)

yi+li≤yj+R(1-Fij+2-zi-zj)

∀i≠j,i，j∈I

(4)

xi+wi≤W+R(1-zi)

(5)

yi+li≤L+R(1-zi)

(6)

(7)

(8)

(9)

xi,yi∈N+∀i∈I

(10)

Eij,Fij∈{0,1} ∀i≠j,i，j∈I

(11)

zi∈{0,1} ∀i∈I

(12)

(13)

(14)

式(1)为目标函数，配载上船的所有车辆的总面积与客滚船船舱可装载的甲板区域面积的比值，即模型目标使得客滚船船舱可装载的甲板区域面积利用率最大。式(2)～式(6)为矩形件排样约束：式(2)～式(4)保证车辆头部均与船头同向，顺直停放在甲板上，同时车辆与车辆间无干涉，独立停放；式(5)及式(6)保证车辆完全停放在车舱内，无溢出现象。式(7)～式(9)为现实约束，即保证船舶安全航行：式(7)保证所有装入船舱的车辆的总重量应小于船舶额定载重量的90%；式(8)及式(9)保证在装入所有车辆后，船舶的纵横倾约束在安全的额定范围内。式(10)～式(12)为变量取值范围，式(13)为所有上船渡海车辆面积累加所得的总面积不超过船舱甲板可载面积，式(14)为所有上船渡海车辆的总价值。

3 算法设计

3.1 算法整体架构

基于客滚船配载问题特性，设计K-邻域搜索的遗传算法，以此确定渡海车辆的上船顺序，以及最低水平线算法，确定车辆停放在船舱甲板上的具体位置，融合最低水平线算法和K-邻域搜索的遗传算法作为客滚船配载优化决策问题的求解算法，具体算法流程如图3所示。

图3 客滚船配载优化决策算法流程图

3.2 K-邻域搜索的遗传算法

遗传算法局部空间搜索能力较差,导致进化后期搜索效率偏低，解质量不高，故引入局部搜索算法解决遗传算法的早熟收敛问题，从而提高解的质量。基于K-邻域搜索的混合遗传算法是综合遗传算法和邻域搜索算法各自优势的全局搜索算法，它一方面保留了遗传算法的全局搜索能力，同时基于邻域搜索提高了遗传算法的局部搜索能力。

(1)编码。选用整数顺序编码的方法，以车辆到达待渡场的顺序对每一辆待渡车辆进行编号，假设生成的染色体为56412387，则表示车辆上船的顺序依次为5、6、4、1、2、3、8、7。

(2)种群初始化。种群初始化的策略采用随机生成法及经验选择两种初始化种群策略结合的方法。

(5)交叉及变异操作。分别采用顺序交叉法(OX)及逆序变异法，交叉概率pc和变异概率pm通过多次实验和前人经验来确定。

(6)K-近邻域搜索。①邻域搜索。当算法迭代停滞若干代或者迭代完成后并生成一个最优解时，对最优解进行邻域搜索，对最优解的所有渡海车辆的编码依次进行减一、加一操作，并对新个体逐个判断，观察其适应度，对比原个体对应解的适应度是否提高了，若新个体对应解的适应度大于原最优解的适应度，则舍弃原最优解，保留新的最优解，否则保留原最优解。邻域搜索能够有效改善遗传算法对于局部搜索能力差的不足之处。②K-近邻点集。利用遗传算法对NPC问题进行求解时，在对遗传算子进行不同的改进后，解的质量大多能够得到有效提高，然而，其求解效率比较低，特别是当问题规模增大，算法迭代寻求最优解的时间也在不断增加，为提高基于邻域搜索的混合遗传算法迭代寻求最优解的效率，参考文献[12]，结合K-近邻点集进一步对算法进行优化，经多次试验，当K取10时，问题求解效果较好。

(7)终止条件。重复以上的各种遗传进化操作后，直到适应度函数值达到期望值，即当前客滚船配载方案中船舱的面积利用率达到了期望值，即算法终止，输出最佳客滚船配载方案。

3.3 最低水平算法

笔者引入矩形件排样问题中矩形件的定位算法确定待渡车辆在船舱甲板的具体位置，基于客滚船实际选择采用最低水平线算法为车辆定位算法。具体算法流程如下。

(1)对于在待渡场等待上船的待渡车辆的序列I={I1，I2，…，In}，要将它们引导至客滚船甲板上，并安排合理的位置，客滚船可配载区域长为L，宽为W，其中第i辆车的长度和宽度分别为li,wi，i=1,2,…,n。甲板左下角即为原点，坐标(0，0)，车辆在甲板上的具体位置由车辆左下角坐标唯一确定。

②产品展示形象生动。以GIS地图作为展示应用平台，各类气象信息产品由图片转变为GIS图层展现应用，在Web浏览器中实现了产品图像的透明化处理及放大、漫游、定位、测距、地理信息查询等空间查询应用功能，并实现了展现内容随图像放大逐步细化显示的功能。

(2)在引导车辆上船前，首先初始化甲板最低水平线集合。设水平线集合为λ={λ1,λ2,…,λn}，水平线用λi=(ri,si,ti)表示，ri表示水平线λi的左端端点，si表示水平线λi的右端端点，ti表示水平线λi的高度，即水平线λi与x轴的垂直距离。

(3)初始状态下，集合λ中仅有一个元素，即甲板的内舱壁，此时为最低水平线，λ1=(0，W,0)。在第一次装车时，选择待渡车辆的序列中的第一辆车I1，从水平线λi集合中选择λ1，将车辆I1的宽度与水平线λi的宽度进行比较，若wi≤W，表明车辆I1可以停放在水平线λ1后。

(4)当车辆I1停放好后，将车辆I1的车尾处的水平线λ2更新至λ集合中，并将车辆I1从I={I1，I2，…，In}剔除，此时λ集合中含有两个元素，即两条水平线λ1，λ2，λ1=(w1,W,0)，λ2=(0，w1,l1)。

(5)在配载第二辆车的时候，从所有待渡车辆选择第二辆渡海车辆I2进行配载时，从λ水平线集合中选择高度最低的一条水平线λ1，λ1为λ水平线集合高度最小的水平线，比较渡海车辆I2的车身宽度w2和λ1的宽度W-w1的大小，若w2≤W-w1，即代表渡海车辆I2可以放在新的水平线λ1的后，并停放在水平线λ1的最左端；

(6)如图4(a)所示，在对车辆Ii选择合适位置时，当前水平线集合为λ={λ1,λ2,λ3,λ4,λ5}，λ1=(r1,s1,t1)，λ2=(r2,s2,t2)，λ3=(r3,s3,t3)，λ4=(r4,s4,t4)，λ5=(r5,s5,t5)，车辆Ii的长宽为li、wi。首先选择5条水平线中高度最低的水平线λ5，将车辆Ii的宽度wi与s5-r5进行比较。若wi≤s5-r5，则将车辆Ii停放在水平线λ5处；若wi>s5-r5，则舍弃水平线λ5，则从λ={λ1,λ2,λ3,λ4,λ5}挑选高度次低的水平线λ2。继续将车辆Ii的宽度wi与水平线λ2的宽度s2-r2进行比较，若wi≤s2-r2，则将车辆Ii停放在水平线λ2处；若wi>s2-r2，则舍弃水平线λ2，则从λ={λ1,λ2,λ3,λ4,λ5}挑选高度再次低的水平线λ4，继续将车辆Ii的宽度wi与水平线λ4的宽度s4-r4进行比较，经过比较，车辆Ii的宽度wi与水平线λ4的宽度s4-r4满足wi≤s2-r2的条件，即将车辆Ii停放在水平线λ4后，并靠左放置，如图4(b)所示。

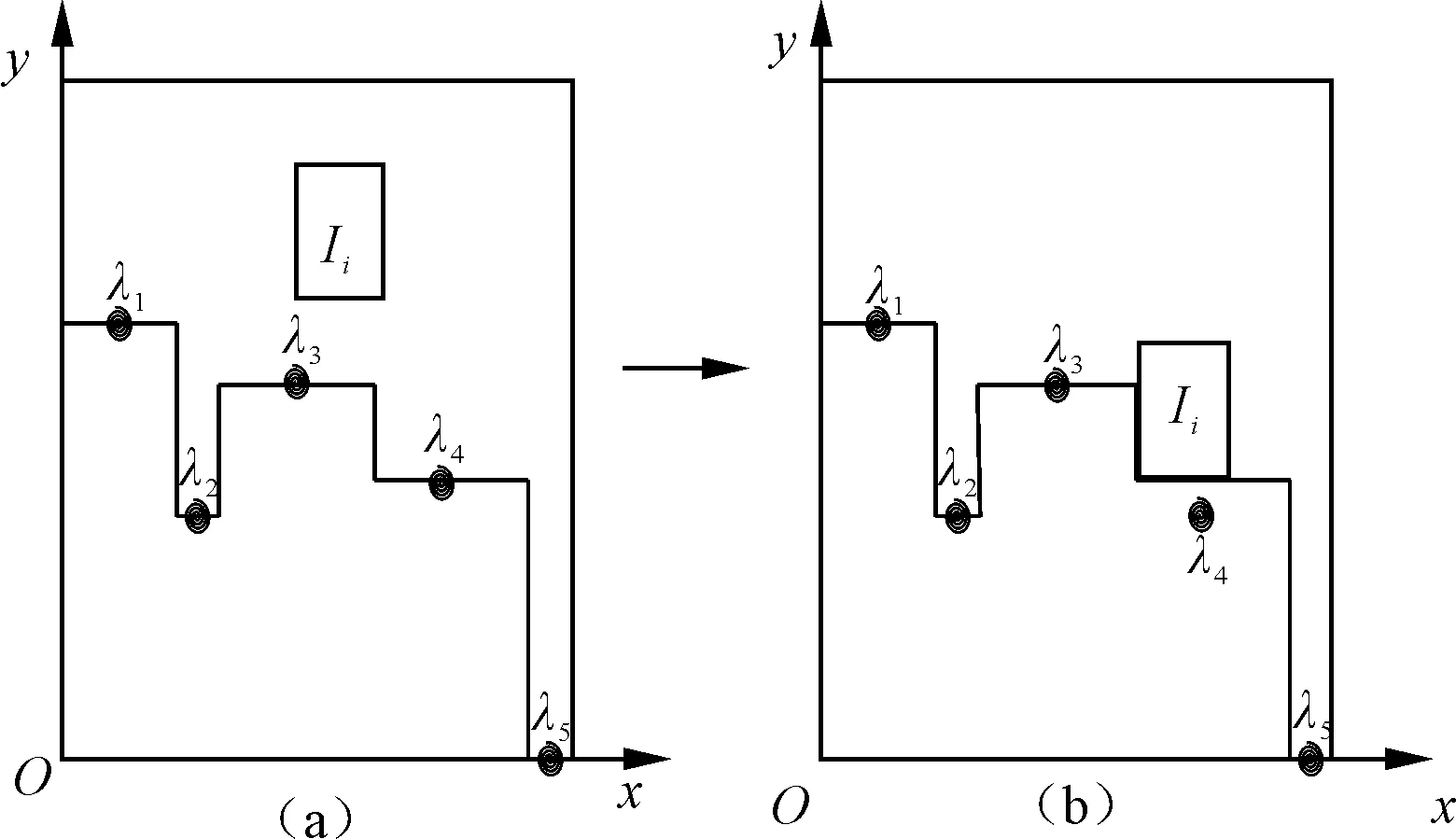
图4 车辆Ii选择适当位置图

(7)更新水平线集合，判断甲板剩余区域是否可以继续停放车辆。若可以，从其余车辆挑选合适的车辆进行配载，并重复步骤(6)；若无法继续停放其余任何车辆，则结束配载工作，生成配载方案。算法流程如图5所示。

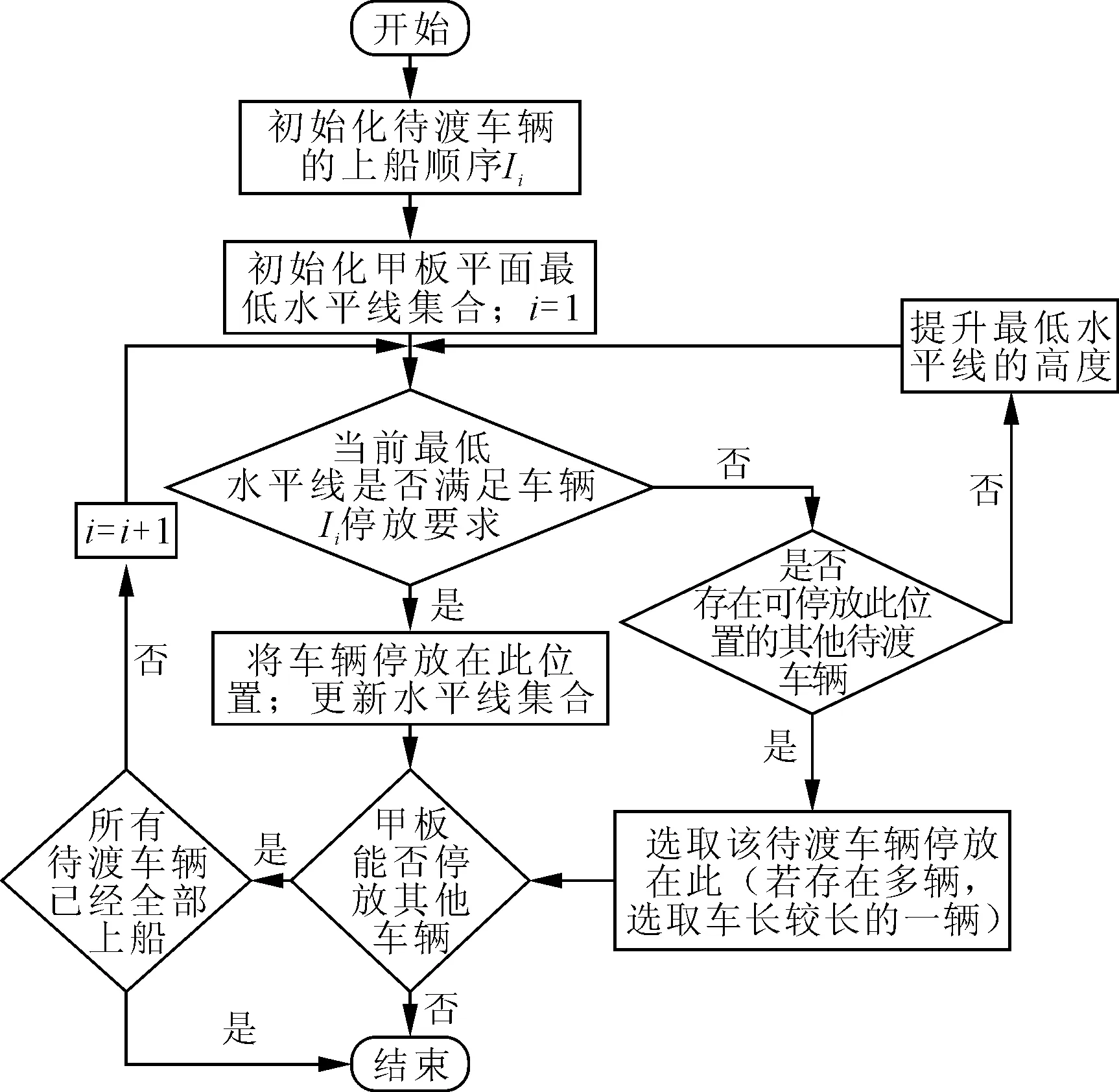
图5 最低水平线算法流程图

4 场景模拟及分析

为了验证客滚船配载优化模型和算法的有效性，分别设计一般场景和特殊场景下的仿真实验，实现客滚船配载优化决策。

4.1 一般场景优化决策

4.1.1 场景设置

根据对琼州海峡客货滚装业务进行分析，由于配载对象为社会渡海车辆，其出行规律有一定的社会属性，典型渡海车辆数据参考文献[13]，白天(D)小车较多，货车较少，少量客车；晚上(N)货车居多，小车较少，无客车。对不同时段渡海车辆的车型比例进行假设，如表1所示。车辆间的安全距离设置为0.2 m，即dx、dy的大小为0.1。典型实验客滚船船型数据如表2所示。

表1 不同时段的车型比例

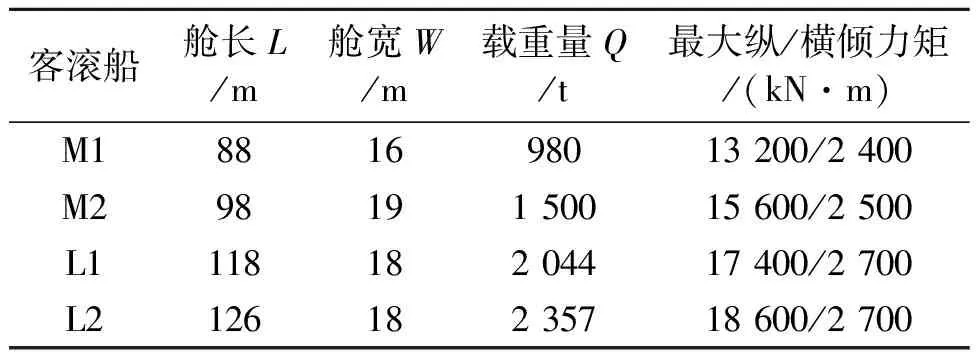
表2 典型实验客滚船船型数据

为了方便叙述，不同场景利用M/L-D/N-R的方式来表示，其中D/N表示配载业务是白天或是晚上，R表示不同情况下的各车型具体比例，M/L表示不同规格的客滚船。各类车型的渡海费用参考有关部门制定的标准：客车为560元/辆；小车为374元/辆；货车为计重计费，约合40元/t。

利用MATLAB 2019a求解构建的模型，经多次试验，将算法种群规模设置为100，迭代次数设置为200，交叉概率为0.95，变异概率为0.2，模型最大求解时间设置为120 s，为避免出现偶然性，每个场景进行10次方案输出，取其平均值。

4.1.2 决策方案

16种不同场景下的实验结果如表3所示，f表示每个场景运行10次客滚船船舱甲板可载区域利用率的平均值，f′表示每个场景下10次实验结果的标准差。

由表3可知，对于4艘不同规格的客滚船，在不同的时间、不同车辆种类及比例、不同待渡车辆规模的情况下客滚船的船舶面积利用率均达到了96%左右，标准差基本在0.005左右，证明模型算法具有良好的稳定性，求解性能良好。

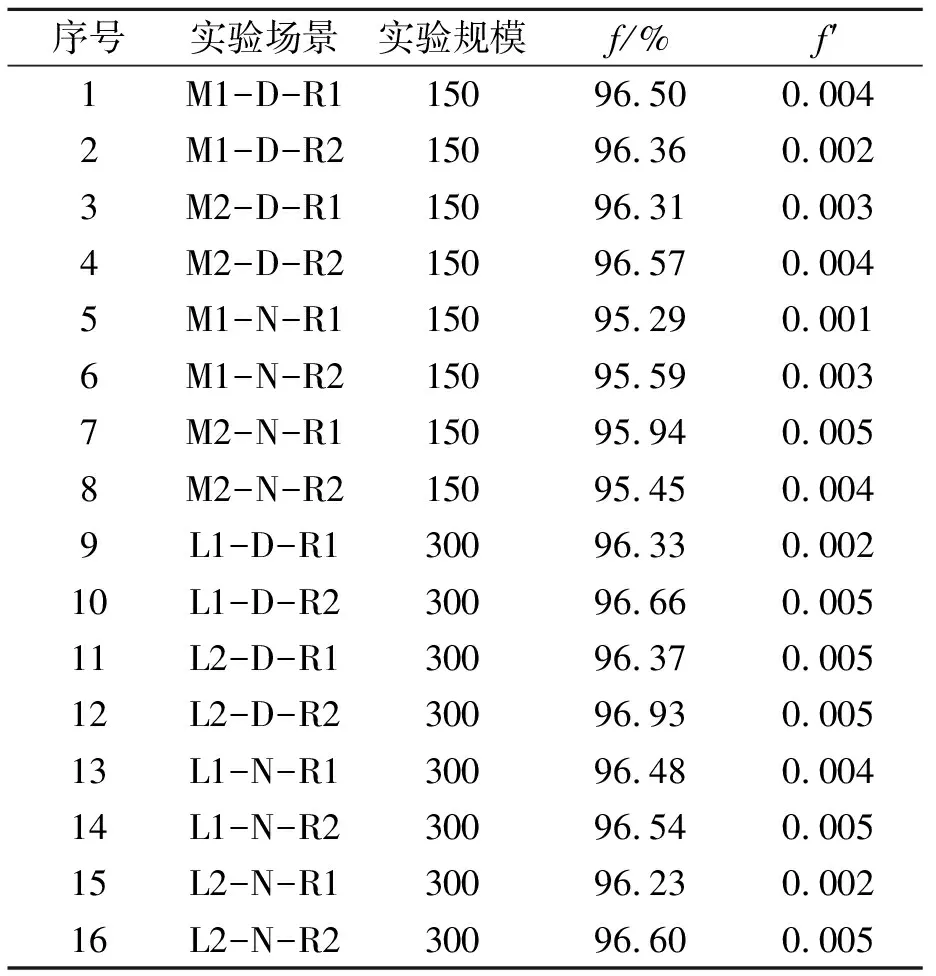
表3 不同场景下客滚船车辆配载方案

其中面积利用率在95%的场景均为小型客滚船M1、M2，由于晚间发船，小车比例少，无法填补货车产生的空隙，造成面积的小部分浪费，降低了船舶的面积利用率。而船型较大的客滚船L1、L2其面积利用率能够维持在较高水平，从侧面说明客滚船的大型化能够在车型更杂的现实作业中提高船舱甲板的利用率。

图6为场景M2-D-R1中的一次求解结果的配载可视化方案，客滚船船舱面积利用率达到了97.04%，该航次车辆总运费65 756元，车辆总重771.8 t，处于安全航行的状态，车辆中所标示的数字为车辆到达序号，矩形所在位置即车辆上船后停放的具体位置。

图6 场景M2-D-R1配载方案可视化展示

4.2 特殊场景优化决策

4.2.1 场景设置

场景一：模拟当港口受极端天气影响时，港口出现车辆积压问题，为加快港口运作效率，尽快发送车辆和旅客，为港口车辆配载工作提供可行且高效的配载方案。

场景二：模拟客滚运输业务淡季时，渡海车辆数目较少，单个航次无法满舱时，为港口车辆配载工作提供可行的配载方案。

各待渡车辆的车型以及各项参数同4.1节，客滚船舶选取目前在航线“海口—海安”营运的客滚船舶“紫荆二十二号”、“宝岛12号”两艘客滚船进行场景模拟，其参数分别为：“紫荆二十二号”的船舶总长127.5 m，型宽20.88 m，额定载货量3 150 t；“宝岛12号”的船舶总长106 m，型宽19.8 m，额定载货量1 574 t。

4.2.2 决策方案

场景一当港口出现大量待渡车辆积压在港口时，根据港口总平面布置图，此时待渡场内停放的货车、小车、客车的数量分别为260辆、160辆、60辆，利用客滚船“紫荆二十二号”进行配载作业。为了减少随机性，分别进行10次模拟实验，船舱面积利用率在97%左右，平均利用率为97.35%，标准差为0.003，说明基于模型及算法得出的优化决策能够一定程度上解决港口车辆的积压问题，以实现在短时间内有序地指挥调度车辆进行登船作业，快速发送车辆。第8次的配载方案示例如图7所示。

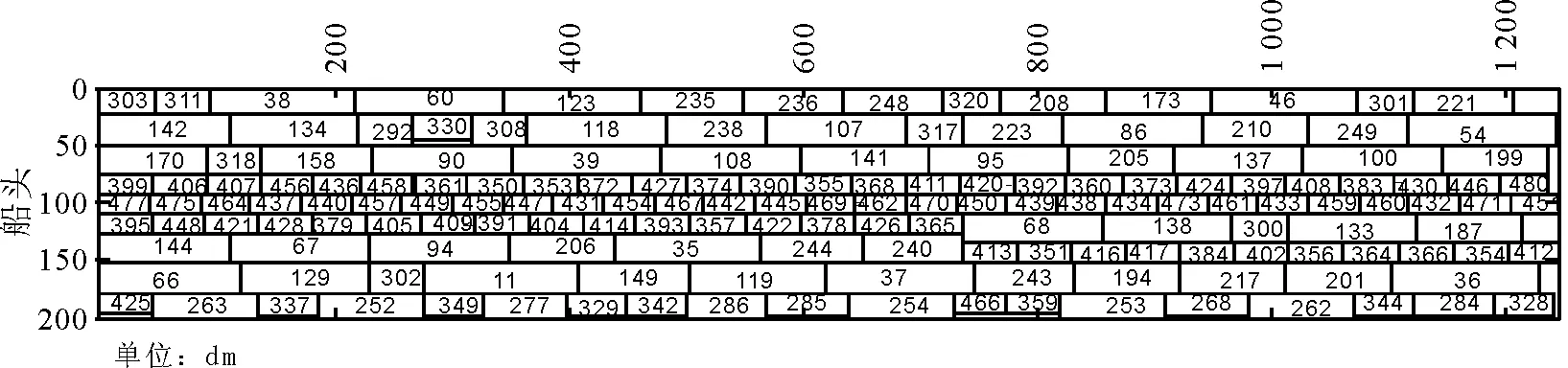
图7 第8次配载方案可视化展示

场景二为客货滚装运输业务淡季时的场景，假设仅80辆待渡车辆等待渡海，各类车型以及各项参数同4.1节，随机产生。经求解，输出该航次的一种较优配载方案，其车辆总重643.2 t，如图8所示，同种类型的渡海车辆从左至右均匀分布，保证船舶不会发生横倾的风险，从船头方向往船尾看，小车集中于在船头侧的甲板上，货车及少量的客车等大型车辆偏甲板中间停放，此时船舶纵倾约为8 190 kN·m，在最大横倾力矩范围内，能够充分保证船舶的航行安全，配载方案合理。

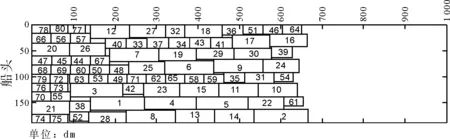
图8 淡季客滚船配载可视化展示

5 结论

笔者针对琼州海峡新海港客滚船配载决策问题：①引入矩形件排样优化理论，并结合实际，以船舱面积利用率最大为目标，构建客滚船配载优化决策模型，设计了融合基于K-邻域搜索的遗传算法和最低水平线算法的求解方案。②通过模拟在不同场景下客滚运输业务，当渡海车辆数量充足时，船舱面积利用率能够达到96%左右的较高水平；当渡海车辆数量较少时，同样能够满足实际场景中客滚船配载要求，输出合理的配载方案。③配载优化决策方法能较好地适应不同的客滚船配载场景，对于不同场景下的客滚船智能配载决策均有一定的指导意义，能够有效提升客滚运输业务的营运效率，且一定程度上能够保证港方收益。后续，将针对多层客滚船的配载以及当无法已知全部渡海车辆信息时的动态配载进行研究。