基于不同评估标准的轨道车辆吊装设备焊缝疲劳强度分析*

王得羽，李晓峰

(大连交通大学机车车辆工程学院，辽宁大连 116028)

0 引 言

牵引变压器是保证动车组正常运行的重要装备。如果在列车服役过程中，其焊缝产生疲劳断裂，将产生巨大的安全隐患。 因此，在设计阶段对其焊缝进行疲劳分析是至关重要的。 目前应用较广的焊缝评估方法为结构应力法，但由于缺少其载荷谱，所以在分析时并不考虑随机振动的影响[1]。 而列车在运行过程中会承受各种复杂的环境载荷，所以在实际工程应用中使用计算简单且精度足够的频域法随机振动对吊装进行疲劳分析。 同时，目前吊装结构的随机振动疲劳分析仅对其结构整体的最大应力值点进行分析[2-3]，而忽略焊缝的疲劳损伤分析。

笔者以某动车组牵引变压器为研究对象，分别基于EN 12663 标准[4]和IEC61373:2010 标准[5]，使用结构应力法和随机振动频域法对焊缝进行疲劳损伤分析，得出了两种牵引变压器吊装设备焊缝的抗疲劳性能结果，并对结果进行了对比分析。

1 基本原理

1.1 结构应力法

焊缝结构同焊接母材结构不同，焊缝焊趾处存在与生俱来的微小裂纹，因此其并不存在裂纹萌生阶段。 所以，可以认为焊缝的疲劳断裂过程仅是一个单纯断裂力学问题。 P.DONG[6]通过与断裂力学的理论相结合，将焊缝界面上高度非线性的应力进行分解，提取有限元结果中与外力平衡的节点力进行计算并修正后，得到等效结构应力。 之后以等效结构应力变化范围为参量，以两阶段裂纹扩展模式和断裂力学为基础，建立了基于结构应力的主S-N 曲线焊接结构疲劳寿命的理论模型。

焊缝疲劳寿命按式进行计算:

式中:N为疲劳寿命循环次数；Cd及h为曲线常数；ΔSs为等效结构应力变化范围:

式中:m为裂纹扩展参数，；t为实际板厚与单位板厚之比；I(r)为描述载荷模式效应的无量纲函数。 其中r为弯曲比:

式中:Δσm和Δσb分别是膜应力变化范围和弯曲应力变化范围。

该方法摆脱了传统名义应力法和热点应力法必须依赖固定的接头类型和加载模式以及对网格形状尺寸极度敏感的限制。 可更加精准地预测疲劳寿命。

1.2 随机振动基本原理

对于一个平稳随机振动过程x(t)，它的自相关函数定义为乘积x(t)x(t＋τ)的平均值，且自相关函数的值与绝对时间t无关，仅为时间差τ的函数，描述了随机振动过程中时域特性[7]，表达式如下:

式中:T为振动的周期。

Sx(ω)为随机过程的自功率谱密度，是圆频率ω的函数，描述了随机振动过程中频域特性，表达式如下:

同时，可通过对自功率谱密度函数Sx(ω)进行傅里叶变换得到自相关函数Rx(τ)，通常将式(5)、(6)叫做韦纳-辛钦定理。

理论中，Sx(ω)定义为双边谱密度，但是在工程实际中频率ω＞0，通常利用其偶函数的性质，得到单边谱密度Gx(ω):

2 结构应力法焊缝疲劳分析

2.1 有限元模型及焊缝选取

文中以某动车组牵引变压器为研究对象，材料应用Q345 钢，建立有限元网格模型，结构整体及焊缝均采用壳单元建模，有限元模型如图1 所示，有限元模型单元总数为48 136，节点总数为47 504。 此次计算共定义6 条焊缝、12 条焊线。 基于结构有限元分析结果及以往焊缝疲劳分析经验，文中仅选取1 条焊缝、2 条焊线进行疲劳损伤分析。

图1 有限元模型

2.2 结构应力法疲劳分析

根据标准EN 12663 中相关规定，牵引变压器属于P-Ⅰ类车辆车下设备，选取疲劳工况如表1 所列。为方便计算，总循环次数选取1 000 万次。

表1 疲劳工况

使用自主研发的焊接结构疲劳寿命分析软件Weld Fatigue 对选取的关键焊缝进行疲劳损伤分析。首先，使用ANSYS 软件对模型进行整体疲劳工况计算；然后，使用Weld Fatigue 对关键焊缝进行各工况等效结构应力的计算；最后，根据计算结果选用可靠度为97.7%的-2σ主S-N 曲线，计算得出每一工况下的疲劳损伤比Di，叠加得出总损伤比D。 计算结果如图2～3 所示。

图2 焊缝疲劳寿命云图

分析计算结果，最大损伤比节点位于关键焊缝焊线1 起始位置，此节点疲劳损伤比小于1，故不会发生疲劳破坏。 其余位置损伤比数值极小可忽略不计。综上，通过结构应力法分析，此关键焊缝在三个工况下均不会发生疲劳破坏。

但是，车辆在服役过程中会承受各种复杂的随机载荷，此焊缝位于悬臂结构与主结构交界处，属于结构突变位置，如果受到随机振动影响，必然会对此焊缝的疲劳强度造成进一步削弱。 因此，为验证关键焊缝的可靠性，需对此结构进行随机振动分析。

图3 焊缝计算结果

3 随机振动疲劳分析

3.1 载荷谱选取

根据IEC 61373-2010 标准规定，牵引变压器直接受到车体底架激励，且其自重大于1 250 kg，属于Ⅰ类-A 类车体吊装设备，选取垂、横、纵三个方向加速度功率谱，如图4 所示，关键点坐标值如表2 。

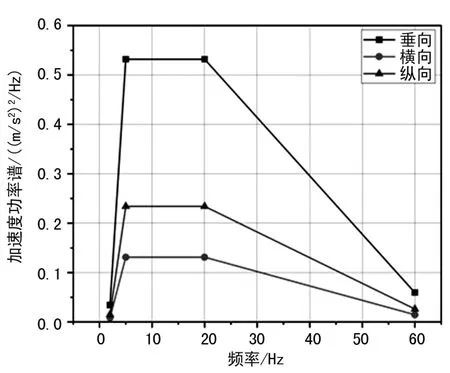
图4 加速度功率谱

表2 各向加速度功率谱值

3.2 模态分析

根据IEC 61373:2010 标准规定，计算模态频率范围应大于功率谱密度频率范围的3/2，故进行前30阶模态计算，扩展模态选取30 阶。 计算时应用ANSYS 软件采用Block Lanczos 法进行有约束模态分析，约束位置选取牵引变压器与车体底架螺栓连接位置。分析结果如表3 所列。

表3 前三十阶模态频率

3.3 随机振动疲劳寿命分析

随机振动计算时，激励点选取模态分析过程中的约束位置。

对模型施加的各方向激励进行功率谱分析，分析完成后进行模态合并，得到结构总体响应。 在分析结果中选取1σ 应力结果显示，对关键焊缝三个方向激励产生的响应结果进行分析，关键焊缝最大1σ 应力云图如图5 所示。

图5 焊缝各工况1σ 应力云图

分析发现最大1σ 应力发生在纵向激励工况，为34.296 7 MPa，因篇幅限制，文中仅对其纵向激励工况进行疲劳寿命分析。

利用高斯三区间法[8]对随机振动疲劳进行分析。 为与之前结构应力法疲劳分析结果进行对比，此次各方向总循环次数N选择为1 000 万次。 计算出1σ、2σ、3σ 水平下的循环次数为n1σ、n2σ、n3σ:

式中:v＋为平均振动频率。

提取焊线1、2 中各节点1σ 应力，并计算出2σ应力和3σ 应力。 根据BS 7608: 2014＋A1: 2015 标准[9]，确定焊缝类型为F2 级，具体参数见表4，并进行各节点不同应力水平的疲劳损伤计算。 各节点不同应力水平疲劳损伤结果通过Miner 累积损伤理论叠加，得出关键焊缝各节点总损伤比，如图6 。

图6 关键焊缝纵向工况各节点总损伤比

表4 F2 级焊缝参数

可以明显看出，关键焊缝出现多结点疲劳损伤比大于1 的情况，也就是说此焊缝并不满足疲劳寿命的设计要求，并将在焊缝起始和末尾发生断裂。

文中以疲劳损伤比最大节点48 633 为例，对其纵向工况进行分析。 提取其位移、速度、加速度响应谱，如图7。

图7 节点48 633 纵向响应谱

通过分析响应谱，可以观察到，节点48 633 的位移、速度、加速度响应在24 ～25 Hz 频率附近出现峰值。 对比结构有约束模态，发现该频率与其第4 阶模态频率相重合，导致结构在24.6 Hz 附近发生共振，其模态振型如图8 所示。 焊缝位于悬臂结构与主体结构交界处， 在此阶振型中，结构在焊缝垂直方向发生相对位移的，导致关键焊缝疲劳损伤增大。

图8 第4 阶模态纵向位移云图

4 结 论

文中基于EN 12663 标准和IEC61373:2010 标准分别对某动车组牵引变压器应用了结构应力法和随机振动频域法对其焊缝疲劳损伤进行计算，并对两方法的计算结果进行了对比分析，可以得到以下结论。

(1) 在计算焊缝疲劳时，工程实际中一般使用基于EN 12663 标准的结构应力法。 但由于此标准输入载荷并不考虑随机振动的情况，此方法无法准确地描述出吊装设备结构共振对疲劳损伤的影响。

(2) 在计算轨道车辆吊装设备疲劳时，一般使用基于IEC61373:2010 标准的随机振动频域法分析，且分析过程中仅对整体的1σ 应力值最大点进行评估，忽略焊缝的疲劳损伤评估。 本次计算结果表明，当1σ 应力值最大点不发生在焊缝处时，焊缝依旧会发生疲劳断裂。 故在车下吊装设备疲劳分析时，应考虑其焊缝的疲劳强度问题。

(3) 在实际工程应用中，对吊装设备焊缝进行疲劳评估时，应先对其进行基于EN 12663 标准的结构

应力法的疲劳评估。 再判断其主要振动频率是否落入复杂载荷激励频谱区间，若在频域内，则需再对其先进行基于IEC61373:2010 标准的随机振动疲劳分析。