基于随机三层环形子电路的路径级NBTI老化预测

徐辉，朱瑞，孙侠，何富贵

（1.安徽理工大学 计算机科学与工程学院，安徽 淮南 232001；2.安徽理工大学 数学与大数据学院，安徽 淮南 232001；3.皖西学院 电子与信息工程学院，安徽 六安 237012）

随着CMOS 器件尺寸的不断缩小，芯片的集成度越来越高[1-2]，晶体管的特性也发生了很大的变化，这给电路的可靠性带来了巨大挑战[3]。导致CMOS 电路可靠性的原因有很多，包括负偏置温度不稳定效应（Negative bias temperature instability，NBTI）、热载流子效应（Hot-carrier injection，HCI）[4]，它们会影响晶体管的电气特性，并导致电路时序紊乱，甚至引起电路功能失效[5]。研究结果表明，当电路经受的NBTI 超过10 年时，电路的老化时延最大可以增加20%[6]。

目前，国内外针对NBTI 的解决方法主要包括门替换[7-8]、输入向量控制[9]、插入传输门[10]，但是这些方法需要我们预测电路关键路径的老化延时，从而在设计阶段减少NBTI 效应带来的影响。对于电路关键路径老化延时的研究主要分为以下几类：第一类使用HSPICE 仿真工具从晶体管级来模拟整个电路[11]，它得到的精度是目前最高的，但是模型处理时间也是最慢的；第二类使用基于查找表（Look-up table，LUT）的模型[12]，虽然模型处理速度提升了，但精度相比于传统的HSPICE 却降低了；最后一类使用机器学习[13-15]，其精度较高，但模型处理时间有待提高。

为了快速得到关键路径老化延时同时实现高精度，本文提出了一种基于随机三层环形子电路的路径级老化预测模型。电路是由不同的门组成的，在不考虑电路中线的老化延时的情况下，其关键路径的老化延时就是门老化延时在电路中的宏观体现。随机选取若干三层环形子电路，通过实验，发现它们的老化延时趋势和电路关键路径的老化延时趋势具有高度的相似性。将得到的这些三层环形子电路的老化延时数据作为训练集，训练集的输入是三层环形子电路的第0 年和第1 年的老化延时数据，输出是三层环形子电路的第2 年至第10 年的老化延时数据。基于训练之后的模型，当获得关键路径少量已知老化延时数据，即关键路径第0 年和第一年老化延时数据，就能推断出该关键路径其余时段的未知老化延时数据。相比于其他的机器学习方法，本文的模型在速度上有明显提升，同时由于三层环形子电路与关键路径之间的联系，保证了预测精度。

1 背景知识

1.1 基于NBTI 的老化预测模型

当PMOS 管的栅极输入信号始终是0 时，该晶体管遭受的是静态NBTI 的影响；当该PMOS 管栅极输入信号交替的为0 和1 时，该晶体管承受动态NBTI 的影响[7]。在一个集成电路的正常生命周期内，受不同工作状态的影响，该电路经受的动态NBTI 和静态NBTI 所产生的老化效应也不同。考虑上述情况，一个长期的针对NBTI 的老化预测模型[10]：

式中，a为占空比，也称为负载周期，是指周期信号中低电平所占的比例；Kv为与温度和电源电压相关的参数；Tclk为时钟周期；n为扩散常数，当栅极聚集的H+以原子形式扩散时，n取值1/4，以H2形式扩散时，n取值1/6；tβ与温度、占空比、时间和工艺参数有关。通过该式可以看出，PMOS 晶体管管阈值电压的变化量主要受占空比，时间，以及温度的影响。基于该老化模型，在NBTI 影响下，经过t时间门的传播延时增量ΔtD可以近似为[10]

式中，B为由门的类型和制造工艺决定的常数，通过HSPICE 仿真数据拟合得到。

对于输入信号的一些参数，例如频率、占空比，都是在某一个区间里离散的取值，并不是连续的取值。所以可以去遍历某一个门电路的所有参数，使用式(2)计算出退化前后的延迟。把所有的延时退化情况统计在一张多维表格中，这样对于后面的电路仿真，只需要查表就可以得到电路具体的退化情况[12]。

1.2 获取关键路径

本文使用了一种静态时序分析方法（STA）来获得关键路径集合，如图1 所示。首先对DC 综合后的门级电路网表文件通过拓扑排序算法建立有向图结构，之后利用STA 得到电路每个路径老化前的延时Ts与电路最长路径的延时Tmax，设置时序余量cT和电路的老化上限 Aginemax， Aginemax采用MDS（将电路中所有节点的占空比设置为0.95），则满足式(3)的路径均被作为电路潜在关键路径（potential critical paths set，PCP）。再使用基于NBTI 的回溯算法求取PCP 集合中所有路径十年内的老化延时dT，满足式(4)的路径加入关键路径集合。

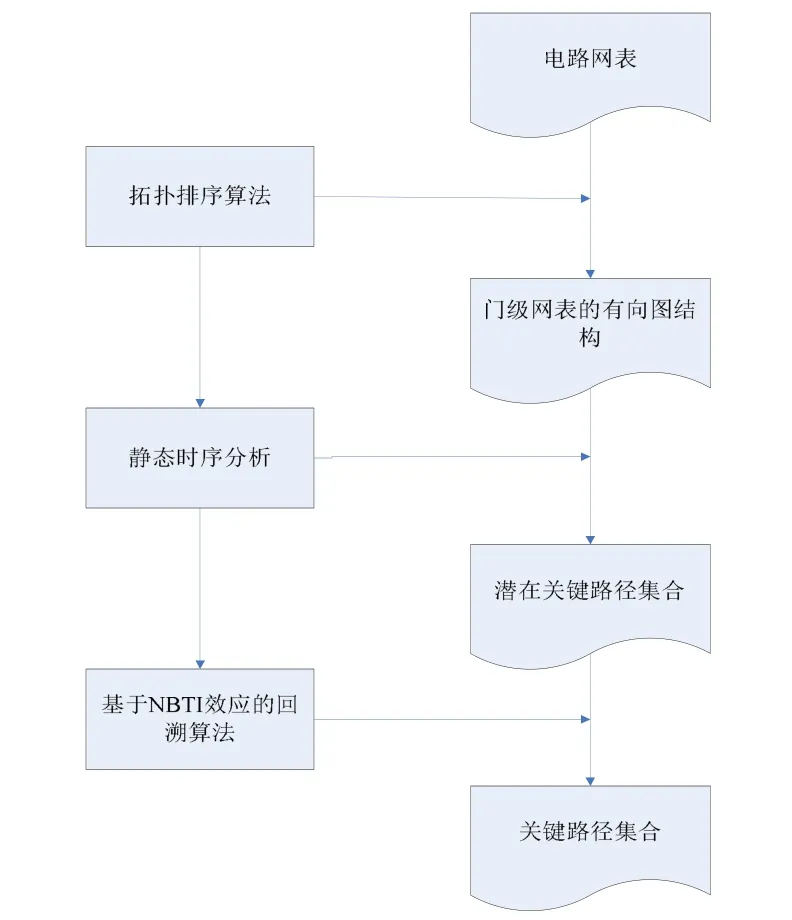
图1 获取关键路径流程图

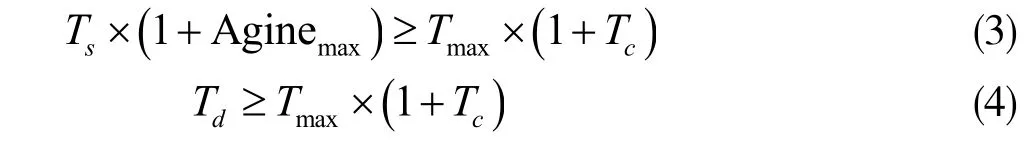
2 方法

2.1 建立三层环形子电路

电路的有向图表示为G=（v,e），V= {vi,1≤i≤n}作为节点的集合，代表电路中的门；E= {ej,1≤j≤m}作为边的集合，代表门与门之间的连线。首先建立初始集合TiO，将iv加入TiO，将iv的前驱节点和后继节点加入集合TiO和集合TO1i，TO1i称为iv的一层拓扑环。接着将TO1i中每个节点的前驱节点和后继节点，且这些节点不包括在TO1i中，加入TOi和TO2i，TO2i称为vi的二层拓扑环，以此类推，TO3i称为vi的三层拓扑环，最终得到的TiO即为三层环形子电路。如图2 所示为2-C17 电路G7 的一层、二层、三层环形子电路。从图2 中可以看到，在建立G7 的三层环形子电路的过程中，形成了以G7 为顶点，指向它的前驱节点和它指向的后继节点延伸的树结构，分别称它们为前驱区域和后继区域。

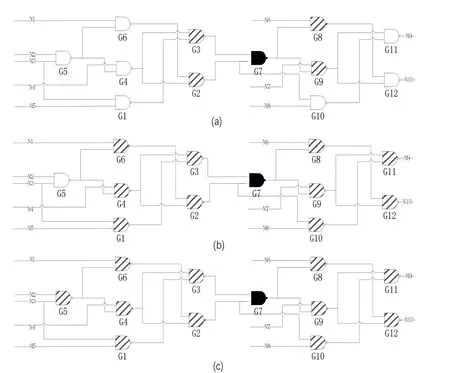
图2 2-C17 电路G7 (a)一层环形子电路 (b)二层环形子电路 (c)三层环形子电路

三层环形子电路老化延时算法需要使用HSPICE 仿真iv在不同状态下的延时，它们的老化延时都是基于特定的条件下计算的。以iv作为顶点，使用深度搜索算法（DFS）分别计算其前驱区域和后继区域的最长老化延时，三层环形子电路的老化延时就是这两个区域老化延时的累加。假设随机门的数量是r，DFS的时间复杂度为O(v)，算法的复杂度为O(r.v)。

2.2 线性回归模型

线性回归是一种对一个或多个自变量和因变量之间关系进行预测的模型。线性回归算法是由线性叠加函数表示决策函数，利用最小化损失函数得到对训练集样本而言最好的模型，这样对于新样本的数据，可以通过建立的模型进行分析预测。线性回归算法的模型为

其中，x是因变量，y是自变量，w和b是模型参数。

本文调用sklearn 库里面的线性回归模型进行训练，三层环形子电路的老化延时数据作为训练集U，U包括n条三层环形子电路的第0 年到第10 年的老化延时数据，时间步长为1 年。由于是利用关键路径的第0 年和第 1 年的老化延时数据来获得该关键路径的其余老化延时数据，所以将U分为二类：Uin= {,0 ≤p≤ 1,1≤a≤n}，代表着中Uin第a个三层环形子电路第0 年和第1 年的老化延时数据，作为线性回归模型训练集的输入数据；Uout= {,2 ≤q≤ 10,1≤a≤n}，代表Uin中第a个三层环形子电路第2年至第10 年的老化延时数据。综上，U的输入集Uin、输出集Uout如下：

电路关键路径延时数据作为测试集，K包括m条关键路径的第0 年到第10 年的老化延时数据，时间步长为1 年。同理，将K分为二类：Kin= {,0 ≤p≤ 1,1≤b≤m}代表Uin第b条关键路径第0 年和第1 年的老化延时数据，作为线性回归模型测试集的输入数据；Kout= {,2 ≤p≤ 10,1≤b≤m}，代表Kout中第b个条关键路径第2 年至第10 年的老化延时数据，作为线性回归模型测试集的输出数据。综上，K的输入集Kin和输出集Kout如下:

本文求取了c2670 基准电路中三层环形子电路U= {u_i, 1 ≤i≤5}第0～10 年的老化延时（单位为ps），步长为1 年；关键路径K= {k_j, 0 ≤j≤1}第0～1 年的老化延时，如表1 所示。根据之前的定义，只要得到p_1 第0～1 年的老化数据，通过我们的模型，那么就能获得其第2 年到第10 年的老化数据，即表格中的“-“所包括的区域。

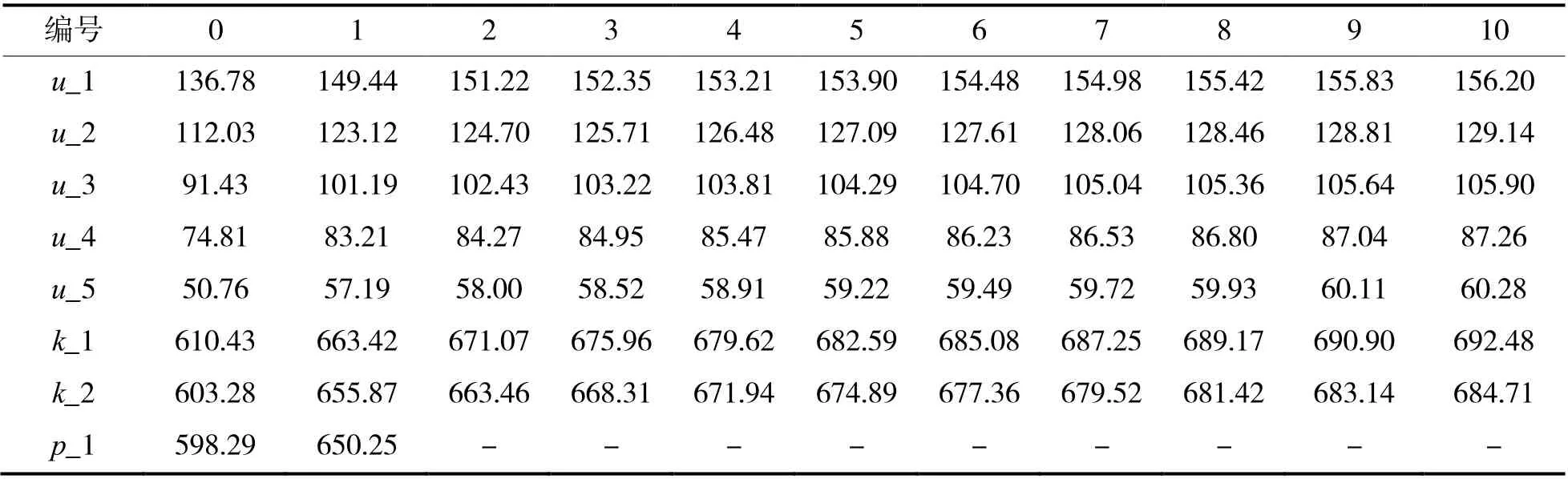
表1 c2670 基准电路随机三层环形子电路和关键路径老化延时数据

通过线性回归模型训练U的Uin和Uout得到模型ML，这样对于Kin中的，就能使用ML 模型得到预测的，机器学习模型如下：

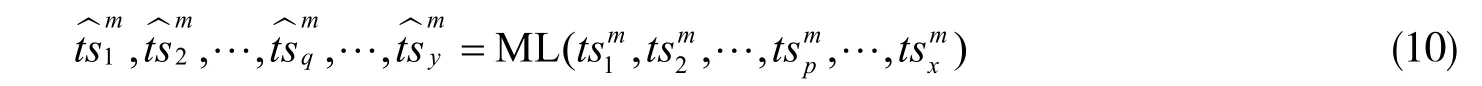
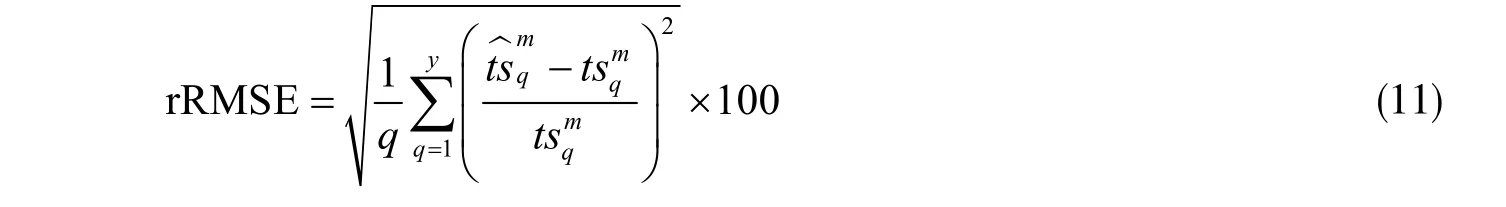
2.3 建立老化预测框架

本文设计的老化预测框架如图3 所示，首先综合原始基准电路的网表文件并采用深度优先搜索算法来对电路进行拓扑排序。之后，结合工艺参数和NBTI 老化模型参数信息，建立整个电路的有向图结构。基于该有向图，结合温度、占空比等老化影响参数，分别使用三层环形子电路老化延时算法和STA 求出三层环形子电路延时和部分关键路径在不同老化年限下的延时，得到的三层环形子电路老化延数据作为训练集，部分关键路径老化延时数据作为测试集。最后，通过线性回归模型模拟子电路的老化趋势并基于该模型预测其余的关键路径老化延时。

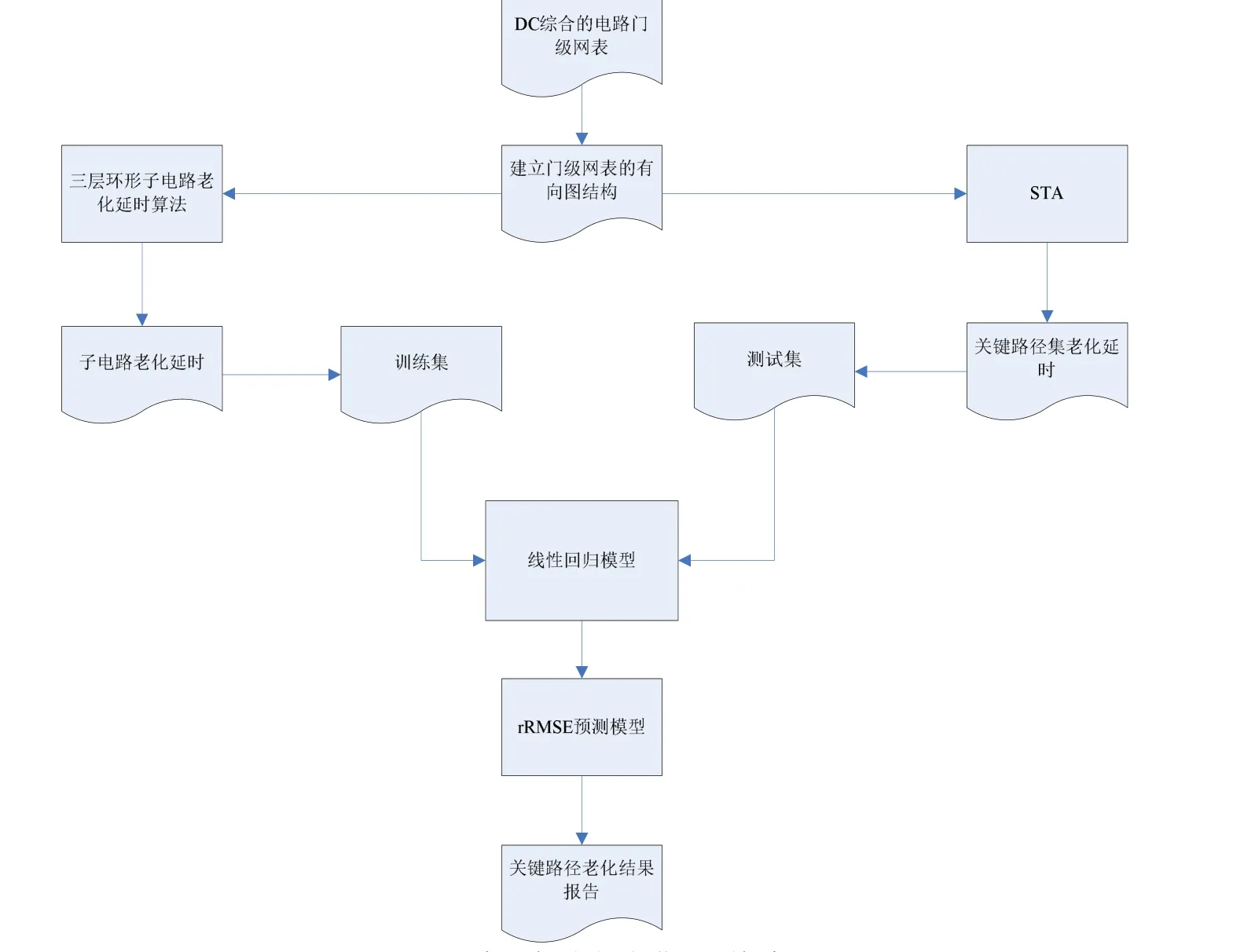
图3 本文提出的老化预测框架

3 实验结果及分析

为了论证本文提出的模型，选用了ISCAS'85、ISCAS'89 基准电路进行验证，所使用的实验电路经过Synopsys 公司的Design Compiler 综合工具基于PTM32nm 晶体管模型综合的。在综合过程中，网表由INV、2-4 输入的NAND 及2-4 输入的NOR 基本逻辑门单元组成。使用HSPICE 仿真这些门在不同状态下的延时。使用2.2 节的方法获取关键路径，时序余量Tc= 10%，和电路的老化上限 Aginemax=20%，并计算其10 年的老化延时，时间步长为1 年，模型采用C++编译，运行在Visual Studio 2019。随机三层环形子电路的选取通过Python 里NumPy 中的random 模块来实现。由于老化延时受到操作条件的影响，将操作条件设置为：O=[a,T]，a代表考虑不同负载下主输入X%在每个时钟周期中为“1”的概率，即占空比，a取1%，25%，50%，75%，99%。T代表电路工作的环境温度，取25℃，50℃，75℃。

3.1 实验验证

本文选择了s9234 基准电路来验证本文的想法，实验条件设置为a=50%，T=50 ℃，实验模拟结果如图4 所示。图中的实线代表随机三层环形子电路的老化延时，虚线代表电路关键路径的老化延时。横轴表示电路的老化时间，包括时间t=0 ，即未老化的延时数据，纵轴表示对应时间的老化延迟。可以观察到随机三层环形子电路和关键路径老化延时趋势具有相似性，通过建立三层环形子电路的预测模型，这样对于新的关键路径，就可以使用少量已知的关键路径老化延时数据得到其余未知的老化延时数据。

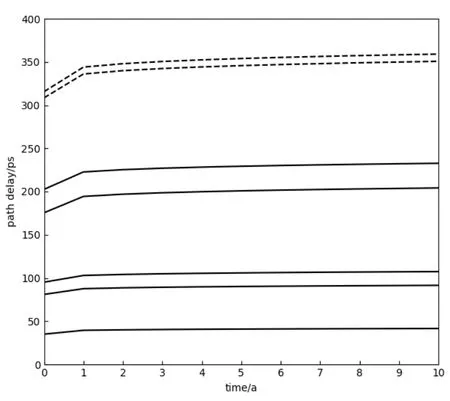
图4 s9234 基准电路的随机三层环形子电路和关键路径的老化延时趋势图

3.2 不同操作条件下的老化预测

为了评估在不同实验条件下模型的准确性，本文考虑了两种操作条件，即O=[a,T]，a取1%，25%，50%，75%，99%，T取25 ℃，50 ℃，75 ℃。关键路径老化延时将作为我们模型的比较值，rRMSE 作为评估模型精度的可靠指标。以第0～1 年的关键路径老化延时数据作为初始值，第2～10 年的关键路径老化延时作为预测值，1 年为步长。图5 是s5378 电路T= 50 ℃在，a分别为1%，25%，50%，75%，99%下其中一条关键路径实际值和预测值的散点图，实际值在x轴上，预测值在y轴上，可以观察到散点都在斜线（45°）附近，所提出的模型可以准确的预测电路的老化。表2 是不同基准电路在T=50 ℃，a分别为1%，25%，50%，75%，99%下，实验进行了1 000 次，通过随机三层环形子电路预测一条关键路径的平均rRMSE，可以看出平均rRMSE 是保持在1%左右。

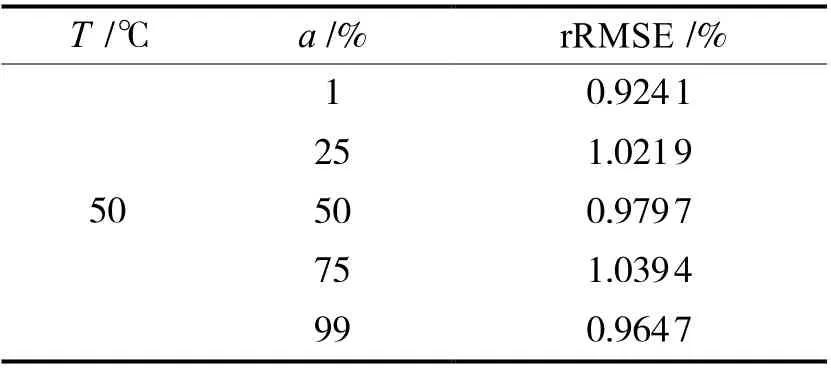
表2 s5378 电路在T= 50 ℃，不同a 下的rRMSE

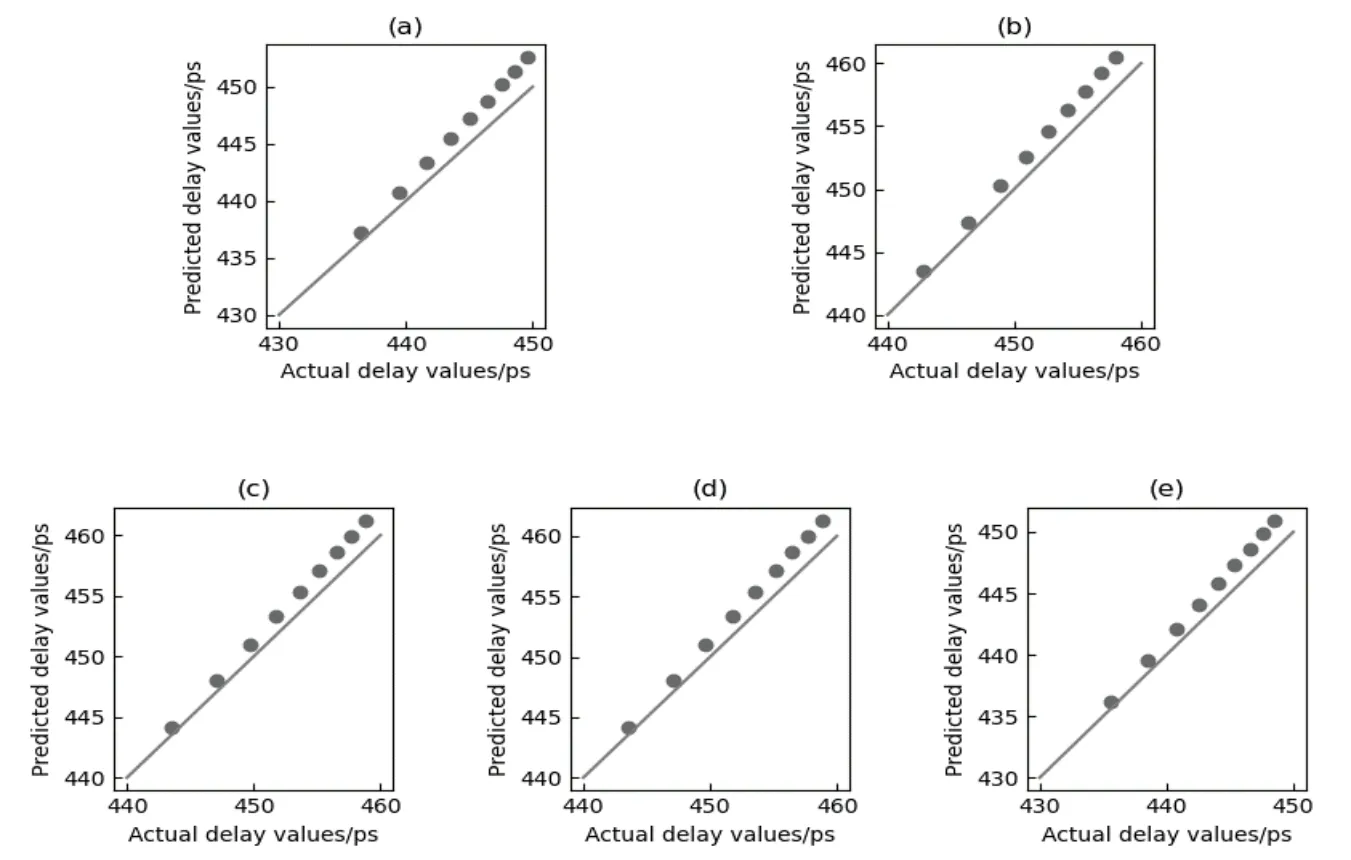
图5 s5378 电路在 T= 50 ℃的模型预测值与实际值比较 (a)a=1% (b)a=25%(c)a=50%(d)a=75% (e)a=99%

为了验证模型在不同的温度下依然具有较高的精度，本文考虑了a=50%，T分别取25 ℃，50 ℃，75 ℃。以第0～1 年的关键路径老化延时数据作为初始值，第2～10 年的关键路径老化延时作为预测值，1 年为步长。图6 是s5378 电路在该条件下随机一条关键路径预测值和实际值的散点图，可以观察到即便在不同的温度下的模型也可以准确地预测电路的老化。表3 是不同基准电路在a=50%，T分别取25 ℃，50 ℃，75 ℃下，进行了1 000 次实验，通过随机三层环形子电路预测一条关键路径的平均rRMSE，对于不同温度下的老化预测，本文的rRMSE 保持在1%左右。

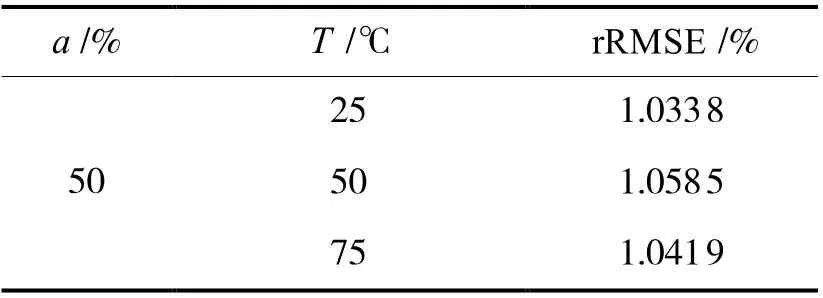
表3 s5378 电路在a=50%，不同T 下的rRMSE

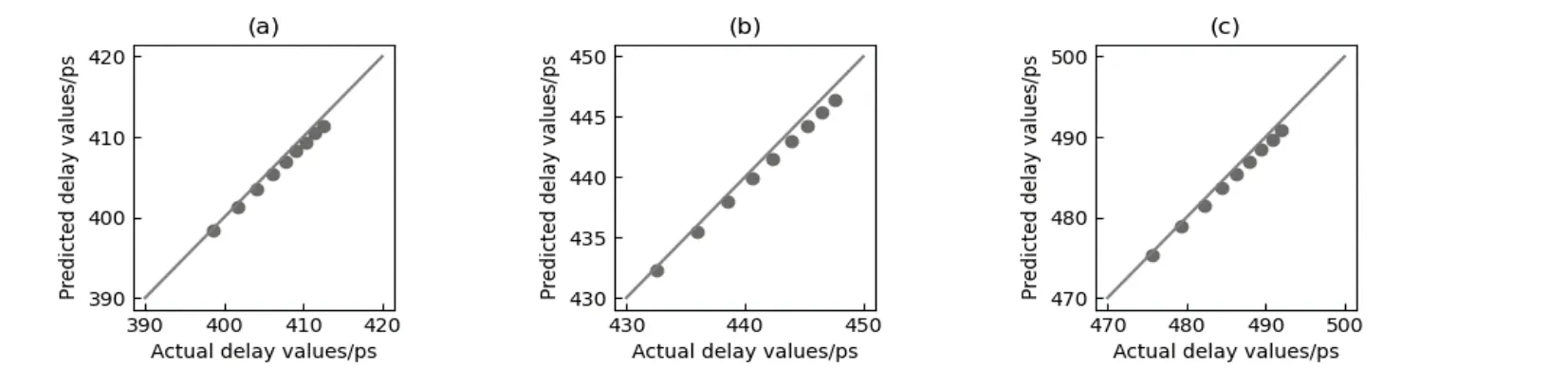
图6 s5378 电路在a=50%的模型预测值与实际值比较 (a)T=25 ℃ (b)T=50 ℃ (c)T =75 ℃

3.3 实验对比分析

为了证明提出的模型相比于其他模型具有更好的准确性，与文献[15]进行了对比。文献[15]中预测电路的老化延时是通过获取关键路径的老化延时趋势来预测其他的关键路径老化延时，相比于以往的LUT 方法，它在精度和运行时间上都有了很好地提升。表4 中的第1 列是从ISCAS'85、ISCAS'89 中选择的基准电路，第2 列是使用本文提出模型在O= [a= 50%,T= 50℃]下进行1 000 次实验得到的最坏rRMSE，第3 列是模型平均获取随机三层环形子电路所需要的时间；第4 列是文献[15]在O= [a= 50%,T= 50℃]下进行1 000 次实验得到的最坏rRMSE，第5 列是文献[15]得到关键路径所需要的时间。可以看出，与文献[15]对比，本文提出的模型在最坏rRMSE 上普遍高于文献[15]，但在时间复杂度上减小了一个数量级，同时随着电路的规模增大，时间复杂度的减小会更加明显。

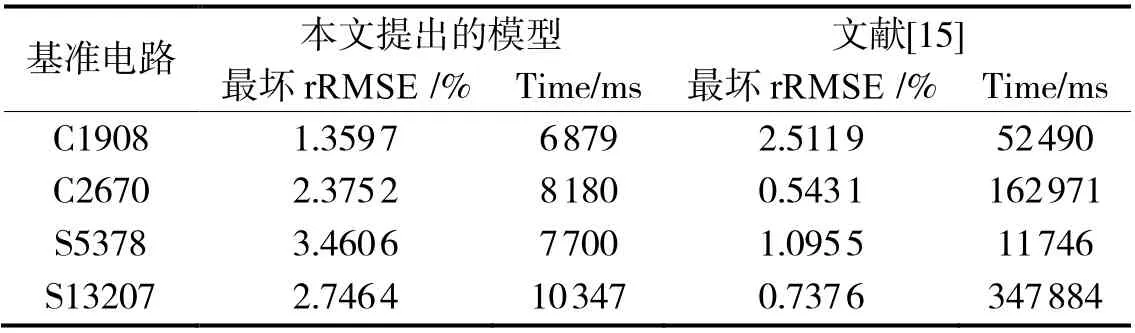
表4 不同基准电路下本文的模型与文献[15]实验结果对比

4 结束语

本文提出了一个基于随机三层环形子电路的路径级老化预测模型，用来预测NBTI 效应给电路带来的老化延时影响。通过计算三层环形子电路的老化延时趋势来预测关键路径的老化延时，虽然在较小的时间内就能得到电路关键路径老化数据，但是最坏rRMSE 与其他模型相比并没有优势，所以下一步在时间复杂度不增加的情况下，同时能够降低其最坏rRMSE 是我们主要的研究方向。