基于改进的Keller-Miksis模型的超声空化气泡动力学研究

贾蕙竹，丁婷

中北大学 信息与通信工程学院 生物医学成像与影像大数据山西省重点实验室，山西 太原 030051

引言

超声空化是液体中的微小气泡在声波作用下形成、发展和崩溃的一系列动力学过程[1]。在空化泡的溃灭过程中会产生瞬时的高温和高压，并且伴随有声致发光、冲击波、高速射流等现象[2-3]。空化效应是诸多超声治疗[4-6]过程中的关键作用机制。高强度聚焦超声治疗[7-10]是利用超声波可以穿透软组织并可以聚焦的物理特性，将超声波聚焦于体内肿瘤病灶，在焦点处形成高能密度区，使组织出现凝固性坏死，通过热效应、空化效应和机械效应等达到治疗效果，其中空化效应一方面由于声遮挡会造成损伤前移，从而影响治疗的精确性和安全性，另一方面空化泡的非线性能极大地提高机械能转化为热能的效率，从而增强热效应，提高治疗效率。在超声波溶栓[11]、超声波碎石[12]、声致穿孔[13]和组织损毁术[14-16]等超声治疗过程中，为达到较好的治疗效果，需要维持强烈的、持续性的空化作用。因此研究空化气泡在不同参数下的动力学行为有重要意义，这也是能够选择性地增强或抑制空化效应的前提条件，并为规划和监控超声治疗过程以实现精准高效的超声治疗提供理论依据。

Rayleigh[17]在1917年最早给出了无限大不可压缩液体中单个自由微泡的振动模型，但是忽略了液体黏滞性等因素的影响。在Rayleigh的基础上，Plesset[18]、Noltingk等[19]相关研究在考虑了液体黏滞性、液体表面张力后对其进行了修正，得到声场-微泡关系最常用的Rayleigh-Plesset模型，也称为RPNNP模型。该模型描述了在不可压缩液体中单个自由微泡的动力学行为，但上述模型忽略了液体的可压缩性，在大多数微泡低幅度振动的情况下是适用的，但不适用于微泡大幅度振动情况。

1941年，Herring[20]在考虑了液体的可压缩性与声场辐射后对RPNNP模型进行了优化，对能量变化进行了更好的描述。Gilmore[21]在应用Kirkwood-Bethe后也对Rayleigh-Plesset模型进行了修改，称为Gilmore模型，该方程适用于剧烈的微泡振动，如空化的产生、声致发光现象等。1980年，Keller等[22]同时考虑声辐射效应、液体黏性、微泡表面张力、液体可压缩性以及入射声波的影响，推导出了Keller-Miksis模型，该方程适用性更广。然而，Keller-Miksis方程忽略了微泡在压缩到较小半径时不能无限压缩的事实。

本文基于Keller-Miksis模型，充分考虑了传热模式对空化泡振动特性的影响以及气体不可无限压缩的事实，旨在构建一个改进的液体中单泡超声空化动力学仿真模型，该模型可描述更接近实际情况下的声场中气泡壁运动，并通过对超声场作用下液体中空化气泡的运动进行数值模拟，分析不同传热模式、空化气泡参数、液体参数和声场参数下的超声空化泡动力学行为，以期揭示超声空化瞬态物理过程，并为控制和利用空化以实现高效精准的超声治疗提供理论参考。

1 方法

1.1 Keller-Miksis模型

对于单个超声空化气泡振动模型，首先假设空化气泡内气体为空气，其满足理想气体状态方程，并且空气密度不变。空化气泡在振动过程中始终保持均匀对称的球形，假设空化气泡外液体为水，不仅需考虑微泡内蒸汽压力、液体粘滞性以及微泡表面张力的影响，同时还需考虑液体的可压缩性、声辐射效应以及入射声场的影响，得到Keller-Miksis方程[23]如公式（1）所示。

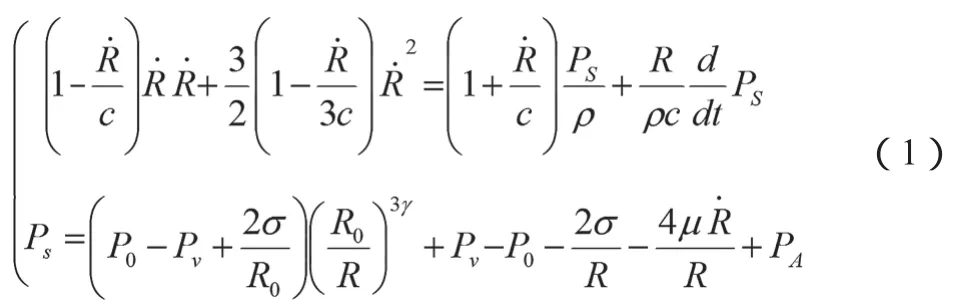
1.2 改进的Keller-Miksis模型

考虑不同传热模式影响，可将超声空化气泡振动方程表达式修正如公式（2）所示。

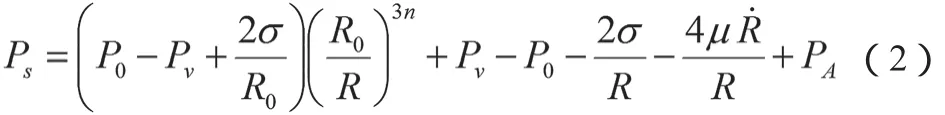
式中，n为气体的多方指数，反映过程热力学状态，取值范围是1≤n≤γ；n=1表明是等温过程，n=γ表明是绝热过程；1＜n＜γ表明是等温-绝热过程。空化气泡从生长到开始压缩的一段时间里，气泡壁的运动速度比较缓慢，此时认为空化气泡振动过程为等温过程，进而得到公式（3）。

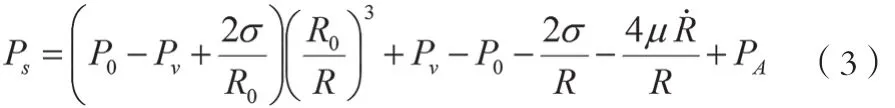
空化气泡开始压缩到比最小半径小时，一般认为此后的过程是绝热过程，考虑实际气体并不是无限压缩的，因此引入了范德瓦尔斯体积[24]，可以得到改进后的Keller-Miksis模型，方程如公式（4）所示。

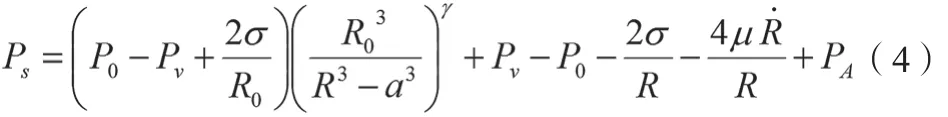
对上述模型使用龙格库塔法进行数值求解，可得到超声空化气泡半径变化曲线，方程中符号含义及仿真时相关参数设置如表1所示。

表1 改进的Keller-Miksis模型中符号的含义与仿真计算时取值

2 结果

2.1 不同传热模式下的超声空化气泡振动情况

本文分析了等温、绝热、等温-绝热3种传热模式情况下单个超声空化气泡壁运动情况。仿真计算中使用的参数如表1所示，改变公式（2）中n的值，结果如图1所示。由图1可见，在3种不同传热模式下，超声空化气泡动力学过程基本一致，都是在约0.43个周期内完成由初始半径R0膨胀到最大瞬时振动半径Rmax，然后在极短的时间内收缩到最小半径，最后振荡并趋于初始半径R0的过程。但是从图中可以发现等温模式下的Rmax/R0大于绝热模式下的Rmax/R0。通过计算可以得到等温过程中R/R0取得最大值5.9565，绝热过程中R/R0取得最大值5.0257，而在等温-绝热过程中R/R0取得最大值5.4264，介于等温过程和绝热过程之间。

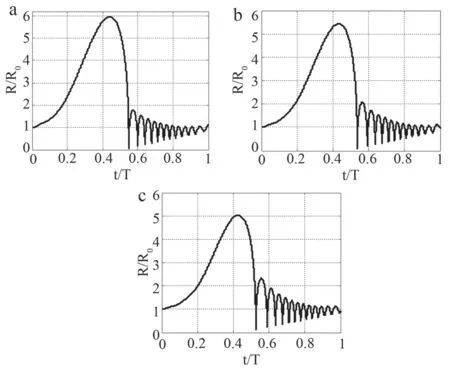
图1 不同传热模式下的空化气泡振动情况

2.2 不同初始半径下的超声空化气泡振动情况

液体中空化气泡在整流扩散和融合的作用下增长到合适大小时，在后续声压的作用下将达到共振半径Rr，对应的自由空化气泡的线性共振频率如公式（5）所示。已知声场频率 fr=f0=30 kHz、γ=1.40、P0=101.3 kPa、σ=0.076 N/m、ρ=1000 kg/m3，此时由公式（5）可以计算得到此频率对应的空化气泡共振半径Rr=110 μm。

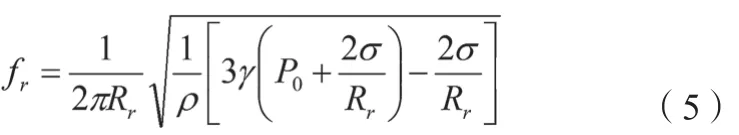
在驱动声波信号PA作用下，设置空化气泡初始半径分别为 2、6、10、40、110、200 μm，由公式（1）、公式（3）和公式（4）可以得到不同初始半径下空化气泡振动半径曲线，结果如图2所示。

由图2a～c可知，当空化气泡初始半径远小于共振半径时，随着空化气泡初始半径的增大，一方面超声空化气泡从初始半径膨胀到最大瞬态振动半径的时间增大，分别是0.3721个周期、0.4403个周期和0.4606个周期，这也导致空化气泡第一次收缩至坍塌所对应的时间增大，超声空化气泡振动持续时间变长；另一方面最大相对振动半径减小，R/R0分别是6.0214、5.9465和4.6664。同时，超声空化气泡坍塌后的振荡频率在减小。由图2d可知，初始半径取R0=40 μm时，该半径小于空化气泡共振半径，空化气泡在负压作用下膨胀，直至达到最大瞬时振动半径，然后在正压作用下收缩，空化气泡崩溃后将产生新的、较小的空化气泡。这些空化气泡在声压的作用下成为空化核，继续呈现出生长、收缩、坍塌的周期性运动。由图2e可知，当初始半径取共振半径Rr=110 μm时，空化气泡在1个周期内经历了膨胀、收缩，可以看到振动半径急剧地趋向于0，发生坍塌之后未产生新的和较小的空化气泡。由图2f可知，初始半径取R0=200 μm大于空化气泡共振半径时，空化气泡会发生复杂的持续振荡，在多个周期内不会发生坍塌。因此，为了得到持续强烈的空化效应，在超声治疗过程中引入额外微泡作为空化增强剂时，应选择半径小于共振半径的微泡。

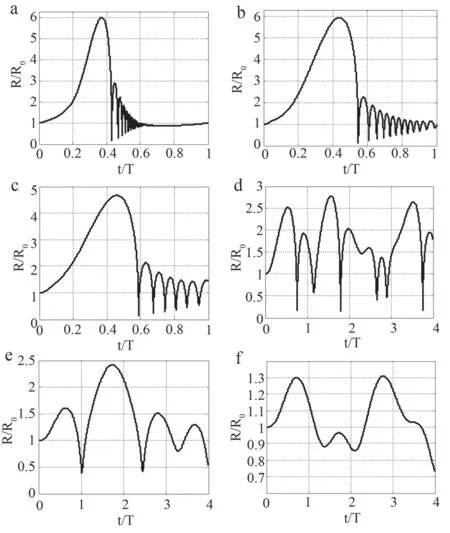
图2 不同初始半径下的空化气泡振动情况

2.3 不同液体表面张力下的超声空化气泡振动情况

本文通过设置不同的液体表面张力σ=0.0327、0.0727、0.2227 N/m，分析液体表面张力对超声空化气泡振动的影响，结果如图3所示。从图3中可以看到，随着液体表面张力的增大，一方面空化气泡的最大瞬态振动半径减小，Rmax/R0分别是6.5709、6.0077和3.3357。另一方面超声空化气泡从初始半径膨胀到最大瞬态振动半径的所需时间减小，分别是0.4513个周期、0.4413个周期和0.3753个周期，这也导致空化气泡第1次收缩至坍塌所对应的时间减小。另外，空化气泡的第1次和随后第2次生长半径的比值随着液体表面张力的增大而减小。因此，在实际的超声空化过程中，为了得到较强的空化效应，应选取液体表面张力较小的液体。

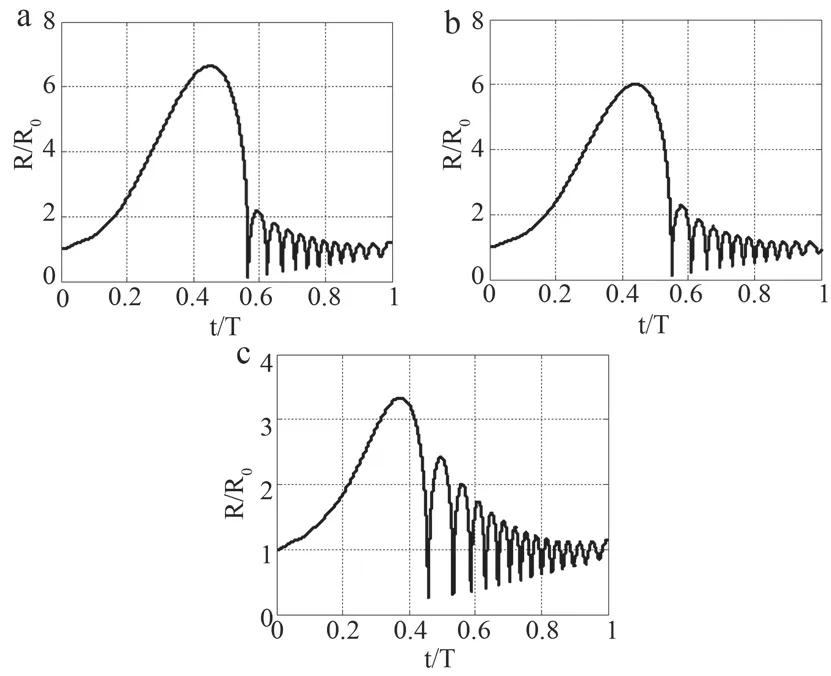
图3 不同液体表面张力下的空化气泡振动情况

2.4 不同液体黏滞系数下的超声空化气泡振动情况

为讨论液体黏滞系数对超声空化气泡振动情况产生的影响，本文选取3种不同的黏滞系数，分别为μ=0.0001、0.001、0.01 Pa·s，其余参数值参照表1，得到的结果如图4所示。从图4可以发现，液体黏滞系数越大，空化气泡的最大瞬态振动半径越小，通过计算得到μ=0.0001、0.001、0.01 Pa·s时 Rmax/R0分别为 6.0457、5.9465和 5.0581。超声空化气泡第一次收缩坍塌后的持续振荡逐渐减弱，当μ=0.01 Pa·s时，空化气泡的振动持续时间明显变短，在声场驱动作用下持续空化效应减弱。产生这种现象的主要原因是空化气泡在发生膨胀时的负声压不足以克服液体分子之间的作用力，这说明液体黏滞系数太大时，会导致超声空化比较难发生。

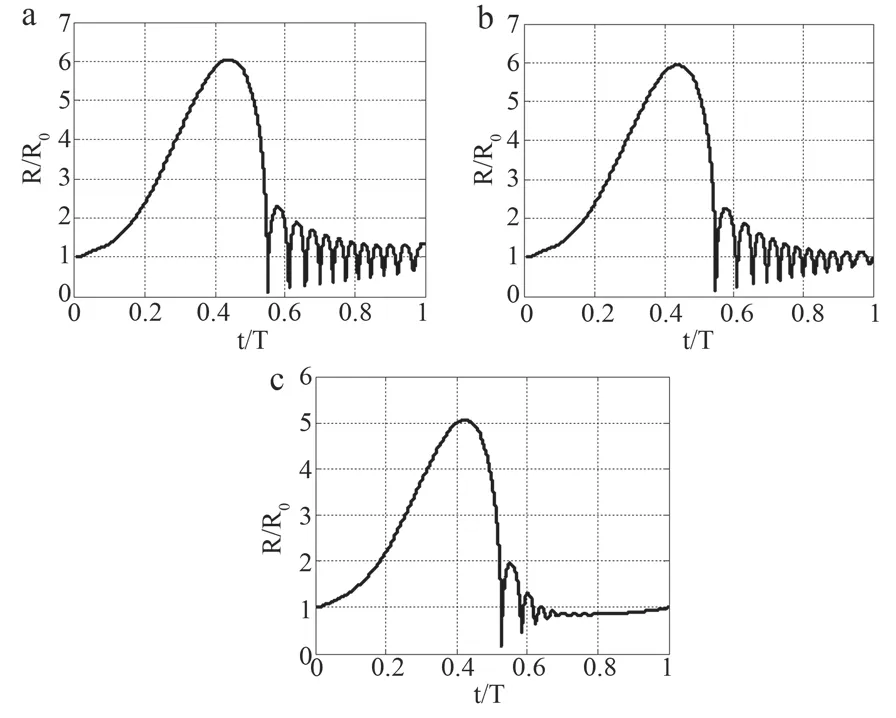
图4 不同液体黏滞系数下的空化气泡振动情况

2.5 不同液体饱和蒸汽压下的超声空化气泡振动情况

为了讨论液体饱和蒸汽压对超声空化气泡振动情况产生的影响，本文选取3种不同的液体饱和蒸汽压，分别为Pv=330、22330、42330 Pa，其余参数值参照表1，得到的结果如图5所示。由图5可知随着液体饱和蒸汽压的增大，一方面超声空化气泡从初始半径增长到最大瞬态振动半径的时间增大，分别是0.4327个周期、0.5086个周期和0.5704个周期，同时空化气泡第一次收缩至坍塌所需要的时间增大；另一方面空化气泡最大瞬态振动半径增大，R/R0分别是5.0261、9.3950和13.1960。另外，在一个周期内空化气泡再生产的次数也减少了，空化效应的可持续性减弱。以上结果表明，液体饱和蒸汽压越大，超声空化效应越弱。

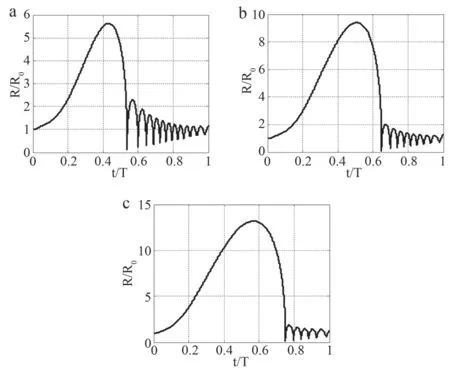
图5 不同液体饱和蒸汽压下的空化气泡振动情况

2.6 不同激励频率下的超声空化气泡振动情况

给定初始半径R0=6 μm ，其余参数值参考表1，本文改变了驱动声场的激励频率，分析激励频率对超声空化气泡振动情况的影响。将Rr=R0=6 μm代入公式（5）可计算得到共振频率fr=0.6 MHz，设置f0=10 kHz、f0=30 kHz、f0=fr=0.6 MHz和f0=2 kHz，结果如图6所示。由图6可知，不同的激励频率下超声空化气泡振动半径曲线是明显不同的。随着激励频率的增大，空化气泡的最大瞬态振动半径明显减小，Rmax/R0分别是7.9651、5.9465、1.5119和1.1036。当f0=10 kHz与f0=30 kHz小于共振频率时，一方面可以看到超声空化气泡经历了生长、坍塌、再产生、生长、坍塌的周期性动力学过程；另一方面空化气泡的振动持续时间明显变长，在声场驱动作用下持续空化效应增强。当f0=fr=0.6 MHz时，空化气泡在1个周期内膨胀到最大瞬时振动半径后，振动半径急剧收缩并趋向于0，崩溃后无新的、较小的空化气泡产生。当f0=2 kHz大于共振频率时，空化气泡振动周期变小，图6d显示的是10个周期内超声空化气泡的振动情况，可以看到空化气泡在做复杂的振荡运动。分析其原因，可能是因为激励频率太大导致空化气泡振动周期变小，在驱动声压负相期间来不及增长或在驱动声压正相期间来不及崩溃[25]。因此，在初始半径一定的前提下，只是增大激励频率对于增强空化效果并不显著，需要设置合适的激励频率来得到较强的超声空化。

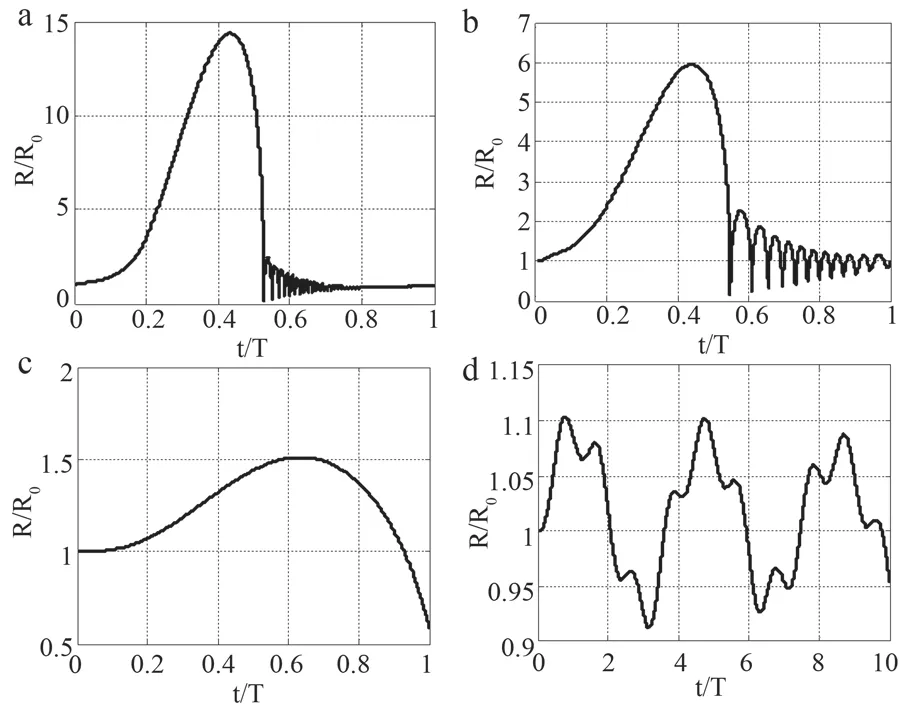
图6 不同激励频率下的空化气泡振动情况

2.7 不同声驱动幅度下的超声空化气泡振动情况

为了分析声驱动幅度对超声空化气泡振动情况产生的影响，本文选取不同的声压幅值Pa=50 kPa、Pa=0.1 MPa、Pa=0.15 MPa和Pa=0.3 MPa进行仿真计算，其余参数值参考表1，结果如图7所示。在其他参数不变的前提下，随着声压幅值的增大，超声空化气泡最大瞬态振动半径明显增大，R/R0分别是1.2155、2.5290、9.6980和26.3603，分析其原因可能是因为声压幅值越大，在驱动声压正、负相交互作用下，超声波对空化气泡的拉伸作用增强，空化气泡运动剧烈。如图7a所示，当声压幅值过小，R/R0较小且空化气泡不会发生崩溃，这主要是因为声驱动幅值太小，导致超声空化气泡难以生长到很大且难以收缩至最小半径从而发生破裂，因此以稳态空化为主，而瞬态空化难以发生。如图7d所示，当声压幅值较大时，超声空化气泡在1个周期内再生产的次数减少，空化效应的可持续性减弱，这主要是因为声驱动幅值太大，导致空化气泡在驱动声压负相作用下增长过大，当驱动声压正相作用时，空化气泡第一次收缩至坍塌所需要的时间增大，导致空化气泡再生产的次数减少。因此，在合理的超声声压范围内，选取较大的声压幅值可以增强空化效应。

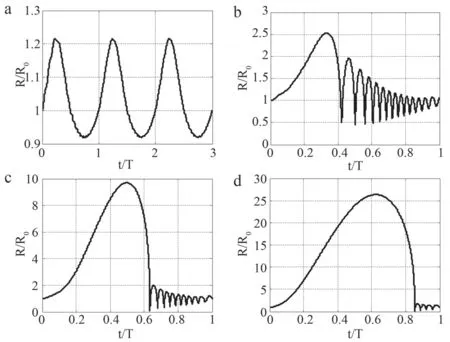
图7 不同声驱动幅度下的空化气泡振动情况

3 讨论

空化效应是诸多超声治疗过程中的关键作用机制。本文在Keller-Miksis模型的基础上，构建了一个改进的超声空化气泡动力学仿真模型。然后使用MATLAB对超声场作用下液体中空化气泡的运动进行数值模拟，系统分析了不同传热模式、空化气泡参数、液体参数和声场参数下的超声空化气泡动力学行为。近年来有研究者对超声作用下液体中的空化气泡运动进行了基础研究，通过建立不同的空化气泡运动模型，对影响空化气泡运动过程的影响因素进行分析[25]。

王捷[25]根据Rayleigh-Plesset气泡运动方程，分析了不同声场信号激励下的单一空化气泡的动力学过程。其中就声场频率、声压和气泡初始半径对气泡动力学过程的影响的研究，得出了以下的结论：给定空化气泡的初始半径，随着声场频率升高，气泡将持续振荡而不崩溃，超声空化将难以发生。在合理的超声声压范围内，提高声场声压会增强空化效应，但过高的声压将使气泡的崩溃推迟，这与本文的研究结果一致。张红等[26]基于声场作用下液体中一个气泡的运动模型，研究了液体中声压幅值、超声频率、空化核半径以及液体的密度、表面张力、动力粘度等因素对气泡运动的影响。仿真结果表明，较低的声压幅值下并不会产生气泡崩溃，但随着声压幅值的增加，气泡振动程度更加剧烈，增强了空化效果；声压幅值一定，设置合适范围内的声频才能达到最佳效果；初始气泡半径、液体的密度、动力粘度和表面张力都会对气泡运动产生一定影响，但初始气泡半径对空化效应影响明显，表面张力的影响并不大，这些结论与本文研究结果一致。崔方玲等[27]通过对空化气泡运动的动力学模型进行数值仿真，探讨了超声频率、声压、空化泡初始半径和绝热指数对空化气泡运动的影响。模拟结果表明，随着超声频率的增加，空化效应减弱；随着声压幅值的增大，空化气泡最大振幅增加；气泡的初始半径较小，空化效果较好；随着绝热指数取值的增大，空化气泡最大振幅略有减小。以上结果证实了本文仿真结果与数值分析的正确性。

本文的方法创新性在于提出了一个考虑因素更全面、更接近实际情况的适用于液体中的气泡壁运动的超声空化气泡动力学仿真模型。该模型不仅考虑了微泡内蒸汽压力、液体粘滞性、微泡表面张力、液体的可压缩性、声辐射效应以及入射声场的影响，同时还充分考虑了传热模式对空化泡振动特性的影响以及气体不可无限压缩的事实。基于改进的模型仿真了不同传热模式对超声空化气泡振动特性的影响以及不同参数下的超声空化气泡动力学特性，研究获得最佳空化效果的物理条件，这为超声空化的广泛应用以及规划和监控超声治疗过程以实现精准高效的超声治疗提供了相应的理论支持，有望揭示超声空化瞬态物理过程。同时这也是能够有选择性地增强或是抑制空化效应的前提，进而能够提高以空化效应为作用机制的超声治疗效率，保障治疗过程的精确性和安全性。

但本文尚存在以下不足：本研究只是基于单个超声空化气泡，并基于改进的模型探讨了不同传热模式、空化气泡参数、液体参数和声场参数对单个超声空化气泡的影响，事实上空化气泡是以泡群的形式存在。因此未来还需基于本文改进的模型，进一步构建双泡以及泡群的模型，并分析不同传热过程、空化气泡参数、液体参数、声场参数以及泡与泡之间的距离对双泡和泡群振动特性的影响，这对于丰富微泡群动力学理论和指导实验研究都具有重要的意义。在超声场作用下的微泡群动力学建模和相应的理论机制将是未来主要的研究方向。本文改进的基于单泡的超声空化气泡动力学仿真模型，对声场中气泡壁运动的描述更加接近实际情况，这为后续微泡群的动力学模型研究提供了有价值的信息。

4 结论

为了提高以空化效应为作用机制的超声治疗效率，本文基于Keller-Miksis模型，构建了一个可描述、更接近实际情况下的声场中气泡壁运动的模型，并对不同参数下超声空化气泡振动情况进行了讨论，得出以下主要结果：① 在等温、等温-绝热、绝热3种不同传热模式下，超声空化气泡动力学过程基本一致，最大瞬时振动半径依次减小；② 空化气泡初始半径小于共振半径时可以增强超声空化效应；③随着液体表面张力和液体黏滞系数的增大，空化效果变弱；随着液体饱和蒸汽压的增大，超声空化效应减弱；④ 在初始半径一定的前提下，需要设置合适的声场激励频率来增强空化效果；⑤ 在合理的超声声压范围内，选取较大的声压幅值可以增强空化效应。基于本文改进的模型，未来将进一步研究双泡以及泡群的动力学行为，并实现超声空化成像。