由粗到细的多级小波变换水下图像增强

袁国铭，杨光，王金峰，刘海军，王薇

（1.防灾科技学院 应急管理学院，河北 三河 065201；2.防灾科技学院 信息工程学院，河北 三河 065201）

1 引言

水下成像被广泛用于海洋资源勘探、水下环境监测、海底目标识别等领域，然而受光在水中传播时散射和衰减效应的影响，水下图像往往呈现模糊、色彩失真、可视度低等退化现象。水下图像增强作为水下图像清晰化处理的重要方法被广泛用于水下机器视觉任务中［1］。

常用的水下增强方法可分为物理模型增强法，非物理模型增强法和深度学习增强法［2-5］。物理模型的增强法利用已有的先验信息求解水下成像模型中的清晰图像，具有高效简洁的优势。例如Drews等人［6］提出了水下暗通道先验，即在清晰水下图像的局部邻域内，总有像素在蓝或绿通道中具有非常低的灰度值，甚至趋于零。Asadi等人［7］将颜色校正与暗通道先验相结合，进一步提出了优化的暗通道先验增强算法。虽然知识先验有助于物理模型估计清晰的水下图像，但不能描述复杂的水下环境，泛化能力较差。

非物理模型的增强方法旨在修改水下图像的像素值，以达到视觉满意的增强效果。Li等人［8］提出了融合白平衡与直方图拉伸的方法（Hybrid Framework for Underwater Image Enhancement，HUIE），来实现水下图像的颜色补偿。Song等人［9］提出的水下图像增强方法（Enhancement Registration Homogenization，ERH），通过顺序执行增强、配准和均匀化的方式来获取高质量的水下图像。为进一步增强细节，Hu等人［10］提 出 了小波变换 增 强 算 法（Enhancement based on Wavelet Transform，EWT），该法将水下图像分为高频和低频部分，对低频部分实施直方图均衡化操作以校正颜色，对高频部分实施对数计算以增强细节。最后实施反小波变换，得到增强的水下图像。然而，上述算法仅能针对某一种或几种水域图像进行增强，应用范围有限。

近年来，基于神经网络的水下图像增强方法备受关注，它通过学习水下图像与清晰图像之间的映射关系实施增强，具有较好的泛化能力。例如，Anwar等人［11］提出了水下增强神经网络（Underwater Enhancement CNN，UWCNN）方法，它利用10种Jerlov水类型的图像分别训练UWCNN模型，能有效处理不同水域图像的颜色差异。Wang等人［12］提出了水下生成对抗网络（Underwater Generative Adversarial Network，UWGAN），利用生成对抗网络复原真实的水下图像，具有较好的鲁棒性。Islam等人［13］提出全卷积条件生成对抗网络（Full Convolutional Conditional GAN based Network，FGAN），并用多模态目标函数来训练网络模型，获得逼近真实场景颜色的视觉效果。近年来，更多学者将传统增强算法和数学理论融入神经网络的设计中，取得了较好的图像增强效果。如He等人［14］，将常微分方程（Ordinary Differential Equation，ODE）的一阶欧拉求解策略映射为残差模块，提出了ODE启发的图像增强模型，该模型因融入了欧拉算法的稳定性和收敛性，具有好的网络性能。Ma等人［15］将小波变换后的高频和低频信息作为增强网络的输入，并利用小波双流网络（Wavelet-based Dual-stream Network，WDN）的高低频分支分别处理高低频的信息，然而双流分支的设计未考虑频率域信息属性，颜色及细节的增强效果有待提高。Sun等 人［16］提 出 了 多 级 小 波 卷 积 网 络（Multi-level Wavelet CNN，MWN），它利用多级小波变换和反变换来实现水下图像编码和解码，融入的边缘增强信息，能有效实现细节增强。Zamir等人［17］将传统方法中由粗到细的复原策略引入到图像复原框架，从而将复原工作分解为更小，更容易的子任务，以便高效实施图像去雨、去噪和去模糊。上述算法或关注颜色校正，或关注边缘增强，或关注结果细化，不能同时实施颜色校正，细节增强及结果细化，获得满意的结果。

本文提出了由粗到细的多级小波变换水下图像增强网络，它包含多级小波变换的图像增强子网络和二阶龙格库塔模块的细化子网络，用以校正颜色，增强细节和细化结果。具体来说，首先，利用多级小波变换将水下图像分解为低频图像和一系列高频图像。随后，在多级小波变换的图像增强子网络中，设计融入实例归一化和位置归一化的低频分支，以消除低频图像中不同水域类型带来的颜色差异。同时，联合低频和高频信息设计基于掩模增强的高频分支，用以增强高频图像中的边缘和细节；实施反小波变换，获得初步增强的水下图像。设计ODE启发的二阶龙格库塔模块，并用此构建细化网络，对初步增强的结果进一步细化。实验表明，本算法较已有的水下图像增强算法，具有更好的增强效果，PSNR值的提升幅度达9%。满足水下视觉任务的颜色校正，细节增强，清晰化要求。

2 由粗到细的多级小波变换水下图像增强

本文提出了由粗到细的多级小波变换水下图像增强网络，它包含由粗到细的两个阶段，分别为：多级小波变换的图像增强子网络和二阶龙格库塔模块构建的细化子网络。网络框架如图1所示。

对于输入的水下图像I∈Rh×w×3，首先利用多级Haar小波变换将I分为多个频率带，以便根据不同频率带包含的信息，实施相应的图像增强操作。具体来说，Haar它包含低通滤波器L和高通滤波器H：

对I实施低通滤波LLT，得到低频图像IL∈Rh/2×w/2，对 图 像I实 施LHT，HLT，HHT滤波，则得到垂直，水平，对角线方向的高频图像IH=[ILH，IHL，IHH]，IH∈Rh/2×w/2。对 低 频 图 像重复实施小波变换，可实现二级，三级以至多级小波变换。假设n为小波变换的级数，实施多级Haar小波变换后，得到低频图像InL，尺寸为h2n×w2n，高 频 图 像InH，In-1H，In-2H，尺 寸 为h2n-1×w2n-1，默认n=3。

2.1 多级小波变换的图像增强子网络

对于包含颜色信息的低频图像InL，旨在消除不同种水域类型产生的颜色差异，这里将颜色校正问题看作隐式的类型转化问题，并设计基于实例归一化和位置归一化处理的低频分支。对于包含细节的高频图像InH，In-1H，In-2H，旨在如实地增强细节。为减少计算成本，联合第n级小波分解获取的低频和高频信息计算掩模，并设计基于掩模增强的高频分支。在对高低频图像实施处理后，利用逆小波变换，得到初步增强的结果。

2.1.1 低频分支设计

本文将低频图像的颜色校正问题看作隐式的风格转换问题，并将风格转换中常用的实例归一化（Instance Normalization，IN）和位置归一化（Position Normalization，PN）用于低频分支的设计中［18］。这里，IN具有空间域中内容对比度的不变性，而PN能在通道空间中捕获图像的类型和形状信息。将IN和PN引入低频分支设计中，能在空间和通道域里自适应地调节输入特征的均值和方差，消除颜色差异。PN和IN均可由式（2）解释：

式中：u和σ为特征的均值和标准方差。u'和σ'为从输入特征中学习的仿射参数。

低频分支的结构如图1所示，首先利用两个卷积对第n级小波变换（n=3）的低频图像InL逐步实施通道扩展，得到特征FL。随后对FL实施PN操作，即提取所有通道数下的特征均值uc和方差σc：

图1 由粗到细的多级小波变换水下增强网络框架Fig.1 Architecture of coarse-to-fine network for underwater image enhancement based on multi-level wavelet transform

式中：b，c，h，w分别为特征FL的批大小，通道数，高和宽。c'为通道索引。归一化的FL输入到文献［18］中所提的5个ResIN模块中，该模块包括1个 卷 积 层，1个IN层，1个ReLU激 活 函 数 以 及残差连接。其中，IN的特征均值uhw和方差σhw计算公式如式（5）和式（6）：

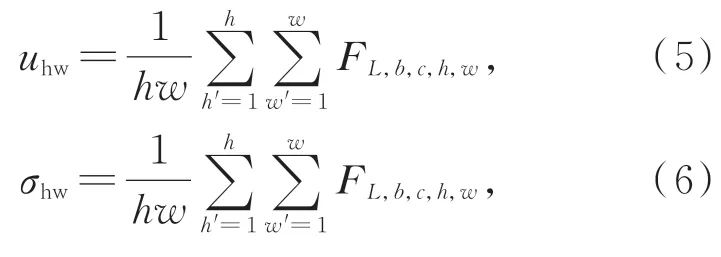
式中：h'和w'为高和宽的索引，h，w为特征的高和 宽。FL，FL，b，c，h，w同 公 式（3）和（4）中 的 变 量。IN操作摒弃了提取的空间统计信息如uhw，σhw，而所学的仿射参数u'hw和σ'hw能有效消除不同水域类型导致的颜色差异；最后ResIN输出的信息进一步由PN所学的仿射参数u'c，σ'c调整（见图1），并通过一个卷积将通道数减少至与InL相同的通道数，得到InL'。

2.1.2 高频分支设计

本文将高频分支的细节增强处理，看作为低频分支实施风格转换时的对应操作。为了能如实地增强水下图像，细节的增强需与低频分支实现InL至InL'风格转换操作保持一致，因此本文拟利用InL，InL'信息来实现InH的增强。然而，具体如何实施InH的增强操作，仍是有待解决的问题。图2显示了初始的水下图像（图2（a））及增强的水下图像（图2（c））在分别实施一级小波变换后获取的2张高频图2（b）及图2（d）。他们在细节分布上基本一致，仅在亮度上存在差异，如图2（d）中箭头所示的细节点，相比图2（b）中对应位置处的细节点亮度更亮。因此，本文拟联合InL，InL'及InH生成细节增强掩模，并将掩模与高频图像InH相乘，以便自适应地调节全局亮度信息。值得一提的是，掩模的生成，不但利用了低频分支风格转换的颜色信息InL，InL'来调节全局亮度，确保细节增强与低频分支实施风格转换操作保持一致，还利用了包含细节的高频图像InH信息，故增强操作能同时兼顾细节及亮度。细化高频图像的掩模Mn的计算表达式如式（7）所示：

图2 初始图像及增强图像的比对Fig.2 Comparison between initial images and enhanced images

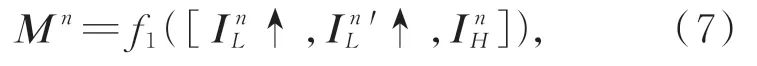
式中：↑为双线性插值上采样操作，它将尺寸为h2n×w2n的InL和InL'上采样至h2n-1×w2n-1，以便与InH尺度匹配；[⋅]为串联操作；f1为复合操作的函数，该复合操作包含2个卷积层和5个去除IN操作 的Res模块［18］。InH为高频图像。最后 的卷积层将输出通道为3的掩模Mn。利用Mn细化InH，以得到细化高频图像InH'，具体表达式如式（8）所示：

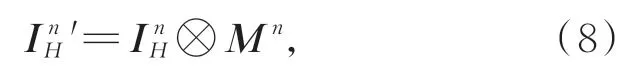
式中，⊗为点乘操作。

实际上各级小波变换获得的高频图像包含相同的细节和纹理信息，仅在微小细节上存在差异。如图3所示，初始水下图像（图3（a））的一、二、三级小波变换高频图像IHH（见图3（b）～3（d）），仅在沙粒细节上存在差异，即随着小波分解的级数越多，沙粒细节越少。为提高计算效率，本方法在第n级小波变换的高频分支上计算掩膜Mn，并上 采 样 及细化后，对n-2，n-1级小波变换的高频图像进行全局的细节增强。

图3 各级小波变换获得的高频图像Fig.3 High frequency image obtained by wavelet transform at different levels

具体来说，可对Mn实施双线性插值上采样，得到细化In-1H，In-2H的掩膜Mn-1，Mn-2。表达式为：

式中：↑为双线性插值上采样，它们分别将n级小波变换时获取的掩模Mn和n-1级小波变换时获取的掩模Mn-1尺度上采样至In-1H，In-2H的相同大小；f2和f3为复合操作的函数，它们均包含2个3×3的卷积层，用于细化上采样掩膜。依据公式（8），即 可 得到 细 化 的In-1H'，In-2H'。对InL'，InH'，In-1H'，In-2H'实 施 逆 小 波 变 换，获 得 增 强图像I'。

2.2 二阶龙格库塔模块构建的细化子网络

堆叠的残差模块被广泛地用于图像复原的细化中［14］。实际上，残差模块可看成是ODE前向欧拉求解策略的映射，堆叠的残差模块可视为离散的一阶欧拉逼近ODE求解过程。为获取更优的增强结果，本文设计了基于二阶龙格库塔（Runge-Kutta）模块的细化子网络。具体来说，一阶ODE问题可由一阶微分方程及初始条件实施求解：

式中：f(t，y)为变量t，y的函数，dydt为函数y对自变量t的一阶导数，y(t)∈Rd为自变量t的函数y，且t≥t0，y(t0)=v为初始条件。

依据一阶的欧拉求解策略，dydt可表示为离 散 形 式(y(tn+1)-y(tn))(tn+1-tn)，n=0，1，…，n，则公式（11）可用式（12）来表示：

式中，h=tn+1-tn。研究表明残差模块也有相似结构：

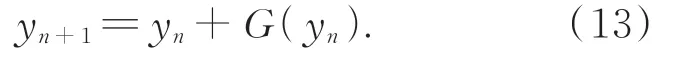
由此可见，若将式（12）中的y(tn+1)和y(tn)分 别 看 成yn+1和yn，而G(yn)=hf(tn，y(tn))，则残差模块即为一阶欧拉方法的映射模块，在细化网络中堆叠的残差模块，则可视为离散的欧拉逼近求解过程。考虑到二阶龙格库塔方法相比于一阶欧拉方法，具有更小的局部截断误差及稳定性［19］，能更精确地求解ODE，本文设计基于二阶龙格库塔的RK2模块，并堆叠5个RK2模块构建细化网络，由此将二阶龙格库塔方法的优越性引入到网络性能中，获得更佳的细化效果。

二阶龙格库塔模块设计如下。

由数值ODE理论可知，二阶龙格库塔方法利用梯形公式来实施求解：

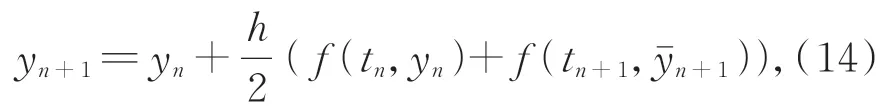
式 中：tn+1可 由tn+1=h+tn计 算 得 到；yˉn+1可 用它的一阶逼近，即公式（13）的yn+1来替代。依据公式（13）中G(yn)=hf(tn，y(tn))的映射关系，可获得表达式（15）～式（17），由此得到RK2模块结构图如图4所示。

图4 RK2模块结构Fig.4 Architecture of RK2 block

2.3 损失函数

在模型的训练过程中，我们通过最小化L2函数来减少图1中I'，J与真实结果G之间的差异。假设I'i，Ji和Gi，i=1，2，…，m为一组小波变换增强图像，细化网络增强图像和真实水下图像，则对应的损失函数L可表示如式（18）：

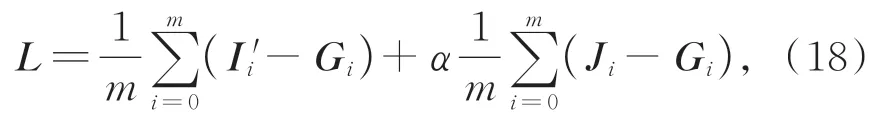
式中：α为平衡系数，默认取1。

3 实验结果与分析

3.1 数据集

为确保由粗到细的多级小波变换水下图像增强网络具有较好的泛化能力，本文拟选用文献［11］提供的数据集来进行训练和测试。该数据集依据水下成像物理模型对1 449张NYU-V2室内图像进行水下成像合成，即每张图像合成I，IA，IB，II，III，1，3，5，7，9共10种水域类型的图像，共计合成图像14 490张，其中13 041张图像为训练集，1 449张图像为测试集1（文中标记为Test1）。另一方面，选用文献［20］提供的890张真实水下图像及其高质量参考图像为测试集2（文中标记为Test2），这里高质量参考图像是由25位从事图像处理领域的志愿者和25位从事其他领域的志愿者，共同从12种水下图像增强算法的结果中逐一挑选出来。为客观评价各算法增强结果的质量，采用全参考的图像质量评价指标：信噪比/相似度PSNR/SSIM、局部批次对比度PCQI、边缘强度EI，以及无参考图像质量评价指标：UIQM，UCIQE和信息熵Entropy。其中，PSNR/SSIM，PCQI及EI在合成及真实图像测试集的真实（参考）图像帮助下，测量增强图像的质量，对比度变化及边缘强度，其值越高则增强算法的性能越好。另一方面，非参考的评估指标UIQM是基于人眼系统激励的无参考水下图像评价指标，它利用色调、对比度和清晰度的加权组合来综合评价水下图像的质量，避免了单一指标评价的局限性，其值越高，水下图像的质量越好。与UIQM类似，UCIQE是用CIELab空间 的色度、饱和度、对比度的线性组合来评价彩色水下图像的质量，其值越高，图像质量越好。Entropy能反映图像中信息量，值越大包含的信息越多［21］。

3.2 算法实施细节

水下图像增强网络在NVIDIA RTX 2080 Ti GPU的PC机 上，通 过 搭 建Pytorch深 度 学 习框架实现。网络框架中小波变换级数n=3，共包含12个 卷 积 层，5个ResIN模 块，5个Res模 块，2个 上 采样操作及5个RK2模 块，其中ResIN模块参数设置为文献［18］中ResIN模块的默认设置，因Res模块为去除IN操作的ResIN模块，故参数同［18］。上采样采用双线性插值法，模型中12个卷积层及RK2中涉及的卷积层共有两种不同的参数设置：图1（彩图见期刊电子版）中蓝色卷积层，核大小为1×1，步长为1，填充为0。其余绿色卷积层，核大小为3×3，步长为1，填充为1。各层/模块输出通道数标于图1各层/模块下方。

优化函数Adam算法的学习率为0.000 1，β1=0.9，β2=0.999。训练及测试时的输入图像大小均为512×512，批大小为4，训练200 epochs。

3.3 网络结构及参数分析

水下图像增强网络包含多级小波变换的图像增强子网络和二阶龙格库塔模块构建的细化子网络。其中，多级小波变换图像增强子网络的低频分支和高频分支分别包含5个ResIN模块和5个Res模块，细化子网络中则包含5个RK2模块，模型在Test1上结果为24.51/0.886 7。为了验证构建模块数的有效性，本节首先分别测试不同组件包含的不同模块数时网络的性能，即高频分支包含Res模块数为3，4，6时，对应变异模型Res_3，Res_4，Res_6的性能；低频分支包含ResIN模块数为3，4，6时，对应变异模型ResIN_3，ResIN_4，ResIN_6的性能；细化子网络 包 含RK2模 块 数 为3，4，6时，应 变 异 模 型RK2_3，RK2_4，RK2_6的 性 能。结 果 如 表1所示，当网络结构不变，增加任一模块（ResIN模块，Res模块或RK2模块）数量时，网络性能均有不同程度的提升，但当ResIN模块增至6时，性能微微下降，而增加Res和RK2至6时，其量化结果虽高于所提模型结果24.51/0.886 7，但差距微小。为平衡网络参数和性能，所提模型设置的模块数最优：ResIN模块，Res模块及RK2模块的数量均为5。在此基础上，讨论多级小波变换的图像增强子网络及细化子网络结构设计的优越性。

表1 测试集1上不同构建模块数的模型量化结果对比Tab.1 Comparison of quantitative results by variant models with different number of building modules on Test 1.

为验证多级小波变换的图像增强子网络有效性，本文分别测试了小波变换级数n=1，2，3，4，5，6的情况，相应的变异模型在合成图像测试集上的量化结果如表2所示，从中可见，随着n增加，网络性能逐步提高，当n=3时，模型能获得最高的PSNR和SSIM，此后随着n增加，网络性能略微下降，但仍具有较好的鲁棒性，如n=4较n=3而 言，PSNR值 仅 从24.51下 降 到24.48，为平衡计算成本和精度，本文选择n=3为小波分解级数。

为验证图像增强子网络的有效性，设计了两个变异模型：Net-w/o-lb和Net-w/o-hb。Net-w/o-lb在保持所提网络结构不变的基础上，将n级小波变换（n=3），低频分支中的PN和ResIN移除，仅保留图1低频分支中两个卷积操作，以验证低频分支颜色校正的有效性。Net-w/o-hb则在原网络模型的基础上，移除掩模计算及相乘操作，直接将各级小波变换获得的高频图像，输入到两个卷积层中，得到处理后的高频信息，以验证高频分支实施掩模增强的有效性。如表2所示，Net-w/o-lb和Net-w/o-hb在合成图像测试集上的量化结果低于所提网络模型（n=3）的结果，证明高频分支及低频分支能有效提升水下图像增强的性能。

表2 测试集1上不同变异模型的量化结果对比Tab.2 Comparison of quantitative results by different variant models on Test1.

为验证ODE启发的细化子网络及其构建模块RK2的有效性，设计了Net-w/o-R和Net-Res变异模型。Net-w/o-R将原始网络中的细化网络移除，即将基于多级小波变换的水下图像增强子网络输出结果I'作为最后的增强结果，以验证细化网络的有效性。Net-Residual则将细化网络中RK2模块替换为残差模块，以验证RK2模块的优越性。两个模型在合成图像测试集上对应的测试结果如表2所示，较所提网络而言，变异模型的性能明显下降，从而证明基于RK2模块的细化网络有效性和必要性。

为验证训练参数epoch设置的合理性，视觉化训练过程中loss函数值曲线及每个epoch时训练模型在Test1上的PSNR值。如图5所示，随着epoch数的增加，loss值不断降低，且在约180 epochs时模型收敛。图6同理，模型训练过程中测试集的PSNR值也在约180 epochs时趋于稳定。因此，将模型训练次数设置为200 epochs能确保模型收敛，获得最优性能的网络模型。

图5 训练过程中loss函数值Fig.5 Loss curves during training.

图6 训练过程中测试集的平均PSNR值Fig.6 Average PSNR of testing data during training.

3.4 合成水下图像增强结果对比

为评测所提网络模型的增强效果，本节将在合成水下图像测试集Test1上，比较本文算法与8个已有的水下图像增强算法的性能，包括传统的HUIE算法［8］，ERH算 法［9］，EWT算法［10］以 及基 于CNN的UWCNN算 法［11］，UWGAN算法［12］，FGAN算 法［13］，WDN算 法［15］，MWN算法［16］。其中，UWCNN算法分别采用10种不同水类型的图像训练，得到10个水下增强模型，本文选取水域类型为1的水下图像训练模型进行测试。表3为各算法的量化结果，从中可见本文算法具有最高的PSNR与SSIM值，表明本文算法的优化结果最接近真实结果。此外，最高的UCIQE，UIQM和PCQI值，也说明本文算法能更好地平衡水下图像的色调、对比度、清晰度及饱和度。在PCQI，Entropy和EI指标上，本文算法的量化结果也高于比较算法，证明本文算法有效地增强场景细节，而不是噪声。

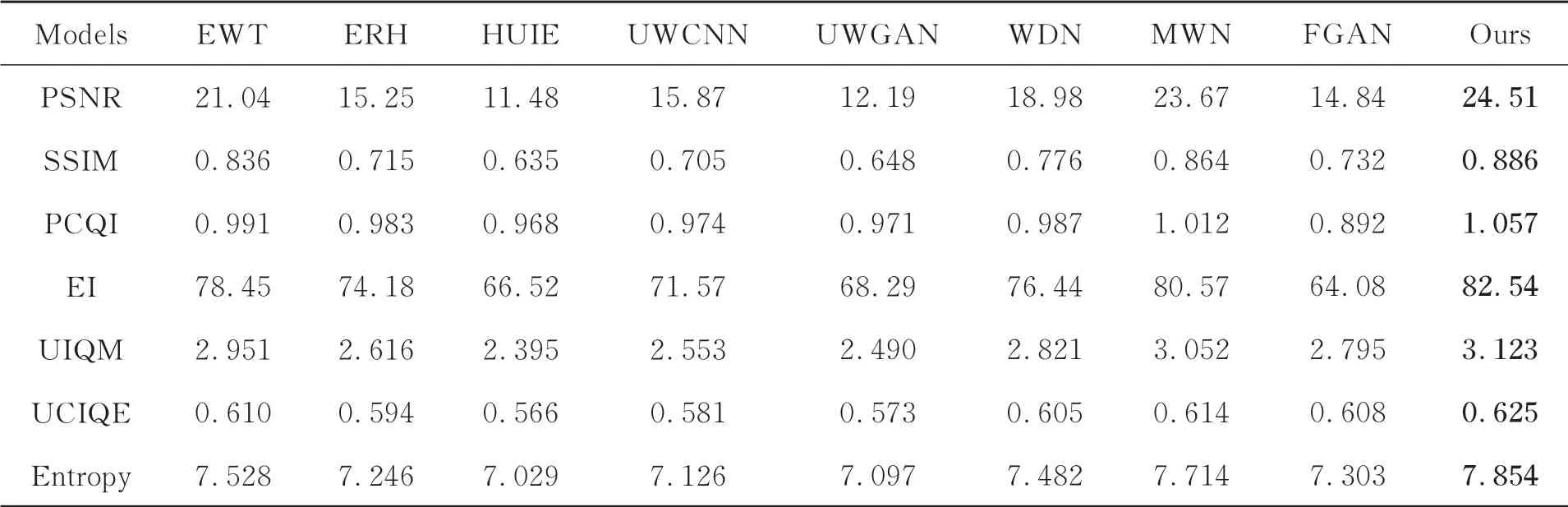
表3 不同算法在测试集1上的量化结果对比Tab.3 Quantitative comparison of enhanced results by different algorithms on Test1.

为进一步对比视觉增强效果，从Test1中选取了3张水下图像进行展示，包括合成的浑浊水域图像，低照明图像，蓝绿色水域图像（见图7（a））。各算法的视觉增强结果如图8（a）～8（i）所示。结果表明，EWT算法能拉伸图像的对比度，提高低照明图像的亮度，并在一定程度上增强水下图像的细节，但对于蓝绿色水域图像，仍存在颜色失真和细节丢失的问题，如图8（a）第3行。ERH算法虽有一定的颜色校正能力，但增强结果（见图8（b））整体偏暗，细节丢失严重，与真实结果（见图8（j））的差异较大。HUIE算法，UWCNN算 法，UWGAN算法和FUnIEGAN算 法 结果存在明显的色偏现象，如图8（c）第1行结果偏蓝，而图8（d），8（e），8（h）结果偏黄，且增强结果出现一定程度的模糊。WDN及MWN方法能有效去除色偏，增强细节，但对蓝绿水水域图像的增强效果较差，图8（f）和8（g）的背景呈现出失真的暗红色，且细节模糊。相比而言，本文算法的结果图8（i）在亮度，清晰度及色差平衡力方面明显优于已有的增强算法，且纹理细节信息也更加突出，接近于图8（j）的真实结果。图8下方标出的PSNR/SSIM值进一步证明了本文算法的有效性（彩图见期刊电子版）。

图7 测试案例Fig.7 Testing samples

图8 合成水下图像增强结果对比Fig.8 Comparison of enhanced results on synthetic underwater images

3.5 真实水下图像增强结果对比

为验证所提算法的泛化能力，在包含890张真实图像的Test2测试集上进行对比实验。由于Test2提供了真实水下图像的参考图，故可量化各算法的增强结果。图9为不同算法对3幅真实水下图像（图7（b））增强的视觉对比图，包含绿色水域图像，蓝色水域图像及浅水域图像，图9（a）～图9（h）为对比算法的增强结果，图9（i）为本文算法结果，图9（j）为增强参考图像（彩图见期刊电子版）。为了更好地观察细节，图9的第2，4和6行分别为第1，3和5行的细节放大图。从图9可见，EWT因引入了多级小波变换的增强策略，具有较好的视觉增强效果，但在颜色校正上，出现了红通道过度补偿的问题，如图9（a）第1，2行的手和第5，6行岩石的颜色均偏红。ERH，UWCNN，UWGAN，WDN和FUnIEGAN算法结果存在色调失真，如图9（b），9（d），9（e），9（f），9（h）的第3，4行背景偏暗，与真实情况不符。HUIE算法结果出现了部分增强区域，色度不自然的问题，如图9（c）第4行鱼的色度过亮。MWN算法具有较好的增强效果，但对细节丰富的岩石，仍具有边缘模糊现象，如图9（g）第4行。本文算法的结果图9（i）具有最好的清晰度和对比度，其细节甚至比图9（j）的增强效果更佳，如图9（h）第2行手部相较图9（j）更接近真实颜色。图9下方标出的PSNR/SSIM值进一步证明了本文算法的强泛化能力。

图9 真实水下图像增强结果对比Fig.9 Comparison of enhanced results on real underwater images

此外，各算法增强结果的量化指标值如表4所示，本文算法在各指标上仍具有最高值，其中PSNR值较已有算法提高了至少9%，可见客观评价和主观评价相符。为了更直接地展示不同算法在不同数据集上的性能，图10分别为各算法在Test1和Test2上平均PSNR。从中可见，ERH，HUIE，UWGAN，FGAN算法在真实图像集Test2上具有较合成图像集Test1上更好的增强效果，而EWT，UWCNN，WDN，MWN及本文算法则在合成图像集Test1上具有较真实图像集Test2上更好的增强效果。这是由于，ERH，HUIE，UWGAN，FGAN算法面向真实水下图像实施增强，旨在获取逼近真实场景的视觉效果，而本文算法及EWT，UWCNN，WDN，MWN算法利用不同水类型的合成图像实施训练，训练集中未能包含真实场景中所有复杂的降质情况，故出现性能下降。在后续的工作中，将考虑真实图像的信息分布情况，提高稳定性和泛化能力。

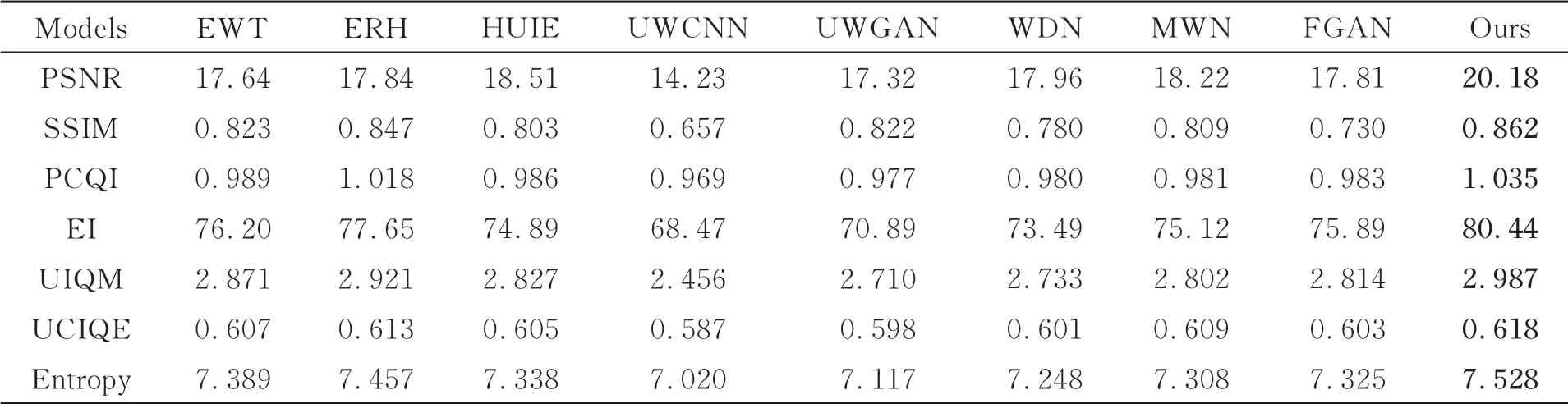
表4 不同算法在测试集2上的量化结果对比Tab.4 Quantitative comparison of enhanced results by different algorithms on Test2.

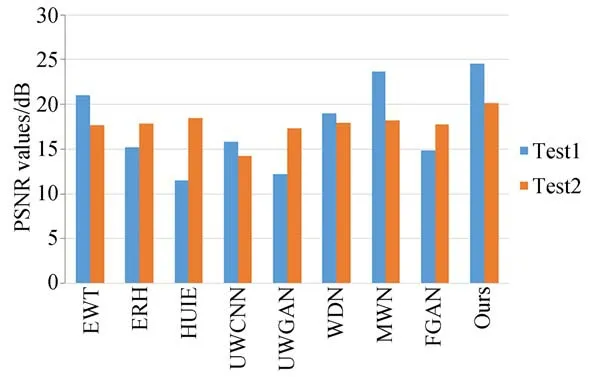
图10 各算法在Test1和Test2上的PSNR值Fig.10 PSNR of different algorithms on Test1 and Test2.

4 结论

为实现水下图像的颜色校正和细节增强，本文提出了由粗到细的多级小波变换水下图像增强网络，它包含多阶小波变换的图像增强子网络和二阶龙格库塔模块构建的细化子网络。多阶小波变换的图像增强子网络用于初步估计水下图像增强的结果，它利用多级小波变换将水下图像分解为低频图像和一系列高频图像，并设计相应的低频分支和高频分支分别处理低高频图像。低频分支利用类型转换中常用的实例归一化和位置归一化操作实现低频图像的颜色校正。高频分支联合高低频信息计算增强高频图像的掩模，来实施细节和纹理的增强。随后，实施反小波变换得到第一阶段估计的水下增强图像。为进一步细化增强结果，设计了ODE启发的二阶龙格库塔模块，它具有较残差模块更好的稳定性和收敛性，用此构建细化网络具有更优的细化结果。实验结果表明，在合成和真实水下图像集上，本文算法具有较好的视觉和量化增强效果。然而，算法虽利用不同水类型的合成图像实施训练，但训练集中仍未能包含真实场景中所有复杂的降质情况，故算法在真实图像数据集上的性能较合成图像数据集上的性能低。在后续工作中，将在模型的设计和训练中更多地考虑真实图像的信息分布情况，提高模型的稳定性和泛化能力。