精密跟踪型望远镜适配的快速星图匹配

刘德龙，杨文波，柳鸣，康喆，李振伟

（中国科学院 国家天文台长春人造卫星观测站，吉林 长春 130117）

1 引言

近年来，大气层外围的卫星、空间碎片、火箭箭体和载荷等人造物体不断增加，空间环境不断恶化，严重威胁了航天器的正常运行，为此需要对目标进行精密定轨、编目、预报及特征分析。基于地基望远镜的光电观测目前仍是最有效的空间目标研究手段之一，它具有观测轨道高度广、组网成本低、无接触及免干扰等优势。其中，精密跟踪型望远镜通过较长弧段观测，取得已知轨道目标的定位数据，为其精密定轨服务［1］。天文定位基于背景恒星的绝对位置克服了轴系定位中机械误差、脱靶量测量误差和坐标系转换等带来的影响，可显著提高空间目标的定位精度。

星图匹配是天文定位中不可或缺的一环，它将观测图像中恒星的摄影坐标和标准星表中的天球坐标关联起来，以此解算观测系统的底片模型。星图匹配主要依靠子图同构［2-3］和模式识别［4-5］。子图同构中的三角形相似算法仍是至今使用最广泛和有效的星图匹配算法，然而传统算法由于特征维数较低，并且需遍历所有星象，导致匹配效率低，导致既耗时又浪费存储空间［6］。随着望远镜光学口径和视场的不断增大，视场中的星象呈指数级增加。同时天文相机技术也不断进步，越来越多望远镜配备了高帧频、高分辨率的科学级CMOS相机。这导致在一个观测周期内图像序列的帧数和每帧数据急剧增加，进一步凸显了传统三角形匹配算法的不足。近年来见诸报道的一些改进算法包括：2019年王军等人［7］采用三角形外接圆和内切圆半径乘积作为匹配特征，初步筛选后再进行三角形三边匹配，2020年刘先一［8］采用径向特征量缩小了待匹配导航星数量，增强了匹配的针对性；2021年李变等人［9］公开的发明专利提出基础三角形的概念，预筛选观测三角形，降低了匹配量；2021年徐伟等人［10］选择观测星中星等最小的三颗组成特征三角形，后采用三边组合特征值的方式进行导航星表的遍历匹配；2021年熊琨等人［11］的专利也提出缩减导航星，并建立导航星角距库的思想。这些算法增加了星表或观测星预处理的复杂度，提高了计算成本；前期预选还有可能造成匹配失败，因此不满足序列图像的首帧星图匹配中容易实现和成功率高的要求。

精密跟踪（简称精跟）型望远镜具有高精度的控制伺服和较大的相机靶面。其图像序列的特点首先是目标和背景恒星的相对运动，由于望远镜跟踪目标，恒星星象会出现拉长。因此需使用短曝光或采用星象模糊还原算法，前者增加了图像噪声，后者使得提取位置发生改变。这均需要匹配算法对于不同天区、轨道和类型的目标具有一定鲁棒性，能够自动选取误差容限进行运算；第二，码盘可在拍摄图像的同时获取望远镜指向，即图像中心的轴系定位。该指向较为粗略，但可用于定位星表。同一观测圈次内序列图像帧间的指向改变量非常精准，可用于快速匹配；第三，望远镜指向连续变化，并且帧间变化较小。因此相邻帧的底片常数变化很小，可用上帧常数进行匹配，之后通过匹配更新底片常数；第四，相对于固定方向观测，精跟型望远镜在观测周期内动作范围较大，因此分区指向模型可能会造成结果误差的不连续。基于以上特点本文提出一种专门适配的星图匹配算法。

2 星图匹配模型

望远镜电控系统根据引导数据驱动跟踪，同时采集图像。后经图像处理和目标识别给出目标和背景恒星的位置。对于精跟型望远镜较小的视场（＜2.5°），六参数模型即可完成匹配。

由于拍摄图像和实际星图只存在比例、平移、旋转或镜像关系［12-13］，只需要3个对应点，就可以确定底片常数。首先采用三点拟合计算图像中心对应的天球坐标(α0，δ0)，利用该点的天球坐标计算得到导航星的理想坐标，即(αi，δi)到(ζi，ηi)：

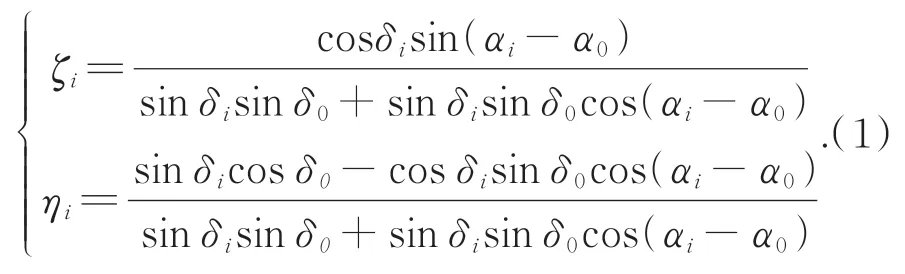
理想坐标实际上是空间星象的地心投影（Gnomonic Projection），其本质是针孔相机的成像关系，即带入较小畸变误差地模拟长焦望远镜。理想坐标将天球系统转化为笛卡尔平面坐标，得出了导航星在各帧不同的位置坐标。目标定位时，将其理想坐标(ζs，ηs)转换为天球坐标(αs，δs)的变换如式（2）：

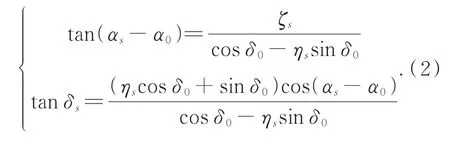
仅依靠3个点可能出现误匹配的情况，此外三点拟合精度也较低，因此必须对考察列表进行校验，并进行多点拟合。对于正确匹配，当图像x和y方向的比例尺相同时，恒星的理想坐标(ζi，ηi)和其度量坐标(xi，yi)应满足底片常数的对应关系，如公式（3）（当拍摄图像为镜像时，转换矩阵元素应为相应的下组符号）。通过该组关系可以判定匹配是否正确（T是否为酉矩阵［14］），并且将6底片常数减为3底片常数（a，b，θ）：

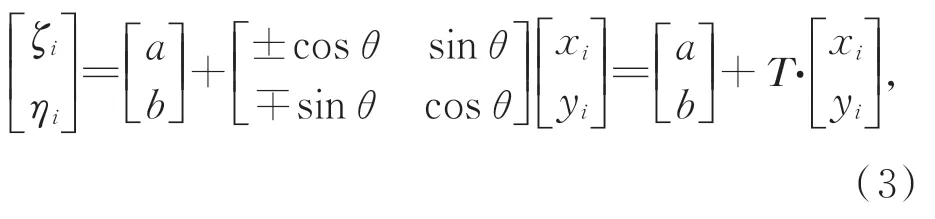
式中：a，b表示理想坐标系和度量坐标系间的平移量，θ表示两坐标系间的夹角。当已知一组(xi，yi)和其对应的(ζi，ηi)时，底片常数便可由最小二乘法得出。

3 算法构成

3.1 图像获取与预处理

本研究工作所有实际观测都依托于中国科学院国家天文台长春人造卫星观测站运维的1.2米口径地平式光电望远镜的主焦点［15］。该望远镜位于吉林省吉林市（图1）。望远镜动态峰值误差为方位轴：2.555″，高度轴：2.170″，为典型的精跟型望远镜。望远镜搭载的相机为Andor iKon-XL 230，4 096×4 108 pixel，像 素 尺 寸 为15 μm，视 场 约 为1.5°。望 远 镜 的 焦 距 约 为2.2 m。

图1 1.2米光电望远镜实物照片Fig.1 Photo of 1.2 m optical telescope of Changchun observatory

拍摄得到的图像如图2，应用SExtractor（Source-Extractor）软 件［16］进 行 星 象 质 心 位置的提取。之后采用静态特征和运动特征差异来初选疑似目标并通过连续帧关联确定目标。最后根据望远镜指向筛选Tycho-2星表，剔除双星并选出视星等介于8～10、自行小于10 mas/yr的恒星进行匹配。

图2 1.2米光电望远镜跟踪目标时拍摄的星空Fig.2 Image captured by the 1.2 m optical telescope when tracking a target

3.2 星表数据的资料归算

本研究采用Tycho-2恒星星表，该星表是建立于ICRS下的，历元为J2000.0。因此需将星表中的恒星坐标进行自行、周年视差、周年光行差和光线偏转的归算，解算到恒星在观测时刻的GCRS坐标进行星图匹配。本文应用ANCI C版本的SOFA（Standards Of Fundamental Astronomy，from IAU）软 件 包［17］中 的 程 序 做 以 上 的换算。

几点说明：基于望远镜拍摄图像的天文定位给出的是目标的站心空固坐标，由于恒星站心和地心间的周日视差可忽略，可采用恒星的GCRS坐标进行星图匹配。恒星由岁差—章动、极移引起视位置差别很小，不影响理论与观测星图的匹配。大气折射同时影响背景恒星和目标，精跟型观测中该较差可被忽略。

3.3 优化三角形匹配算法

本程序包括两部分算法：优化三角形匹配和序列图像修正。优化三角形匹配算法通过降维查表的方法提高运算速度，得到首帧的底片常数和较为精确的中心位置；该中心位置叠加码盘获得的望远镜指向改变量获得相应帧底片中心位置，并结合上一帧的底片常数进行新一轮的匹配。流程可见图3。底片常数可用来解算各像素对应的天球坐标。

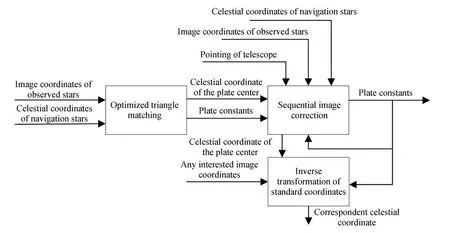
图3 本文所述快速星图匹配算法的程序框图Fig.3 Block diagram of the rapid star pattern recognition algorithm described in this work

本研究中三角形匹配算法利用“边-边-边”模式匹配观测星和导航星（如图4所示）。但是传统算法特征维数较低并且组构三角形过多，造成计算大量的冗余匹配，浪费计算时间和存储空间。

图4 三角形匹配的模拟示意图Fig.4 Simulation diagram of triangle matching

优化三角形匹配算法活动图如图5所示，观测端编号并计算每两颗星象之间的“边”——角距［18］，按照自然编号的顺序存储。经归算后星表中的导航星，编号并计算两两之间的角距，按照角距大小排列存储，称为排序导航星表。具有相同观测星的两个星对（例如观测星对：i，j和i，k），即为待测观测星对，分别放缩一定的误差σ后划取排序导航星表中的两个片段。判断这两个片段内是否存在共享导航星的两个星对，如果存在（例如导航星对：A，B和A，C），即为待选导航星对，计算这两个导航星对中不同导航星（即导航星B，C）间的角距。哈希查表（哈希函数如式（4），其中N为筛选星表中导航星数目）得到观测星对两相异星角距（即j，k之间角距），放缩该误差后所划定的导航星表范围，判断该范围是否包括对应相异导航星（即导航星B，C）的角距。是就将这些观测星和导航星按照对应关系放入待考察列表中（即i，j，k对应A，B，C）：

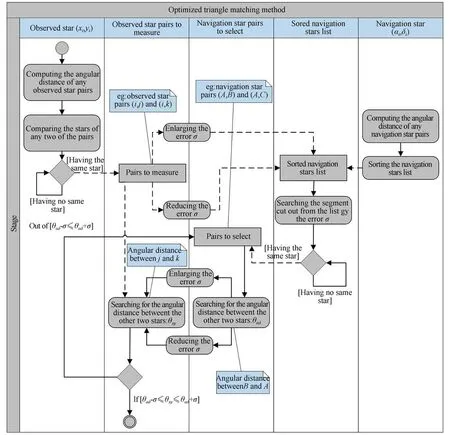
图5 优化的三角形匹配算法的活动图Fig.5 Activity diagram of the optimized triangle matching algorithm

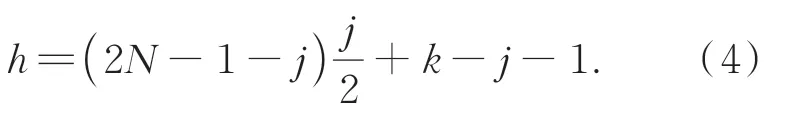
完成一组匹配后即得到粗略的定位关系，可求得图像中心对应的天球位置。该位置用来求得导航星的理想坐标，并将这组匹配进行参数拟合得到底片常数。用式（2）验证该底片常数，满足校验关系后进行观测星和导航星间的匹配，当有足够多匹配时，该底片常数方为正确。当无法得到正确匹配时，需要放大误差再次进行匹配，直到得到正确匹配或误差不可接受为止。放大误差后，导航星表范围增加，需屏蔽已考察的列表片段避免重复匹配，提高匹配效率。

3.4 序列图像修正算法

地心投影通过各帧图像中心将导航星绝对的天球坐标投影为本帧理想坐标；对于较高帧频的精跟型望远镜，帧间的底片常数变化很小，因此本帧理想坐标和上一帧参数可完成匹配。但是为了不引入累积误差，完成匹配后还需再一次的多点拟合修正底片常数。序列图像修正算法在不损失精度的前提下点对点地完成匹配，极大地节约存储空间，提高计算速度，这对于实时性解析目标位置有着重要意义。除此之外，对于大视场的望远系统，较多的背景恒星会造成三角形匹配中内存消耗过大、效率过低，对此可以根据望远镜指向筛选导航星并划取图像中心区域的观测星进行优化三角形匹配，再将得出的底片常数应用序列图像修正算法推广到整帧图像，进行底片常数计算。需要注意的是，这种情况下，常采用十二参数模型进行匹配，可以在一定程度上克服相机图像的畸变。序列图像修正算法流程如图6所示。

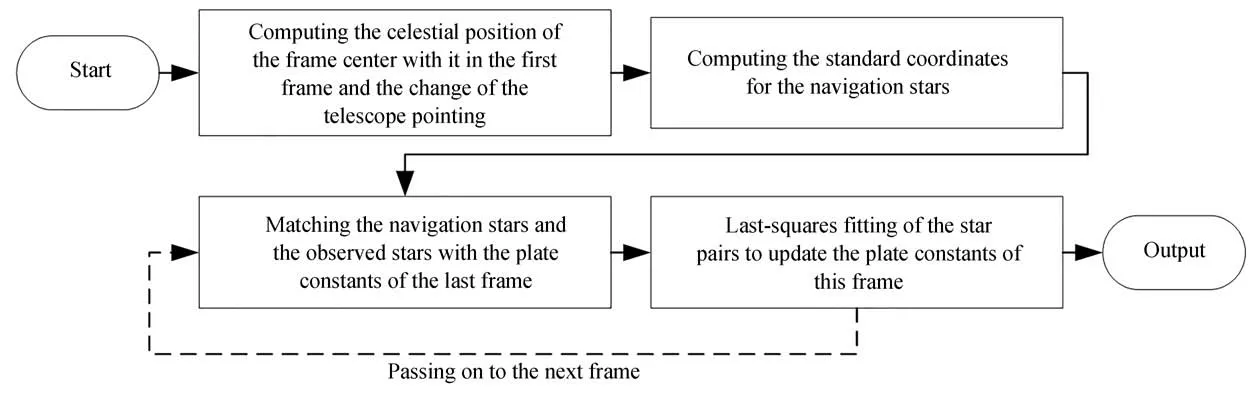
图6 序列图像修正算法流程图Fig.6 Flow chart of sequential image correction algorithm

望远镜码盘给出了其中心指向，但一些原因，如自然条件、热胀冷缩、配重变化、重力变形、结构改变（本例中望远镜可以调节主焦点和卡塞格林焦点）等会造成该指向不准；然而在同一圈次的观测中，指向的相对精度较高，因此配合首帧的修正中心就可以大幅提高底片的中心位置精度。该中心位置对恒星理想坐标运算和目标位置解算有着重要意义，同时还可对望远镜指向偏差提供参考。

4 实验结果

本研究采用Windows系统的计算平台，CPU：AMD Ryzen 5@3.4 GHz，内 存：8 GB DDR4，编译环境为VS 2019。

将优化算法和传统的三角形匹配算法作比较，对于39颗观测星对应39颗导航星的实验，传统算法耗时2.105 s，而优化算法耗时0.044 s。

将算法应用于精跟测试中轨激光星的事后分析中，观测时间为2019年4月，指向范围：（1 h30 m16.2 s，53°0′50.2″）～（2 h15 m13.0 s，50°33′40.0″）。首帧识别到326颗观测星，筛选出66颗导航星，首先对所有涉及的背景恒星进行了归算，共消耗时间0.005 s，后采用优化的三角形匹配算法对首帧数据进行匹配。经4次放大，理想坐标匹配误差为0.000 04时，可匹配60对星象，共需时间0.75 s。经最小二乘法拟合出底片和地平取向基本成镜像。匹配结果如图7，其中红圈表示成功匹配的星象（彩图见期刊电子版）。

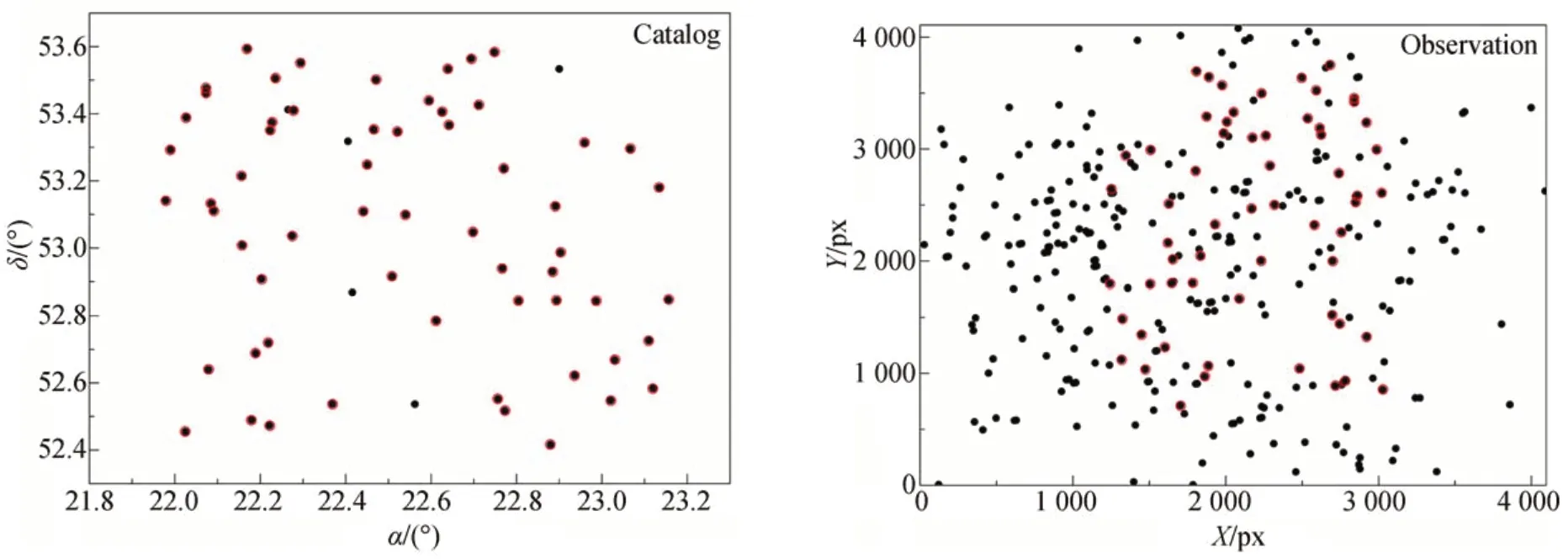
图7 观测星和导航星二维点图Fig.7 Two dimensional point maps of observation and navigation stars

对后续帧采用序列图像修正算法，将计算结果列于表1，可见该算法耗时均在0.04 s以内，在识别到充分多观测星时，可实现绝大多数导航星的匹配。

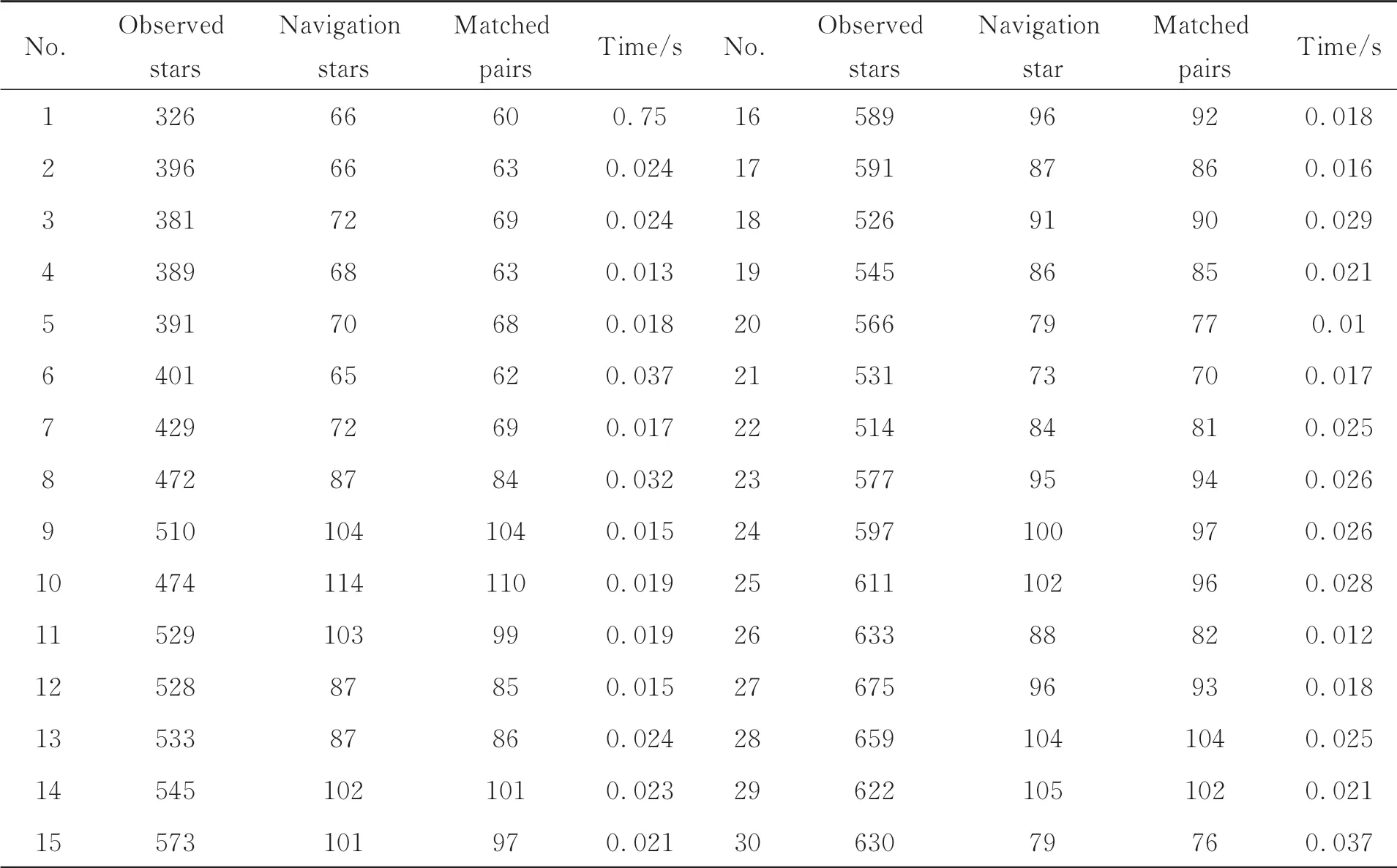
表1 序列星图匹配结果Tab.1 Results of sequential star pattern matching

匹配星对用于拟合，得出各帧的底片常数。底片常数的缓变是序列星图匹配算法的主要依据，30帧的常数（式（3）中a和b）变化如图8所示，可见常数变化较为均匀，可用线性回归来表示，其皮尔森相关系数均达到99.6%以上；并且经30帧，两参数均减小了不超过10%。

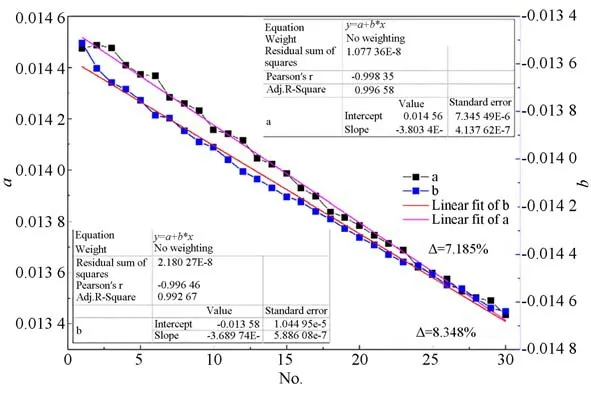
图8 序列星图匹配算法中底片常数a和b的变化Fig.8 Changes in the constants a and b in the sequential star pattern matching

由拟合的底片常数计算得出的观测星的天球位置和实际导航星之间的误差可由图9表示（彩图见期刊电子版），某一典型帧赤纬方向的误差由绿色球表示，赤经方向由红色方块表示。可见除个别边缘点外，绝大多数的星象误差在6角秒以内。由于精跟型拍摄目标多位于视场中心，其误差会进一步缩小，对于观测的中轨激光星，30帧的目标统计误差如图10所示。可以看出，除第一帧以外，绝大部分目标的误差在2″以内，所有帧的平均误差为=0.53''，=-0.34''。由此可证明本文所述方法的有效性。

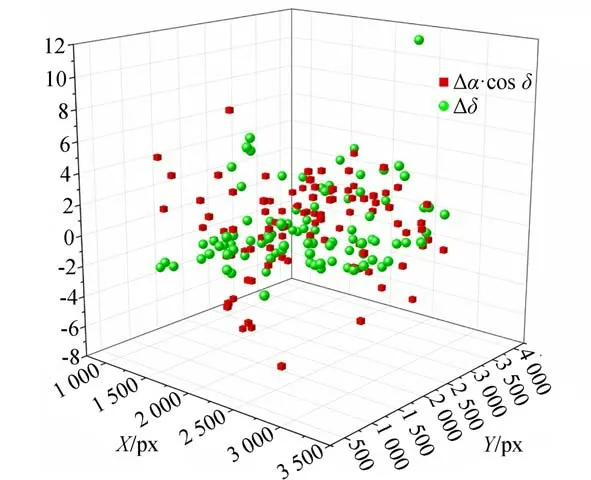
图9 某帧星图匹配采用底片常数计算观测星的天球位置和导航星的误差分析Fig.9 Error analysis of the celestial positions of the observation stars within the film constants calculation and the respondent navigation stars

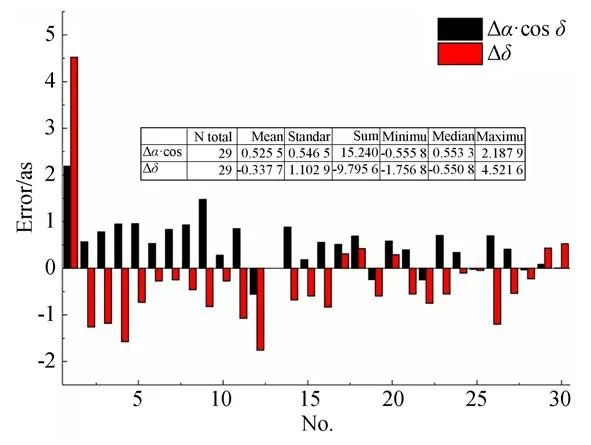
图10 30帧星图匹配用于目标天文定位的误差统计Fig.10 Error statistics of star pattern matching for the target celestial positioning in 30 frames

5 结论

本文所述的星图匹配程序包括基于降维查表优化的三角形匹配和基于上一帧底片常数的序列图像修正，该程序特别适用于精密跟踪型的大视场望远镜。其中优化三角形匹配算法相较于原始算法大幅提高了匹配速度（39颗观测星对应39颗导航星，时间从2.105 s降到0.044 s），而序列图像底片常数修正进一步加速，使得100颗左右的匹配星对在0.04 s以内完成，这说明了算法的高效性；本方法对中轨激光星定位的结果显示其平均误差为