基于机器学习的电力数据回归分析和预测技术研究
2022-11-28赵俊梅张利平任一峰
赵俊梅, 张利平, 刘 丹, 任一峰
(中北大学 电气与控制工程学院, 山西 太原 030051)
0 引 言
随着物联网、 大数据、 机器学习、 云计算等新型技术与电力系统的交叉融合, 可以更好地保障电力系统的安全运行、 资源优化配置、 产业和能源结构优化、 电力用户需求响应. 电力大数据的合理分析和精准预测对于电网系统的安全性、 经济性、 环保性、 稳定性和预见性具有非常重要而深远的意义. 电力大数据预测是电力行业研究的重要课题之一, 通过对海量的电力历史数据进行探索和分析, 不断寻找巨大数据变化和各种因素之间的内在规律, 可对未来进行预测和估计. 科学合理的数据分析和准确预测, 对于电力行业的发展战略、 运营稳步提升、 资源能源配置、 用户用电行为等均具有重要作用.
聚焦电力大数据分析和价值挖掘, 可以强化“电力看经济”“电力看环保”“电力看智慧”等社会服务能力, 助力国家遏制高耗能、 高排放、 低水平项目盲目发展, 朝着节约用电、 高效用电、 绿色用电的方向发展. 功率因数是电力系统中交流电路的重要参数之一, 它是衡量电气设备效率高低的重要标准和电力系统是否经济运行的重要指标. 随着光伏、 风电等新能源并网, 也给功率因数带来了影响. 文献[1-2]研究了光伏和风电对功率因数的影响. 文献[3]对无功负荷进行了分析和预测. 文献[4]研究了光伏发电的不确定性, 对电网质量带来的影响进行了分析. 文献[5]介绍了风电的间歇性和随机性, 给电网安全管理带来了挑战. 文献[6]利用回归模型预测功率因数, 重点针对电价的影响. 本文利用机器学习算法对发电厂的功率因数等数据进行回归分析和科学预测, 进而提高能源利用率.
1 支持向量机回归
支持向量机回归(Support Vector Machine Regression, SVMR)算法可以归结为求解一个凸二次规划问题, 理论上将获得全局最优解, 算法非常巧妙地解决了维数问题, 算法的复杂度与样本维数没有关系, 它是根据训练样本数据构造回归函数, 无需熟知回归函数结构的先验信息, 便可保证回归有较好的推广能力. 部分回归问题无法使用线性模型进行充分描述, 可利用拉格朗日对偶公式扩展到非线性函数[7-8]. 利用式(1)查找非线性回归需要的最小化系数

(1)
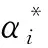
满足约束条件
式中:C为惩罚因子, 一般为正.
预测函数为

(2)
式中:b为偏差量.
Karush-Kuhn-Tucker (KKT)互补条件为
∀n:αn(ε+ξn-yn+f(xn))=0,
∀n:ξn(C-αn)=0,

(3)

2 高斯过程回归
高斯过程是正态随机过程, 是一种基于贝叶斯理论和统计学习理论的核学习机, 其模型是非参数的基于核的概率模型[9].
训练集为T={(xi,yi);i=1,2,…,n}, 式中xi∈Rd,yi∈R. 线性模型如下
y=xTβ+ε,ε=N(0,σ2),
(4)
式中:β为系数;ε为服从均值为0、 方差为σ2的噪声.
高斯过程回归(Gaussian Process Regression, GPR)是一组随机变量, 任意二者之间具有联合高斯分布[10], 潜在变量f(xi),i=1,2,…,n, 如果f(xi),x∈Rd, 则潜在变量f(x1),f(x2),…,f(xn)是联合高斯分布.响应变量可以创建以下模型

(5)
式中:h(x)为基函数;β为基函数系数.
由于高斯过程回归模型是一个概率模型, 故存在一个潜在变量对应一个观察值, 进而使高斯过程回归为非参数模型.
模型相当于
P(y|f,X)~N(y|Hβ+f,σ2I),
(6)
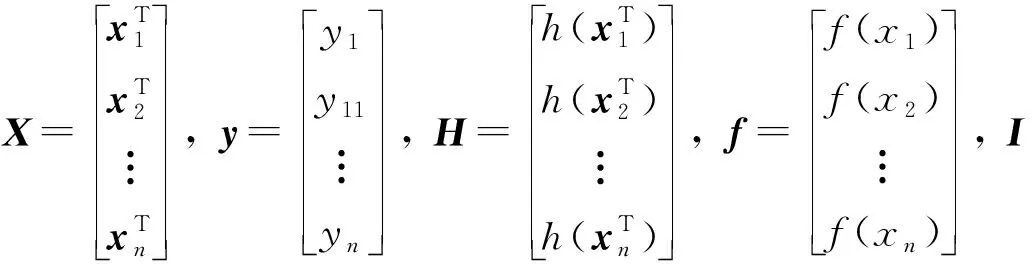
3 CART决策回归树算法
分类与回归树(Classification and Regression Tree, CART)算法是通过由测试变量和目标变量构成的训练数据集的循环分析而形成二叉树的结构[11]. 由CART算法生成一棵深度的决策树, 利用贪心策略来搜索近似最优均方误差[12]. 节点分割的主要步骤如下:
3) 接着按照升序对预测值xi进行排序.分类回归预测器的每个元素都是分裂候选、 切割点.算法记录与未分裂集合TU中的缺失值相对应的所有索引.
4) 通过最大化所有分裂候选的均方误差的减少来确定使用xi分裂节点t的最佳方式.决策树将节点t中的观察结果分成左右两个子节点.
5) 在最大化均方误差减少的切割点分割预测变量.
回归树通过使用均方误差(MSE)对叶子进行修剪, 算法合并来自相同父节点的叶子, 此父节点的MSE最多是其两个子节点的MSE之和. 回归树拆分当前层的所有节点, 然后统计分支节点的数量.
4 超参数优化
在机器学习选择模型的过程中, 需要通过灵活调整超参数进而改变模型复杂度, 挑选出其中最优的超参数组合, 使模型具有更好的学习效果和性能.
超参数优化(Hyperparameter Optimization, HO)可大大提高模型在独立数据集上的优势和性能, 通过超参数的不同组合, 最终最小化模型均方误差. 一般使用交叉验证来评估不同超参数下的模型泛化性能, 故常常采用超参数空间中交叉验证值最优的超参数作为最优超参数, 模型构建的参数一般都可以采用此方式进行优化[13]. 通常, 选取最小化五倍交叉验证. 但是, 在优化过程中, 通过超参数优化需要防止过度拟合.
支持向量机回归可以对核函数、 框约束、 内核规模等参数进行优化. 核函数决定在训练SVM之前应用于数据的非线性变换, 一般可以选择高斯或者径向基函数. 框约束控制着对具有较大残差的观测值施加的惩罚, 约束值越大模型更灵活. 反之, 约束值越小, 模型越刚性, 对过度拟合越不敏感. 内核规模可以控制核发生显著变化的预测因子的比例, 较小的内核规模提供了更灵活的模型. 高斯过程回归可以对基函数、 核函数、 内核规模、 Sigma等参数进行优化. 基函数指定高斯过程回归模型的先验均值函数的具体形式, 一般可以选择零、 常数、 线性. 而核函数是将响应中的相关性确定为预测值之间距离的函数, 一般是平方指数、 Matern 5/2、 Matern 3/2和指数等. Sigma用于设定观测噪声标准差的初始值. 回归树主要对最小叶子尺寸参数进行优化. 最小叶大小设定是用于计算每个叶节点响应的最小训练样本数.
5 仿真分析

下面列出实际仿真实验的几种主要情况. 支持向量机回归采取内核比例分别为sqrt(p)/4和sqrt(p)的高斯核的两种情况,p为预测变量的数量, 核函数均为高斯函数, 核尺寸分别为4.3和1.7. 高斯过程回归采取核函数分别为高斯回归指数、 Mastern 5/2的两种情况, 基函数设置为常量, Sigma设置为自动模式. 若回归树CART树最小叶子大小为4, 则认为是精细树, 若最小叶子大小为12, 则认为是中等树. 下面利用这些回归算法对电力数据进行回归分析, 主要从RMSE、R2、 MSE、 MAE、 Time角度进行比较分析. RMSE为均方根误差;R2为拟合系数, 定义为R2=1-SSE/SST, SSE和SST分别为残差平方和、 总平方和; MSE 为均方误差; MAE为平均绝对误差; Time为运行时间.
SVMR1和 SVMR2分别为两种高斯核的结果, GPR1和GPR2分别为两种高斯过程回归的结果, CART1和CART2分别为回归树的结果. 具体结果如表 1 所示, 通过观察几种误差、 拟合系数和运行时间的参数, SVM的R2最小, GPR的运行时间比较长, CART的误差较小, 故可以看出CART1也就是精细树的回归结果最好.

表 1 三种机器学习算法的回归结果Tab.1 Regression results of three machine learning algorithms
本文针对3种回归算法通过超参数优化比较和分析其回归效果. 支持向量机的优化器为贝叶斯优化时, 核函数为线性, 框约束和核尺寸为自动模式. 优化的超参数中框约束为 0.002 06, 核函数为三次, Epsilon值为0.011 3. 优化后的超参数中框约束为 0.001 09, Epsilon值为 0.000 029 2. 高斯过程回归优化器为贝叶斯优化, 基函数为常量, 核函数为各向同性指数. 优化后的超参数中基函数为零, Sigma值为0.055 5. 回归树优化器为贝叶斯优化, 可以设置最小叶子大小为1. 优化后的最小叶大小为5. 3个算法的超参数优化迭代次数均设置为30, 综合误差回归树最小, 运行时间回归树最快, 综合回归效果回归树较好.
同时, 为了寻找回归树最优的优化器, 先将回归树优化器调整为网格搜索, 设置最小叶子大小为5, 网格分区数量为10, 优化后最小叶大小为6, 运行时间只有4 s多, 误差更小. 再把优化器调整为随机搜索时, 设置最小叶子大小为6, 迭代次数为30, 优化后最小叶大小为5, 但是相对网格搜索迭代次数多了不少, 运行时间也增加到12 s多.
SVMRHO 和GPRHO分布为支持向量机回归超参数优化和高斯过程超参数优化的结果. CARTHO1 、 CARTHO2、 CARTHO3分别为回归树贝叶斯优化、 网格搜索、 随机搜索的优化结果. 5种超参数优化的仿真结果误差及运行时间如表 2 所示. 综合考虑拟合系数、 误差大小和运行时间, 基于网格搜索优化器的回归树的效果最好, 故最终选用其作为对验证集数据进行仿真实验.
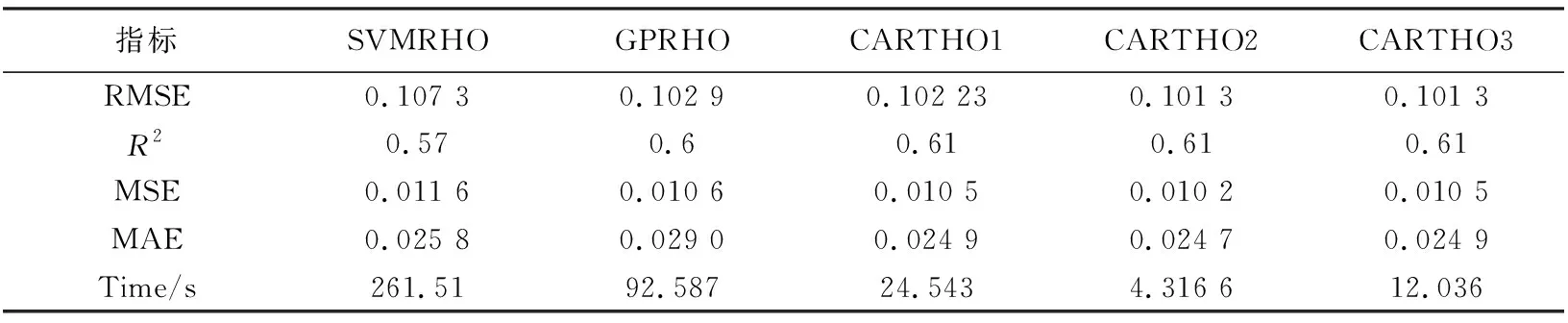
表 2 三种机器学习算法经超参数优化的结果Tab.2 Hyperparametric optimization results of three machine learning algorithms
为了验证回归模型的预测性能, 通过验证数据对模型进行验证测试. 选取5天的功率因数进行比较和分析. 表 3 列出5天真实数据和回归模型预测数据及二者之间的差值.

表 3 5天真实和预测功率因数及误差的情况表Tab.3 5-day actual and predicted power factors and errors
图 1 是优化器为网格搜索的回归树的超参数优化后的响应图, 它显示了响应和记录编号的关系, 也可以反应真实值和预测值之间的关系. 图 2 是优化器为网格搜索的回归树的超参数优化后的最小MSE图. 图中可以看到最佳点超参数和最小误差超参数, 每个黑色点对应于由优化过程计算的最小MSE的估计值. 通过分析, 优化器为网格搜索的回归树的回归效果良好.
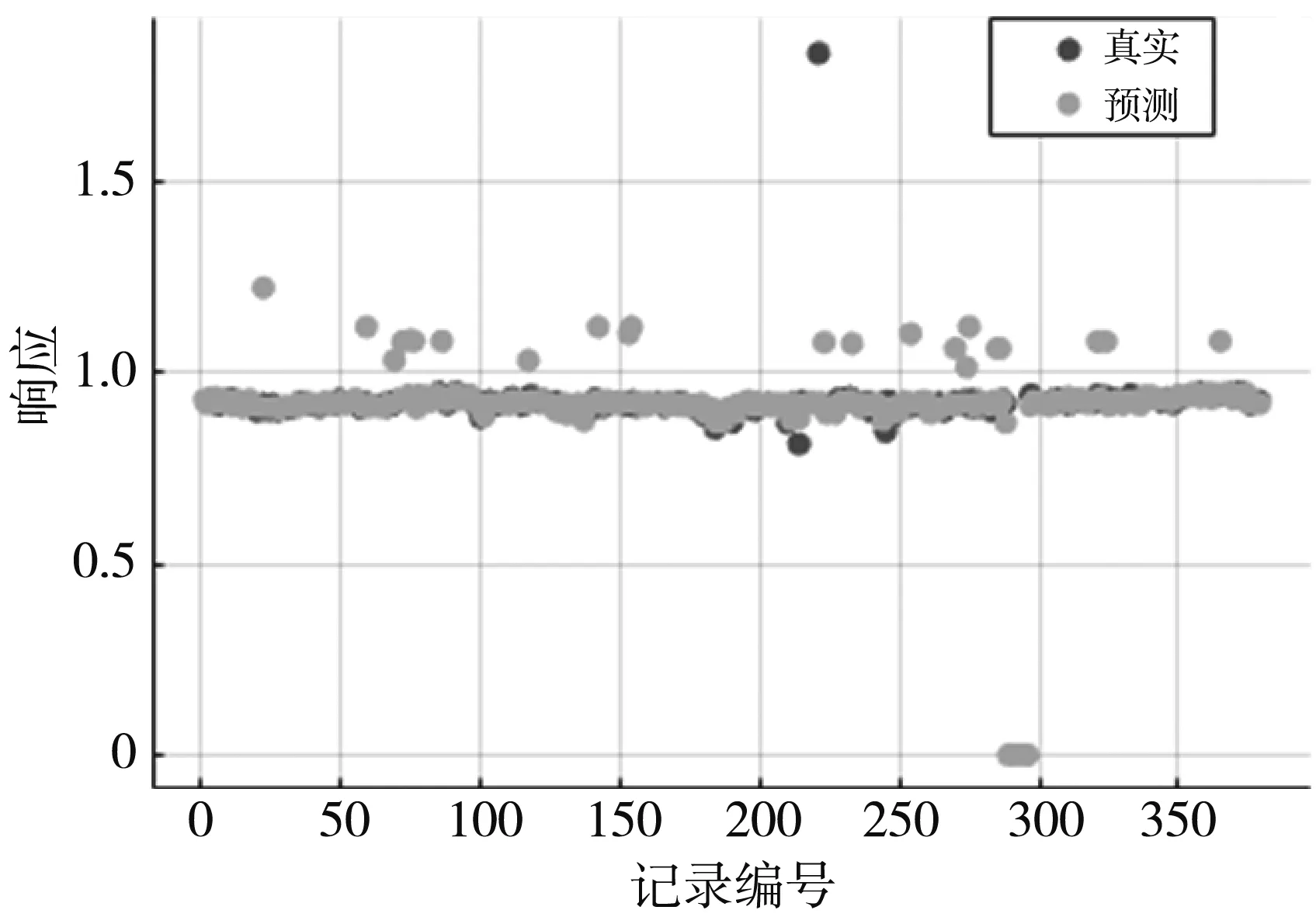
图 1 回归树的响应图Fig.1 Response graph of regression tree

图 2 回归树的最小MSE图Fig.2 Minimum MSE graph of regression tree
6 结 论
机器学习的成熟和发展为电力大数据的分析提供了丰富的算法. 通过机器学习算法对电力数据进行科学分析和深入研究, 可以发现、 寻找和探究数据之间的相关性、 规律性, 并创建和训练模型, 做出合理的预测和估计, 最终保障电力系统节能管理和绿色持续发展. 回归分析是机器学习中的经典算法之一, 本文介绍了支持向量机回归、 高斯过程回归、 回归树CART 3种算法的基本原理, 并利用算法对某电厂的电力数据进行分析和比较. 同时, 还利用不同超参数优化算法对3种算法进行优化. 通过比较均方根误差、 拟合系数、 均方误差、 平均绝对误差、 运行时间等5个指标, 获得最优回归模型, 对实际电力数据进行了验证. 通过不同参数的多次仿真实验, 比较和分析了回归算法的优劣点, 证明了CART回归模型尤其是网格搜索优化后的效果较好, 并对今后的电力大数据预测和估计具有一定的现实意义.
