轻度抑郁症脑电特征分析与机器识别研究

尚照岩， 乔晓艳

(山西大学 物理电子工程学院， 山西 太原 030006)

0 引 言

世界卫生组织数据显示， 抑郁症已经影响了大约3.5亿人， 是全世界最严重的疾病之一. 抑郁症患者会出现持续的情绪低落， 沉浸于悲观心境， 甚至可能自杀. 抑郁症及时筛查和诊断是非常重要的， 探索一种抑郁症的机器识别方法有重要的应用价值和现实意义[1].

脑电(Electroencephalogram， EEG)作为一种客观可靠的抑郁评估手段， 具有较高的时间分辨率、 相对低成本、 易记录且对患者身体无任何侵入式伤害等优点， 越来越多的学者开始使用脑电数据建立机器学习模型对抑郁症和正常人进行识别[2-4]. Yang等[5]采集5 min静息态EEG数据， 采用单一时间窗口对脑电beta节律数据进行处理， 提取了线性和非线性特征， 使用机器学习算法对 beta 节律脑电特征在不同导联下进行分类， 准确率依次为导联 FP1(76.41%)， O2(75.23%)， F3(75.12%)， C3(74.29%). 由于该方法仅使用了单一时间窗口和单一的beta节律脑电数据， 没有选择最佳时间窗口， 未考虑alpha、 theta和gamma节律蕴含不同的脑电信息， 因此， 单导联分类准确率较低. 文献[6-7]等人提取了30名中重度抑郁症患者和17名正常对照的单导联静息态脑电的8个线性特征， 使用GreedyStepwise特征搜索和k近邻分类算法对单导联进行分类， 对于 alpha 节律的静息态脑电数据， 可以实现 80.85%的分类准确率， 其电极分布在颞区； 对于 beta 节律的脑电数据， 最高分类准确率为 78.72%， 电极分布在颞区和顶区； 对于 theta 波段的脑电数据， 可获得 80.85%的最高分类结果， 其电极分布在前额区. 该文对不同节律的单导联分别进行分类， 得到每个脑电节律的分类准确率以及脑区位置， 该方法没有利用脑电的非线性特征， 没有对脑电进行有效分段， 导致分类准确率较低. Li等[8-9]以6 s时间窗对脑电数据分段， 提取出8个线性特征和9个非线性特征， 并使用K近邻分类算法对轻度抑郁患者和正常人的脑电特征分类， 单个导联分类结果依次为： O2(82.88%)、 F4(81.84%)、 T4(80.54%)、 C4(80.15%)， 该研究提取的17个脑电特征与抑郁症的关联性有冗余， 抑郁识别正确率还有待提高. 现有的研究还没有给出与轻度抑郁症密切相关的最佳脑电导联以及最有效的脑电特征组合， 且抑郁识别最佳的脑电时间窗口也不明确， 这些因素导致轻度抑郁症机器识别准确率有待提高. 因此， 本文从53名被试的16导联静息脑电数据中， 分别提取与抑郁情绪密切相关的脑电时域、 频域、 时频非线性特征， 利用随机森林、 K近邻以及支持向量机3种机器学习分类器进行抑郁脑电识别， 并对脑电时间窗口、 导联组合、 特征组合以及节律组合进行分析， 探索静息态脑电抑郁症机器识别的最有效方式， 提高轻度抑郁症分类正确率和识别效率， 为临床诊断抑郁症提供有效支持.

1 数据集与脑电预处理

1.1 抑郁脑电数据集

本文采用的数据集是兰州大学普适感知与智能系统实验室公开的轻度抑郁症数据集[10]. 所有的抑郁障碍患者是从兰州大学第二附属医院住院和门诊患者中招募的， 并且由至少一名临床精神科医生诊断， 正常对照是通过海报招募的， 得到兰州大学第二附属医院伦理委员会批准， 并在实验开始前获得了所有被试的书面知情同意. 所有抑郁症患者都接受了一个结构化的迷你国际神经精神病学访谈(MINI)， 该访谈符合基于DSM-IV的精神疾病诊断和统计手册(DSM)中的主要抑郁症诊断标准. 对于抑郁症患者， 纳入标准为MINI符合抑郁症诊断标准， 患者健康问卷PHQ-9评分大于或等于5分， 近两周未进行精神药物治疗. 排除抑郁症中有严重身体疾病和自杀倾向的患者， 并且排除正常对照中有精神障碍的被试或有精神障碍家族史的被试.

该数据集包含53个被试的静息态脑电数据， 其中包括24名轻度抑郁症患者(13名男性和11名女性， 年龄为16岁～56岁)， 以及29名健康对照者(20名男性和9名女性， 年龄为18岁～55岁). 脑电信号记录采用128导联的HydroCel Geodesic Sensor Net (Electrical Geodesics Inc., Oregon Eugene, USA)和Net Station(版本为4.5.4)采集软件， 采样频率为250 Hz， 参考电极为Cz导联. 在静息态脑电数据采集时， 首先对被试的头围进行测量， 然后根据头围选择合适的脑电帽. 记录数据之前对各个电极的阻抗进行测量， 确保接触良好， 并保持在50 kΩ以下. 在安静、 隔音、 无强电磁干扰、 通风良好的房间内对脑电信号进行测量. 记录了所有被试5 min闭眼静息状态的脑电数据. 实验过程中要求被试保持清醒和静止， 没有任何身体活动， 以及任何不必要的眼睛移动、 扫视和眨眼. 因此， 数据集中包含有53名被试、 128导联的5 min静息态脑电数据， 并且该数据集进行了眼电伪迹的去除.

1.2 脑电数据预处理

本文选择与情绪相关联的16个脑电导联进行研究[11]， 对应导联电极分别为： FP2、 FP1、 F3、 F7、 C3、 T3、 P3、 T5、 O1、 O2、 P4、 T6、 C4、 T4、 F8、 F4. 预处理采用MATLAB软件的EEGlab工具箱完成. 步骤为：

1) 电极重参考： 选用Cz为参考电极， 以其他电极与Cz电极之间的电势差为该电极的数据.

2) 滤波： 设置高通和低通滤波器对信号进行滤波， 高通滤波器截止频率设置为0.5 Hz， 低通滤波器截止频率为45 Hz. 目的是滤除工频干扰、 高频噪声、 直流漂移以及肌电伪迹. 滤波之后的脑电信号(仅示出1 s片段)如图 1 所示.

图 1 滤波之后的脑电信号片段Fig.1 EEG segment after filtering

3) 数据分段： 每个被试的脑电采集时间是5 min， 为了避免采集开始和结束对脑电记录的影响， 去除开始和结束各30 s的数据， 将剩余4 min脑电数据(采样点数为4×60×250)以不同时间窗口长度(8 s、 10 s、 12 s、 15 s、 20 s、 24 s、 30 s)划分数据片段， 用以选择脑电数据最佳的窗口时间.

4) 获取脑电节律： 对脑电数据片段设置带通滤波器截止频率， 获取theta(4 Hz～8 Hz)、 alpha(8 Hz～13 Hz)、 beta(13 Hz～30 Hz)和gamma(31 Hz～45 Hz)4个不同频段的脑电节律.

若选用20 s的时间窗口， 对于每一个导联， 每名被试有12个脑电数据片段. 数据集中， 24名抑郁症患者共有288(12×24)个抑郁脑电数据片段， 29名正常人共有348(12×29)个正常脑电数据片段. 若选取16个导联， 则共有288×16个抑郁脑电数据片段和348×16个正常脑电数据片段.

2 脑电特征提取

2.1 时域特征提取

活动性、 移动性、 复杂度是Hjorth定义的3个参数， 活动性和移动性可用于检查信号震荡程度， 是定量评估非平稳脑电信号的重要指标[12]. 复杂度是脑电活动非线性评估参数， 它反映了脑电信号的复杂混沌程度[13].

活动性定义为

(1)

式中：y(t)为脑电信号；μ为信号的均值，i=1,2,3，…,N， 脑电数据片段的样本数量； var表示方差. 对抑郁患者和正常被试， 各取288个脑电信号片段， 利用式(1)计算16个导联的脑电活动性. 其中， 在O1导联抑郁脑电和正常脑电的活动性如图 2 所示.

图 2 O1导联脑电活动性对比图Fig.2 Contrast map of EEG activity in lead O1

移动性定义为

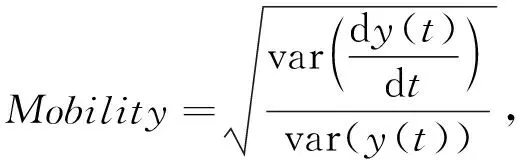
(2)

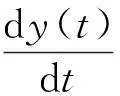
复杂度定义为

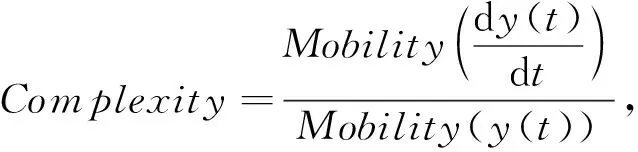
(3)

式中:Mobility为移动性. 对抑郁患者和正常被试， 各取288个脑电信号片段， 按照式(3)计算16个导联的脑电复杂度， 其中在O1导联抑郁脑电和正常脑电的复杂度如图 4 所示.

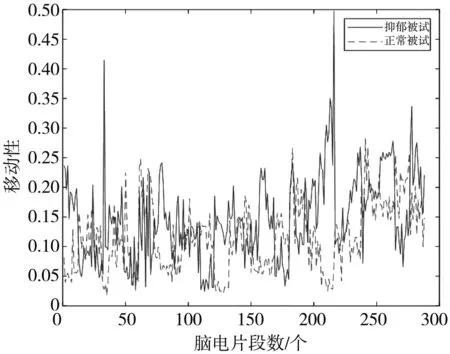
图 3 O1导联脑电移动性对比图Fig.3 Contrast chart of lead O1 EEG mobility

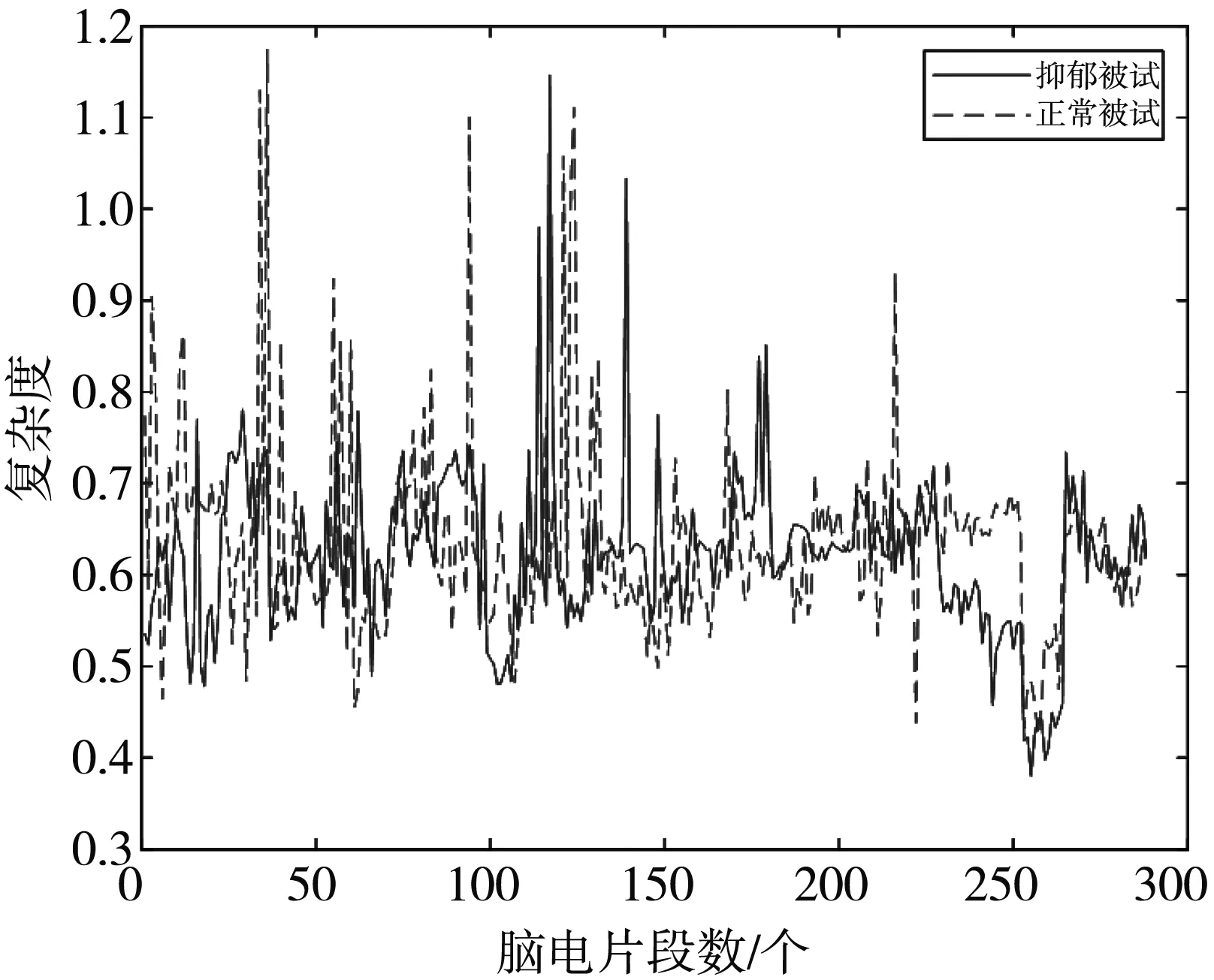
图 4 O1导联脑电复杂度对比图Fig.4 Contrast chart of EEG complexity of lead O1

2.2 频域特征提取

由于脑电信号是随机信号， 本文采用AR(Auto Regressive)模型方法计算功率谱密度(Power Spectrum Density， PSD)[14]， 计算公式为

(4)

图 5 O1导联脑电最大功率谱密度值对比图Fig.5 The comparison chart of the maximum power spectral density value of lead O1 EEG

2.3 时频非线性特征提取

小波变换可以将脑电信号分成不同的子带， 每个子带内小波系数的模按尺度函数累加形成小波能量， 每个子带内的小波系数反映了信号的能量分布. 系数较大者携带的信号能量较多， 反之， 能量较少. 熵表示信号的不确定程度， 小波能量熵采用小波变换在不同尺度的能量分布代替信号的概率分布， 小波能量熵计算公式为

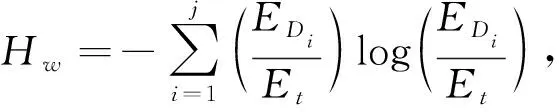
(5)

式中：i=1,2,…,j， 为小波分解的层数；EDi为第i层分解的小波细节系数能量；Et为小波总能量.

小波奇异熵是小波变换、 奇异值分解和信息熵的结合， 可以对被分解信号的突变程度给出确定的度量. 因此， 小波奇异熵可以区分具有不同时频分布的信号. 小波奇异熵计算公式为

(6)

式中：φj，φi为奇异值分解后对角矩阵上的奇异值. 对脑电信号的小波系数进行奇异值分解， 得到的对角矩阵能反映脑电信号的时频分布特征. 考虑到特征奇异值的个数有很多， 因此， 取前k(1≤k≤ρ)个奇异值以保证计算的精确性.

对抑郁患者和正常被试， 各取288个脑电信号片段， 利用式(5)和式(6)分别计算16个导联的脑电小波能量熵和小波奇异熵， 其中在O1导联抑郁脑电和正常脑电的小波能量熵和小波奇异熵结果如图 6 所示.

(a) 小波能量熵对比图

3 抑郁脑电分类算法与实现

3.1 输入特征集

为了对比不同机器学习方法对轻度抑郁症脑电识别的有效性， 使用单导联全频段脑电的归一化数据特征作为输入集， 输入特征矩阵为636×6. 其中， 636为单导联的脑电片段样本数量， 6为上节中提取的脑电6个特征量(特征维数). 将输入特征集分为训练集和测试集， 其中训练集特征矩阵为445×6， 测试集特征矩阵为191×6.

3.2 分类器简介

K近邻(K-Nearest Neighbor， KNN)是一种用于解决分类和回归问题的有监督的机器学习算法. 在传统机器学习算法中， 它是简单、 有效、 易于实现的算法之一. 在特征空间中， 如果一个样本最近邻的K个样本的大多数属于某一个类别， 则该样本也属于这个类别.K值范围在1～30之间， 使用网格搜索算法进行参数调整， 得到的最佳取值是1.

支持向量机(Support Vector Machines, SVM)是建立在统计学理论结构风险最小原理基础上的， 能较好地解决小样本、 非线性、 高维数和局部极小点等问题， 具有求解速度快、 泛化能力强的优点. 本文对不同核函数的SVM进行对比分析， 选择核函数为高斯径向基的SVM. 在SVM的参数中， gamma参数显示了训练示例的影响范围， 高值通常表示为“近”， 低值表示为“远”. 参数c表示正则化， 根据决策函数的边际最大化来纠正训练样本的分类. 一般， gamma在-5～1之间进行取值，c在0.01～50之间进行取值， 本文使用网格搜索算法进行参数调整， 得到gamma的最佳取值为0.212，c的最佳取值为19.7.

随机森林(Random Forest, RF)是具有代表性的Bagging集成算法， 由决策树组成随机森林评估器. 装袋法的核心是构建多个相互独立的评估器， 然后对其预测进行表决来判定集成评估器的结果. 随机森林考虑多个决策树的建模结果， 得到一个综合评判， 以此来获取比单个模型更好的回归或分类表现. 本文采用网格搜索进行决策树的数量、 最大深度、 最小样本个数以及最小分裂样本个数调整， 得到决策树个数为17、 最大深度为11、 最小样本个数为1以及最小分裂样本个数为2.

3.3 评价指标

分类问题常用的模型评价指标为分类准确率(Accuracy, Acc)、 精确率(Precision, P)、 召回率(Recall, R)和F1值. 其中，F1值可以反映精确率和召回率.F1值越大， 表明分类器泛化性能越好.

分类准确率为

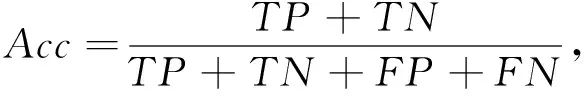
(7)

精确率为

(8)

召回率为

(9)

F1值为

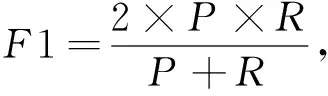
(10)

式中：TP表示将正类预测为正类数， 即真正类；FN表示将正类预测为负类数， 即假负类；FP表示将负类预测为正类数， 即假正类；TN表示将负类预测为负类数， 即真负类.

4 仿真结果与分析

4.1 分类器结果对比

将提取到的脑电信号时域特征、 频域特征、 非线性特征， 采用KNN、 SVM和RF算法对每个脑电导联的输入特征集进行分类， 得到高斯径向基SVM的分类结果优于其他2个分类方法. 导联O1在SVM、 KNN、 RF分类器上的混淆矩阵如图 7 所示， 并利用式(7)～式(10)计算其分类准确率Acc、 精确率P、 召回率R和F1值.

由图 7 可知， 采用SVM方法进行轻度抑郁症脑电分类， 单导联O1得到的识别准确率为84.3%，F1值为0.833； KNN方法得到分类准确率79.6%，F1值为0.806； RF方法获得的识别准确率为80.1%，F1值为0.815. 由此可见， SVM方法对轻度抑郁脑电进行分类， 其识别正确率和泛化能力均比KNN方法和RF方法好， 也较文献中采用相同抑郁脑电数据集的识别准确率高. 因此， 在结果分析时， 采用了SVM分类器.

4.2 不同脑电节律对抑郁症分类结果的影响

在抑郁症临床诊断中， 脑电节律信息可作为识别抑郁症的有效生物标记物. 本文对脑电theta、 alpha、 beta和gamma节律分别提取了6个特征， 构成特征集. 针对不同的输入特征， 在导联O1、 O2、 T5的分类结果如表 1 所示.

表 1 不同特征组合的支持向量机分类准确率Tab.1 Support vector machine classification accuracy for different feature combinations

由表 1 可知， 在4个单一脑电节律中， beta节律取得了最高的分类准确率， 可知脑电β节律与抑郁情绪更相关. 采用alpha， beta， gamma 3个节律组合， 在绝大多数的脑电导联都获得了最好的分类准确率. 采用多个脑电节律组合进行轻度抑郁症识别相比单一的脑电节律， 识别准确率提高了13%； 相比全频段脑电， 识别平均准确率提高了9%. 由此可见， 对于静息态抑郁脑电的机器识别， 选用脑电alpha， beta， gamma节律组合更有效.

4.3 不同导联选择对抑郁识别结果的影响

使用SVM分类器对16个脑电单导联一一进行抑郁分类， 单导联的分类准确率如图 8 所示.

图 8 单导联的分类准确率Fig.8 Single-lead classification accuracy

由图 8 可知， 导联T5取得最高的分类准确率89.53%， 导联C4取得最低的分类准确率 76.44%. 由于大脑是一个复杂的系统， 为探索适合轻度抑郁症识别的最佳导联组合， 本文选择分类准确率较高的单导联 O1、 O2、 T5进行组合， 按照分类准确率进行对应导联组合， 得到3种不同组合方式的抑郁脑电分类性能评价， 如表 2 所示.

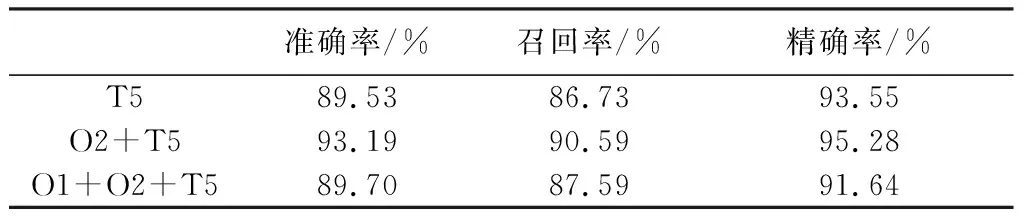
表 2 不同导联组合的分类性能评价Tab.2 Classification performance evaluation of different lead combinations

由表 2 可知： 在导联O2和T5组合下， 可以取得最高的分类准确率93.19%、 召回率90.59%和精确度95.28%， 因此， O2+T5可作为轻度抑郁识别的最有效的脑电导联组合. 由于本方法仅依靠这两个导联的脑电信息即可获得较高的识别准确率， 故而为抑郁症机器筛查探索出了一种最佳的脑电导联选择方式， 取得了优于其他导联输入方式的抑郁识别正确率.

4.4 脑电不同时间窗口选择对分类结果的影响

选用不同的时间窗口对原始测量的脑电信号进行分段， 不同大小的时间窗口对抑郁脑电识别结果产生影响， 为了找到轻度抑郁症识别的最佳时间窗口， 按照不同时间窗口分别对O1、 O2、 T5导联的原始脑电数据分段并提取特征， 得到抑郁脑电分类结果如表 3 所示.

表 3 不同时间窗口的分类准确率Tab.3 Classification accuracy for different time windows

由表 3 可知： 在8 s时间窗口， 导联O1、 O2、 T5均取得了较低的分类准确率； 在20 s时间窗口， 导联O1、 O2、 T5取得了最高的分类准确率. 之后随着窗口时间的增加， 分类准确率下降. 这是因为时间窗口较小时， 截取脑电片段所包含的抑郁信息不够充分； 时间窗口过大时， 脑电信息产生相互冗余导致分类正确率降低. 因此， 对于轻度抑郁症脑电进行机器识别， 20 s时间窗口是最佳的脑电分类时间窗口.

4.5 不同脑电特征对郁郁症分类结果的影响

选取alpha、 beta和gamma节律组合、 O2+T5导联组合、 20 s时间窗口， 利用支持向量机方法对脑电单个特征一一进行分类， 单特征分类正确率如图 9 所示.

由图 9 可知， 脑电活动性特征取得了84.56% 的单特征分类准确率， 可作为识别抑郁症的有效生物标记物. 小波能量熵和小波奇异熵两个非线性特征的分类准确率适中， 可以对轻度抑郁症患者和正常被试的脑电数据进行较好的区分. 依据单特征分类准确率的排序， 对脑电不同特征进行组合， 组合2表示活动性+移动性， 组合3表示活动性+移动性+小波能量熵， 其余依次类推. 分别对这些特征组合采用支持向量机进行分类， 其准确率、 召回率、 精确度如图 10 所示.

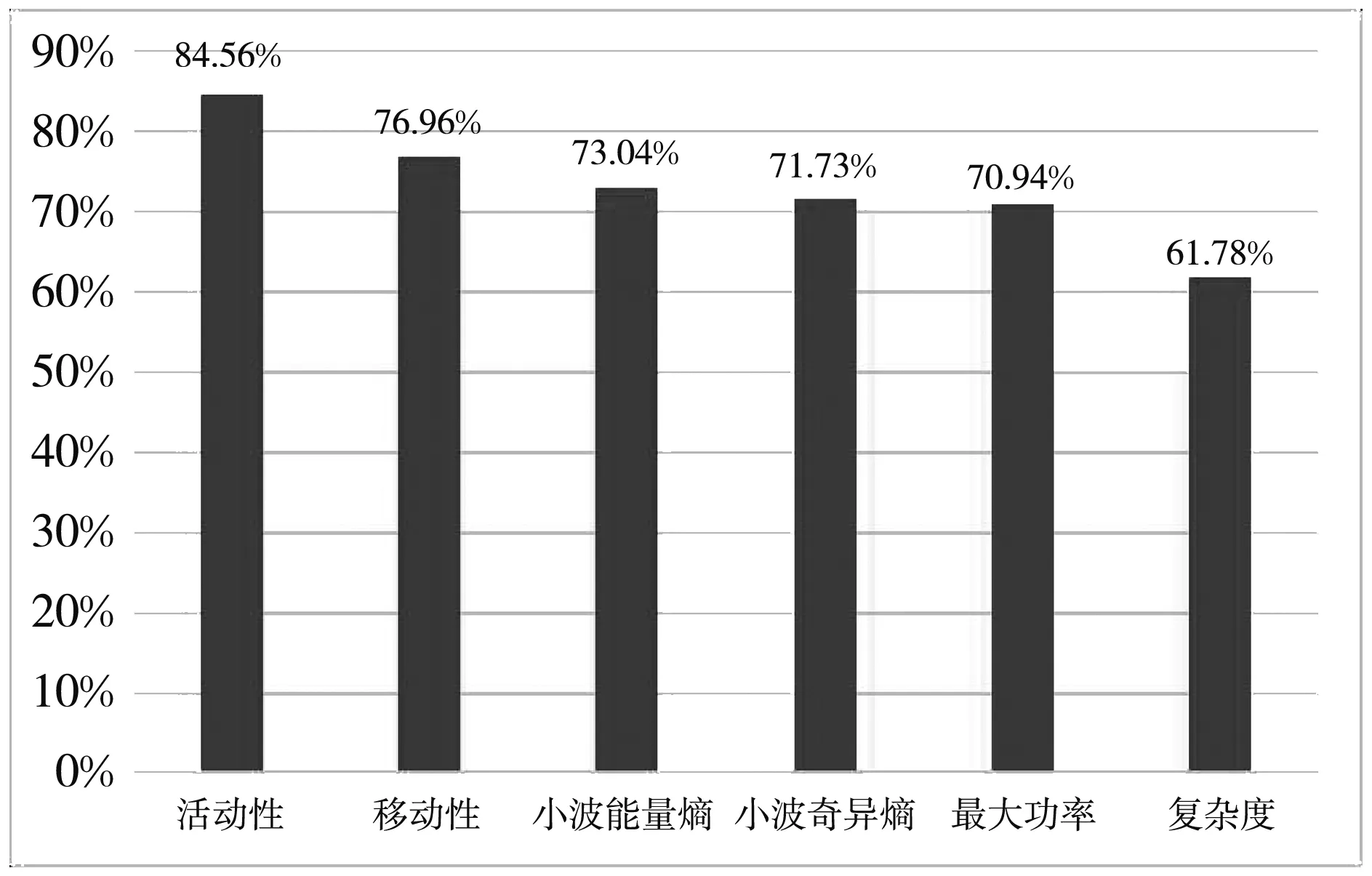
图 9 单特征分类准确率Fig.9 Single feature classification accuracy

图 10 不同特征组合的支持向量机分类结果Fig.10 Support vector machine classification results for different feature combinations

由图 10 可知， 将活跃度、 移动性、 小波能量熵、 小波奇异熵4个特征进行组合时， 取得最高的分类准确率94.24%、 召回率92.35%、 精确度96.23%. 由于活动性和移动性反映了脑电的震荡性， 熵反映脑电的非线性不确定度， 表明脑电的非平稳震荡特性与轻度抑郁症关系更密切， 脑电非线性与轻度抑郁的关系次之. 此外， 随着脑电特征组合数量的增加， 分类准确率降低， 表明特征之间存在冗余， 并非特征越多越好.

5 结束语

本文提取了脑电活跃度、 移动性、 复杂度、 功率谱密度、 小波能量熵、 小波奇异熵特征， 使用SVM、 KNN、 RF机器学习方法进行静息态抑郁脑电分类. 通过对脑电最佳时间窗口、 导联组合、 特征组合、 不同节律组合的分析， 探寻了脑电与轻度抑郁症相关联的有效信息， 得到最有效的分类器为SVM方法， 最佳的特征组合为活跃度、 移动性、 小波能量熵和小波奇异熵， 最优的导联组合为O2、 T5， 以及脑电节律组合为alpha、 beta、 gamma. 在此基础上， 得到静息态抑郁脑电的识别准确率最高为94.24%、 召回率92.35%、 精确度96.23%. 该研究可以应用于轻度抑郁症的机器筛查， 为抑郁症机器识别探索了更有效的脑电处理方式.

由于本研究仅使用了静息态的抑郁脑电数据， 没有对睡眠态和诱发态的脑电数据进行机器识别和分析， 因此， 研究结果仅适用于静息态的抑郁脑电检测和分类.