不同选样方法下短历时暴雨频率分布线型优选
2022-11-28王鹏飞王双银
王鹏飞,王双银,王 晶,胡 睿
(西北农林科技大学 水利与建筑工程学院,陕西 杨凌 712100)
1 引 言
随着城市化进程加快,短历时暴雨引起城市内涝、区域性洪水等暴雨灾害发生频率增高,对人民的生命财产安全和城市可持续发展造成严重威胁[1-3]。因此,研究短历时暴雨频率分布对推求城市设计暴雨和暴雨灾害防治等方面具有重要意义。
暴雨资料选样是推求设计暴雨的基础。目前,国内外常采用年最大值法、年超大值法和年多个样法3种暴雨资料选样方法[4-6],但到底采用哪种选样方法推导出的设计暴雨精度更高,目前还没有统一定论。选取恰当的选样方法和合适的频率分布线型是研究短历时暴雨频率分布的关键[7-8],由于不同地区的降雨、水文、地理等客观因素差异较大,加之水文因素本身就存在着较大的随机性,因此每一个地区都有其所适应的频率分布线型,而目前能够较全面地考虑多种频率分布线型的优选研究还相对较少[9-12]。此外,暴雨频率分布线型的优选还需要选择恰当的拟合优度评价方法,目前国内外常用的有概率点据相关系数检验法、拟优确定性系数检验法、拟优平方和准则法和拟优绝对值准则法等[13-16]。大量科研工作者的研究表明,适宜当地情况的暴雨频率分布不仅可以揭示暴雨在时间上的变化规律,更可以为推求研究区城市设计暴雨、确定城市排水工程规模和区域性暴雨灾害防治等提供科学依据。
基于此,本文以陕西省渭河流域为研究区,采用年最大值法、年多个样法和年超大值法3种选样方法,对目前国内外常用的13种频率分布线型在短历时暴雨频率计算中的适应性进行研究,以期获得该研究区短历时暴雨频率计算的最优频率分布线型。
2 资料与方法
2.1 资料来源
研究资料是由陕西省气象中心提供的陕西省渭河流域39个气象站1981—2017年历年逐分钟暴雨资料。陕西省渭河流域各气象站空间分布见图1。

图1 陕西省渭河流域各气象站空间分布
2.2 选样方法
本文选取5、10、15、20、30、45、60、90、120、150、180 min共11个短历时统计时段,采用以下3种选样方法进行选样[4]。
2.2.1 年最大值法
该方法选取每年各历时最大降雨量组成统计样本。虽然年最大值法选样简单、独立性强,但也会遗漏降雨量大年份的部分暴雨,从而导致短重现期部分设计暴雨强度值偏小。水利工程一般设计洪水重现期较长,故普遍采用此方法。
2.2.2 年多个样法
每年选取各历时6~8个最大降雨量后统一排序,各历时选取资料年限3~4倍的最大降雨量组成统计样本。该方法兼顾多雨和少雨年份,可以有效地弥补年最大值法的缺点,但该法需要资料较多,收集困难,统计工作量大。
2.2.3 年超大值法
每年选取各历时2~3个最大降雨量后统一排序,各历时选取资料年限1倍的最大降雨量组成统计样本。该法能够保证选取到较大的降雨量,减少了统计中一些降雨量小的资料,在概率意义上与年最大值法相近,资料易得,统计工作量小。
2.3 频率分布线型
本文选取的频率分布线型包括5大类,共计13种[17],见表1。
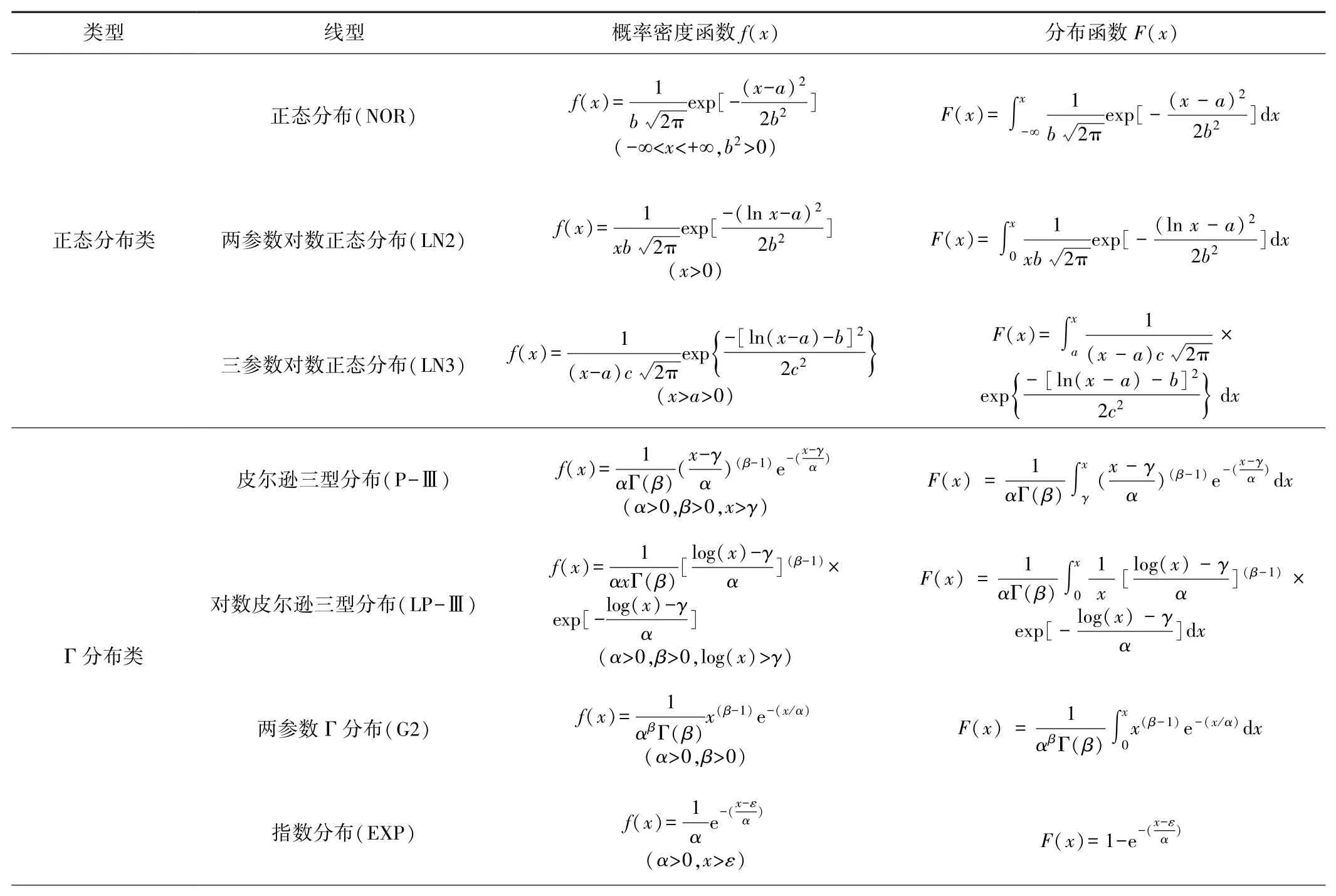
表1 频率分布线型

续表1
2.4 参数求解方法
线性矩法是概率权重矩的线性组合,其最大特点是对暴雨序列中极大值和极小值不敏感;同时,线性矩法估计量具有良好的统计特性,在小样本情况下估算参数是无偏的。因此,本文选取线性矩法作为频率分布模型的参数估计方法。
1996年Wang在Hosking对线性矩研究的基础上提出了离散样本线性矩的直接估计方法[18],计算公式如下:
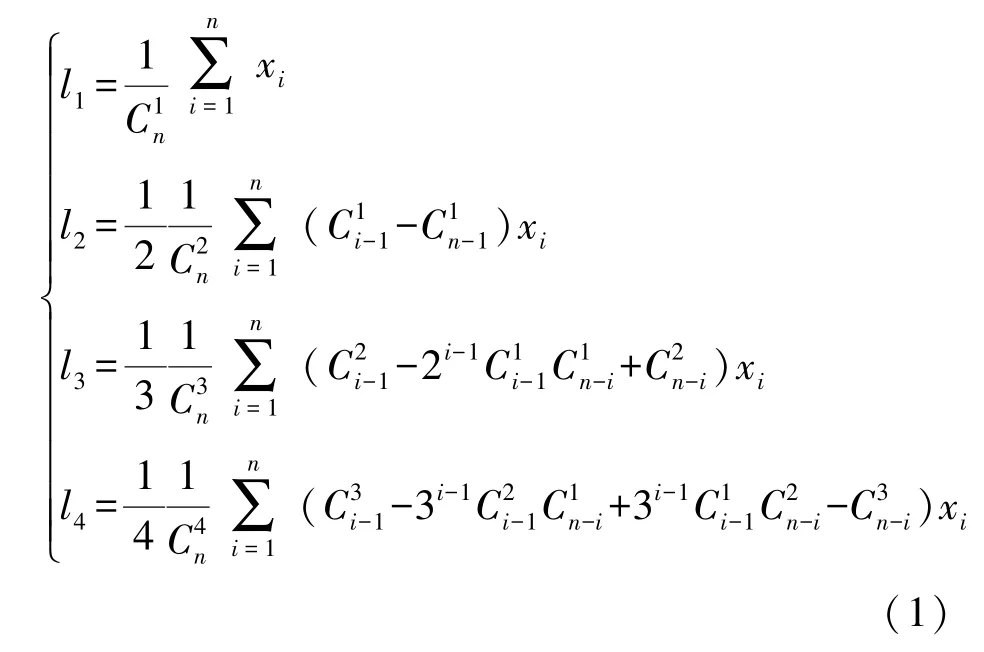
式中:xi为序列值,x1≤x2≤…≤xn;为从n个元素中取k个元素的组合数,当k>n时,=0。在线性矩已知的情况下,通过各备选分布参数与线性矩的关系可以对其进行计算[17]。
2.5 拟合优度评价方法
拟优平方和准则法[19-20]是以实测值与假设分布理论值的平均绝对均方差(RRMSE)最小原则来判定最优分布,鉴于对较大误差反应敏感的特性,选取该法作为频率分布拟合的精度评价方法。其计算方法如下:
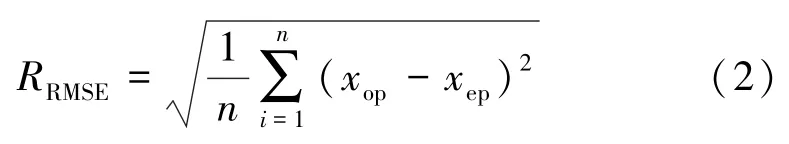
式中:xop为对应频率下实测值;xcp为假设理论分布相应频率下理论计算值。
3 结果与讨论
3.1 同一站点不同统计时段的频率分布优选
基于3种选样方法获取的暴雨资料分别适配13种频率分布模型,采用线性矩法估参,利用其估算结果分别计算各短历时暴雨序列假定频率分布计算值与实测值的RRMSE值,以此来确定各气象站和各统计时段暴雨序列最优频率分布。本文以某站为代表站,该站在年最大值法下不同统计时段各频率分布拟合优度评价结果见表2。
通过对不同频率分布线型RRMSE值的比较分析,得出凤县站年最大值法下各统计时段暴雨序列的最优频率分布情况。由表2可知,在11个历时的暴雨序列选定的最优分布中,5 min暴雨序列的最优分布为WEL,10 min暴雨序列的最优分布为GEP,15、20、30、45、60、90、120 min暴雨序列均以LP-Ⅲ为最优分布,150、180 min暴雨序列的最优分布为EXP。11个历时的暴雨序列中有7个历时的暴雨序列以LP-Ⅲ为最优分布,较其他频率分布有明显优势,且LP-Ⅲ的RRMSE均值为1.888,是13种频率分布线型中最小的,故选取LP-Ⅲ作为某站在年最大值法下短历时暴雨频率计算理论分布。

表2 某站年最大值法下不同统计时段各频率分布拟合优度评价结果
采用同样分析思路对研究区39个气象站在年最大值法、年多个样法和年超大值法3种选样方法下的最优频率分布进行探究,其结果见表3~表5。
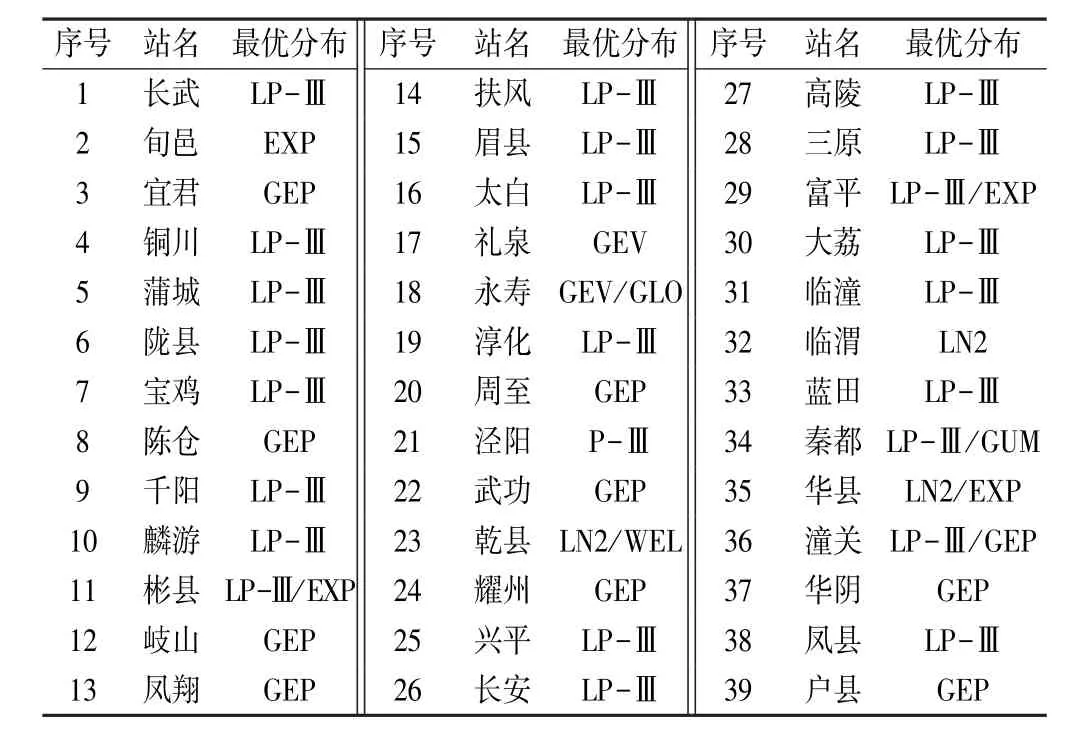
表3 年最大值法下的各气象站最优分布
由表3可知,39个气象站中,年最大值法选样时,最优分布为LP-Ⅲ分布的气象站有23个,占总数的50%;其次是GEP分布,站点数量为10个。由表4可知,年多个样法选样时,最优分布为GEP分布的气象站有28个,占总数的65%;其次是P-Ⅲ分布,其气象站数量为8个。由表5可知,年超大值法选样时,最优分布为GEP分布的气象站有25个,占总数的58%;其次是P-Ⅲ分布,其气象站数量为17个。
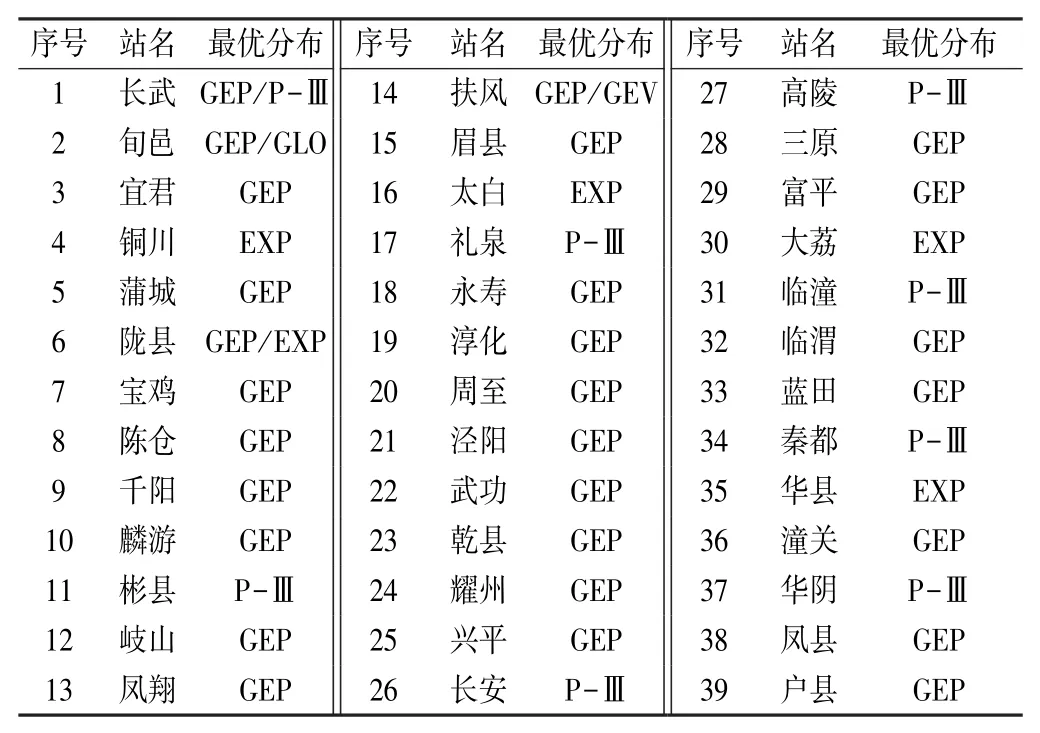
表4 年多个样法下的各气象站最优分布
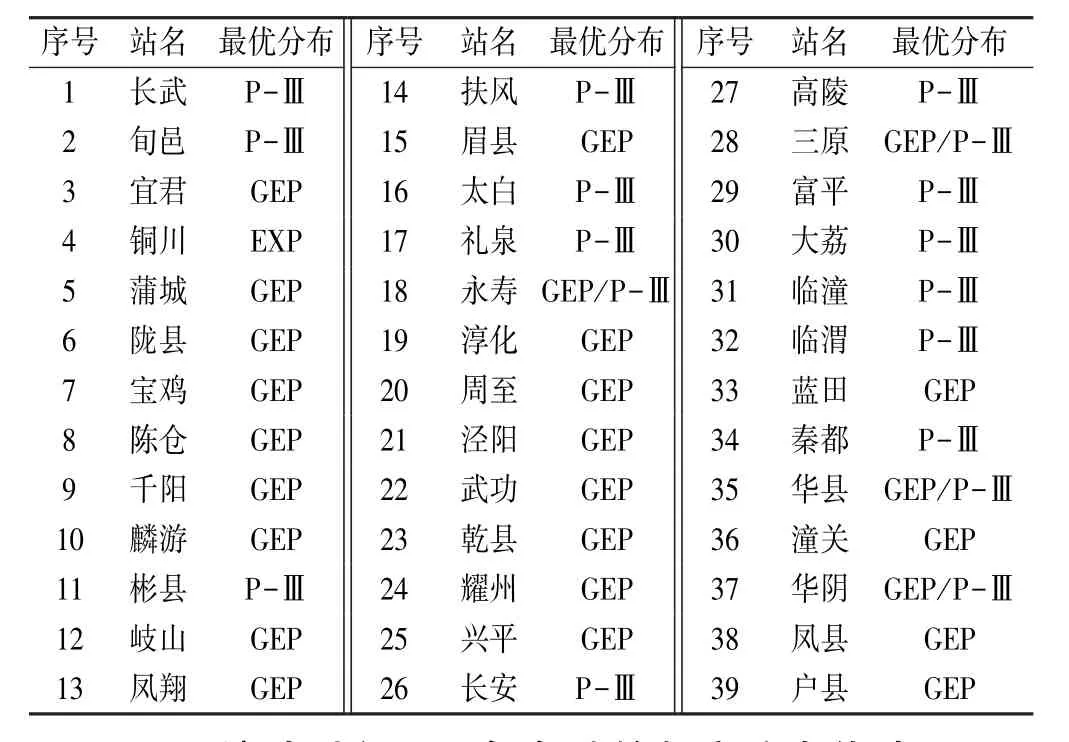
表5 年超大值法下的各气象站最优分布
3.2 同一统计时段不同气象站的频率分布优选
在不同选样方法下对11个短历时统计时段暴雨序列的不同频率分布气象站数量进行统计,绘制出不同频率分布各统计时段最优气象站数量统计图(见图2~图4)。由图2可知,LP-Ⅲ分布在图中所占比例最大,其次是GEP分布,而NOR分布、LN3分布、LGS分布适应性最差,占比为0。由图3可知,GEP分布所占比例最大,其次是P-Ⅲ分布,而NOR分布、LN3分布、G2分布和LGS分布适应性最差,占比为0。由图4可知,GEP分布所占比例最大,其次是P-Ⅲ分布,而NOR分布、LN2分布、LN3分布、G2分布和LGS分布适应性最差,占比为0。综合3种不同选样方法下拟合优度评价结果,GEP分布表现出了较强的适应性,可作为研究区各时段短历时暴雨序列最优频率分布;NOR分布、LN3分布、LGS分布适应性最差,不宜作为研究区短历时暴雨频率计算分布线型。

图2 年最大值法下不同频率分布各统计时段最优分布气象站数量统计
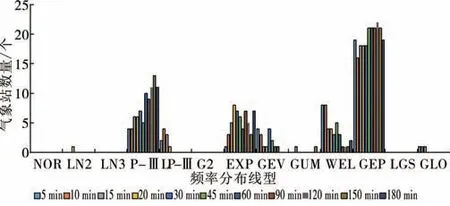
图3 年多个样法下不同频率分布各统计时段最优分布气象站数量统计
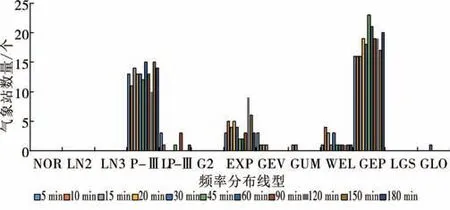
图4 年超大值法下不同频率分布各统计时段最优分布气象站数量统计
4 结 论
为探究不同选样方法下短历时暴雨频率分布线型的适应性,本文以陕西省渭河流域为研究区,选取39个气象站,采用13种频率分布线型,分别从同一气象站不同历时暴雨序列最优分布和同一历时不同气象站暴雨序列最优分布两方面进行了分析。结果表明:采用年最大值法对研究区暴雨进行选样,LP-Ⅲ分布相较于GEP分布在39个气象站和11个短历时暴雨序列中适应性占比最高,适应性更强,LP-Ⅲ分布宜作为最优分布;采用年多个样法和年超大值法对研究区进行选样,GEP分布相较于P-Ⅲ分布有明显优势,GEP分布宜作为最优分布。综合3种选样方法下RRMSE评价结果,GEP分布均表现出较好的适应性,可作为研究区短历时暴雨的理论频率分布。
