对预期赔付率假设合理性问题研究
2022-11-26刘诗佳高一宸
刘诗佳,高一宸
(1.中央财经大学 中国精算研究院,北京 100081;2.中国科学技术大学 管理学院,安徽 合肥 230026)
一、研究背景及目的
根据银保监会的监管要求,保险公司应合理评估保险责任准备金。在准备金评估过程中,一项关键工作是合理确定预期赔付率假设,该假设包括:保单年制(亦称为业务年制)下的预期赔付率假设、事故年制下的预期赔付率假设,前者用于评估未到期责任准备金,后者用于评估未决赔款准备金。
在准备金评估过程中,需要对经验赔付数据进行归集整理。该归集整理过程按照数据归集原则不同可分为两类:保单年制、事故年制,其经验赔付数据集也分别被称为保单年制下流量三角形、事故年制下流量三角形。
对同一保险业务,由于保单年制下流量三角形与事故年制下流量三角形是基于同一组业务数据按照不同数据归集原则得到的经验数据集,精算人员在此基础上分别计算保单年制和事故年制下的经验赔付率,其最终目的是:基于评估时点的存量业务和历史赔付经验,计算其保单年制和事故年制下的预期赔付率,并作为公司未来负债的评估假设,分别用于评估未到期责任准备金、未决赔款准备金。
因此,保单年制下的赔付率与事故年制下的赔付率之间应存在一定的逻辑关系。在精算实务中,受退保、批单、理赔模式调整、风险分布变化、汇率变动、理赔费用变化、追偿款收入等不确定因素影响,该逻辑关系并不直观,甚至有较强的隐蔽性。各保险公司在确定两套预期赔付率假设时,往往忽略该关系,在实务中采取一些简化方法。
为了解我国保险实务的实际情况,我们对多家保险公司的预期赔付率假设进行调研。由于预期赔付率的确定方法和结果尚未纳入保险公司信息披露范围,笔者只能通过线下方式获取相关信息。本次信息调研涉及的保险公司包括阳光财险、人保财险、长江财险、锦泰财险、广东能源财险自保、华农财险、英大财险、中银保险、中路财险、中国出口信用保险公司、国任财险、金桥海峡财险、都邦财险、黄河财险、众惠财险相互保险、长安责任保险、中原农险、阳光农业相互保险等。
调研结果显示,保险公司通常根据业务性质、行业惯例、监管要求等因素,对不同险种采用不同数据归集方法评估准备金。保险公司大多采用事故年制对保险业务按险种大类进行数据归集,计算得到事故年制下的经验赔付率,最后确定事故年制下的预期赔付率(通常等于经验赔付率)。而对于如何确定保单年制下的预期赔付率,各公司之间差异较大。据了解,目前我国财险公司通常采用以下4种转换规则:
(1)完全基于保单年制下的赔付率数据确定保单年制下的预期赔付率;
(2)保单年制下的预期赔付率=事故年制下的预期赔付率;
(3)适当上调或下降上一财务账期(即财务核算的会计期间)确定的保单年制下的预期赔付率及近期准备金回溯分析结果;
(4)根据事故年制下的预期赔付率假设,同时考虑盈余管理、偿付能力管理等因素,确定保单年制下的预期赔付率。
上述4 种方式估计保单年制下的预期赔付率存在以下问题:一是上面4种方法均未考虑保单年制与事故年制下预期赔付率之间的逻辑关系,这将最终影响保险责任准备金评估结果的科学性和合理性;二是不同公司在评估方法选择上存在较强的主观性和差异性,严重影响各保险公司财务报表的可比性;三是以管理目标人为确定赔付率有悖于监管规定。
此外,部分保险公司对特定业务采用保单年制进行数据归集,以类似的处理方法得到保单年制下的预期赔付率,最后基于一定的主观判断以保单年制下的预期赔付率确定事故年制下的预期赔付率。调研发现,该方式仍存在与前文类似的问题。
据了解,国内外学术文献中,尚未发现关于上述问题的相关研究成果。本文旨在以《关于印发保险公司非寿险业务准备金管理办法实施细则(1-7号)的通知》(银保监规〔2022〕6号)为依据,以精算理论研究为支撑,对两套预期赔付率假设之间的逻辑关系进行研究,并提出一套合理的转换规则,以及用于判断规则优劣的估计优度指标。
二、由保单年制下的预期赔付率估计事故年制下的预期赔付率
根据调研结果,部分保险公司对部分业务采用保单年制下的数据归集方式,包括养殖险、种植险、原农共体分入业务、短期出口信用险、内贸信用险等。基于保单年制数据,可估计保单年制下的预期赔付率。为合理估计事故年制下的预期赔付率,本节通过分析事故年制下与保单年制下的预期赔付之间的数学关系,给出由前者推算后者的估计公式,并判断评估质量的标准。
(一)估计公式
对某一类保险产品下的一组同质保单,假设保单的保险期限为整数T。由于保单年制和事故年制是对同一组数据采用的不同数据归集方法,根据应用场景需要,可对数据使用不同时间单位。这里以季度作为时间单位,用Ppoli表示保单季度i的承保保费(或签单保费),用LRpoli表示保单季度i的预期损失率。同时假设该类产品所有赔案具有相同发展模式,赔案在第k发展季度(占总赔付额)的赔付比例为uk,这里k=1,2,…,K。对于任意一张保单,根据所承保风险在保险期间内分布情况,假设在第k个季度所承保风险占总承保风险的比例为ωk,这里k∈(0,T+1]。在本文中,预期赔付率与预期损失率等价。
为在保单年制下的数据基础上确定事故年制下的预期赔付率假设,下面将分析二者的数学关系。
对于同一类保险产品的同一组保单业务,记事故季度j的满期保费为Paccij,预期损失率为LRaccij。令

则保单季度i的承保保费在第k发展季度的满期保费为Ppoli φk,事故季度j的满期保费为

事故季度j下第k发展季度的赔付支出为

由于保单起期到赔付发生日之间囊括了事故发生的时间,所以对于保单季度i下的第k个发展季度的现金流,需同时考虑从保单季度到事故发生季度,及从事故发生季度到目标季度k两部分。对此引入Qk:

则保单季度i下第k发展季度的赔付支出为:
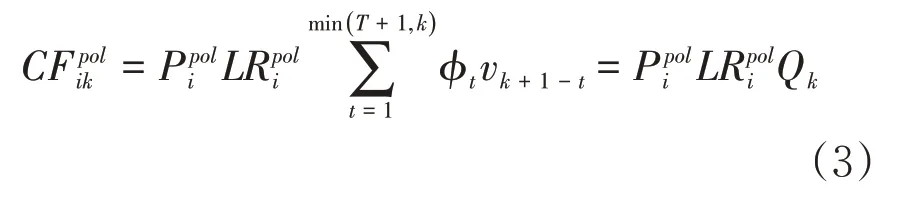
无论是在保单年制下还是在事故年制下,同一日历季度(财务季度)中发生的赔付支出之和相等。根据该原则,有:

根据(2)-(4)式可得:

这里,L为正整数,对应着日历季度L-1。

由于当i>T+1 时φi=0。此时(6)式可改写为:

这里重点考虑LRaccij与LRpoli之间的关系。在(7)式中取j=1,则可由保单年制下的数据得到事故年制下预期损失率LRacci1的公式:

取j=2,可由保单年制下的数据得到保单年制下预期损失率LRacci2的公式:

以此类推,可得到根据保单年制下的预期赔付率假设计算事故季度j的预期赔付率LRaccij的一般性公式:

(二)估计优度指标BI的设计
当j>T时,(8)式可以改写为:

令

记D0 为某评估时点,当j=L≤D0-T时,(9)式可以写作:

令

对(10)式,令L分别取D0-T,D0-T+1,…,D0,有

在精算实务中,rank()=T+1 一般成立,即矩阵满秩,其逆矩阵存在。在(11)式两侧右乘以,可获得:

记

此处BID0为事故年赔付率的估计优度,算子||.||表示对向量的每个单元的绝对值进行求和。由于UTI=1,衡量预测效果的判断标准是:BID0越接近1,则预测效果越好;反之,则越差,意味着实际情况可能与(9)式所基于的假设相背离。
(三)估计优度指标BI的应用实例
这里采用某财险公司交强险业务数据,对BI的应用进行展示。表1给出了2018Q3—2020Q4的保单季度预计赔付、借助(8)式计算得到的2019Q4—2020Q4 事故季度预计赔付,以及2019Q4—2020Q4的BID0指标计算结果。

表1 估计优度指标BI的计算
下面给出当D0=2020Q4时,BID0的计算过程。
首先,将表1中对应数据带入(12)式,可算得:

然后对(13)式计算结果应用算子||.||,可得到当D0=2020Q4时,BID0约为0.986。
表1显示,(8)式对以上5个事故季度预期赔付率的整体估计效果较好。其中,估计效果最好的是2019Q4、2020Q1,BID0非常接近1;最差的是2020Q4,此时BID0约为0.986,与1 之间的偏差较大,具体原因可能包括车险改革、疫情等。
三、由事故季度预期赔付率估计保单季度预期赔付率
在对各类保险业务进行准备金评估过程中,保险公司大多采用事故年制下的数据归集方法。本节从事故年制下的预期赔付率入手,进一步分析两套预期赔付率之间的逻辑关系,研究如何根据事故年制下的预期赔付率计算保单年制下的预期赔付率。对此,第一方案是考虑基于(7)式进行计算,但此时该方法本身存在一些问题。本节将对该方案及其存在的问题进行分析,并给出解决方案。
(一)第一方案及存在的问题
对(7)式,取j=1,可得到由事故年制下的数据计算保单年制下预期损失率LRpol1的计算公式:

在(7)式中取j=2,可得到根据事故年制下的预期赔付率{LRaccij,j∈(0,2]}计算保单年制下的预期损失率LRpol2的公式:

以此类推,根据已知的事故年制下的相关信息{LRpolj,j=1,2,…,j-1},可得到保单季度j预期赔付率LRpolj的计算公式:

在精算实务中,用(14)式计算保单季度i的预期赔付率LRpoli时,往往要面临以下问题:
(1)在计算过程中,需用到以前各保单季度相关信息,对于长期开展的业务,该部分数据量大,计算效率低;
(2)对于部分历史保单季度预期赔付率等信息缺失的情形,无法用(14)式得到保单季度预期赔付率;
(3)受退保、监管要求、IT系统等因素影响,保单年制下的签单保费数据与事故年制下的满期保费数据并不完全吻合,此时据(14)式计算得到的结果可能不合理,甚至无法使用;
(4)公式所用假设,在实务中并不严格满足,如保单季度内保单生效日分布的均匀性假设、所承保风险分布的均匀性假设和各事故季度赔付模式的一致性假设等;
(5)保单季度i的预期损失率LRpoli影响着事故季度i,i+1,…,i+T,仅根据事故季度i及以前季度来估计保单季度i的预期损失率LRpoli,丢失信息过多,估计结果可能有较大偏差;
(6)对于距评估时点最近的日历季度,其对应的事故季度的经验数据中所含的最近保单季度的赔付信息较少,以(14)式估计最近保单季度的预期赔付率较困难。
基于上述问题,下面我们尝试寻找一个更加可行的解决方案。
(二)第二方案的提出
回顾(8)式,根据保单年制下各季度预期赔付率LRpoli、承保保费Ppoli,以及事故年制下满期保费Paccij,可计算事故年制下各季度预期赔付率LRaccij,公式为:

前文提过使用(14)式丢失信息太多,这将使估计结果存在问题。对此,提出另外一种思路。
保单季度i对第j事故季度(i≤j≤T+i)的满期保费的贡献为Ppoli φj-i+1,对已发生赔付支出的贡献为Ppoli φj-i+1LRaccij。对j∈[i,T+i]求和,保单年i的总赔付支出为

从而得到保单季度i的预期赔付率

(16)式是以事故年制下季度i及后续T个季度的预期赔付率计算保单年制下季度i的预期赔付率。若记当前评估季度为Da,则可采用类似的方法根据事故年制下季度Da及以前季度的预期赔付率,计算得到保单年制下保单季度i的预期赔付率{LRpoli,i≤Da}:

(17)式也可简写为:

(14)式和(18)式两种方法的主要差异在于假设不同。(14)式的假设是:各保单季度具有相关的预期赔付率,此时,各事故季度下来自不同保单季度的满期业务具有不同的预期赔付率,优点是重复利用以前保单季度信息。(14)式是在过去事故季度预期赔付率基础上,估计各保单季度的预期赔付率,若这部分历史数据不可获得或者可信度较低,则该公式不适用。(18)式的假设是:各事故季度具有相同的预期赔付率,而对特定保单季度,其赔案发生在不同的事故季度,从而具有不同的预期赔付率。(18)式将这些预期赔付率按照所承保业务在各事故季度的风险比例分配情况加权平均,得到各保单季度的预期赔付率,优点是重复利用各保单季度所承保业务在后续赔付发展季度中的赔付率信息,当基础数据中保单年制下和事故年制下的数据不完全吻合时,计算结果更稳定且更有可操作性。
(三)第二方案下满期保单季度估计优度指标FI的设计
对满期保单季度,截至评估时点,其所需的(事故季度下)赔付信息是完整的,无需对未来赔付进行预测。针对本文的估计模型,同样给出一个估计优度指标。
令

记D0 为某评估时点。(17)式中当L≤D0-T时,LRpoli可以写成

记


在精算实务中,rank()=T+1 一般成立,即该矩阵可逆。在(21)中两边右乘以,则有

由于UTI=1,记

此处FID0-T为估计优度,算子||.||表示对向量的每个单元的绝对值进行求和。由于UTI=1,FID0-T衡量预测效果的判断标准是:FID0-T越接近1,则预测效果越好;与1 之间的偏差越大,则预测效果越差,此时往往意味着(18)式所采用的假设发生了变化。
(四)估计优度指标FI的应用实例
这里采用某财险公司交强险业务数据,对FI的应用进行展示。表2给出了2019Q3—2021Q4的事故年制预期赔付率,借助(18)式计算得到的2019Q4—2020Q4 的保单年制预期赔付率,以及2019Q4—2020Q4的FIL-T指标的计算结果。

表2 估计优度FI的计算
下面给出当D0=2021Q4 时,FID0-T的计算过程。首先,将表2中对应数据带入(21)式,可得:

然后对(22)式计算结果应用算子||.||,可得到当D0=2021Q4时,FID0-T约为1.130。
根据表2,各季度的FID0-T均大于1,其中,当D0=2021Q1时,FID0-T最接近于1,附加波动,即预测效果尚可;当D0=2020Q4及D0=2021Q2时,预测效果较差,FID0-T分别约为3.838和2.593。
在此示例中,在事故季度的预期赔付率假设符合实际的前提下,FID0-T偏高的可能原因有以下两种:第一,FID0-T所基于的假设与现实情况不符,这里的假设指任意保单的风险分布比例{φk,k∈[1,T+1]}与保单季度i、事故季度j 及对应的日历季度无关;第二,此处所采用的赔付率评估模型假设与现实情况不符,这里的假设指预期赔付率只受保单季度、事故季度的影响,若预期赔付率受日历季度(财务季度)影响较大,如受特定时期突发疫情影响,导致该时期事故季度的预期赔付率出现大的波动,则本文模型可能失效。
此示例所考虑的财险业务为交强险,在新冠肺炎疫情的特殊背景下,车辆使用次数、运行里程、报案次数等都有所下降,最终使得下降,导致D0=2021Q1时FID0-T的精算模型失效。
(五)第二方案下未满期保单季度预期赔付率的估计
对于未满期的保单季度,截止到评估时点,其赔付信息尚不完整。只能依赖事故年制下的部分信息去估计未满期保单季度的预期赔付率。
若采用(18)式计算保单季度i的预期赔付率{LRpoli,i≤Da},则当i∈[Da-T+1,Da]时,由于截至评估时点,保单年的满期保费比例不足100%,不完全的信息基础可能会导致较大误差。特别是当i=Da时,对LRpoli的估计只用到了,而中关于的部分只占φ1,其余部分与{LRpoli,i∈[Da-T,Da-1]}密切相关。为提高估计结果准确性,借助(8)式对(17)式进行修正:
第一步,根据事故季度{LRaccij,j≤Da}计算保单季度的{LRpoli,i≤Da},记为{#1LRpoli,i≤Da},这里左上标#1 代表第1 轮计算;同时,把各事故季度预期赔付率{LRaccij,j≤Da}记为#1LRaccij:

#1LRaccij=LRaccij,j≤Da
第二步,根据各保单季度的预期赔付率{#1LRpoli,i≤Da},计算各事故季度的预期赔付率{#2LRpoli,j≤Da}:

第三步,根据各事故季度的预期赔付率{#2LRpoli,j≤Da},计算各保单季度的预期赔付率{#2LRpoli,i≤Da}:

类似地,后续可进行更多轮的计算,得到各轮的预期赔付率估计值。若经验数据质量较好且事故年制下及保单年制下基础数据具有较强的一致性,则该计算过程中第二步的分母为正,通常情况下各保单年制下的预期赔付率是收敛的;若基础数据有问题,导致计算结果不收敛,此时运行2~3轮即可。
由于未满期保单的赔付数据尚不完整,对其预期赔付率估计值的好坏需等到满期后才可用前文估计优度指标回溯分析。
(六)未满期保单季度预期赔付率估计的实例分析
下面,使用某财险公司交强险业务相关数据,计算保单季度的预期赔付率,如表3所示。

表3 预期赔付率LRpi ol计算 评估时间:2021-12-31
在表3中,已知项目包括对应保单季度的签单保费Ppoli、对应事故季度的满期保费Paccii及预期赔付率LRaccii。其中,各事故季度的满期保费Paccii是由精算人员依赖流量三角形、准备金回溯分析、理赔模式变化、经济环境变化、业务风险特征等信息进行确定的。
表3中所考虑的保险期限是4 个季度,故2020Q3、2020Q4 的业务已经满期,在各轮迭代计算中无需调整,需调整的是未满期的2021Q1-2021Q4预期赔付率估计值。表3给出了采用前文方法得到的、未满期保单季度所对应的预期赔付率LRpoli在各轮的估计值#1LRpoli、#2LRpoli、#3LRpoli。由表3发现,各轮得到的计算结果波动较大,本身也反映出实际数据的复杂性。这里迭代计算三次后结束,实际工作中精算人员需要根据情况合理确定迭代次数。
四、结论与建议
为提高某一类财险非寿险业务预期赔付率假设的合理性,保险公司可按照保单季度、事故季度对赔付信息进行分类归集,综合内外部信息和发展趋势,确定各保单季度、事故季度的预期赔付率。据调研,保险公司对大多数非寿险业务通常选择记录事故年制下的完整数据,因此,可借助精算方法得到事故年制下的预期赔付率;而保单年制下的基础数值不够完整,不足以直接评估保单年制下的预期赔付率假设。目前保险公司常用的几种预期赔付率假设确定方法存在一些缺陷,可能会影响后续精算评估的科学性、合理性、可比性和合规性。由于确定预期赔付率假设是精算实务中一项重要工作,本文通过分析二者数理关系,提出根据事故年制下的预期赔付率计算保单年制下的预期赔付率的合理方法。
此外,本文所提出的评估方法具有较强的实操性。前文模型中使用分析数据及部分假设,如vj、φk、LRaccij分别对应《关于实施保险公司偿付能力监管规则(Ⅱ)有关事项的通知》(银保监发〔2021〕52号)附件11-1——《财产保险公司偿付能力压力测试报告Excel 样表》中的各险种赔款发展年度中各年赔付比例、保费收入赚取比例假设和赔付率假设。另外,虽然文件的样表以年度为单位,但很多保险公司采用季度或月度作为最小单位进行预测,更小的颗粒度可以提高估计的科学性。
为规范保单年制下和事故年制下的预期赔付率假设,建议中国精算师协会加强对相关问题的研究,以行业自律形式发布相关规范性文件,明确保险公司在确定预期赔付率假设时应遵循的原则,厘清保单年制下和事故年制下的预期赔付率假设的关系,提升行业准备金评估工作的技术水平和公司内部管理水平。本文的结论可广泛应用于准备金评估、保费充足性测试、压力测试、回溯分析、产品开发、再保险安排、资产负债管理等公司内部管理活动。
