基于二维朗奇相位光栅的四波横向剪切干涉定量相位成像

宋金伟，闵俊伟，袁勋，薛雨阁，姚保利

（1 中国科学院西安光学精密机械研究所瞬态光学与光子技术国家重点实验室，西安 710119）（2 中国科学院大学，北京 100049）

0 引言

定量相位成像（Quantitative Phase Imaging，QPI）具有无标记、非入侵和三维观测等特点，已经在工业检测［1］、生物医学［2］和材料科学［3］等诸多领域中获得了广泛的应用。根据相位成像的不同原理，定量相位成像可分为干涉测量法和强度分析法两大类。前者是基于光波干涉的原理，将样品的相位分布转换为干涉条纹强度分布，然后通过对干涉图的解调来实现对样品相位的定量测量，常见的有数字全息［4］和衍射相位成像［5-6］等。这类方法测量精度高，但其中的干涉结构调节要求高且容易受到外界环境的干扰。强度分析法不需要复杂的干涉结构和苛刻的实验环境，从采集到的光波轴向系列衍射强度图像中，经过特定的算法来恢复相位分布，如GS（Gerchberg-Saxton）迭代算法［7］、混合输入输出迭代算法［8］、强度传输方程［9］方法等。但迭代方法需要反复的迭代步骤，基于强度传输方程的方法需要在不同位置记录多幅图像，这都使得成像速度慢，难以用于实时观测。

相比于上述几种方法，基于四波横向剪切干涉（Quadriwave Lateral Shearing Interferometry，QLSI）的定量相位成像具有无需参考光、结构简单、稳定性高、成像速度快等优势。HASEGAWA M等［10-11］利用二维振幅光栅和级次滤波窗口组合构建了一套四波剪切干涉成像装置，实现了对光刻系统中波前的快速检测。但这种方案需要级次滤波窗口的精确对准，调节要求高，装置复杂。PRIMOT J等［12-13］利用改进型哈特曼掩膜板提出了一种结构紧凑的四波剪切干涉方法，并将其应用于显微成像领域，实现了对生物样品的定量相位测量。但制作改进型哈特曼掩膜板需要将传统哈特曼掩膜板和棋盘相位板进行精准匹配，且对入射光的能量利用率较低。LING T等［14］提出了一种基于随机编码混合光栅的四波剪切干涉方法，使衍射光能量更加集中在四束一级衍射光上，但随机编码混合光栅结构复杂，设计和加工难度高，不易普及使用。此外，在现有文献中，尚未有人对分光元件周期、探测器像元尺寸、照明波长等因素对四波剪切干涉定量显微成像的影响进行定量分析。

本文利用二维朗奇（Ronchi）相位光栅作为分光元件，将包含样品信息的物光一分为四，通过四束衍射光之间的横向剪切干涉，实现对样品的定量相位成像和测量。由于采用纯相位光栅，对入射光能量利用率高。通过理论分析光栅周期对剪切干涉成像的影响，确定了光栅周期和探测器像元尺寸的最佳匹配关系，可以更好地利用探测器的空间带宽积，实现高分辨成像。通过分析照明波长对相位重建结果的影响，论证了宽光谱光源照明下定量相位成像的可行性。在理论分析的基础上，设计构建了基于二维朗奇相位光栅的四波剪切干涉定量相位显微成像装置，实现了对PMMA微球、微透镜阵列和葡根霉菌的三维形貌测量和定量相位成像。

1 理论分析

二维朗奇相位光栅的结构如图1所示。每4个边长为p的单元构成一个光栅周期单元，即光栅周期d=2p，相邻单元之间的相位延迟为π。

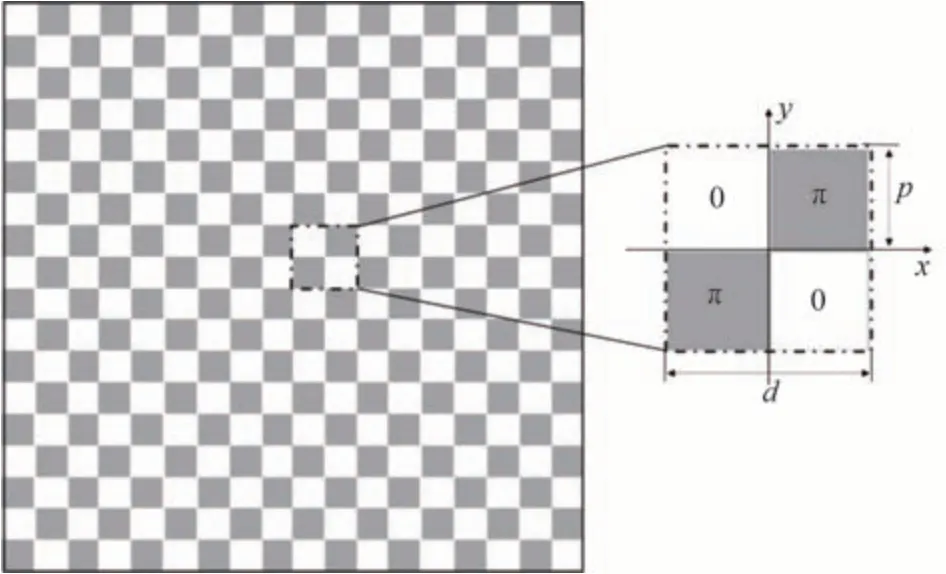
图1 二维朗奇相位光栅结构示意图Fig.1 Schematic showing the structure of 2-D Ronchi phase grating

该二维朗奇相位光栅的复振幅透过率可以表示为［15］

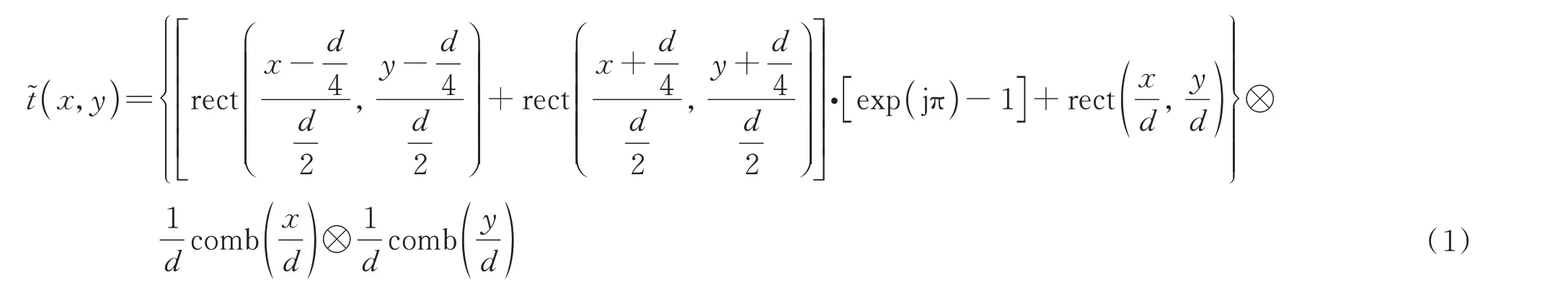
式中，（x，y）表示空间坐标，rect(·)为矩形函数，comb(·)为梳状分布函数，⊗表示卷积运算。根据光波标量衍射理论，光场的夫琅禾费远场衍射为光场的傅里叶变换。当入射光为单位振幅平面波时，对式（1）进行傅里叶变换并取模平方运算，可得光栅后的第（n，m）级衍射光的衍射效率ηn，m为

式中，F表示傅里叶变换。根据式（2）计算出四个一级衍射光的衍射效率均为16.43%，四束一级衍射光的能量之和占入射光能量的65.72%，远高于改进型哈特曼掩膜板的37%。图2给出了透过二维朗奇光栅后各级次的衍射效率分布。从图中可以看出，零级光（0，0）、级次n或m为偶数的衍射光被完全消除，衍射光的能量主要集中在四束一级衍射光上，其它级次衍射光的衍射效率远远小于四束一级衍射光，其影响基本可以忽略。

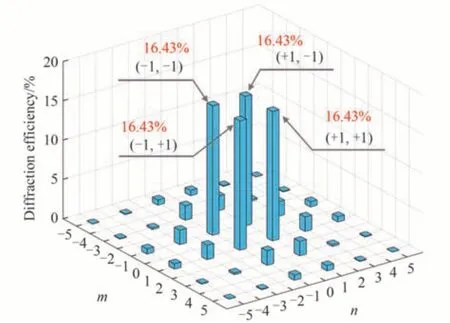
图2 二维朗奇相位光栅各级次衍射效率分布Fig.2 The diffraction-order efficiency distribution of 2-D Ronchi grating

当包含样品信息的物光，如图3（a）所示，照射到二维朗奇相位光栅后，其四束一级衍射光将沿着各自的衍射方向进行传播，如图3（b）所示。经过z距离的传播后，四束一级衍射光彼此之间将发生干涉，形成如图3（c）所示的四波横向剪切干涉图。干涉图的强度分布可以推导出为

式中，I0为二维朗奇光栅后z=0位置处干涉图强度的最大值，OPD（x，y）为样品引入的光程差（Optical Path Difference，OPD），和分别表示OPD在x方向和y方向的梯度。对式（3）进行傅里叶变换可得

式中，δ为狄拉克函数。由式（4）可知，四波横向剪切干涉图的频谱中包含有9个成分，如图3（d）所示。其中零级频谱（0，0）对应入射波前的强度信息。选用合适的滤波器滤出x方向和y方向的一级频谱，并对其进行傅里叶逆变换，可以得到如图3（e）和3（f）所示的OPD在两个正交方向上的梯度分布

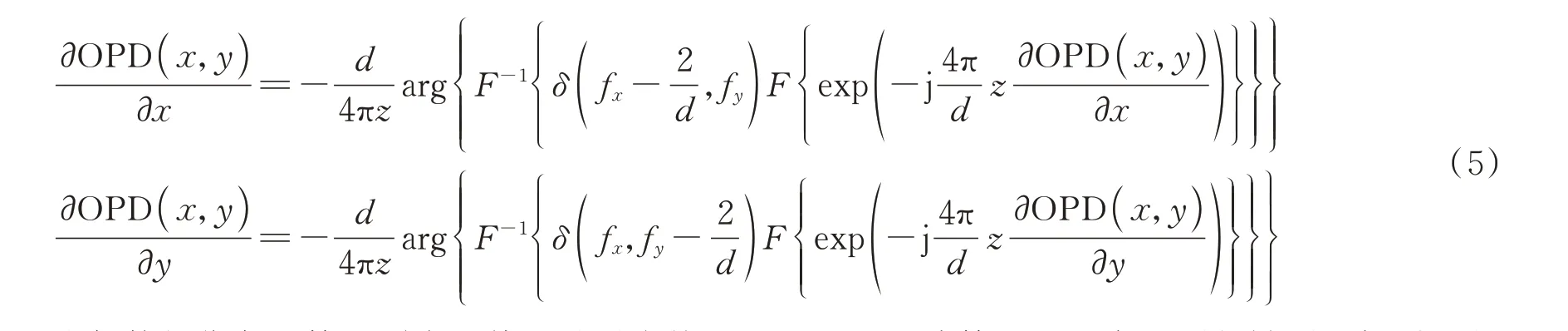
式中，arg表示取复数相位角运算，F-1表示傅里叶逆变换。最后通过积分算法即可定量测得被测目标引入的OPD分布，如图3（g）所示。重建方程［16］为

当入射波长λ确定时，可从再现的OPD分布中计算得到样品的相位分布

该方法的理论分析过程如图3所示。

从式（4）和图3（d）可知，干涉图一级频谱中心与零级频谱中心之间的距离为2/d。在进行频谱滤波时，滤波窗口的半径R通常选为一级频谱到零级频谱之间距离的一半［16］，即R=1/d。因此，为了获得最佳的再现效果，光栅周期d的选择十分重要。以一维情况为例，假设探测器像素的水平尺寸为x，水平方向的像素数为M，则探测器靶面的横向尺寸为L=M·x，频域空间的最小间隔为1/L。设光栅周期d为探测器像素尺寸的k倍，则一级频谱中心到零级频谱中心之间距离在频域空间所对应的像素数N为

则一级频谱中心与零级频谱中心之间的距离在频谱水平方向上所占的比例β为

β的大小决定了频谱滤波的半径。当β较小时（β=1/4），如图4（a）所示，干涉图各级频谱向零级频谱靠拢，使得有效滤波范围过小，频谱滤波时易受到周围频谱的干扰，且大部分高频信息将丢失，导致再现像的分辨率较低。当β太大时（β=1/2），如图4（b）所示，各级频谱虽然可以充分分开，但所需的一级频谱位于频域的最边缘，有一半的频谱信息将丢失。当β=1/3时，如图4（c）所示，一级频谱中心与图像边缘之间的距离恰好为一级与零级频谱之间距离的一半，能够最大限度地利用相机空间带宽积，保证频谱信息的完整，使得重建图像具有高空间分辨率。因此光栅周期d的最佳尺寸应为探测器像素尺寸的6倍。

图4 光栅周期为探测器像素尺寸的不同倍数时的干涉图频谱Fig.4 The spectrum of interferogram when the grating period is different times of the pixel size

此外，朗奇相位光栅相邻单元之间的相位延迟只在设计波长照明时才为π。在实际应用中，入射波长λ与理想设计波长存在差异，使得光栅相邻单元中的实际相位延迟不为π，导致光栅的各级衍射效率发生变化，影响四波剪切干涉成像效果和测量精度。

以照明光λ=550 nm为设计波长所对应的理想一维朗奇相位光栅为例，分析不同照明波长对四波剪切干涉定量相位成像的影响。图5显示了入射波长λ分别为550 nm，500 nm，458 nm和423 nm时光栅各级衍射光的归一化强度分布。此时，朗奇相位光栅中相邻单元之间的相位延迟分别为π、1.1π、1.2π和1.3π。从图5中可以看出，当光栅相邻单元之间的相位延迟非π时，透过光栅后偶数级次的衍射光仍会被抑制，但零级衍射光将出现。入射光波的波长偏离设计波长越远，零级衍射光的能量越高。当传播z距离后，零级光也将与一级衍射光发生干涉，反映到频域空间就是产生如图6（b）中点圆所示的干扰频谱项。但幸运的是，因为频谱滤波半径R是一级频谱到零级频谱之间距离的一半，所以零级和一级衍射光之间干涉所产生的频谱恰好在这个滤波范围之外，因此在一定照明波长范围内，频谱滤波并不会提取到干扰频谱的信息。

图5 不同入射波长时一维朗奇相位光栅各衍射级次的归一化强度分布Fig.5 The normalized intensity distributions of each diffraction order of 1-D Ronchi phase grating at different incident wavelengths

图6 不同相位延迟时的干涉图频谱Fig.6 The spectrum of interferogram at different phase delay

为了定量地分析不同照明波长对所提方法的影响，以peaks函数作为输入，分析了照明波长从390 nm到920 nm时基于四波剪切干涉的定量相位成像测量误差（二维朗奇相位光栅设计波长550 nm），结果如表1所示。以相对误差率不超过5%作为评判标准，可以发现照明波长在407～846 nm之间时，所提方法都可以得到准确的结果。该结论表明，基于二维朗奇相位光栅的四波剪切干涉对照明光的波长不敏感，因此可以使用宽光谱光作为照明光源，这也为该技术与普通光学显微镜的结合奠定了基础。

表1 照明波长从390 nm到920 nm时重建peaks函数相位图的相对误差率Table 1 The relative error rates of reconstructed phase maps of peaks function at different illumination wavelengths from 390 nm to 920 nm

光栅相邻单元之间的相位延迟φc除了受到照明波长的影响之外，还会受到刻蚀深度h的影响

式中，nc为光栅材料的折射率。当入射波长为设计中心波长、深度h出现刻蚀误差时，相邻单元之间的相位

延迟也会偏离π。根据前面的分析，相位延迟在0.65π到1.35π之间可以得到准确的恢复结果，因此刻蚀深度的容错率为35%。

2 定量相位显微成像实验

为了验证所提方法的可行性和有效性，搭建了如图7所示的实验装置。其中，图7（a）为装置原理示意图，图7（b）为装置实物图。将研制的四波横向剪切干涉模块直接接在商用倒置光学显微镜（BX22PHD228S，奥斯微，中国）。激光器（MGL-FN-532-100 mW，长春新产业公司，中国）输出的532 nm照明光经透镜L1（f=125 mm）准直和反射镜M1反射后照射到样品上。包含样品信息的物光经显微物镜（40×，NA0.60）收集后，经显微成像系统照射到二维朗奇相位光栅上发生衍射。该光栅的周期d=54 μm，对532 nm光束的相位延迟为π。经过光栅衍射后形成的四波剪切干涉图被位于光栅后z=1.7 mm处的CCD相机（BFS-U3-16S7M，FLIR Systems Inc.，美国）所接收。该相机的像素尺寸为9 μm×9 μm，像素数为1600×1100。光栅周期是像素尺寸的6倍，满足最佳成像要求。

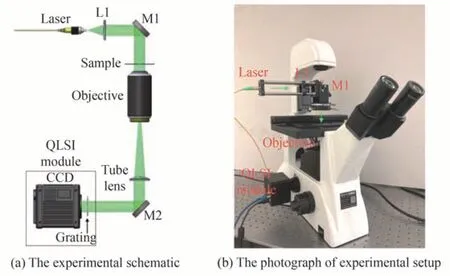
图7 实验装置原理图及实物图Fig.7 Schematic and photograph of the experimental setup

为了验证该装置相位测量的准确性，首先对直径为86 μm的聚甲基丙烯酸甲酯（Polymethyl Pethacrylate，PMMA）微球进行观测。PMMA微球被浸润在甘油中。在532 nm波长下，PMMA微球和甘油的折射率分别为1.4937和1.4748，因此微球引入的OPD最大值为1625 nm。实验记录的四波横向剪切干涉图如图8（a）所示。通过频谱滤波和相位重建后，再现的微球OPD分布如图8（b）所示。为了检验观测结果的准确性，沿再现的PMMA微球OPD分布中心划一剖面线，其对应的OPD分布如图8（c）所示。测得OPD的最大值为1595 nm，与理论值相对误差为1.8%，表明所提方法具有较高的测量精度。

图8 PMMA微球的实验结果Fig.8 The experimental results of PMMA bead

为了进一步验证所提方法在宽光谱光源照明下的观测效果，将实验装置中的光源换为普通显微镜中使用的卤素灯，选用微透镜阵列（MLAS10-F05-P150-AB，LBTEK Inc.，中国）作为被测样品。该微透镜阵列由熔融石英制成，每个透镜的直径为150 μm，微透镜的最大厚度为1.1 μm。图9（a）和（b）分别为样品在532 nm激光束和卤素灯照明下测得的OPD分布。图9（c）为（a）和（b）中红色虚线处所对应的高度曲线，其中黑色曲线为卤素灯照明下测得的OPD，红色曲线为532 nm激光照明下测得的OPD。从图中可以看出，二者测得的结果基本一致，证明了基于朗奇相位光栅的四波剪切干涉装置对照明波长不敏感，在宽光谱光源照明下也能获得良好的成像结果。由于卤素灯光源相干噪声小，其测得的OPD分布显得更为平滑，信噪比更高一些。但在进行相位换算时，波长的选择会影响测量精度。该特性表明，当测量精度允许时，可以通过在普通的光学显微镜的相机前加入合适的二维朗奇相位光栅，无需其它辅助元件或特殊结构设计即可实现对目标的定量相位测量。

图9 微透镜阵列在不同光源照明下的重建结果Fig.9 The reconstructed results of microlens array at different illuminations of light sources

进一步，使用显微镜自身的卤素灯作为照明光源，对葡根霉菌切片进行了观测。相机记录的四波剪切干涉图和再现的样品OPD形貌分布分别如图10（a）和10（b）所示。从图10（b）中可以清晰分辨样品不同位置的特征，表明所提方法可以和普通光学显微镜相结合以实现对微观样品的定量相位显微成像，有助于定量相位成像技术的进一步推广普及。

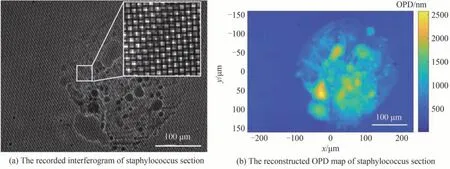
图10 葡根霉菌切片的实验结果Fig.10 The experimental results of staphylococcus section

3 结论

本文提出的利用二维朗奇相位光栅作为分光元件实现四波剪切干涉定量相位成像的方法，具有结构紧凑、稳定性高、成像速度快的特点。理论分析了光栅周期、探测器像素尺寸、照明波长、光栅刻蚀深度等因素对四波横向剪切干涉定量相位成像的影响。当光栅周期为探测器像素尺寸6倍时，可以使探测器的空间带宽积利用率到达最佳，同时该方法具有对照明波长不敏感的特性。设计构建了一套结构简单、紧凑的四波横向剪切干涉定量相位显微成像装置，以PMMA微球、微透镜阵列和葡根霉菌作为被测样品，实现了定量相位成像和测量。实验结果验证了该方法对照明波长不敏感，可用于宽光谱光源照明，可以方便地和普通光学显微镜相结合，具有更好的普适性。除了文中分析的因素外，光栅与探测器靶面之间的距离、剪切量的大小、其它高级次衍射光之间的干涉等因素也会影响本方法的相位观测精度，将在后续的工作中继续开展相关研究。