基于小波包分解和SVM的φ-OTDR系统信号识别

卜泽华，毛邦宁，司召鹏，龚华平，徐贲，康娟，李裔，赵春柳

（中国计量大学 光学与电子科技学院，杭州 310018）

0 引言

随着物联网时代的高速发展，对外界各种信息的感知和获取日益重要。与传统方法相比，相位敏感光时域反射计（phase-Sensitive Optical Time Domain Reflectometry，φ-OTDR）以较低的成本实现了大规模、长距离的测量［1］，具有灵敏度高［2-3］、分辨率高［4］、并且结构简单［5］的优点，能够同时对扰动信号进行多点检测［6］。φ-OTDR在空间域定位扰动的位置，在时间域获取扰动的振动信息。目前，φ-OTDR正在许多应用中发挥着重要作用，例如结构裂缝检测［7］、铁路监测［8］、交通流检测［9］、车辆检测等［10］。

随着实际应用场景的多样化和复杂化，对外界不同模式的信号识别成为近些年研究的重点。模式识别可以自动将检测到的振动信号根据其信号特征分为感兴趣的扰动信号和不需要的环境噪声信号，从而显着提高报警精度，降低系统的误报率。2016年，VILLAMIZAR DELGADO S等［11］通过经验模态分解（Empirical Mode Decomposition，EMD）减小光谱信号频率信息的特征离散度并采用神经网络对振动信号进行分类；神经网络训练时间长，且随着振动信号种类的提升，处理效果局限性较大。2017年，AKTAS M等［12］通过直接探测型φ-OTDR系统，采用五层神经网络并结合短时傅里叶变换（Short-time Fourier transform，STFT）系数实现对镐挖、铲挖、强风、发电机噪音等六种典型观察到的事件实现93%以上的威胁分类准确度；但STFT在对信号进行分析时，时间分辨率和频率分辨率为互斥的关系，两者无法兼顾。2018年，XU Chengjin等［13］提出一种基于时频分析和卷积神经网络（Convolutional Neural Network，CNN）的方法，该方法对挖掘、行走、车辆通过和破坏四种不同振动事件的信号样本处理后，振动事件的识别率达到90%，但CNN处理图像时间较长。2019年，WU Jun等［14］通过多尺度一维CNN提取信号的时域和频域特征，并利用全连接层和Softmax层进行识别，识别准确率达到96.59%并减少了计算时间，但该方法需要大量样本；同年，WANG Zhaoyong［15］等采用深度双路径网络（Deep Dual-Path Network，Deep DPN）对干扰事件进行分类，准确率达到97%，然而更深的网络结构带来了更长的训练时间，增加了训练负担，导致对信号进行分类所需的计算时间是采集时间的数倍。2020年，ABUFANA S A等［16］采用变分模态分解（Variational Mode Decomposition，VMD）技术从扰动信号中提取高阶统计量（Higher Order Statistical，HOS），包括偏度、峰度和方差作为样本特征，并在不同信噪比下采用线性支持向量机（Linear Support Vector Machine，LSVM）进行扰动信号识别。当信噪比从-8 dB～-18 dB提高到-4 dB～-8 dB时，识别准确率从75.2%上升到79.5%，识别的综合准确率较低。2021年，SHA Zhou等［17］提出将分布式光纤传感器和YOLO（You Only Look Once）算法相结合的方法，可以在网络中同时确定边界框和对事件进行分类；然而，该方法只能检测到单一类型的事件。

小波包变换具有良好的时频局部化特性，能有效处理非平稳信号；支持向量机（Support Vector Machine，SVM）是从统计学习理论中衍生出的一种学习方法，与传统的机器学习相比性能更好。将小波包变换与SVM结合的目标检测方法已经在许多领域广泛应用，如气阀故障诊断［18］，局部放电识别［19］等。

本文在基于相干探测型φ-OTDR系统的基础上，提出一种将小波包分解和SVM结合的信号识别方法。对实际应用中的敲击（模拟应力破坏）、晃动（模拟攀爬）、人员行走以及环境噪声四种不同事件的信号进行分析，通过小波包分解得到信号的能量特征向量作为输入样本并结合SVM进行不同事件的信号识别，提高了φ-OTDR系统信号识别的准确性。

1 基于相干探测的φ-OTDR系统

如图1所示，窄线宽光源（Narrow Linewidth Laser，NLL）线宽为3 kHz，输出功率为25 mW；光源发出的连续光经过90∶10的耦合器被分成两路，其中一路90%的信号光经过声光调制器（Acousto-Optic Modulator，AOM）调制为脉冲光并产生一个移频量，移频量大小为AOM的中心频率80 MHz，脉冲宽度为100 ns。脉冲光经过掺铒光纤放大器（Erbium-Doped Fiber Amplifier，EDFA）进一步放大功率，补偿插入损耗和传输损耗。放大后的脉冲光经过环形器的1端口并从2端口入射到传感光纤中，返回的后向瑞利散射光经过环形器的3端口与另外一路10%的本振光通过3 dB耦合器发生干涉并产生拍频信号。拍频信号由平衡探测器（Photoelectric Balance Detector，BPD）接收并完成光信号到电信号的转换；BPD最大频率响应100 MHz。最后，数据采集卡（Data Acquisition Card，DAQ）以200 MSa/s的采样频率记录数据。

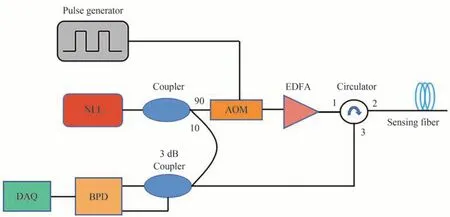
图1 基于相干探测的φ-OTDR系统Fig.1 φ-OTDR system based on coherent detection

返回的后向瑞利散射光表示为

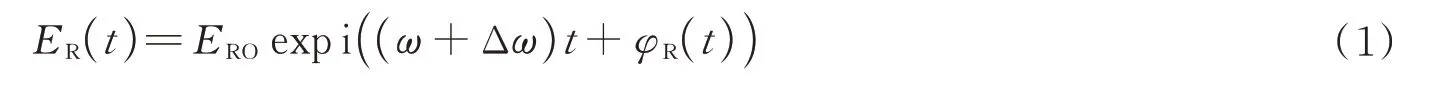
式中，ERO是后向瑞利散射光的幅度；ω是窄线宽光源角频率；Δω是AOM的移频量；φR(t)是散射光的相位。本振光表示为

式中，ELO是本振光的幅度；φL(t)是本振光的相位。拍频信号表示为

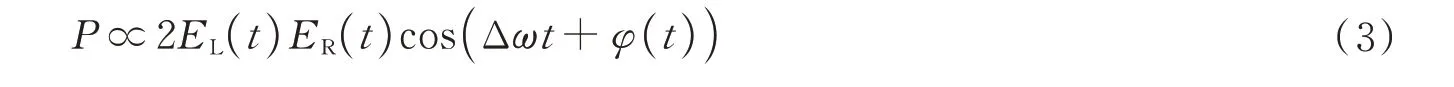
式中，φ(t)=φR(t)-φL(t)。

DAQ采集到的数字信号可以通过正交（I/Q）解调算法［20］得到信号的幅值。

2 φ-OTDR系统信号识别

2.1 小波包分解原理

φ-OTDR系统在实际应用中采集的信号往往具有冲击性和突变性，信号在时域上的波形变化剧烈，信号中的频率成分复杂，呈现出非平稳性的特点。小波包变换可以对信号按照频率特性逐层分解，从而充分表征不同信号的特性［21-22］。信号的三层小波包分解如图2所示，信号S0，0分解为S1，0和S1，1，S1，0和S1，1分别进一步分解为S2，0和S2，1，S2，2和S2，3，以此类推，逐级分解。

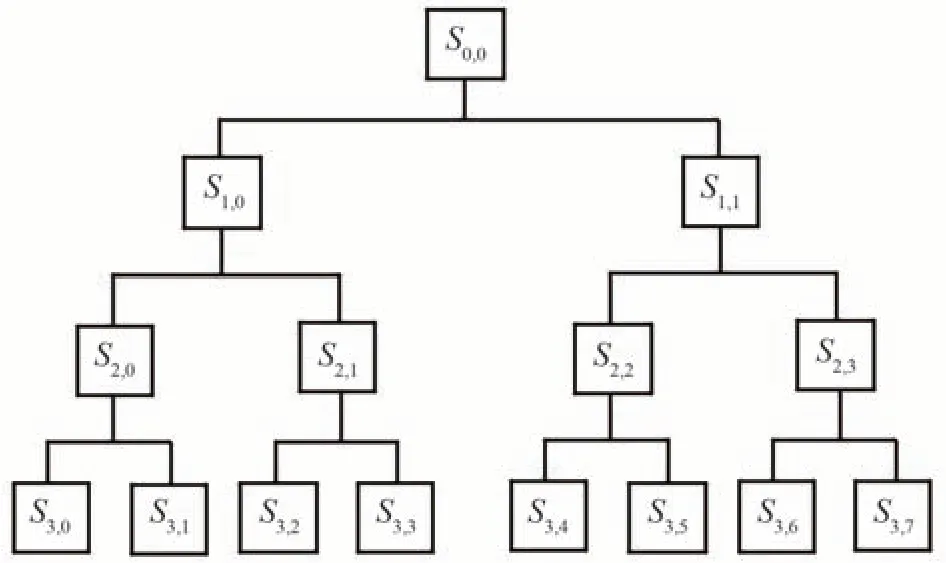
图2 三层小波包分解Fig.2 Three-layer wavelet packet decomposition

信号S0，0经过N层小波包分解之后可以表示为

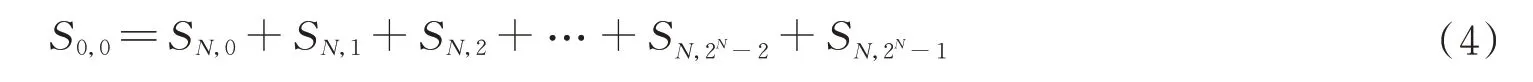
式中，SN，0，SN，1，SN，2，…，SN，2N-2，SN，2N-1表示S0，0经过N层小波包分解后的子频带，当信号的采样率为f，则第j个频带的频率范围为(j+1)，j=0，1，…，2N-1。各子频带的能量计算公式为

式中，dNj是第N层第j个频带内的小波包分解系数。将各子频带的能量进行归一化，得到特征向量[λ1，λ1，…，λ2N]为

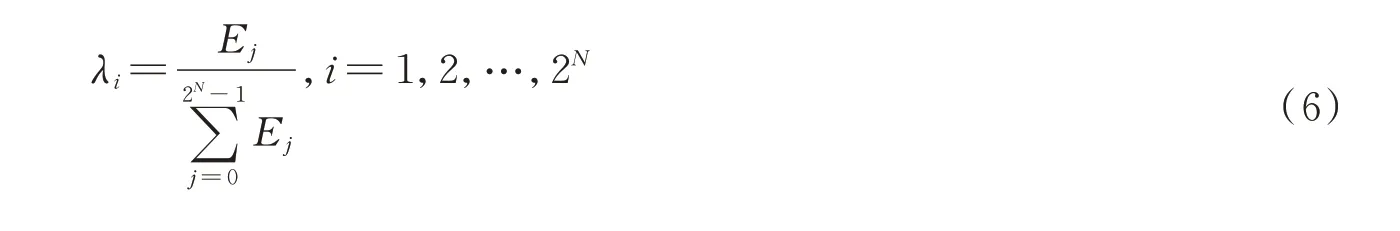
2.2 SVM分类原理

SVM在处理小样本、非线性问题分类时具有极好的性能；其核函数构造简单，泛化能力强，且计算速度较快。对于一个给定的样本集T={(xi，yi)，i=1，2，…，N}，xi∈Rn，yi∈{-1，1}，分类决策函数为［23］

2.3 性能评估指标

SVM是一种有监督学习模型，信号识别的结果可以用混淆矩阵描述。图3是二分类的混淆矩阵示意图，主对角线是正确的分类结果。本文采用准确率、精确率、召回率和F1值四种性能评估指标对分类效果进行评价。

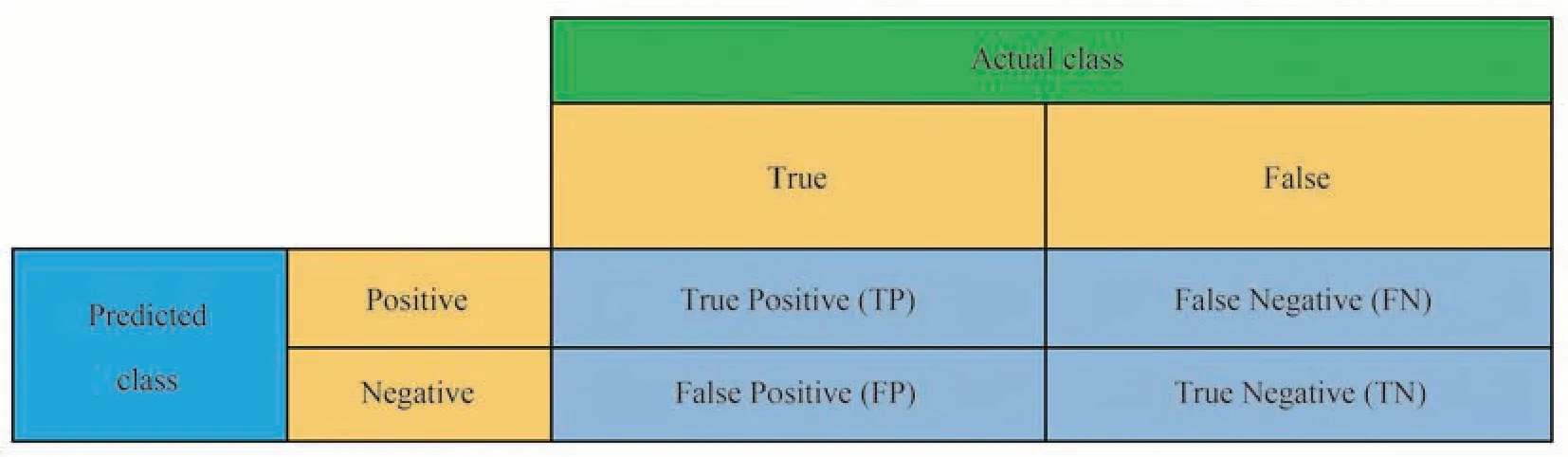
图3 二分类混淆矩阵Fig.3 Binary confusion matrix

准确率（Accuracy）是所有样本中正确分类的个数占总样本的比例，计算公式为

精确率（Precision）是某种模式中预测正确的样本占所有预测为该模式样本的比例，召回率（Recall）表示某种模式预测正确的样本占所有实际为该模式样本的比例，两者的计算公式为

由于精确率和召回率之间往往呈负相关关系，因此可以通过F1值让两者达到一个平衡的关系，F1值的计算公式为

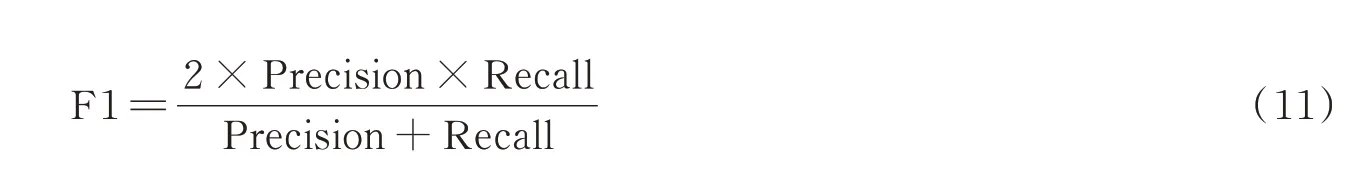
3 实验结果与讨论

3.1 信号采集

实验分别采集敲击、晃动、行走情况下的扰动信号和环境中的噪声信号，共采集800组实验数据，每种信号各200组。其中敲击信号是在光缆上铺一块木板，并使用一个直径约为3 cm的铁棒对木板进行敲击来模拟应力破坏，木板覆盖的光缆长度为1 m；晃动信号是将一段3 m长的光缆悬挂起来晃动来模拟攀爬；行走信号由一个人以一定频率在光缆上踩踏，作用长度为0.5 m；噪声信号则是在光纤没有外界干扰的情况下采集普通环境下的信号。每个事件样本信号时长为0.5 s，系统监测光缆距离为2.3 km。实验环境如图4所示。

图4 实验环境Fig.4 Experimental environment

振动事件多存在于低频带，对采集的信号进行频谱分析发现，扰动信号的频谱能量主要集中在800 Hz以内，因此，脉冲重复频率设为2 kHz；DAQ每次采集1000条拍频信号曲线。通过移动差分法定位扰动信号位置，三种扰动事件的定位结果如图5所示。敲击、晃动、行走事件的扰动信号峰值幅度分别在2200 m，2230 m，2170 m。

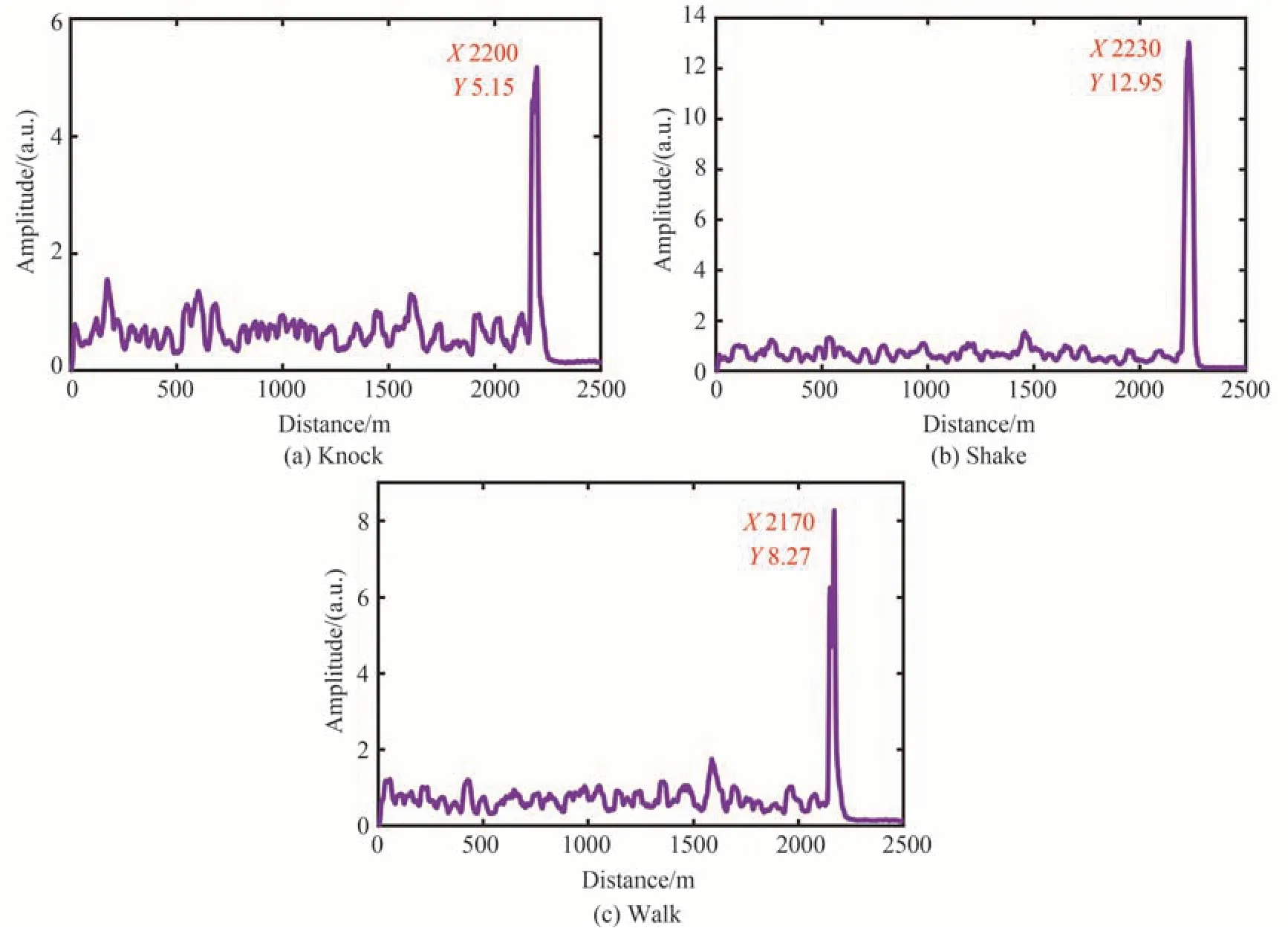
图5 三种扰动信号的定位结果Fig.5 Location results of three disturbance signals

由于不同信号的幅值数量级相差较大，为了增强不同信号之间的对比性，本文采用Max-Min归一化对数据进行处理，Max-Min归一化公式为

式中，xmax表示信号的最大值，xmin表示信号的最小值。

四种信号归一化后的典型时域波形如图6所示，分别是敲击、晃动、行走和噪声。不同事件的信号波形有明显不同，其中，敲击信号的持续时间最短而晃动信号的持续时间较长；两种信号的幅值均随着时间推移呈现衰减的趋势；与敲击信号相比，晃动信号的幅值的衰减趋势更均匀。行走信号的幅值与敲击和晃动信号的幅值相比略低一些，并且在中间0.25 ms～0.3 ms内的一小段时间幅值降低后又升高；三种扰动事件的信号幅值均变化较大。与扰动事件信号相比，噪声信号归一化后的幅值较小且强度分布均匀，没有产生明显的变化。

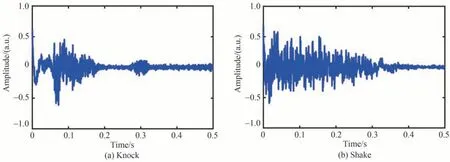
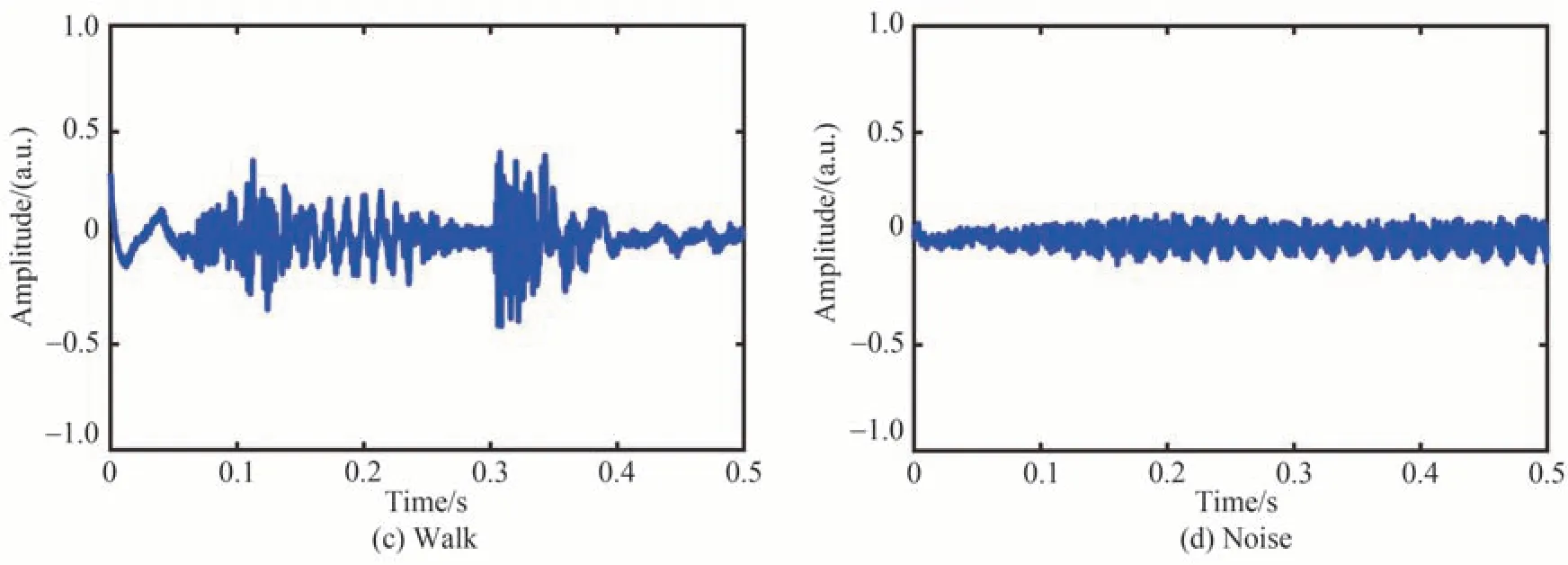
图6 四种不同信号的典型时域波形Fig.6 Typical time domain waveforms of four different signals

3.2 信号识别

小波基函数具有多样性，不同的小波基函数对信号的处理结果差异较大。本文采用Dmeyer小波基。Dmeyer小波具有良好的正交性和紧支撑性，保证了信号的时间特性且各频带信号之间不会相互影响产生混叠，并且收敛速度较快。在对信号进行小波包分解时，分解层数越大，频带分辨率越高，但过大的分解层数会造成误差，计算复杂度也会越高；因为小波包分解的计算复杂度O（n）由分解步长n决定，n与小波包分解层数正相关。本文在综合计算复杂度和准确性的基础上，根据对实验数据的验证结果，最终选择Dmeyer小波基对信号进行三层小波包分解，可以充分反映不同事件的信号特征。四种信号的典型小波包能量谱如图7所示。

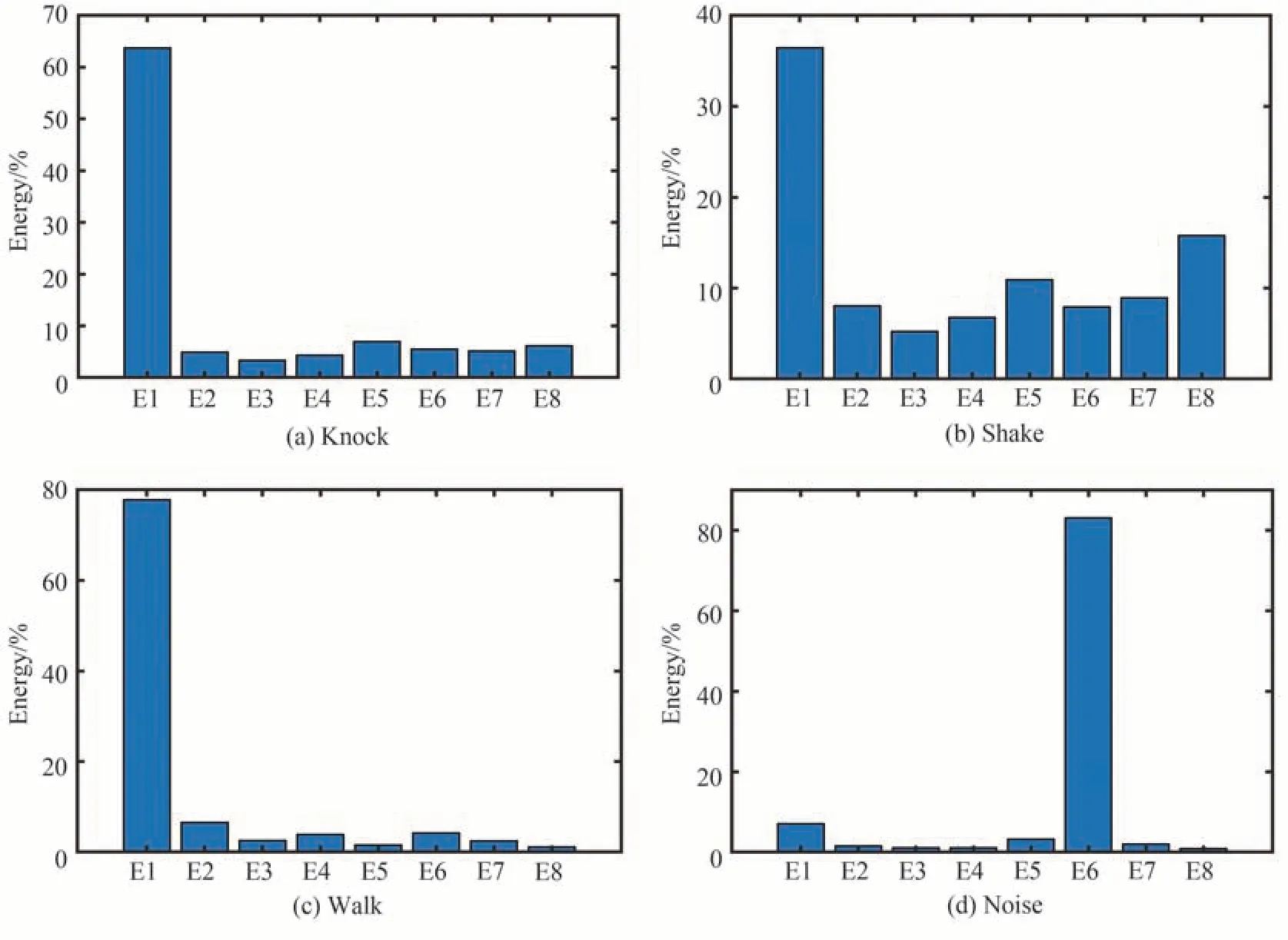
图7 三层小波包分解典型能量谱Fig.7 Typical energy spectrum of three-layer wavelet packet decomposition

从图7可以看到，三种扰动事件信号中，敲击信号和行走信号，频谱能量主要集中在第一频带，远高于晃动信号在第一频带内的能量占比，但两者在中高频带的能量分布有明显差异；敲击信号在中高频带内的能量分布呈现一种平稳的趋势，从第二频带到第八频带内的能量占比相差较小；行走信号则在中高频带内的能量分布整体呈现下降趋势，且衰减速度较快。晃动信号虽然在第一频带内的能量占比最高，但在中频和高频带内也均有较高的能量分布，在中高频带内的整体能量分布较均匀。噪声信号的能量主要集中在第六频带，这是因为噪声信号通常都是高频信号。

对800组信号进行三层小波包分解并将同一事件信号的能量特征向量进行算术平均，不同信号的小波包平均能量分布如图8所示。从图8中可以看到，噪声信号的平均能量分布与其余三种扰动信号的平均能量分布有明显不同；噪声信号的能量主要集中在第六频带，敲击信号、晃动信号和行走信号的能量则均集中在第一频带，这是因为扰动信号多为低频信号；但行走信号在第一频带的能量占比要高与敲击和晃动信号，这是因为行走时的频率较低。其中，敲击信号和晃动信号在高频带内的能量占比有些相似。由于不同信号的平均能量分布存在差异，因此小波包能量谱可以有效用于信号识别。

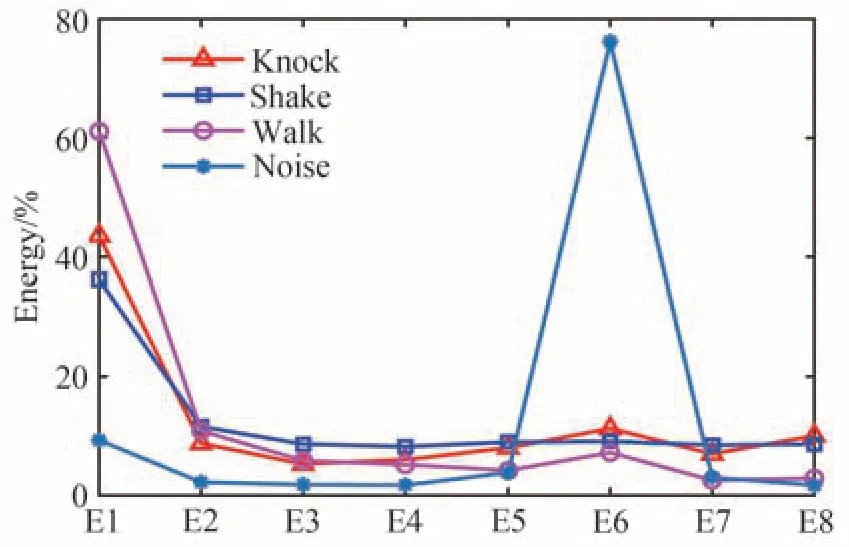
图8 四种不同事件的信号平均能量分布Fig.8 Average energy distribution of four differrent events

对采集的800组信号进行数据集划分，其中，每种事件随机选取150组，共600组信号作为训练集，剩余200组信号作为预测集。输入样本是信号经过三层小波包分解后的8维能量特征向量，SVM的分类结果如图9所示。其中，敲击和晃动两个信号的识别有一些偏差，2个敲击信号被识别为晃动信号，3个晃动信号被识别为敲击信号，这与它们在高频带内的能量分布相似有关。敲击信号的识别精确率、召回率和F1值分别为94.12%、96%和95.05%；晃动信号的识别精确率、召回率和F1值分别为95.92%、94%和94.95%；行走信号和噪声信号的识别精确率、召回率和F1值均为100%；识别总体准确率在97%以上，对扰动信号的识别准确率优于基于STFT的CNN［12］和基于HOS的LSVM［15］。实验结果显示，基于小波包分解和SVM的样本训练时间和测试时间分别为7 ms和3 ms，信号识别实时性较好。

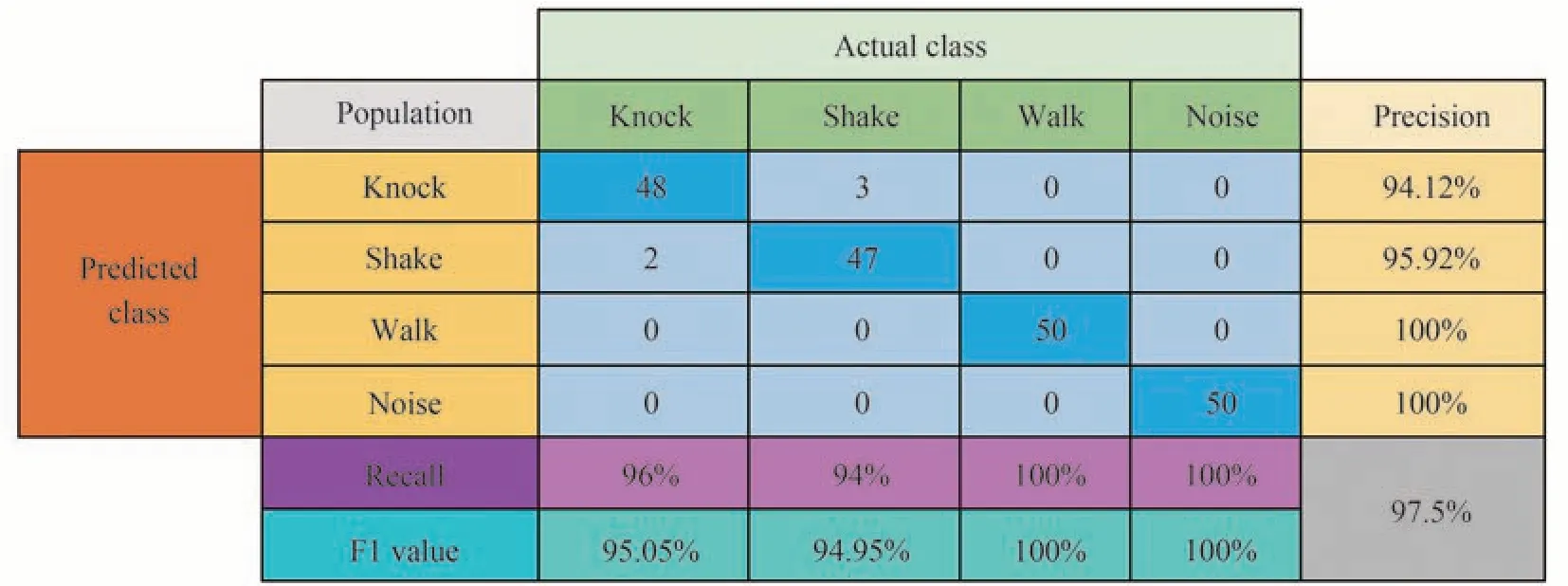
图9 SVM信号识别结果Fig.9 Signal recognition results of SVM

4 结论

本文针对φ-OTDR系统的信号识别问题，提出一种基于小波包分解和SVM算法的信号识别方法。通过对不同事件的信号进行小波包分解获得能量特征向量作为SVM的输入样本；对现场采集的800组实验数据进行训练和预测，并通过多种性能评估指标对识别效果进行评价。实验结果表明，小波包能量谱能够表征不同信号的特征，可以有效应用于φ-OTDR系统的信号识别。其中，敲击信号和晃动信号的识别精确率、召回率和F1值分别为94.12%、96%、95.05%；95.92%、94%、94.95%；行走信号和噪声信号的识别精确率、召回率和F1值均为100%；总体识别准确率在97%以上。该方法能够较好地识别不同类型的事件信号，具有较高的实时性和准确率，为φ-OTDR系统的推广应用提供了有益的参考。