封闭式建筑群内天然气管道泄漏扩散特性研究

梅 苑，帅 健，任 飞

(中国石油大学(北京)安全与海洋工程学院，北京 102249)

随着世界能源结构的调整，城市天然气管网迅速发展。天然气管网的建成给人们的生活及生产带来了巨大的便捷，但也带来了相应的安全隐患[1-2]。如：2010年9月9日，加利福尼亚州圣布鲁诺天然气管道发生破裂事故，事故后果造成维护费用高达1 350万美元；2018年6月10日，中缅天然气输气管道发生泄漏燃爆事故，造成1人死亡、23人受伤，直接经济损失达2 145万元。因此，从安全角度来看，对于天然气管道泄漏扩散规律的研究具有重要意义。

现场试验、风洞试验和数值模拟方法是研究气体泄漏扩散的重要手段，多年来学者们基于以上方法对可燃气体泄漏扩散特性展开了大量的研究工作。如：Krogstad等[3]通过风洞试验研究了重气连续泄漏后矩形建筑物对重气云羽扩散的影响，结果发现重气云羽扩散时出现分叉现象，且建筑物底部产生的漩涡将会减小其周围的重气浓度，对重气云羽的扩散造成了极大的影响；Konig-Langlo等[4]通过风洞试验对比了瞬时泄漏源与连续泄漏源在稳定大气流动和湍流条件下对重气扩散的影响，证实了重气密度比对其扩散起次要作用，并得到不利大气条件下重气可燃距离的计算方法；Cowan[5]模拟了简单建筑物侧面发生气体泄漏的情况，并将数值模拟结果与风洞试验结果进行了对比分析；张甫仁等[6]利用计算流体力学(CFD)软件对建筑物群外空间内城市燃气连续泄漏扩散过程进行了数值模拟，对比分析了环境温度、湿度对燃气泄漏扩散的影响和浓度场的变化规律；高炜等[7]借助高斯扩散模型研究了不同大气环境下天然气管道泄漏扩散的危险范围，结果发现提高风速会显著降低对天然气管道泄漏事故后果的影响；周宁等[8]采用fluent平台针对不同风速下丁烷泄漏扩散过程进行了数值模拟研究，结果发现风速增大有利于减小丁烷高浓度区域的面积，从而减小事故危害。

目前，学者们针对气体泄漏扩散的试验研究大多采用缩比性试验平台，较难实现大空间场地内天然气泄漏扩散过程的研究，而在使用模拟方法时忽略了CFD软件在流场预测方面的潜力，仅从气云的表象变化展开分析。鉴于此，本文基于CFD软件对不同风速下天然气管道泄漏扩散过程进行了数值模拟研究，重点研究了风速作用下建筑区内流场变化特性对于天然气气云扩散的影响。

1 数值建模和工况设置

1.1 控制方程

Fluent软件在气体泄漏扩散模拟仿真过程中设置了更多的监测点，可使测量数据更为全面、有效[9-11]，部分学者[12-14]通过试验验证了其在天然气管道泄漏扩散预测方面的可靠性，因此本文采用Fluent软件作为研究手段。利用Fluent软件进行模拟计算时需要将扩散气体的质量、能量等守恒方程作为控制方程，并利用Realizablek-ε湍流模型和组分运输模型来模拟气体泄漏扩散过程。在流体力学中流动运动的连续性方程、动量方程和能量守恒方程可通过统一的方程表示如下[15]：

(1)

式中:φ代表某一变量；Γ表示流体的扩散系数；S表示源项；Γ和S均对应特定的变量φ。

公式(1)从左到右的4项分别为时间项、对流项、扩散项和源项，取不同的φ、Γ和S，则可得到相应的连续性方程、动量方程和能量方程。

1.1.1 湍流动能方程

Realizablek-ε湍流模型比标准k-ε湍流模型在浓度分布上有更好的精度。对气体泄漏扩散湍流问题采用Realizablek-ε湍流模型，模型中k和ε方程如下：

k方程为

(2)

ε方程为

(3)

式中：μt为湍动黏度(kg·m·s)；E为时均应变率(%)；ρ为流体密度(kg/m3)；ui为时均速度(m/s)；xi为控制单元体长度(m)；k为湍流动能(J)；ε为湍流动能耗散率(%)；C1、C1ε、C3ε为3个常量；σk=1.0，σε=1.2，C2=1.9；Gk为因速度梯度产生的湍流动能源项；Gb为因浮力产生的湍流动能源项；YM为在可压缩湍流中波动扩张引起的耗散项；θ为运动黏度(m2/s)。

1.1.2 组分运输方程

组分运输方程如下：

(4)

式中：u、v、w为流体速度分别在x、y、z轴上的速度分量(m/s)；mi为不同组分所占的质量比例；Γi为湍流扩散系数。

1.2 模拟工况设置

本文模拟了5种风速条件下天然气管道泄漏扩散过程，模拟工况设置的详细信息见表1。

表1 模拟工况设置信息

1.3 数值模型建立与参数设置

从对气体泄漏扩散影响的角度来看，建筑物的布局方式可分为封闭式、斑块式和街道峡谷式，而封闭式的建筑物排列方式不仅在城区中最为常见，也是对气体泄漏扩散影响最大的建筑物布局方式[16]。因此，本文在计算域中加入封闭式建筑物排列。为了保证计算域内流场充分发展，减小边界层对流场发展的影响，计算域的尺寸需尽可能大，但这也相应地增加了计算成本。根据阻塞率原则(即建筑群的阻塞率应≤3%)，本文确定计算域的空间尺寸为530 m×380 m×150 m(x，y，z)，建筑物的尺寸为15 m×30 m×30 m(x，y，z)，此时阻塞率为2.3%，满足阻塞率原则，建立的封闭式建筑群内天然气管道泄漏扩散的物理几何模型， 见图1。天然气与环境温度均设置为296.3 K，环境压力设置为标准大气压。天然气管道泄漏口设置于建筑群空腔区内，为直径为105 mm的圆形泄漏孔，其边界条件设置为质量入口边界。泄漏的天然气管道管径为200 mm，运行压力为0.35 MPa，属于中压输送水平。利用大孔泄漏计算模型[17]得出泄漏孔径为105 mm条件下天然气管道泄漏速率约为5.0 kg/s。风入口面及出口面的边界条件分别设置为速度入口、压力出口；地面及建筑的边界条件采用壁面边界条件；其余边界条件皆采用对称边界条件。采用PISO算法对压力场和速度场进行耦合，对流项离散采用二阶逆风格式，扩散项采用二阶中心差分格式。

图1 封闭式建筑群内天然气管道泄漏扩散的物理几何模型

1.4 网格划分与模型验证

本文借助ICEM软件对计算域进行结构化网格划分，从而提升整体网格质量。针对建筑区及泄漏源附近的网格进行局部加密，但网格数量过大，会导致计算成本增加。因此，本文共划分4组数量梯度的网格来分析验证模型的独立性，网格数量依次为145万、198万、241万和296万，并将各数量梯度网格模拟计算结果与试验数据[16]进行了对比(见图2)，结果发现：随着天然气泄漏时间的增加，因网格数量产生的计算误差会逐步拉大，且当网格数量达到241万和296万时，网格数量对天然气气云扩散范围和浓度分布的影响较小，可以达到较高的计算精度。因此，考虑到计算成本，最终确定计算网格数量为241万。

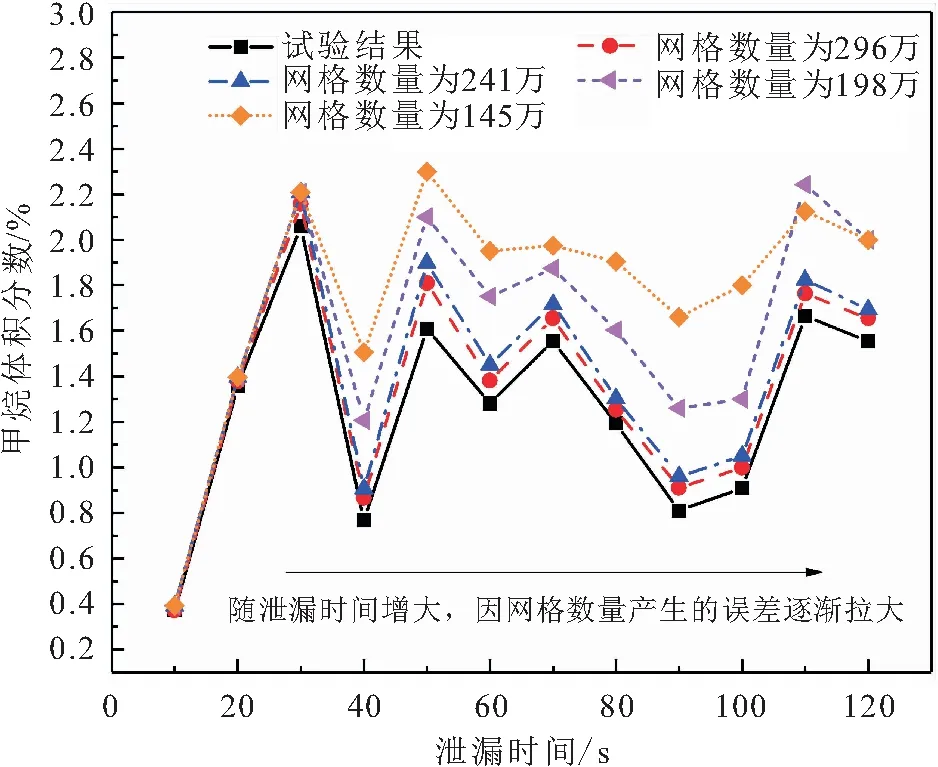
图2 不同风格数量模拟结果与试验结果的对比

2 数值模拟结果与分析

2.1 封闭式建筑群风场模拟

风场的发展会直接影响天然气管道泄漏事故后果。为了获得可靠的预测结果，本文采用两步模拟的方法，即首先进行风场模拟，预算300 s，以便获得较好的风场初始值；然后开启泄漏源，进行天然气管道泄漏事故后果模拟。大气流动是一种复杂的湍流运动，大气边界层的流动特性通常采用平均风廓线和湍流参数来描述。根据Davenport的实测数据[18]，采用幂律方程来描述入流边界处的风速分布，即：

(5)

式中:z0为参考高度(m)，取10 m；z为距离地面的高度(m);α为地面粗糙度指数；v0为距离地面10 m高度处的平均风速(m/s)，文中提及的风速皆指距离地面10 m高度处的平均风速；vz为距离地面高度z处的平均风速(m/s)。

如图3所示，本文选取10 m高度处风速为6 m/s时计算域内风场发展情况进行分析。

图3 建筑物影响下的风场中风速分布云图(风速v为6 m/s)

由图3可见，建筑群的存在会极大地影响风场中风速的分布情况。在图3(a)中，风速随高度形成速度梯度，由于建筑物及大气湍流特性的影响，整个风场的风速梯度呈现一种不均匀分布；另外结合图3(b)可以发现，建筑物的迎风面会形成速度滞留区(如红色实线矩形框所示)，风速大幅下降，而在建筑物的背面则会形成低速回流区(如红色虚线矩形框所示)，此时气流形成反向运动。对应的流场变化为风速分布情况的分析提供了依据。图4为计算域内建筑物影响下的流场变化情况。

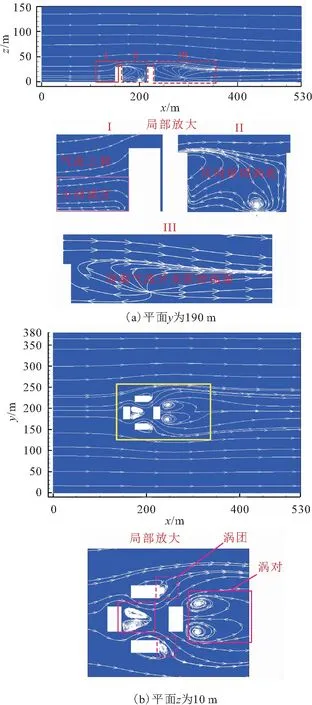
图4 建筑物影响下的流场变化图(风速v为6 m/s)

由图4可见，建筑的阻塞作用使得风从建筑物侧方及顶部进行绕流，形成反向运动的涡流，导致低速回流区的形成。本文选取图4中典型的特征区域流场进行了局部放大分析。在图4(a)中，当风与建筑物相遇时，在建筑物底部形成一个小回流区，由此往上气流沿建筑物“爬上”顶部与主流相遇汇合，造成速度梯度上移，形成速度滞留区[见图4(a)-Ⅰ]；当风离开建筑物顶端时，部分气流脱体朝斜下流动折回地面，在建筑物空腔内产生与风速相反的反向封闭涡旋，促成低速回流区I形成[见图4(a)-Ⅱ]；建筑物顶端气流并未折回地面形成反向涡流[图4(a)-Ⅲ]，由此可知顶部气流运动并非是低速回流区Ⅱ形成的主要原因。在图4(b)中，风侧向绕过建筑物在背风面形成的反向涡团及涡对是低速回流区形成的重要因素；而风在离开建筑群后，流线恢复正常，风的运动也趋于稳定。

2.2 天然气管道泄漏初期天然气泄漏扩散特性模拟

10 m高度处风速为6 m/s条件下天然气管道泄漏初期天然气气云扩散云图，见图5。

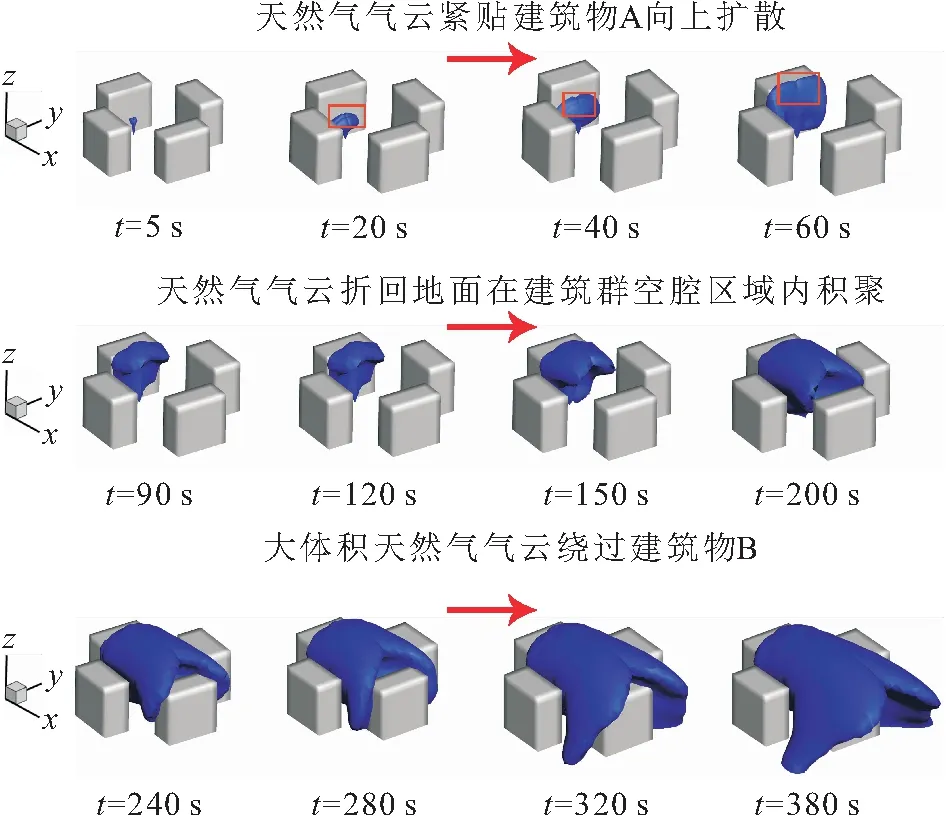
图5 天然气管道泄漏初期天然气泄漏扩散云图(甲烷浓度为1%，风速v为6 m/s)

建筑物作为天然的障碍物，使得空间中的风场需要绕流而行，从而导致建筑物背面及建筑群空腔区域内形成湍流涡，影响天然气气云的扩散传播。由图5可见：当天然气管道发生泄漏时，由于Coanda效应，天然气气云首先紧贴建筑物A向上扩散，且在天然气气云上升过程中，侧向绕流形成的涡会影响天然气气云发展的结构，天然气气云顶部逐渐形成分叉结构(如红色矩形框所示)；在泄漏时间t为90 s，当天然气气云抵达建筑物区域A顶端时，由于建筑物顶端风场绕流的作用，天然气气云开始平行向下风口传播，另外建筑群空腔区域内的反向涡旋迫使天然气气云在下风口传播过程中折回地面，并在建筑群空腔区域内积聚；随着天然气在建筑群空腔区域内积聚，天然气气云体积不断增大，最终在风场的作用下，建筑群空腔区域内的天然气气云团将从建筑物B的侧面及顶端绕行通过。

2.3 天然气管道泄漏后期不同风速下建筑群内天然气气云积聚效应模拟

天然气管道泄漏后期(泄漏时间t分别为500 s、550 s和600 s时)在顺风向扩散距离内不同风速下天然气浓度(体积分数)分布及气云形状变化，见图6。其中，天然气泄漏扩散云图中的天然气气云浓度边界为1%，天然气气云颜色表示x轴向速度。

当泄漏时间为500 s时，由图6(a)可以明显看出随着下风口距离的增加，天然气浓度逐渐降低，但在建筑群空腔区域内及建筑物B背风面附近，大风速条件下天然气浓度明显高于小风速条件，如在距离泄漏源为56.5 m处(即x=200 m时)，风速为2 m/s条件下该距离处天然气浓度为10.23%，而风速为10 m/s条件下该距离处天然气浓度却能保持在18.81%，高于前者83.87%。结合对应的天然气泄漏扩散云图对上述现象进行分析，发现：当风速较小时(风速为2 m/s)，天然气气云从建筑物顶端通过建筑区沿下风口飘散，天然气气云整体颜色分布均匀，表示天然气气云在x轴向速度大体保持一致，稳定在2～4 m/s范围内；而随着风速的提高(风速为6 m/s)，在建筑群空腔区域内，由于建筑物A顶端形成的反向涡旋导致天然气气云下沉，在建筑群空腔区域内积聚，之后天然气气云开始绕过建筑物B向下风口传播。而由上述风场分析可知，建筑物B背风面在风场作用下形成了规模较大的涡对，对天然气气云产生较强的卷吸作用，导致天然气气云在建筑物B背风面发生二次下沉、积聚。通过分析天然气气云颜色分布可知，天然气气云整体产生较大的速度差值，下沉部分天然气气云x轴向速度较低，维持在3 m/s，而天然气气云上端仍保持较高的扩散速度，达到12 m/s左右。而当风速进一步增大时，即风速为8 m/s、10 m/s时，天然气气云将会牢牢地积聚在建筑群空腔区域内，停止向下风口扩散。与风速为6 m/s时相比，天然气气云上端x轴向速度及分布范围都相应减小，保持在9 m/s。这是因为：大风速条件下建筑群空腔区域内及建筑物B背风面的涡团发展规模将会进一步增大，涡能更高，对于天然气气云的积聚效应也会更好，天然气气云整体受到更强的减速效果。

图6 天然气管道泄漏后期不同风速下建筑群内天然气气云积聚效应(甲烷浓度为1%)

不同风速下建筑区背风面涡团发展规模，见图7。

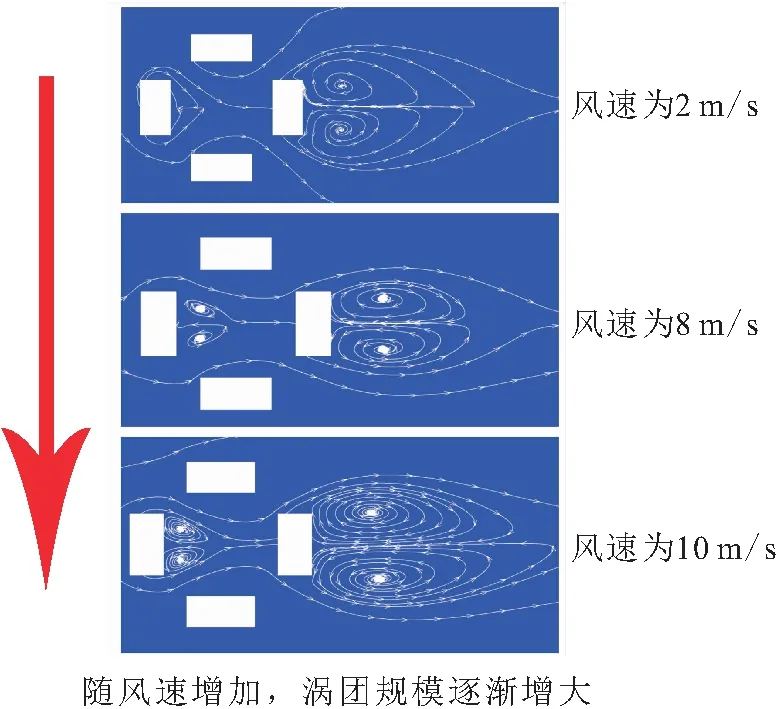
图7 不同风速下建筑区背风面涡团发展规模

当泄漏时间达到550 s时，由图6(b)可知虽然天然气气云的扩散形状并未发生明显改变，但不同风速下建筑群空腔区域附近的天然气浓度差距变得更加显著，远距离处天然气浓度略有上升(如红色实线框所示)，说明随着泄漏时间的延长，小风速条件下(风速为2 m/s、4 m/s)天然气气云仍会持续向下风口传播；当泄漏时间为600 s时，由图6(c)可知除天然气浓度差异明显外，天然气气云积聚作用的影响区域也在扩大，当泄漏时间由500 s延长至600 s时，积聚区Ⅱ的x轴向最远范围由x=300 m扩张至x=350 m。

综上分析可知，风速的提升会加剧建筑群区域内天然气气云的累积。

3 结 论

(1) 本文使用UDF(用户定义函数)在Fluent软件中对不同高度的平均风速与湍流参数进行了修改，并采用两步模拟的方法，对风场进行了预先计算，获得了稳定的风场初始值。建筑物作为天然的障碍物，使得空间中的风场需要绕流而行，导致建筑物背风面及建筑群空腔区域内形成湍流涡，影响天然气的泄漏扩散。

(2) 在天然气管道泄漏初期，建筑群空腔区域内，气流顶端绕行形成的反向封闭涡旋导致天然气气云在建筑群空腔区域内积聚。随着天然气气云在建筑群空腔区域内积聚，天然气气云体积不断增大，最终在风场的作用下，建筑群空腔区域内的天然气气云将从建筑物B的侧面及顶端绕行通过。

(3) 在天然气管道泄漏后期，建筑群与风场作用下流场运动对于天然气会产生积聚作用，随着风速的增大，绕流形成的涡团规模逐渐增加，其卷吸效果也逐渐增强，导致天然气气云整体在建筑区附近发生下沉。因此，天然气管道泄漏事故发生时，根据风速条件和泄漏源附近的居民建筑物分布情况，可以判断事故的主要影响区域及其严重程度，从而制定合理的应急预案。

(4) 随着泄漏时间的延长，小风速条件下(风速为2 m/s、4 m/s)天然气气云仍会持续向下风口传播；而大风速条件下(风速为6 m/s、8 m/s、10 m/s)天然气气云仍大量积聚于建筑群区域内，建筑物B背风面的积聚区Ⅱ范围略微扩大，当泄漏时间由500 s延长至600 s时，该积聚区Ⅱ的x轴向最远范围由x=300 m扩张至x=350 m。