凹槽结构对飞机制动盘制动过程中温度场和应力场的影响

于 洋，黄崇莉，汪 涛，潘晓阳，李 猛

(陕西理工大学机械工程学院，陕西 汉中 723000)

0 引言

制动器是飞机、汽车、高速列车等大型机械设备减速或刹车的关键部件，其中的盘式制动器的制动力高且稳定，其应用也越来越普遍。这些大型机械设备都具有转速高、制动惯性大等特点，在制动过程中具有非常大的水平速度，而气动阻力和轮胎与地面的摩擦阻力产生的减速作用却非常小，其余大部分动能都会被刹车装置转化为热能吸收掉。在一次制动过程中，刹车装置的温度可以从室温上升到几百甚至上千摄氏度，并且在刹车装置内部产生极大的温度梯度，由此产生的热应力对刹车装置的使用寿命产生很大程度上的影响[1-3]。

针对刹车装置温度场和应力场方面的研究，相比于国内，国外学者对这方面的研究比较早，相对更加成熟。美国学者Keddedy和Ling[4]在1974年首次使用有限元法对飞机刹车装置的不稳定热弹性问题进行了分析，并提出了一种可预测盘式制动器磨损率的准则；Qi和Day[5]采用热电偶法测量了摩擦界面的温度，并对摩擦界面温度的大小和分布进行了研究；P.Grzes[6]基于使用HDFW方程组，提出了一种计算反复制动过程中制动盘摩擦表面最高温度的方法；戴雁琴[7]基于对盘式刹车装置的瞬态温度场的研究，建立了飞机起落架制动盘的瞬态温度分析模型，通过对瞬态温度场的研究，找出了影响刹车装置热学性能的主要因素；杨肖等人[8]根据生物的生长特点设计了三种抑制升温、预防疲劳磨损的仿生制动盘，并通过仿真分析了在紧急制动工况下仿生制动盘的温度和应力分布特点，得出了仿生制动盘温度和应力下降的主要原因；王强等人[9]通过分析孔盘结构对制动盘温度场和应力场的影响发现打孔会对制动盘的温度场和应力场产生不利影响，会降低制动性能;Yashvardhan singh Chouhan等人[10]对两种不同摩擦衬片结构下的实心和通风盘式刹车器进行了热分析和静态分析，研究发现相比于实心圆盘，通风盘式具有良好的温度分布效果，且具有更好的散热效果。

大部分汽车和高速列车使用的都是单圆盘式刹车装置，而大部分飞机使用的都是多圆盘式刹车装置，本文以某飞机的刹车装置作为研究对象，对刹车副的结构进行了挖槽处理，利用有限元软件ABAQUS对处理后的模型的温度场和应力场进行了分析，并列出了求解所需要的相关理论，最后对仿真结果进行了总结。

1 制动盘的建模与计算

1.1 模型条件假设

为了尽可能地模拟实际制动工况，保证计算精度，提高计算效率，对制动盘有限元模型做如下假设：

(1)施加在制动盘上的压力为常数且均匀分布；

(2)制动盘均为各向同性材料；

(3)忽略热辐射产生的影响；

(4)制动过程中环境温度保持在定值20 ℃；

一是扶贫项目的建设周期和脱贫攻坚的时间要求难以统一。每个项目建设是有其自身特定的建设周期的，若要把各环节工作做细致，从科学规划、择优立项、精心设计、按期申报到建设实施、验收审计，有的长达2-3年，相应项目资金也需要跨年使用，存在政府要求的工作完成进度与项目实施时间难以对接的问题。同时，由于统筹整合资金体量大，短期内集中投入到贫困村和贫困户，很多项目仓促申报、立项导致制订方案时缺乏科学的决策依据，不符合农村实际，而且项目一经审批立项，也不能随意调整变动，造成项目难以实施。

(5)制动过程中车轮做纯滚动。

1.2 模型建立

多圆盘式刹车装置包括刹车静盘、刹车动盘、扭力管、刹车作动筒、刹车磨损指示销等，如图1所示。刹车盘由多个刹车静盘和刹车动盘组成，静盘与动盘相互交叉堆叠。静盘通过内花键安装于相对于起落架固定的刹车装置扭力管上，不会随着机轮转动，只可做轴向运动，而动盘通过外花键与轮毂相连，既可以随机轮转动也可以做轴向运动。

图1 多圆盘式刹车装置

制动盘采用刹车性能优异的碳碳复合材料，材料属性如表1所示，其中，碳碳复合材料的比热容与温度的函数关系拟合图如图2所示。

表1 碳碳复合材料属性

图2 刹车盘碳碳复合材料比热容与温度的函数关系拟合图

建模时为简化计算，提高计算效率，只选取两个静盘和一个动盘作为研究对象，动盘与静盘的结构参数见表2[14]。

表2 动盘与静盘的结构参数

本文使用CATIA建立制动盘数学模型，并对动盘进行两种凹槽处理，如图3所示，凹槽截面形状为矩形，宽度为10 mm，深度为5 mm，凹槽个数分别为4个和8个，且凹槽长边与动盘线速度方向夹角为90°。

图3 制动盘有限元模型

将建立好的模型导入到ABAQUS中进行装配和网格划分，如图4所示，光滑动盘与静盘装配成制动盘A，带有4个凹槽的动盘与静盘装配成制动盘B，带有8个凹槽的动盘与静盘装配成制动盘C。

图4 制动盘有限元模型的网格划分

1.3 热学参数、载荷和边界条件的确定

由热传导理论可得制动盘的导热微分方程为：

(1)

式中：ρ为密度，kg·m-3；c为比热容，J·(kg·℃)-1；T为温度，℃；t为时间，s；λ为导热系数，W·(m·℃)-1；Q为热生成率，W·m-3。当导热系数为常数且无热源生热时，(1)式可简化为：

(2)

式中：k为热扩散率，m2/s，热扩散率的大小反映了物体传递温度能力的强弱。为使导热微分方程存在唯一解，还需满足下列定解边界条件[14]。

边界上的温度分布与时间的函数关系：

T(x，y，z，t)=T0

(3)

热流密度q(r,t)为：

(4)

在刹车盘的所有外表面上存在热对流，有：

(5)

在刹车副的摩擦面上主要是热传导，有：

(6)

式中：f(r,t)为在时间t时刹车盘距圆心距离为r处所受的摩擦力，N；R为轮胎半径，mm；φ为轮胎压缩量，mm；vω(t)为飞机在时间t时机轮的刹车速度，m/s；λ为导热系数；T0为环境温度，℃；ni为界面i的法向单位向量；hi为界面i的表面换热系数，W·(m2·℃)-1；q为刹车盘吸收的热流密度，W·m-2。

根据实际工况，上侧刹车静盘受到轴向的制动压力，为738900 Pa，飞机刹车速度为270 km/h，通过计算可得刹车盘初始转速为120.52 rad/s，刹车时间为20 s，由于假设飞机制动盘的制动压力等为定值，因此飞机在制动过程中制动盘的旋转运动可近似视为匀减速运动。

2 温度场仿真结果与分析

2.1 光滑表面制动盘模拟结果与分析

图5为飞机在制动过程中制动盘出现最高温度时的温度分布云图。飞机在开始制动阶段，动盘与静盘接触部分由于相互摩擦产生大量热量，这些热量未及时向周围区域扩散，导致接触部分开始迅速升温，制动盘内部轴向的温度梯度迅速增大，而径向的温度梯度很小，非接触部分几乎无升温。随着制动过程的进行，动盘与静盘摩擦产生的热量越来越多，由于热传导的作用，热量开始由接触表面向制动盘内部传递，并且制动盘非摩擦区域会与空气发生对流散热，此时由于动盘与静盘相互摩擦产生的热流密度非常大，制动盘内部热传导传递的热量远大于制动盘与空气接触部分发生对流散热散失的热量，这导致了制动盘整体的温度仍在不断上升，在11 s时超过了1000 ℃。可以看出，在开始制动后15.21 s时制动盘的温度达到了最高点，为1049 ℃，最终，随着制动过程的进行，车轮的转速逐渐降低，动盘与静盘摩擦产生的热流密度逐渐减小，制动盘的温度在达到最高点后，动盘与静盘相互摩擦产生的热量小于制动盘与空气对流散热散失的热量，因此制动盘的温度在达到最大值之后会逐渐减小，在最后刹停时温度降到了989.2 ℃，相比于最高温度降低了5.7%。

图5 光滑表面制动盘温度分布云图

在动盘上沿径向方向选取八个节点，其制动过程中的温度变化趋势如图6所示。由于节点1位于刹车动盘外花键处，未与刹车静盘产生摩擦，故其温度变化相比其余节点更加平缓。飞机在制动过程中，制动盘受到的制动压力均匀分布，机轮做纯滚动运动，动盘上由内半径向外半径方向线速度越来越大，因此在外半径处产生的热流密度会大于内半径处，又因在最外侧和最内侧会与空气发生散热，最终会形成随着半径的增大动盘与静盘接触部分的温度呈现出先增大后减小的分布形式。温度最高点位置位于动盘与静盘接触界面靠近外径处，接触界面温度分布均匀，高温区域呈环状，沿外径和内径方向温度逐渐降低，由参考文献[15]可知，该分布状态与制动盘在制动过程中实际的温度分布状态基本一致。

图6 动盘径向节点温度变化趋势

2.2 带凹槽结构制动盘模拟结果与分析

图7中(a)和(c)为制动开始时的温度分布云图，可以看出，在制动刚开始时，制动盘B和制动盘C的整体温升程度类似，在动盘表面有凹槽的地方都出现了局部热点，且制动盘的最高温度集中在热点处，并伴随有较大的温度梯度。此外，制动盘C有更多的凹槽，使得开始制动阶段动盘表面温度分布相比于刹车盘A和制动盘B变得更加不均匀。随着时间的增加，动盘与静盘接触表面因摩擦产生的热量开始向制动盘内部扩散，制动盘整体温度不断升高，在6 s左右就已经突破了1000 ℃，动盘与静盘接触表面的温度分布也越来越均匀，但是制动盘的最高温度仍然集中在凹槽附近，且无论是沿径向还是轴向方向，制动盘的温度分布梯度都在不断增大。图7(b)和图(d)为开始制动后13 s时的温度分布云图，此时制动盘B和制动盘C的温度达到了最大值1234 ℃和1235 ℃，比没有凹槽结构的制动盘高了185 ℃，且最高温度始终位于凹槽附近。随着制动过程的进行，制动盘在达到最大温度后由于产生的热流密度逐渐减小，在某一时刻会低于制动盘与空气接触部分散失的热量，导致制动盘温度逐渐降低，在制动结束时制动盘B和C的温度降到了1094 ℃和1097 ℃，相比于最高温度降低了11.3%左右。

图7 带凹槽结构制动盘温度分布云图

在动盘表面沿旋转方向依次选取八个节点，它们在部分制动过程中的温度变化如图8所示。由图8可知，各节点温度呈现先升高后降低的变化趋势，各节点温度比较接近，温度梯度较小，但是由于凹槽结构的存在，节点4和节点5会与空气发生对流散热，导致其温度变化会有轻微波动且相对于其余节点温度会相对较低。

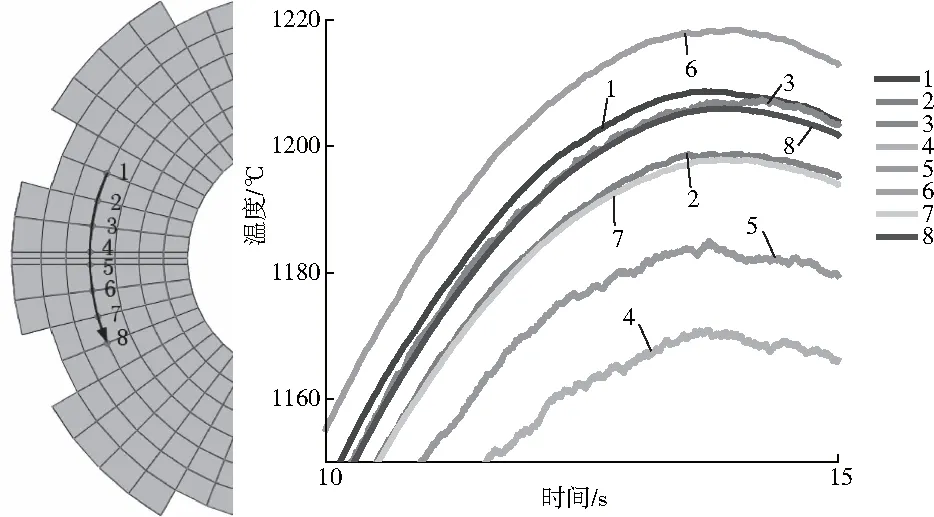
图8 带凹槽结构动盘表面周向节点温度变化趋势

2.3 凹槽结构对制动盘温度场的影响

图9为制动盘上最高温度节点处温度随时间变化的关系曲线，可以看出，带凹槽结构的制动盘B和C的温度始终高于制动盘A，最大温差在200 ℃左右。此外，在制动盘达到最高温度后，制动盘B和C的散热情况明显优于制动盘A。

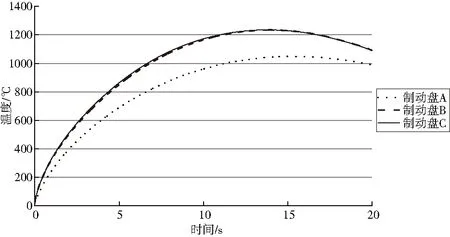
图9 不同结构制动盘最高温度变化曲线

3 应力场仿真结果与分析

在飞机开始制动时，三种不同结构制动盘的应力分布情况如图10中(a)、(b)、(c)所示，由于动刹车盘外侧花键与机轮相连，由机轮转动带动动刹车盘旋转，因此开始制动阶段动刹车盘的应力主要集中在外花键处，沿径向方向应力大小由外向内逐渐变小，其中带有凹槽结构的动刹车盘受到的最大应力位于凹槽处，并且随着动刹车盘上凹槽数量的增多，应力也会相应的增大，而且会在动刹车盘内部产生非常大的应力梯度。在制动阶段的中后期，三种不同结构的动刹车盘的应力分布情况如图10(d)、(e)、(f)所示，动刹车盘A内部的应力梯度逐渐变小，但是动刹车盘B和C内部的应力梯度依旧较大，较大的应力主要集中在动刹车盘的外花键处。制动盘B和C的应力分布情况类似，但是制动盘C的应力大小与无凹槽结构的制动盘A相近，由此可以判断制动盘上凹槽结构的数量与应力的大小并不是正相关。

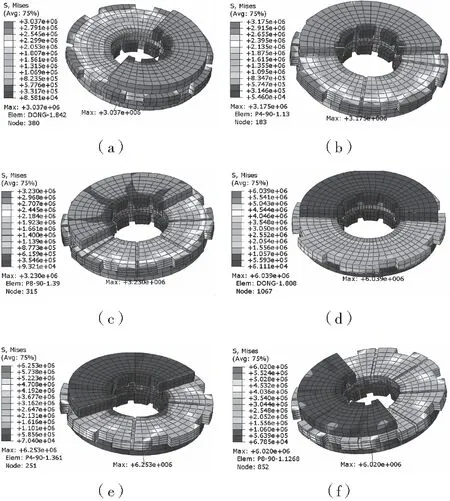
图10 不同结构制动盘应力分布云图

4 结论

根据飞机着陆时制动盘的工作特点，对比分析了制动盘有无凹槽结构对制动盘温度场和应力场的影响，得到以下结论：

1)制动过程中，制动盘温度在圆周表面呈环状分布，其大小沿径向方向由内向外呈现先增大后减小的分布形式。当制动盘带有凹槽结构时，制动盘的最高温度始终集中在凹槽附近。

2)凹槽结构会影响刹车盘在制动过程中承受应力的大小，制动盘B比制动盘A和C等效应力值大，制动盘A和制动盘C等效应力值基本一致。

3)相比于光滑表面制动盘，带凹槽结构的制动盘在制动过程中的温度会更高一些，最高温度的大小并不会随着凹槽数量的增多而增大。此外，凹槽结构有利于制动盘后期的散热，对制动盘的降温有着显著效果，为制动盘的加工制作提供了一定的参考。