基于小波变换的HEV复合电源功率分流控制策略*

牛晓燕，冯国胜

(1.河北工业职业技术大学，河北 石家庄 050091；2.石家庄铁道大学，河北 石家庄 050043)

0 引言

电源系统是并联混合动力汽车其中一个能量源，但是目前单一动力电池系统无法满足整车行驶过程中能量和功率的双重需求，因此在原有动力电池基础上增加了超级电容构成复合电源系统成为目前混合动力汽车电源系统的有效方案之一[1-2]。复合电源系统以动力电池作为主电源，以超级电容作为辅助电源，充分发挥超级电容充电快、寿命长、功率密度大的特点，从而与蓄电池联合实现比能量大、比功率大的高性能复合电源系统[3-5]。

复合电源系统能否发挥两种电源优势取决于采用的能量管理策略是否高效，目前常用的控制策略包括基于规则的控制策略、基于离线优化的控制策略、基于模型预测的控制策略和基于动态规划的控制策略等[6-8]。模糊控制策略虽然具有较好的鲁棒性，但无法保证全局最优，模型预测和动态规划策略在不能保证信息准确性的情况下，难以达到较好的实时控制效果。为获得更好的控制效果，国内外学者对复合电源系统能量控制做了大量研究。Kadri等人在新型的WT-DFIG/燃料电池/超级电容混合电力系统拓扑结构中采用了基于转矩控制回路的最大功率点跟踪算法[9]。Siangsanoh等人对复合储能系统提出了电流内环采用间接滑模控制的闭环控制方法，外环采用带干扰估计器的能量控制方法[10]。廖自力等人采用模糊控制算法实现电池荷电状态工作范围的优化控制的同时，设计了基于系统效率最优的负载需求功率分配策略[11]。王琪等人提出一种自适应滤波器功率分配控制策略，同时对该控制策略参数进行优化设计研究[12]。但上述控制策略仍然属于基于规则或是滤波控制方式，控制规则不能在线调整，且滤波控制策略中仅以电压作为功率的分配标准，均不能很好地适应动态工况。

为解决上述控制策略存在的问题、更好地发挥复合电源系统的性能，本文提出了基于Haar小波变换的复合电源功率需求分配策略，将分解得到的高频分量和低频分量分别分配给超级电容和动力电池，以匹配蓄电池和超级电容的不同性能，充分发挥超级电容“削峰填谷”的优势，减小蓄电池的瞬时电流冲击，实现复合电源系统能量优化控制，并利用Matlab/ADVISOR仿真环境下完成了复合电源系统搭建和功率分流策略二次开发，通过与逻辑门限值功率分流策略相对比，验证了小波变换功率分流控制策略的有效性。

1 复合电源模型

1.1 复合电源拓扑结构

图1为复合电源拓扑结构图，复合电源系统由动力蓄电池和超级电容构成，其中蓄电池与直流母线直接相连，超级电容经过被动式双向DC-DC变换器与直流母线相连，经逆变器后驱动电动机，直流母线采用小波功率分流控制策略对蓄电池和超级电容需求功率进行分解。直流母线电压由蓄电池直接决定，可对电机实现直接控制，超级电容通过DC-DC调节其端电压与蓄电池相同，有利于保护蓄电池，使其电压变化较平稳。

图1 复合电源拓扑结构图

1.2 动力电池模型

蓄电池模型选择Thevenin模型，该模型由三部分组成：理想电压源、欧姆内阻和一阶RC环节，其中一阶RC环节由并联电阻和电容组成，如图2所示。

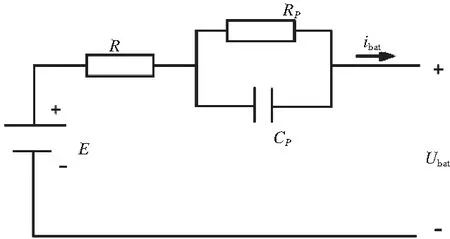
图2 蓄电池Thevenin模型等效电路图

根据基尔霍夫电压定律(KVL)，可得到蓄电池模型的数学表达式：

Ubat=E-IbatR-UC

(1)

(2)

式中，Ubat为蓄电池端电压(V)，E为蓄电池开路电压(V)，Ibat为蓄电池工作电流(A)，UC为一阶RC环节电压(V)，R为蓄电池欧姆内阻(Ω)，RP为极化电阻(Ω)，CP为极化电容(F)，ω为角频率。

蓄电池输出功率可表示为：

Pbat=Ubat×Ibat=(E-IbatR-UC)Ibat

(3)

式中，Pbat为蓄电池功率(W)。

联合式(1)、式(2)、式(3)可得蓄电池电流：

(4)

式中，Rbat为蓄电池内阻(Ω)：

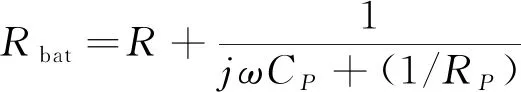
因此，蓄电池荷电状态(SOC，State of Charge)可表示为：

(5)

式中，SOCbat为蓄电池SOC，SOCbat0为蓄电池初始SOC，Cbat为蓄电池容量(Ah)。

1.3 超级电容模型

超级电容模型选择一阶RC模型，如图3所示。根据KVL，超级电容输出功率可表示为：

Puc=(Uuc-IucRuc)Iuc

(6)

式中，Puc为超级电容功率，Uuc为超级电容开路电压，Iuc为超级电容电流，Ruc为超级电容内阻。

超级电容电流为：

(7)

因此，超级电容SOC可表示为：

(8)

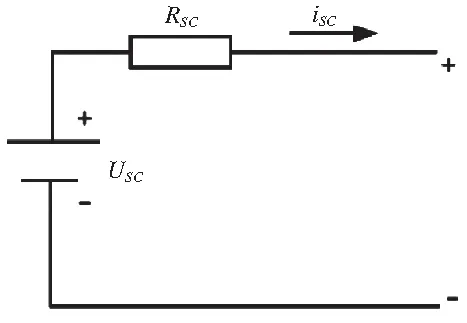
图3 超级电容一阶RC模型等效电路图

式中，SOCuc为超级电容SOC，SOCuc0为超级电容初始SOC，Cuc为单体超级电容容量(F)。

2 复合电源功率分流控制策略

复合电源系统用于满足混合动力汽车电机功率需求，其设计应充分发挥蓄电池和超级电容的各自特性。本设计中以蓄电池为主电源，提供电机的平均需求功率，以超级电容作为辅助电源，在混合动力客车起步、爬坡、加速、制动等大电流工况下工作，发挥“削峰填谷”的作用，满足瞬时功率需求，减少瞬时电流对蓄电池的冲击，从而延长蓄电池使用寿命。为对比说明基于小波变换的功率分流策略的有效性，本文分别设计了基于逻辑门限值的功率分流策略和基于小波变换的功率分流策略。

2.1 基于逻辑门限值的功率分流控制策略

基于逻辑门限值的功率分流策略的基本思路为，首先根据电机需求功率的正负来区分车辆处于驱动模式或者制动模式，之后将电机当前的需求功率与控制策略中设定的门限值进行比较，在考虑超级电容SOC的前提下，确定蓄电池和超级电容的需求功率，从而实现功率分流。

基于逻辑门限值的功率分流策略控制流程如图4所示。图中，Preq表示电机需求功率，Pd表示驱动状态门限值，Pb表示制动状态下门限值，SOCuh表示超级电容SOC上限值，SOCul表示超级电容SOC下限值，Pbat表示蓄电池需求功率，Puc表示超级电容需求功率，Fd(s)和Fb(s)分别为驱动和制动状态下的滤波函数。

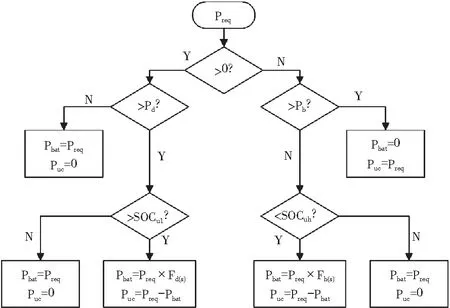
图4 逻辑门限值功率分流控制策略流程图

该控制策略中需根据循环工况采用平均功率对驱动功率和制动功率分别进行计算，得到逻辑门限值功率分流策略的门限值，并根据实际经验和超级电容的特性，设定超级电容的SOC上限值和下限值分别为0.9和0.2。

2.2 基于小波变换的功率分流控制策略

基于小波变换的功率分流控制策略以小波变换及其多尺度分解为理论基础，采用递推方式进行离散序列的多尺度分解，实现尺度空间的逐级分解，为复合电源系统功率分流控制策略提供依据。通过小波变换将电机对复合电源需求功率分解为不同频率带的信号，将低频分量分配给动力蓄电池，而将高频暂态分量分配给超级电容。

2.2.1 小波变换多尺度分解原理

根据小波多尺度分解概念，设ψj0,k(t)为小波空间Wj0的规范正交基，则此小波空间的原始信号可以表示为

f(t)=…+∑k∈zd-1,kψ-1,k(t)+

∑k∈zd0,kψ0,k(t)+∑k∈zd1,kψ1,k(t)+…

=∑j∈z∑k∈zdj,kψj,k(t)

(9)

且系数满足

dj,k=〈f(t),ψj,k(t)〉

(10)

式(10)称为正交小波变换，式(9)为其重构公式，也称为正交小波分解公式。

设φ(t)和ψ(t)分别为尺度空间V0和小波空间W0的规范正交基函数，可用V-1空间的规范正交基展开，即

(11)

(12)

式中，h[n]=〈φ(t),φ-1,n(t)〉，g[n]=〈ψ(t)，φ-1,n(t)〉。

对原始信号f(t)采用有限精度分解方案，则原始信号都可以表示为：

(13)

式中，cj，k—尺度系数，cj，k=〈f(t)，φj，k(t)〉；dj，k—小波系数，dj，k=〈f(t)，ψj，k(t)〉。

采用Mallat塔式分解算法使用数字滤波器形式对离散序列进行分解和重构，其系数计算公式为：

cj[k]=∑mh[m-2k]cj-1[m]

(14)

dj[k]=∑mg[m-2k]cj-1[m]

(15)

重构公式如下：

cj-1[m]=∑kh[m-2k]cj[k]+∑kg[m-2k]dj[k]

(16)

2.2.2Haar小波变换功率分流策略

Haar小波是具有对称性的正交紧支撑小波，且满足上述多尺度分解要求的正交小波变换，其便利性在于其小波变换和小波逆变换是相等的，其分解过程较其他小波简单[13]。本设计选择Haar小波进行功率分解，其小波母函数如下

(17)

按照前节分解原理，为保证基于哈尔小波的滤波器组具有正交性，选择二次采样方法，构造了基于三阶Haar小波的Mallat功率分解策略，利用Haar小波变换将原始信号分别通过低通滤波器H(ω)和高通滤波器G(ω)获得低频的概貌信号和高频的细节信号，从而实现复合电源系统功率需求信号的分解与重构。分解与重构示意图如图5所示。

在复合电源系统中，根据不同的充放电特性，蓄电池用于提供和吸收缓慢变化的功率，超级电容用于提供和吸收高频的瞬时变化的功率。因此经过图5的三次分解之后，将低频分量c3[k]从总的需求功率中分解出来，作为蓄电池的需求功率；将三次分解得到的高频分量d1[k]、d2[k]和d3[k]分解出来并进行求和，以此结果作为超级电容的需求功率。因此蓄电池和超级电容的需求功率表达式如下：

图5 小波功率分流控制策略信号分解与重构示意图

Pbat=c3[k]

(18)

Puc=d1[k]+d2[k]+d3[k]

(19)

3 仿真实验与结果分析

为验证复合电源系统分流控制策略的有效性，在Matlab/ADVISOR仿真环境下搭建复合电源系统，对提出的基于小波变换的功率分流控制策略进行仿真验证，具体的仿真模型如表1所示。选择中国典型城市循环工况作为测试工况，对基于小波变换的功率分流策略进行验证，并与逻辑门限值功率分流策略对比分析，仿真结果如图6所示。

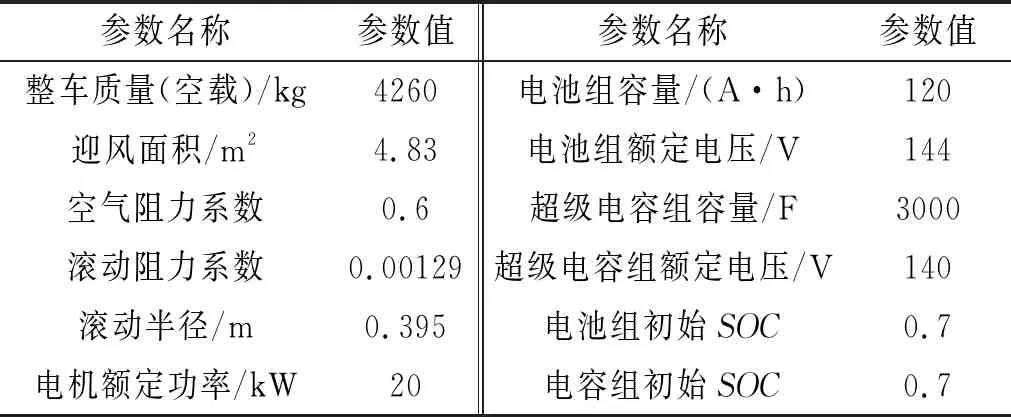
表1 仿真模型

图6(a)为整车在中国典型城市循环工况下的车速跟随曲线，说明采用复合电源系统供电，可以满足驱动电机的功率需求，实现整车按照指定工况行驶。

图6(b)为驱动电机需求功率，该功率中包含低频和高频功率，并且应全部由复合电源系统提供。图6(c)、图6(d)分别为不同功率分流控制策略下蓄电池和超级电容功率，两图对比说明在功率分流控制策略下，蓄电池承担了低频平均功率，超级电容承担了高频功率需求，同时电机需求功率中的峰值功率全部由超级电容承受，从而发挥了超级电容“削峰填谷”的作用，较好地保护了动力蓄电池。图6(c)中，采用小波功率分流策略的蓄电池功率数值虽略有增加，但是其功率波动明显低于采用逻辑门限值功率分流策略，这是因为小波功率分解策略侧重于对功率需求按照频率进行分解，目的在于降低高频功率对蓄电池的冲击，且小波功率分流策略下蓄电池充电功率有所增加，有利于保持蓄电池SOC平衡。在图6(d)中，小波功率分流策略下超级电容放电功率明显增加，从而解决了逻辑门限值功率分流策略下超级电容多数时间仅在制动能力回收时发挥作用的缺点，避免了蓄电池瞬时大功率消耗，有利于延长蓄电池使用寿命。

图6 复合电源功率分流策略仿真结果

图6(e)、图6(f)分别为蓄电池和超级电容电流，采用小波功率分流策略后蓄电池电流冲击频率明显降低，缓解了瞬时电流对蓄电池的冲击，部分工作点电流幅值虽有所增加，但整个行驶工况内最大充放电电流值几乎没有变化。超级电容工作电流经小波功率分流策略后，充放电电流无论工作频率还是幅值均有明显增大，进一步说明其发挥了“削峰填谷”的作用。

图6(g)为蓄电池SOC变化情况，前200 s小波功率分解策略优势不明显，原因在于初始阶段电机需求功率中低频成分较多，蓄电池放电功率较大，但200 s之后小波功率分解策略下蓄电池SOC变化曲线下降平缓，终止时刻SOC值为0.65，优于逻辑门限值功率分流策略的终止值0.62。对比说明采用小波功率分流策略后，由于适当增加了低频的充电功率，蓄电池SOC下降变缓，从而减少了蓄电池充放电循环次数。

4 结论

本文建立了混合动力汽车复合电源系统，提出了基于小波变换的功率分流控制策略，利用Matlab/ADVISOR仿真环境进行了开发和建模，在中国典型城市循环工况下进行仿真验证，得到如下结论：

1)复合电源系统中超级电容承担了驱动电机所需的瞬时功率和峰值功率，在保证复合电源系统功率需求的同时，发挥了“削峰填谷”的作用，使得蓄电池充放电过程更加平缓，有力地保护了蓄电池，发挥了复合电源系统优势；

2)设计的基于小波变换的功率分流控制策略，能够实现蓄电池和超级电容功率的合理分配，控制效果良好；

3)仿真结果验证了本文提出的复合电源功率分流控制策略的有效性，在指定工况下，能够满足整车行驶驱动需求。