2021年以色列秋令营一道不等式试题的探究
2022-11-25邓学忠
邓学忠
(山东省东营市第二中学 257000)
2021年以色列秋令营数学竞赛中有如下一道不等式试题:设a,b,c≥0,a+bc=2,求证:

不等式①的左边含有三个变量,右边只含有一个变量,两边极不对称.对此可考虑将左边第一项移到右边,使相同的变量在同一边,由此可以打开解题思路.
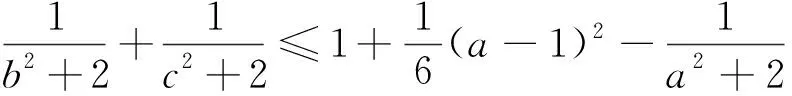


由已知易知0≤a≤2,由此可知不等式③成立,从而不等式①成立.
点评对不等式②的处理,按照减元策略,容易想到从左边入手,通过“先通分,再变形,后放缩”的方法,使左边含有两个变量的式子放缩为只含有一个与右边相同变量的式子,从而将三元不等式转化为一元不等式,实现了问题的根本性转变.
将上述赛题推广,可得到
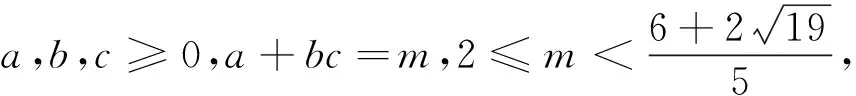


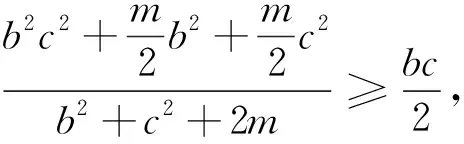


当我们将目光再次聚焦到不等式①,考虑将左边各个分母去平方项后进行放缩,并与右边加以比较,就会产生如下新的问题.
问题1设a,b,c>0,a+bc=2,求证:


由已知条件易知0≤a≤2,由此可知不等式⑧成立,从而不等式⑦成立.

考虑到不等式①的下界问题,经过探究得到:
问题2设a≥1,b,c≥0,a2+b2+c2=3,求证:


由已知条件易知1≤a2≤3,由此可知不等式成立,从而不等式⑨成立.
点评不等式⑨看似复杂,但是根据已知条件,容易想到利用柯西不等式对左边后两项的和进行放缩,由此转化为一元不等式问题,再通过合理的去分母与分解因式,转化为不等式就水落石出了.
由赛题可知,在已知条件下,不等式①的左边小于等于1是不可能的,如果改变已知条件,这种结果会成立吗?由此得到:
问题3正实数a,b,c满足abc(a+b+c)≥3,求证:
证明去分母后,不等式等价于a2b2c2+a2b2+c2a2+b2c2≥4,等价于(ab+bc+ca)2+a2b2c2≥4+2abc(a+b+c).

由舒尔不等式可知,(ab+bc+ca)3+9a2b2c2≥4abc(a+b+c)(ab+bc+ca),所以不等式可转化为4abc(a+b+c)(ab+bc+ca)+3a2b2c2(ab+bc+ca)≥12(ab+bc+ca)+9a2b2c2.

点评与赛题比较,问题3的条件变复杂了,而要证明的不等式却变简单了,但是由于条件发生了改变,因此不能将不等式左边第二、三项的和进行放缩了,只能采用“笨办法”去分母转化为整式不等式,因为式是一个非齐次的不等式,转化为不等式后利用舒尔不等式则是一种较为有效的解决途径,否则思路会就此搁浅.
数学问题的探究,是一个知识和方法不断深化的过程.因为思考才有了新问题,因为动手做才有了解决问题的途径,所以我们在数学解题的过程中,要不忘思考的初心,方得做题的始终,才能切实提升数学素养和解题能力.
