基于响应面法的伸缩臂架构有限元分析与优化
2022-11-25朱子青贺磊杨先海齐大新
朱子青,贺磊,杨先海,齐大新
(1.山东理工大学 机械工程学院,山东 淄博 255049;2.中国铁路济南局集团有限公司, 山东 济南 250001)
目前,散装物料仍延用以前的人工或斗式装载机进行装卸作业,不仅效率低下而且装卸成本很高[1],随着对货场、仓库以及加工厂内散装物料装卸效率要求的不断提高[2-4],急需一种针对散装物料装卸的可移式装卸机。本文对可移式散装物料装卸机的伸缩臂架构进行结构创新设计,通过仿真结果分析架构存在的缺陷,通过响应面法对伸缩臂架构参数进行优化并验证参数优化后架构的合理性,以期使所设计的伸缩臂架构满足实际散装物料装卸作业的需求。
1 伸缩臂架构的参数化设计
1.1 伸缩臂架构设计要求与参数化建模
一般情况下,仓库等场地范围有限且较为复杂,所以伸缩臂需要具有前后伸缩和上下摆动运动的能力。由于大臂的可伸缩性,还要保证散装物料在运输过程中不会因为伸缩臂各节之间的内部落差导致物料卡顿的情况出现,使物料可以从上料端顺利地传送到卸料端;同时,还要考虑各节伸缩臂之间的配合关系,保证伸缩臂在伸出和收缩过程中不会发生干涉。因此,散装物料伸缩臂架构的数据参数和设计要求如下:(1)伸缩臂架构收缩状态的长度为LS,与一节臂长度L1等同,伸缩臂完全伸长状态的长度为LE;(2)二节臂和三节臂的臂长分别为L2、L3;(3)伸缩臂一节臂高度为H1,二节臂高度为H2,三节臂高度为H3;(4)伸缩臂一节臂内侧宽度为W1,二节臂内侧宽度为W2,三节臂内侧宽度为W3;(5)三节伸缩臂的厚度分别为T1、T2、T3。
各节伸缩臂的长度可通过货场及仓库实际需求进行计算后选取,高度可通过理论计算及三维建模调整后选取,厚度为已有袋装物料伸缩臂侧板厚度。各节伸缩臂内宽通过带宽和各伸缩臂装配关系进行选取,各参数选取见表1。
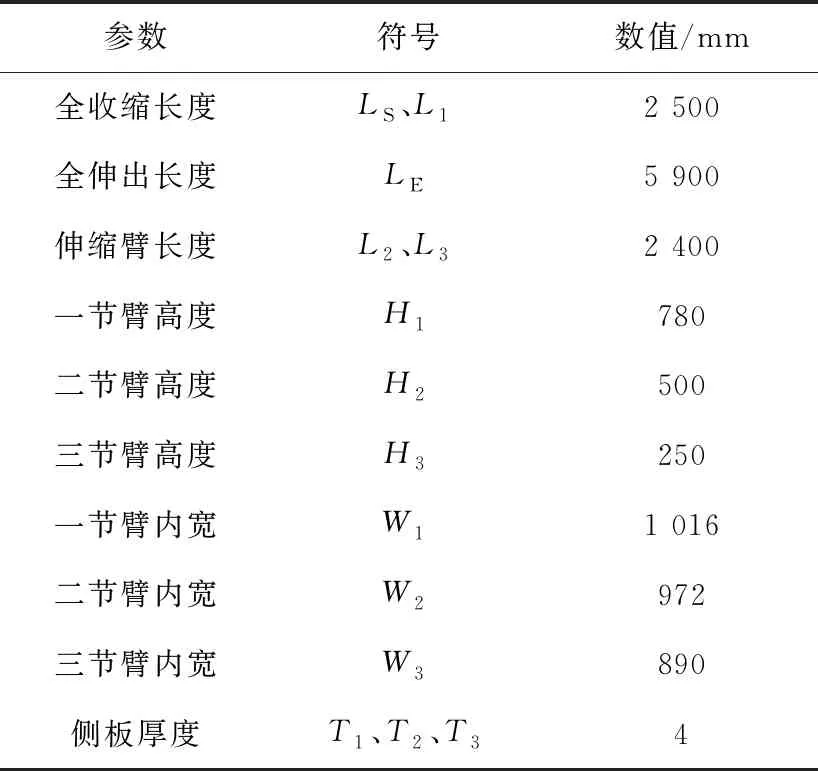
表1 伸缩臂结构参数
进行伸缩臂架构的建模时,需要建立与模型尺寸相对应的定位尺寸参数,在参数需要改变时,只需要改变主要的基本参数,其余尺寸均可根据基本尺寸进行自动改变,从而减少参数化建模的复杂程度。使用三维建模软件对三节伸缩臂架构进行三维参数化建模。
1.2 装配体的参数化建模
根据所设定的参数,将三节伸缩臂的三维模型导入三维建模软件的装配设计模块中进行装配操作。三维装配模型如图1所示。

1.一节臂;2.二节臂;3.三节臂;4.伸缩液压缸支撑梁;5.液压缸支撑梁;6.旋转法兰盘。
2 伸缩臂架构有限元分析
2.1 有限元模型简化与接触设置
装配体建模完成后,需要对其进行有限元仿真分析,针对其变形、受力进行分析计算,并校核其结构的变形和受力情况。
先将所建三维装配体模型中对受力影响较小的结构进行简化,结构简化原则如下:(1)不考虑钢板焊接应力及焊缝的影响;(2)去除伸缩臂上为安装其他零件所设置的孔洞;(3)将主要受力部件进行切割处理,方便网格划分;(4)将部分焊组件及非主要分析部件简化为单实体零件装配[3-7]。将简化后的三维模型导入有限元分析软件中,伸缩臂侧板及支撑横梁的材料均设置为Q235,滑轨、滑块及滑轨加强筋的材料均设置为45号钢,滑块与滑轨之间连接接触的耐磨块材料设置为尼龙,各材料参数见表2。
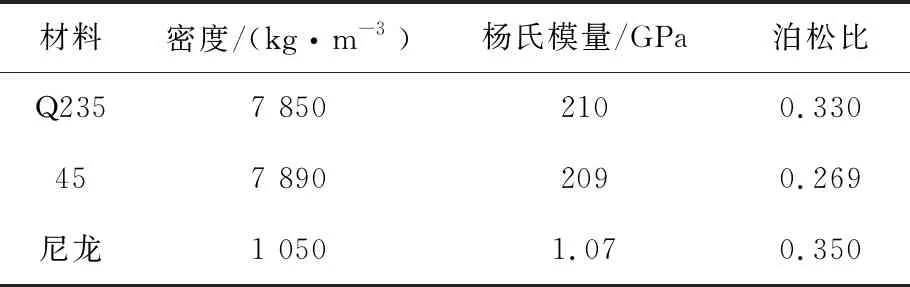
表2 材料参数
2.2 网格划分及边界设置
简化后的有限元模型需要进行网格划分,为后续的受力和变形分析做好准备。通过面网格尺寸设置,保证所有面的网格数保持在两层及以上[8]。主要部件网格划分如图2所示,整体网格划分如图3所示。

图2 横撑及滑轨滑块网格划分

图3 伸缩臂整体网格划分
在伸缩臂上下摆动运动中,通过两个对称分布的转动法兰盘以及升降液压缸进行支撑和定位,因此对液压缸与液压缸支撑梁销接处进行圆柱固定设置,对转动法兰盘的转轴进行固定设置。
2.3 载荷计算与载荷施加
散装物料伸缩臂运输的货物主要为矿石,当满载物料时,物料的重力通过传送带作用于三节伸缩臂横撑上的托辊,所以需要对散装物料作用于皮带托辊上的力进行理论计算。
本文应用朗肯(Rankine)理论计算物料所受侧向压强从而计算托辊受力[9],常见的槽型物料堆积截面形状如图4所示。

图4 物料堆积截面图
整个截面横截面积S为
(B′-2c-w)cosλ]2tanρ,
(1)
式中:S1为梯形BCDE的截面面积;S2为顶部物料BEG截面面积;B′为带宽;c为空边距,c=0.05B′+0.025 m;λ为槽型托辊组槽角;ρ为物料堆积角;w为中间输送带宽度。
中间托辊承载物料的横截面积S3为
(2)
式中:S4为长方形MCDN区域的面积;S5为MNG抛物线区域面积。
由式(1)和式(2)可求出中间托辊承载的物料占所有物料的比例m为
(3)
在实际计算中提出一个新的压强系数Ku来表示整个皮带的侧向合压强系数,在一个托辊间距内,可以认为处于主动状态的物料和处于被动状态的物料均为二分之一,所以
(4)
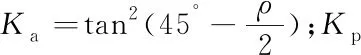
通过上述分析,可求出托辊连接处物料的高H,即为图4中DN的长度,
(B′-2c-w)cosλ]tanρ-
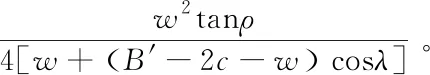
(5)
由朗肯土压力理论可知,当输送机倾角为0°时,侧托辊所受侧推力Fs为
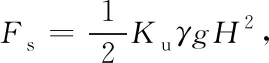
(6)
式中:Ku为侧向合压强系数;γ为物料堆积密度;g为重力加速度,取g=9.8 m/s2。
中间托辊受力为
Fm=(K1qG+K2qB)ag,
(7)
式中:a为托辊间距;K1为物料系数,取K1=0.7;K2为输送带系数,取K2=0.4;qG为单位长度物料的质量;qB为单位长度输送带的质量[10]。
本文选用磁铁矿作为物料模拟托辊所受压应力,磁铁矿及托辊组参数见表3。
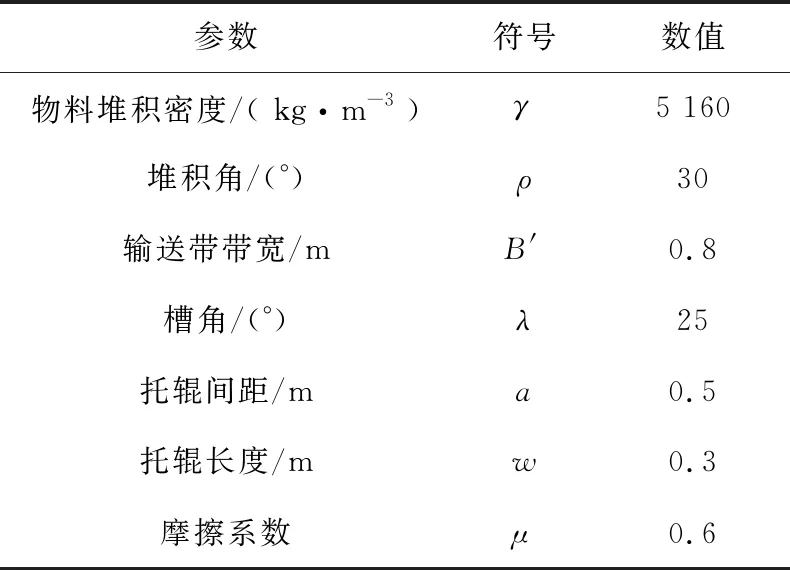
表3 磁铁矿及托辊组各项参数
计算得侧边法向力为295 N,中间法向力为792 N。将步数设置为10步,增加重力加速度,然后从伸出端横撑开始每步施加一根横撑上的受力,将所受应力进行换算施加到三节伸缩臂的各个横撑后进行仿真分析。
2.4 伸缩臂的刚度计算
为保证伸缩臂工作时的安全性,应控制伸缩臂架构伸出端的最大挠度f。
运用叠加法进行挠度计算,整个伸缩臂可以近似看作承受均布载荷q的伸出简支梁,其结构如图5所示。在B点进行分节,分别计算CB段和AB段在均布载荷q下的挠度,即
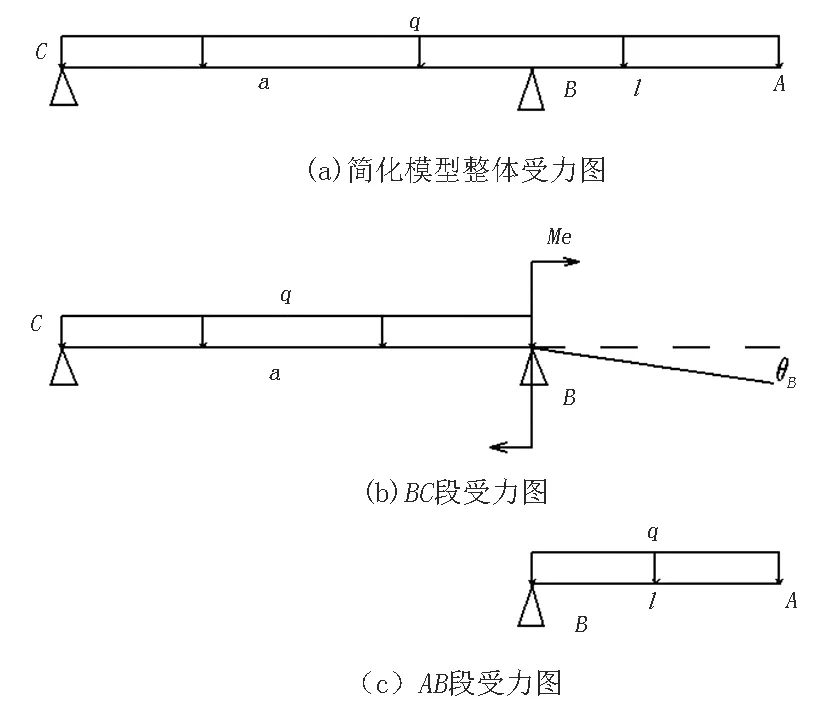
图5 简化模型
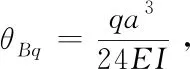
(8)
(9)
(10)
(11)
总挠度为
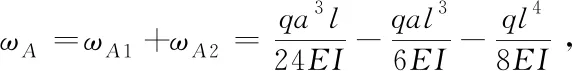
(12)
式中:θBq为BC段在均布载荷q的作用下B点处的旋转角;θBMe为BC段在弯矩Me作用下B点处的旋转角;ωA1为BC段在受力作用下使A端产生的挠度;ωA2为AB段在均布载荷作用下A端产生的挠度;ωA为A点最大的挠度;E为材料弹性模量,取E=210 GPa;I为惯性矩。
将各参数代入式(12)中可得伸缩臂最大挠度为8.2 mm。伸缩臂允许挠度[11]为12.25 mm,由此说明理论上伸缩臂架刚度方面满足要求。
2.5 静力学仿真结果及分析
根据上述步骤进行仿真后的变形结果如图6所示,受力结果如图7所示。由图6可知,当载荷施加完成后,整个伸缩臂的最大变形量为10.763 mm,最大变形出现位置为伸出端最前端, 与理论计算值相差不大,略小于伸出端允许挠度,伸缩臂刚度满足要求;由图7可知,伸缩臂所受最大应力为256.26 MPa,最大应力出现在滑轨支撑块上,其材料为45号钢,屈服强度为355 MPa,满足实际要求。所以,仿真结果满足所需的变形和受力情况。
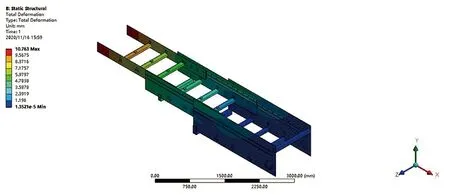
图6 仿真变形结果
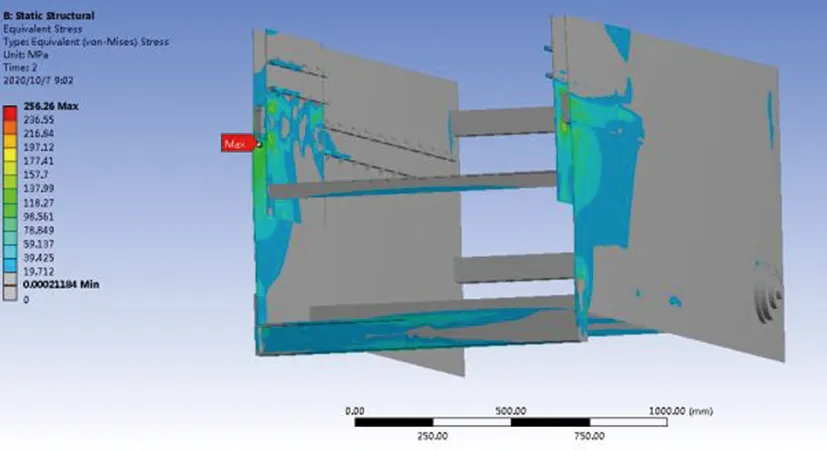
图7 仿真受力结果
2.6 模态分析
模态分析是用于提取结构固有频率和振型的一种有限元分析,可以为结构修改提供重要的理论依据,进行模态分析可以避免结构产生共振,同时也为进行动力学分析打下基础。以伸缩臂静力学结果为约束进行6阶的模态分析,模态分析结果如图8所示,所得分析结果见表4。从模态分析的各阶振型和变形情况可以看出,对伸缩臂工作时影响较大的前3阶振动变形最大振幅点大多发生在伸缩臂伸出端,因此对伸缩臂伸出端进行尺寸优化从而提高其横向刚度是很有必要的。
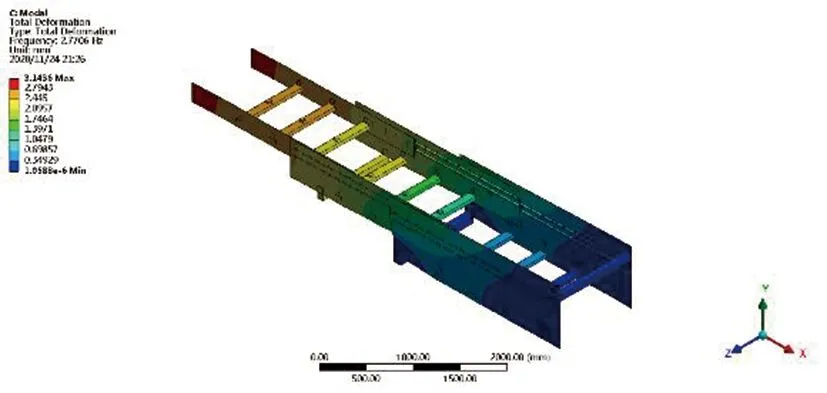
(a)第1阶模态振型

表4 约束模态下前6阶模态计算结果
3 伸缩臂响应面法多目标优化
采用有限元分析软件中的目标驱动优化模块对伸缩臂架构尺寸进行优化。Design Explorer通过实验设计和响应曲面技术来描述设计变量和优化目标之间的关系,通过实验设计法产生多种数据,再用设计变量的参数来研究设计变量对优化目标的影响,通过有限个设计点拟合成响应曲面(线)进行研究,最终可以得到一个较优化的值。
选取三节臂的侧板长度L3、厚度T3和高度H3作为设计变量,以伸缩臂静力学最大变形量δ≤12.25 mm作为约束条件,以静力学最大变形量δ、前3阶模态分析最大变形量δ1、δ2、δ3以及伸缩臂总体质量m最小为优化目标进行优化,建立的优化数学模型为
(13)
3.1 响应面法理论
响应面法就是采用一种数学的方法,通过一个近似的表达式来表达出所需要的功能函数,功能函数是采用一定的数据通过线性或二次多项式的形式拟合,得到一个性能值与各数据的响应函数[12]。在实际计算过程中经常会用到数学中的多次线性插值,插值函数为
(14)
式中:Ln(x)为变量x的函数;li(x)为x的基函数;yi为系数。
首先用多种数据计算得到插值函数,然后在设计变量x的约束下,得到最优的输出变量,即较优响应结果。
3.2 响应面优化
从上述分析中可知,伸缩臂可以满足设计方面的要求,但同时可以在横向刚度方面进行优化,使其具有更好的性能。在有限元分析软件中选择响应面优化工具,将前述伸缩臂的参数作为输入量并定义其范围,以静力学最大变形、目标质量以及前3阶模态最大变形为优化目标,将优化目标的约束条件均设置为最小值,最大变形的数值约束为小于12.25 mm,建立与三节臂长度、厚度、高度3个尺寸相对应的响应函数并进行优化,得到3组候选数据(见表5)。以模态分析中变形最小为最先优化目标,选择第1组数据为优化结果,对参数进行近似取整导入模型计算并对优化前后的参数进行对比,对比结果见表6。

表5 候选点数据

表6 优化前后结果对比
3.3 优化后静力学受力仿真分析
优化完成后,通过参数修改进行模型更新并调整装配尺寸,对模型进行静力学仿真,验证优化后结构的变形和受力情况是否满足设计要求,其理论计算和仿真步骤与前文相同,仿真结果如图9和图10所示。优化后最大变形为11.023 mm,低于许用挠度[11]11.46 mm,满足刚度要求;最大应力为181.34 MPa,最大应力位于二节臂滑块与侧板之间的固定板上,该零件材料为Q235,最大屈服强度为235 MPa,满足材料强度。所以优化后尺寸满足设计要求。

图9 优化后变形云图

图10 优化后应力云图
4 结束语
本文基于三维建模软件和有限元仿真分析软件,对散装物料上料伸缩臂进行了有限元仿真和参数优化。
1)完成了散装物料上料伸缩臂的结构设计,并对其进行静力学和模态仿真分析,所得结果满足设计要求。
2)在整体结构满足实际要求的条件下,通过对仿真结构的模态分析,得出结构存在的不足以及改进的方向,确定优化参数,运用响应面法对结果进行多目标优化,最终获得优化后的参数。
3)以伸出端最大变形以及模态分析前3阶最大变形作为最先优化目标,优化后模态分析前3阶最大变形最分别减少9.28%、46.61%、98%,结构质量减少22.79%,在满足横向刚度优化目标的同时减少了伸缩臂整体质量,且优化后伸缩臂架构的变形与受力均满足设计要求。
