非凸最优化问题可行解序列的有限终止性

张猛，赵文玲，郭希敏，张茜

(山东理工大学 数学与统计学院, 山东 淄博 255049)

设x∈Rn，〈·，·〉表示Rn中的内积。

x在闭集C上的投影定义为

x到C的距离定义为

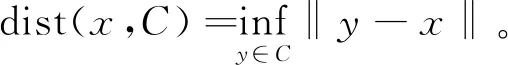
如果C是闭集, 则有

dist(x,C)=‖PC(x)-x‖。

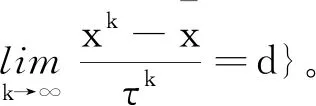
C的极锥定义为

C°={y∈Rn|〈y,x〉≤0,∀x∈C}。

据文献[1]命题6.5,本文有

TC(x)°=NC(x)。

当C是凸集时,由文献[1]定理6.9, 本文有

∀x∈C}。

若∇Sf(x)=PTS(x)(-∇f(x))，称之为f(·)在S上的投影梯度, 简记作 ∇Sf。

序列{xk}⊂Rn有限终止于C, 如果存在k0,当k≥k0时，有xk∈C。

1 强非退化集与弱强极小集

考虑最优化问题(NP):

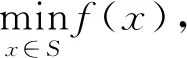
当f(x)是凸函数时, (NP)是凸最优化问题；当f(x)是非凸函数时, (NP)是非凸最优化问题；当f(x)的梯度∇f连续时, (NP)是光滑最优化问题。

对于最优化问题(NP)的解集S*, Burke等[2]将强单一极小点的概念进行推广, 建立了弱强极小(weak sharp minima)集的概念, 它包含了解集是非单点集的情况。 如果存在仅依赖于f,S和S*的常数α*>0, 使得对∀x∈S与∀x*∈S有

f(x)-f(x*)≥α*dist(x,S*)，

(1)

本文称S*是弱强极小集,

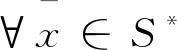
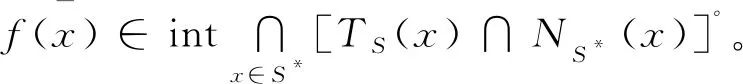
(2)

关于最优化问题由算法所产生的可行解序列的有限终止性问题,长期受到广泛的关注与研究。解集强非退化性的概念在可行解序列有限终止性问题中也起到了重要的作用[5-8]。 目前已验证最优化问题在解集满足弱强极小或(强)非退化的条件下能使某些逼近点算法[9-12]与其他类型算法[13-18]的可行解序列具有有限终止性。

对于凸最优化问题(NP)解集的强非退化集与弱强极小集的概念,文献[6，8]给出了如下定义。

定义1如果

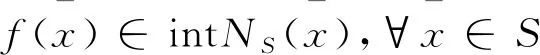
(3)

定义2如果

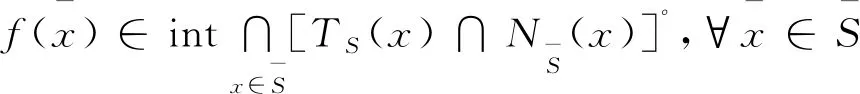
(4)

Burke等[2]关于凸最优化问题的可行解序列的有限终止性定理(简化形式)如下。

定理1对非凸最优化问题是不成立的。举例如下。

例1非凸最优化问题

s.t. 1-x≤0。

其最优解集为

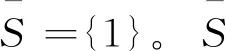
是弱强极小集也是非退化集。对于可行解序列{xk}={2,3,…,k,…}, 有(注意TS(xk)=R)

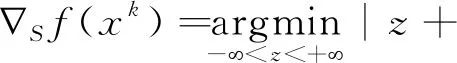
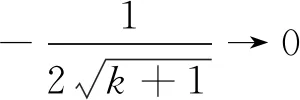
由此例知, 对非凸最优化问题, 虽然它的解集既是弱强极小集又是强非退化集, 但定理1结论并不成立。 因此本文有必要对非凸最优化问题解集的强非退化与弱强极小的概念进行推广,进一步研究非凸最优化问题可行解序列有限终止性的条件。

本文首先对非凸最优化问题(NP)的解集, 给出广义强非退化集和广义弱强极小集的概念,它们分别是凸最优化问题中强非退化集与弱强极小集概念的推广。 然后在非凸最优化问题(NP)的解集是广义强非退化或广义弱强极小的情况下, 分别给出了其可行解序列有限终止于解集的充分与必要条件， 这些结果分别包含了现有相关文献([2,14,17,19]) 中相应的结论。 最后讨论了广义强非退化和广义弱强极小的简单应用。

2 广义强非退化集与广义弱强极小集

为了进一步研究非凸最优化问题可行解序列的有限终止性的条件,给出广义强非退化集与广义弱强极小集的定义。

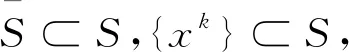
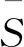
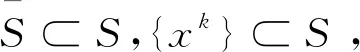
xk-PS(xk)〉≥0。

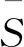
下面举例说明, 解集的广义强非退化与广义弱强极小分别是强非退化与弱强极小的推广。

例2对最优化问题

是广义强非退化集也是广义弱强极小集。

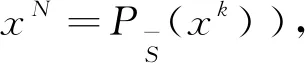
并且

相反地，本文有下面的命题。

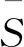
例2与命题1说明了广义强非退化集与广义弱强极小集是凸最优化问题解集的强非退化集与弱强极小集的实际性推广。

(5)

因此有

(6)

由式(3)与式(6)知存在常数α>0使得

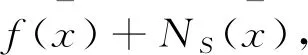
所以

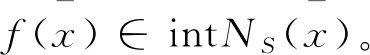
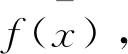
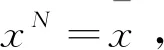
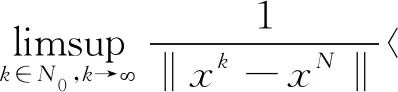
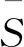
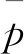
由上式即得

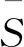
3 有限终止性条件

定理2设在非凸最优化问题(NP)中,

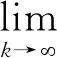
(7)

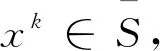
因为S为闭凸集, 所以对∀k∈K有

(8)

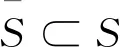
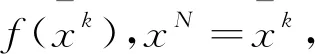
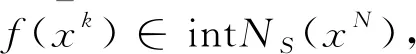
则∃α>0使得

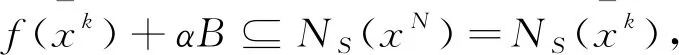
(9)

式中B为Rn中的单位球。 由式(8)与式 (9)可推出

由命题2与定理2即得下面推论。

注1推论1即是文献[17]的定理5.3，后者是文献[14] 推论3.5的推广。

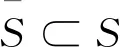
(10)

证明必要性显然成立, 下面证明充分性。

(11)

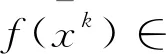
(12)

由式(12)可知, ∃α>0使得对所有充分大的k∈K有

(13)

式中B为Rn中的单位球。 由式(11)与式(13)可推出

这与式(10)矛盾, 所以定理3成立。

由命题1与定理3即得下面推论。

注2推论2即是文献[19]的定理3.1， 后者推广并改进了文献[2]的定理4.7。

由命题3与定理3即得下面推论。

4 应用

本节研究广义强非退化集与广义弱强极小集的应用。

定理4设在最优化问题(NP)中, {xk}⊂S,yk=PS(xk-∇

(14)

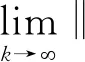
(15)

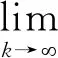
由投影性质, 对∀y∈S有

〈xk-∇f(xk)-yk,y-yk〉≤0,

即

〈∇f(yk),y-yk〉≤〈yk-xk,y-yk〉+

〈∇f(xk)-∇f(yk),y-yk〉。

(16)

对∀d∈TS(yk),‖d‖≤1, 由切锥的定义与式(16)得

由文献[20]的引理3.1得

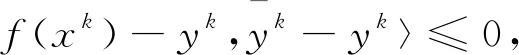
(17)

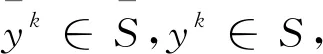
(18)

将式(16)与式(17)相加得

因此有

由已知条件,根据上式可得

再由三角不等式有

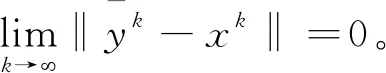
再根据∇f(·)在{xk}的一个δ邻域B({xk},δ)上一致连续性,可知{xk}满足定理4的条件, 因此得证。

注3在凸最优化问题(NP)中, 强非退化集的概念是弱强极小集的特例,所以推论4对于凸优化问题(NP)也成立, 因此,由推论4可以得到文献[2]中定理4.7的充分条件。

定理5设在非凸最优化问题(NP)中, {xk}⊂S,yk=PS(xk-∇

将定理5应用到凸最优化问题,可以得到下面推论。

此推论可以用类似于推论4的方法证明。

注4推论5是文献[2]中定理4.7可行解序列有限终止性的充分条件。

5 结束语

解集的强非退化或弱强极小性是逼近点算法以及许多最优化算法具有有限终止性的充分条件, 但在许多情况下, 最优化问题解集的强非退化和弱强极小性并不成立。 为了弥补这种缺陷, 本文给出了最优化问题中广义强非退化集和广义弱强极小集的概念, 这为最优化问题的可行解序列有限终止性提供了比强非退化和弱强极小性更弱的充分条件。