珠三角典型软土硬化土模型及其工程应用研究

2022-11-25王祥秋杨柱郑土永

山东理工大学学报（自然科学版） 2022年1期

王祥秋，杨柱，郑土永

(1.佛山科学技术学院交通与土木建筑学院，广东佛山 528000;2.北京市市政工程设计研究总院，北京 100037)

目前，有限元计算方法在岩土工程中得到了广泛的应用，而本构模型的选取及模型参数的确定是进行数值计算的关键。宋二祥等[1]，王海波等[2]、王卫东等[3-4]将硬化土本构模型应用于深基坑工程开挖数值模拟；庞小朝等[5]、杨兰强等[6]通过室内试验获得了岩土体硬化土本构模型参数，分析了硬化土本构模型的可行性； Sukkarak等[7]利用硬化土本构模型分析了大坝地基沉降规律；温科伟等[8]、沈玺[9]基于硬化土本构模型对地铁隧道的变形特性进行分析；谢东武等[10]通过室内三轴试验确定了上海软土小应变硬化土模型参数，并基于土单元数值模拟对模型参数的敏感性进行分析。研究结果表明，硬化土弹塑性本构模型能综合考虑黏性土的剪胀性和中性加载，能区分加荷和卸荷特性，对复杂环境下岩土与地下工程开挖数值分析具有很好的适用性。而目前内嵌硬化土本构模型(HS模型)的岩土分析软件只有Midas GTS、Plaxis和Zsoil等，其它岩土分析软件如FLAC3D、ABAQUS等有限元分析平台尚未内嵌硬化土本构模型，在一定程度上影响了相关软件在岩土工程领域的广泛使用。为此，国内外学者针对相关软件开展了HS模型的二次开发研究，如姜兆华等[11]、王春波等[12]基于VC++编程环境，利用FLAC3D提供的二次开发平台编制HS模型的有限差分程序，实现了HS模型在FLAC3D的二次开发，满足了岩土工程领域大变形问题计算的需要。而ABAQUS作为具有强大非线性问题求解功能的有限元分析软件，目前尚未实现硬化土模型内嵌功能，开发研制基于ABAQUS平台的HS模型分析功能则可满足岩土工程领域非线性小变形问题计算的需要。

为此,本文基于ABAQUS软件强大的自定义材料模型开发功能，通过推导硬化土本构关键算法，基于Fortran编程环境，利用ABAQUS提供的用户材料UMAT子程序接口，实现HS本构模型的二次开发。利用GDS多功能应力路径三轴仪对原状土进行固结排水剪切实验、三轴固结排水加载-卸载-再加载实验以及三联固结实验测定珠三角地区典型软土HS模型参数，并通过实验数据与数值计算结果对比分析及深基坑工程实例监测结果与模拟结果比较，验证HS本构模型UMAT子程序的合理性及可靠性。

1 硬化土本构模型

硬化本构模型(即HS模型)由Schanz等[13]在VERMEER双硬化模型基础上提出，该模型采用 Mohr-Coulomb破坏准则。土体弹性阶段采用双刚度分别考虑土体加载与卸载影响，并假定土体刚度与应力水平相关，竖向应变ε1与偏应力q之间满足双曲线关系[4-5]，即

(1)

其中

(2)

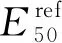
假定土体塑性阶段屈服面由剪切屈服面和压缩屈服面两部分组成。剪切屈服面(剪切屈服函数Fs)定义为

(3)

(4)

其中

(5)

若采用关联流动法则,则剪切屈服面塑性势函数可表示为

(6)

(7)

式中：ψm为机动剪胀角；φm为机动摩擦角；φcv为临界摩擦角；ψ为土体固有剪胀角。

压缩屈服面(压缩屈服函数Fv)定义为

(8)

其中

(9)

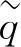
(10)

若采用关联流动法则,则压缩屈服面塑性势函数可表示为

(11)

2 二次开发关键算法

基于ABAQUS软件的二次开发中最关键的问题是如何选择本构模型的积分算法。常用的积分算法主要包括隐式积分算法和显式积分算法，其中，显式积分算法又包括基本刚度法、中点刚度法以及SLOAN提出的带误差控制的修正向后EULER返回算法。本文主要采用基本刚度法对硬化土本构模型进行二次开发，其基本步骤如下：

1)计算弹性预测应力。在第n步应力{σn}已知的情况下，先按虎克定律预测第n+1步的试探应力{σn+1,trial}。

{σn+1,trial}={σn}+De{Δεn+1}，

(12)

式中：De为弹性刚度矩阵；{Δεn+1}为应变增量矩阵。

2)屈服准则判断。将试探应力{σn+1,trial}分别代入式(3)和式(8)。如果Fv({σn+1,trial}，{kv})<0，Fs({σn+1,trial}，{ks})<0,则表明材料此时处于弹性阶段，硬化参数{kv}和{ks}保持不变，刚度矩阵为弹性刚度矩阵De，上述试探应力即为第n+1个增量步的应力；如果Fv({σn+1,trial}，{kv})≥0或Fs({σn+1,trial}，{ks})≥0,则表明材料处于单屈服阶段，可能发生剪切屈服或者压缩屈服，此时应力增量按式(13)确定，刚度矩阵按式(14)确定；如果Fv({σn+1,trial}，{kv})≥0且Fs({σn+1,trial}，{ks})≥0,则表明材料同时发生剪切屈服和压缩屈服，此时应力增量按式(13)确定，刚度矩阵按式(29)确定。

3)求解增量本构方程对应的弹塑性矩阵及应力增量。根据塑性理论，则有弹塑性本构关系的增量本构方程的一般形式为

{Δσn+1}=Dep{Δεn+1}，

(13)

式中Dep为弹塑性刚度矩阵。

对于只发生剪切屈服或者压缩屈服，则有增量本构关系的弹塑性刚度矩阵为

(14)

对于双屈服面模型刚度矩阵，部分做法是先计算柔度矩阵，再通过求逆得到刚度矩阵，但是求逆往往需要耗费大量计算时间[14]。本文采用David等[15]人的方法，直接推导双屈服面模型弹塑性刚度矩阵,这种方法同样可以适用于三屈服面模型。

当同时发生剪切屈服以及压缩屈服时，则总应变增量主要由弹性应变增量{Δεe}、剪切应变增量{Δεps}以及压缩应变增量{Δεpv}组成，即

{Δε}={Δεe}+{Δεps}+{Δεpv}，

(15)

而根据弹塑性理论，总应力增量可以表示为

{Δσ}=De{Δεe}

(16)

或者

{Δεe}=De-1{Δσ}。

(17)

将式(15)代入式(16)可得

{Δσ}=De({Δε}-{Δεps}-{Δεpv})，

(18)

其中，剪切塑性应变和压缩塑性应变分别与剪切屈服函数及压缩屈服函数对应的塑性势函数相关，且

(19)

式中：λs和λv为塑性比例因子。

将式(19)代入式(18)则有

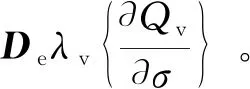
(20)

又由一致性条件得

(21)

将式(20)代入式(21)得

{

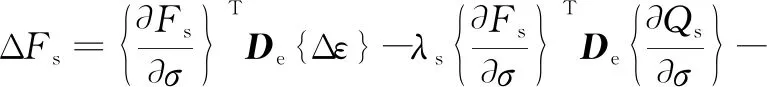
(22)

其中

(23)

式(22)也可改写为

(24)

其中：

(25)

(26)

(27)

联立式(24)解得

(28)

代入式(20)得

(29)

其中：

Ω=LssLvv-LsvLvs，

(30)

(31)

(32)

4)对屈服函数和势函数求一阶导数。为了便于数值计算，根据弹塑性理论，将硬化土本构模型的屈服函数和势函数表示为应力不变量的形式，其中：I1为第一应力不变量；J2为第二偏应力不变量；J3为第三偏应力不变量；θ为应力洛德角。则剪切屈服函数可以表达为

(33)

压缩屈服函数可以表达为

Fv=

(34)

与剪切屈服函数相对应的塑性势函数为

(35)

屈服函数流动矢量可以表示为

(36)

式中

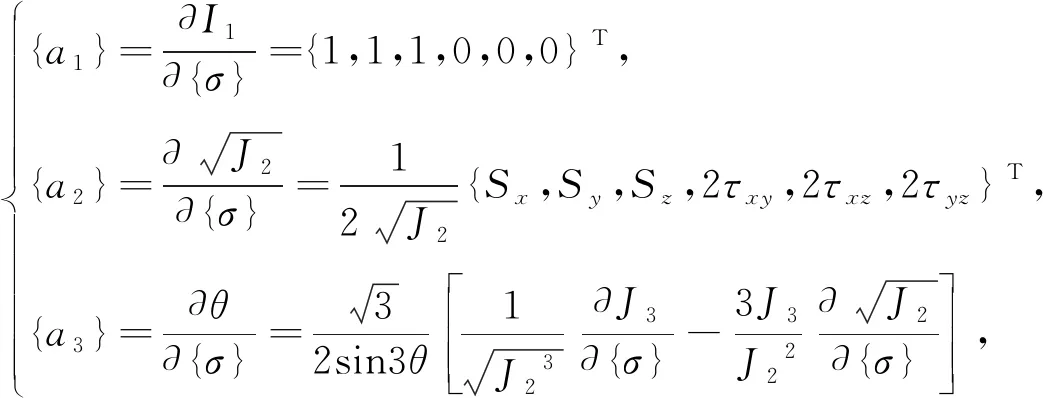
(37)

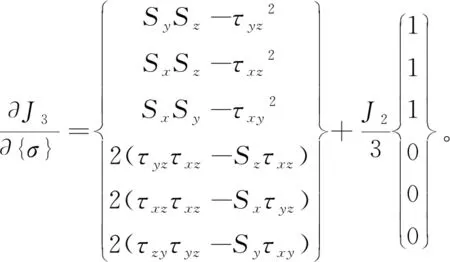
对于剪切屈服函数，式(36)中参量C1、C2、C3按下式计算：

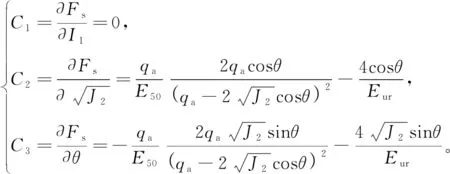
(38)

对于压缩屈服函数，式(36)中参量C1、C2、C3则按下式计算：

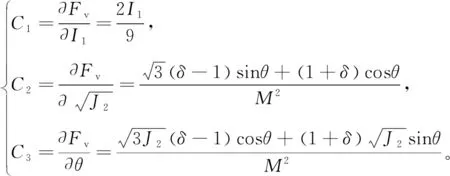
(39)

与屈服函数流动矢量计算过程一样，塑性势函数流动矢量的表达式如下：

D1{a1}+D2{a2}+D3{a3}。

(40)

对于剪切屈服函数对应的塑性势函数，式中参量D1、D2、D3按下式计算：

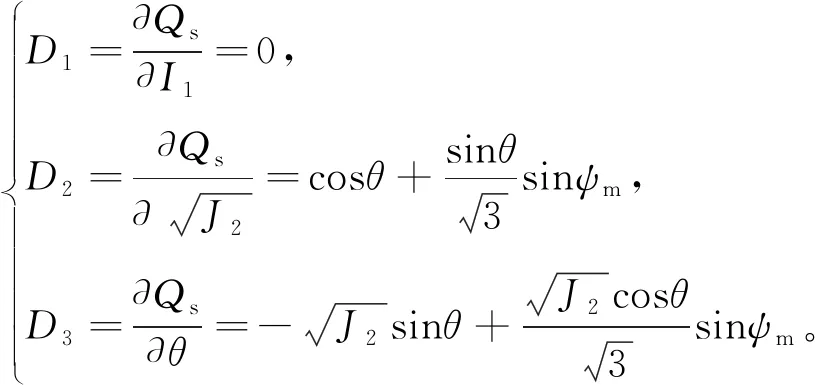
(41)

5)更新应力、应变和硬化参数。

{σn+1}={σn}+{Δσn+1}。

(42)

当同时发生剪切应变和压缩应变时，第n+1步结束时应变更新为

(43)

当仅发生剪切应变或压缩应变时，第n+1步结束时应变更新为

(44)

或者

(45)

剪切屈服硬化参数增量为

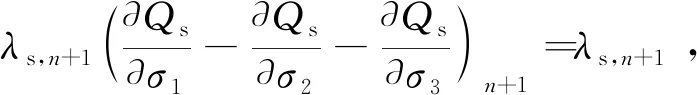
(46)

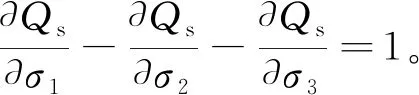
第n+1步结束时，剪切屈服硬化参量更新为

(47)

对于压缩屈服，塑性体应变增量为

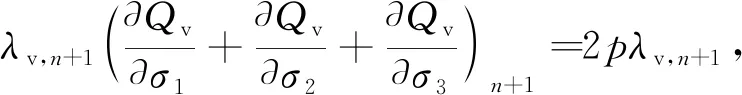
(48)

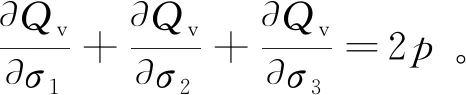
压缩屈服硬化参数增量为

(49)

第n+1步结束时压缩屈服硬化参量更新为

pc,n+1=pc,n+Δpc,n+1=

(50)

3 子程序开发关键技术

根据上述硬化土本构模型关键算法，基于ABAQUS提供的UMAT子程序接口,利用Fortran编程语言环境可开发HS模型的UMAT子程序。子程序开发中应注意如下关键技术问题:

1)子程序编写应符合HS模型和弹塑性有限元计算特点，同时其输入输出格式及变量名应注意与标准ABAQUS程序一致。

2)ABAQUS分析软件中，应力应变符号以拉为正、压为负，主应力、主应变排序与岩土力学有关规定相反。

3)程序编写过程可以输入write(7，*),从而可在保存于文件夹内的msg文件中输出所关心的变量并加以考察。

4)UMAT开始计算时，应避免ABAQUS主程序传入初始应力为零而导致计算过程出现极大值现象。

UMAT子程序调用与求解流程如图1所示。

图1 UMAT子程序开发与工作流程图

1)在ABAQUS程序求解时，每一个增量加载步开始时，ABAQUS主程序都会在单元积分点上调用UMAT子程序，传入当前状态的总应力、应变增量和用户自定义状态变量等基本信息，同时传入主程序计算得出的应变增量。

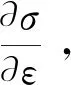
3)变量更新值通过接口返回主程序，雅可比矩阵将同单元应变矩阵运算形成单元刚度矩阵，进而获得总体刚度矩阵；主程序根据当前荷载增量求解位移增量并进行平衡校核；如果不满足用户指定的误差或者缺省值，ABAQUS将进行迭代，直到满足收敛条件为止，然后进行下一增量步的求解。

4 工程实例

4.1 工程概况

珠三角某地铁车站采用地下三层岛式结构，基坑全长211.4 m，标准段宽20.9 m，车站基坑开挖深度为24.22～26.72 m，采用1 000 mm厚的地下连续墙作为围护结构，地连墙嵌固深度为6 m。考虑到车站周边环境条件复杂，车站深基坑工程采用明挖法施工，与地铁1号线换乘节点处采用暗挖法施工。基坑边线西北侧距离某广场地下室边线仅2.48 m。自上而下设四道支撑和角撑，分别位于-1.7 m、-7.3 m、-14.1 m、-19.8 m和-24.2 m。竖向标准段第一道和第三道采用砼支撑，第二道和第四道采用φ609钢支撑，并分别施加400 kN和600 kN预应力，换乘节点段和端头井采用四道砼支撑，基坑支护结构平面布置如图2所示。

图2 车站基坑支护结构平面图

4.2 三维有限元分析模型

采用ABAQUS大型有限元分析软件对车站深基坑工程力学特性进行分析。为消除边界效应影响，根据实际基坑的开挖深度及平面尺寸建立的模型空间尺寸为350 m×200 m×60 m(长×宽×高)。土体采用实体8节点减缩单元模拟，单元类型为C3D8R。车站结构及连续墙变形均采用实体8节点协调单元模拟，单元类型为C3D8I；砼支撑、钢支撑及立柱采用梁单元(Beam)，单元类型为B31，计算模型如图3所示。地连墙与土体的作用、车站结构与土体的作用及地连墙与车站结构的作用均选择tie连接，只传递拉力和压力且不产生相对位移。对模型整体施加重力荷载并限制模型侧向位移及底部竖向位移。

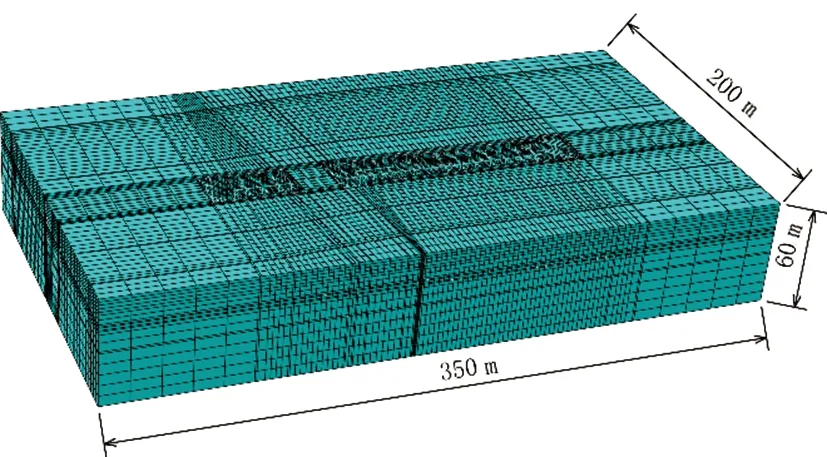
(a)基坑整体分析模型

4.3 计算参数

根据岩土工程勘察报告，利用GDS多功能应力路径三轴仪对原状土进行固结排水剪切实验、三轴固结排水加载-卸载-再加载试验以及利用三联固结仪进行常规固结实验测定各土层HS模型参数，具体参数见表1。

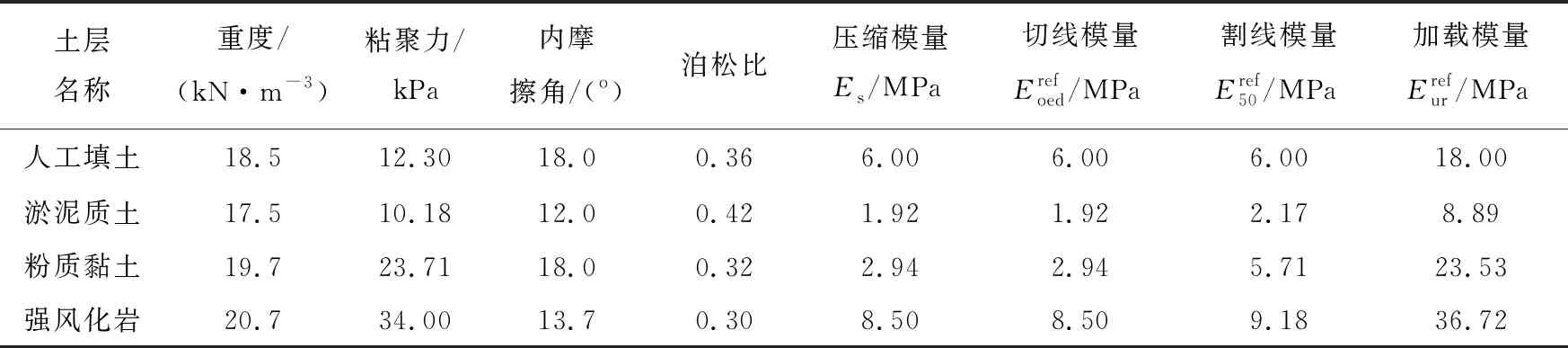
表1 车站深基坑土层主要物理力学性能参数

基坑支护结构(含地下连续墙、内支撑)采用线弹性模型进行模拟，地下连续墙、混凝土支撑均采用C35混凝土，考虑到施工因素影响，其弹性模量按80%折减取为24 GPa，泊松比取0.2；钢管支撑和钢围檩弹性模量取为210 GPa，泊松比为0.3。为了客观地模拟地铁车站深基坑施工开挖力学特性，根据深基坑支护结构设计方案以及实际开挖工况,结合车站换乘节点与3号线地铁车站深基坑开挖先后次序安排，确定有限元模拟的施工开挖步，计算工况见表2。

表2 计算工况

4.4 模拟结果与监测数据对比分析

为了对比分析基于HS模型的有限元数值结果与现场监测成果的吻合程度，任选基坑长边典型监测点ZQT4和ZQT14作为分析对象，如图4所示。

图4 车站基坑监测点平面图

由现场监测和有限元分析可得监测点ZQT4和ZQT14处地下连续墙深部位移在基坑关键施工步即第4施工步(开挖第一层土体)、第6施工步(开挖第三层土体)及第9施工步(开挖第六层土体)时的变化曲线(如图5所示)。

由图5可知，在车站深基坑开挖过程中，地下连续墙深部位移监测值与计算值的变形趋势基本吻合。在基坑开挖初期(第4步)，两者误差较小；随着基坑开挖深度不断增加，地下连续墙深部位移拐点以上部分的监测值与计算值仍然具有较高的吻合度，当基坑开挖到底时(第9步)，监测点ZQT4处地下连续墙深部位移监测最大值为24.5 mm,数值模拟深部位移最大值为22.3 mm；监测点ZQT14处地下连续墙深部位移监测最大值为23.8 mm,数值模拟深部位移最大值为21.4 mm，两者最大误差仅为11.2%。但在拐点以下部分，其监测值与有限元模拟值的误差逐渐增大，其原因可能与软土深基坑工程随着开挖深度不断增大，基坑开挖时空效应愈来愈明显，以及由于基坑施工过程未能及时施加钢支撑等因素有关。而基于MC模型得出的墙体深部位移计算值较HS模型以及现场监测值偏小，主要原因在于MC模型只定义了一个弹性模量，未能考虑土体加载和卸载模量的差异性，且无法考虑应力路径的影响，导致基坑开挖产生较大的坑底回弹，从而减小了墙体的变形。