基于改进三维形状上下文的点云配准

赵云涛，齐佳祥，李维刚，甘 镭

（1.武汉科技大学 冶金自动化与检测技术教育部工程研究中心，湖北 武汉 430081；2.武汉科技大学 信息科学与工程学院，湖北 武汉 430081）

1 引 言

3D视觉传感器日新月异，为视觉图像的理论研究以及点云数据的应用提供了无限可能，而配准作为视觉领域的核心，近些年对于配准的研究层出不穷。三维点云配准的目的是计算最优匹配，将不同视图中的点集转换到全局坐标下。三维点云配准主要分为两阶段：初始配准和精确配准。初始配准是为精确配准提供初始变换矩阵；精确配准是基于初始变换矩阵进一步得到更精确的解，从而提高配准精度。精确配准多采用迭代最近点（ICP）算法［1］，其具有极高的配准精度的优点，但需要良好的初始变换矩阵，否则两点云之间的转换较大会影响ICP迭代收敛过程，使其陷入局部最优解。因此选择合适的初始配准算法决定了配准效果。常见的初始配准算法有点云直方图算法［2］、快速点云直方图算法［3］以及三维形状上下文算法，其中三维形状上下文算法可求得更优的初始变换矩阵。

三维形状上下文（3DSC）是Belongie等［4］是在二维形状上下文［5］的基础上拓展得来的，并将其用于目标形状之间相似性识别。形状上下文配准在计算机图像学领域引起了广泛关注。Körtgen等［6］尝试将3DSC应用于三维形状检索和匹配。形状上下文极大地简化了源形状和目标形状之间点的对应关系，可以作为形状相似性的可靠描述。经研究比较，基于形状上下文的描述符对噪声场景具有较高的识别率。3DSC描述符结构简单、分辨力强，并且在杂乱场景上优于其他描述符。

形状上下文引入三维对象，将一个空间点上的形状上下文用于捕获周围空间其他点相对位置上的分布，进而可以通过局部丰富的描述来总结全局形状和鉴别全局特征。相似性的度量一般通过两个形状上的对应关系来估计其对齐变换矩阵，两个相似形状上的对应点具有相似的形状上下文。3DSC具有缩放、旋转和平移下的不变性以及描述能力，为三维对象之间的相似性度量提供了基础。配准是三维任务的关键，21世纪以来，国内外学者针对3DSC的配准做了很多研究。Kokkinos等［7］提出了三维形状的内在形状背景（ISC）描述符，将形状上下文中使用的图像域极性采样推广到曲面上，利用内在形状进行分析并基于最先进的密集形状描述符构造ISC，实现了在标准基准上形状匹配的显著改进。Li等［8］基于内在形状上下文针对特征点提出了一种独特的多尺度形状背景（MSC）等尺度的三维形状描述和配准方法，通过对一个稀疏特征点集的检测验证了其在两个公共基准上的性能有显著提高。Liu等［9］为了更好地实现轨迹分类的全局不变性，采用球形邻域将形状上下文自然地扩展到时空域，利用形状上下文的自适应外半径进行三维形状特征的提取。该方法的有效性为3DSC匹配方法中特征的提取提供了有利的证明。Xu等［10］结合内在形状特征（ISS）和3DSC提出了一种改进的迭代最近点算法。采用体素网格滤波器进行降采样，然后利用ISS算法提取特征点并由3DSC描述进行粗配准，最后利用迭代最近点算法进行精确配准。实验结果表明，该算法具有更快的配准速度，同时保持了较高的配准精度。

随着3DSC理论的深入研究与完善，3DSC配准方法逐渐在实际生产生活中拓展应用。卜琰等［11］为解决自动化装配中工件自动上下料时匹配识别困难的问题，提出一种基于改进形状上下文特征的工件识别和定位算法，利用形状上下文的形状识别方法检测工件的外形轮廓，在复杂环境下进行配准从而满足了工业作业中的技术需要。实验结果证明，基于形状上下文的识别匹配方法能够适应复杂的环境，有着很高的精度，能精准地对工件识别匹配。訾玲玲等［12］提出采用形状部件的上下文语义关系进行功能识别的方法，解决了当三维形状的几何特征和拓扑结构发生较大变化时形状部件的自动识别问题。实验结果表明，相比于已有方法，采用形状部件的上下文语义关系进行功能识别的方法可取得更高的部件匹配准确率和更低的分类错误率。Zhu等［13］提出一种基于3DSC的测量手势相似度的方法，并将其用于手势识别匹配，为3DSC匹配的发展运用提供了方向。文献［14］和文献［15］对PFH、FPFH和3DSC进行了对比分析，计算了点云的配准时间和配准误差，从数据分析中体现出3DSC方法的高精度配准性能，为高精度行业机器视觉引导指明了研究方向。由于3DSC配准时间比较长，其仅适合点云数据量比较少的形状配准。

3DSC的高精度配准要以牺牲配准时间为代价。针对3DSC配准效率，近年来也有学者进行研究并提出改进方法。文献［16］和文献［17］提出了两种快速形状检索的算法用来快速修剪搜索相似的形状，但是快速形状检索的算法本质是对图像进行多个块采样并求其配准成本，选择其中配准代价最小的样本，错误率达到了10%~14%，对于生产制造行业中高精度工艺并不适用。文献［18］展示了如何部署一个独特的局部参考系来提高3DSC描述符的准确性和减少内存占用，其主要是提升抗噪能力，减少噪点数据占用内存和噪点对配准精度的影响，针对噪点较小点云图像的优化并不明显，与传统3DSC并没有太大差异。另外随着计算机的发展，也有人提出以GPU并行方式配准运算的方法，但是效果有限。为进一步提高3DSC的配准效率且不失配准精度的高性能，点云图像数据的处理［19］、边界点云的采集方式［20］以及如何优化3DSC算法是难点，也是重点［21］。

本文提出改进的3DSC-ICP点云配准方法，通过改进轮廓点云降采样方式实现对三维形状轮廓特征的提取，对采集的点云依次进行三维网格划分形成3DSC进行改进的3DSC初始配准，将丢失的精度通过ICP精确配准补足，实现了源点云与目标点云之间的旋转平移变换，3DSC配准的速度和精度得到了提升，在提高3DSC配准效率的同时，也解决了ICP配准算法陷入局部最优的缺点。

2 三维形状上下文描述符

2.1 二维形状上下文向三维的扩展

在二维形状上下文中，基于二维对数极坐标系建立点直方图，如图1（a）所示。在3DSC中，通过构建基于三维球坐标系的点直方图，将二维形状上下文描述符扩展到三维空间，如图1（b）所示。传统的坐标利用笛卡尔坐标中的x、y、z来表示点云的每个位置，三维中可以用球坐标表示如下：

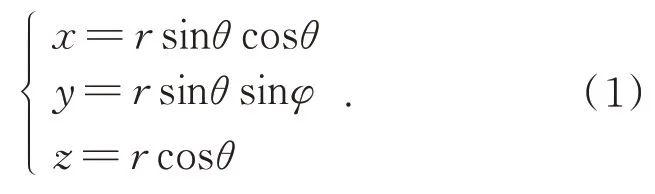
图1 二维形状上下文转三维形状上下文Fig.1 2DSC extends to 3DSC

一般来说，一个3DSC描述符可以用5个参数来描述：沿方位角维度的θ、沿径向维度的r、沿高程维度的φ、外半径和内半径（外半径为3DSC球中最外球的半径，内半径为3DSC球中最内球的半径）。笛卡尔坐标中各点的（x、y、z）位置可在球坐标中转换为（r、θ、φ），如式（2）所示：

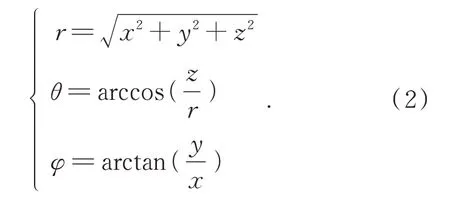
2.2 三维形状上下文描述符

3DSC使用向量（指定点的描述符）描述指定点及其在曲面上的形状特征，并通过匹配向量的值建立不同曲面点之间的对应关系。3DSC描述符具体构造方法如下：

（1）在以指定点P为中心的球面支撑域中，将网格划分为3个坐标方向：径向、方向角和俯仰角；

（2）计算落入网格的点数，并构造向量V（点P的描述符），V的每个元素对应于三维域中的一个网格，元素的值是相应网格中的点数。3DSC网格划分如图2所示。

图2 三维形状上下文网格划分Fig.2 3DSC meshing

3 改进的3DSC点云配准

3.1 改进的3DSC

传统形状上下文配准对于形状轮廓采样一般使用全采样、随机采样和平均采样的方式。全采样方式点云数据量大，配准效率慢；随机采样和平均采样的方式会丢失轮廓中具有重要形状特征的点云数据。

本文设计了阈值降采样方式（图3）提取3D图像的边界点云，以其中某一点云为起始点0，逆时针方向对边界点云排序，并对邻近两点云进行向量描述，向量夹角记为βi，阈值即为βi≤π），阈值范围为

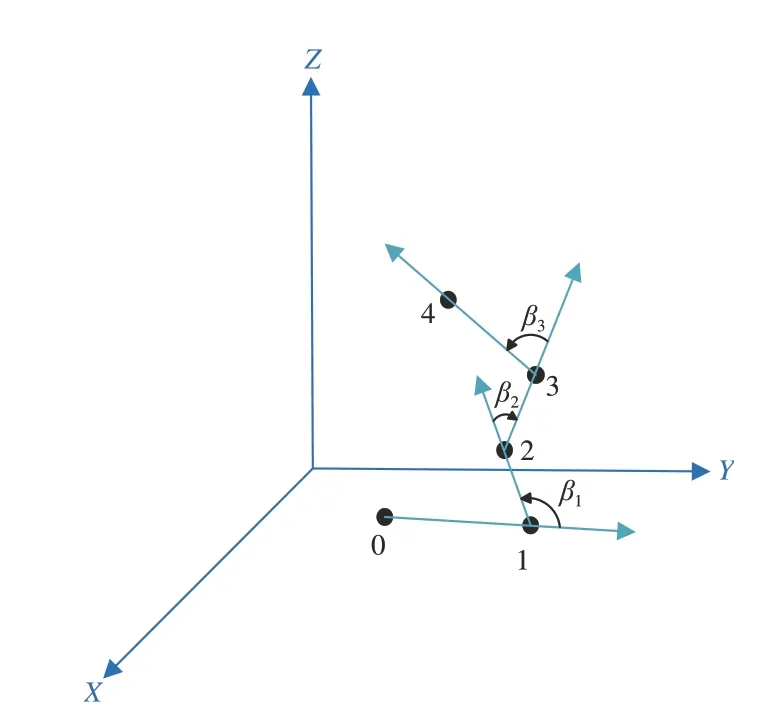
图3 三维形状上下文轮廓降采样Fig.3 Downsampling of 3DSC contours

给定阈值后即可根据向量角度大小对边界点云进行筛选采集，提取边界点云中更具特征的点云。

假设有λ个轮廓采样点组成的集合P=｛p1，...，pλ｝，以第i个采样点pi为坐标原点，按照r、θ、φ将三维球域划分成J×V×W个栅格，其中r的计算方法如式（3）所示：

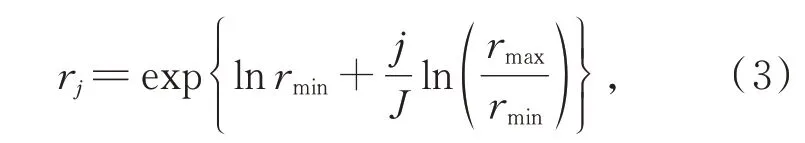
其中rmin为三维网格划分中最小球半径，rmax为三维网格划分中最大球半径。

然后用直方图来表示其余采样点的分布情况。设hi（k）为形状上下文特征，则：

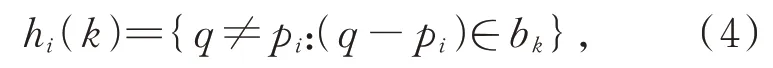
其中：q为剩余的采样点；bk为第k个栅格，1≤k≤J×V×W。

对于任意两个点m和n，m属于源点云形状点集，n属于待配准点云形状点集，点m与点n的形状上下文可以表示为直方图hm（l）和hn（l），其中l={1，2，…，L}是栅格的数量。由此可求得源点云形状和待配准点云形状的相似性度量，即可通过使用χ2来表示的两个直方图之间的成本代价Cmn：

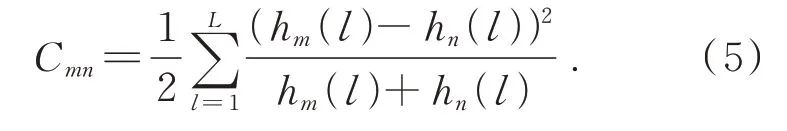
两个形状上下文的成本值较低意味着两点之间的相似性较高。

对于曲面配准，将一对点上的形状上下文方法应用于来自两个相似曲面（例如源点云形状和待配准点云形状）的一对点集，并应用于寻找两组点之间是否存在点对应。与源点云形状的点和待配准点云形状的点之间的每个对应关系可通过式（5）求得。对于源点云形状中的每个点，待配准点云形状的所有点都有相应的成本。考虑到待配准点云形状中的所有点，可以在这两个形状之间定义一个代价矩阵。理想的一组对应关系会使相应成本代价的和最小化。这是待配准点云形状中的点集，类似于源点云形状中的相关点集，可以表示如式（6）所示：

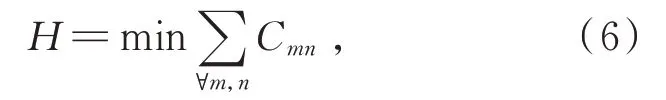
式（6）的结果是从所有可能的匹配点对的成本求和中找到的成本和最小的一个，因此，本文选择相似度高的匹配点作为最终的对应点。

3.2 点云配准

将获取的待配准点云进行预处理（欧式聚类提取、半径滤波），提取目标并去除图像中的噪点。然后设定阈值，通过改进的降采样方式采集轮廓点云，对采集的点云依次进行三维网格划分形成3DSC。接着进行改进的3DSC初始配准，找到对应的匹配点之后，便可以使用SVD算法求解在这种匹配下的旋转和位移矩阵。获得最优初始变换矩阵后，通过所求的旋转平移矩阵更新点云初始位置。至此初始配准完成，进而采用ICP算法进行精确配准。

通过ICP算法寻找待匹配点云和目标点云之间距离最近的点对集，然后通过最小二乘法迭代计算点对集的最优刚性变换参数。ICP算法的具体实现流程如下：

（1）给定两个点云集：

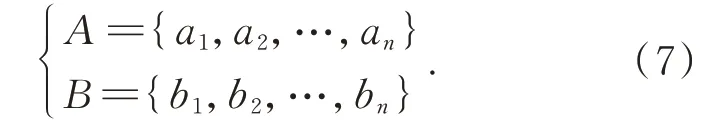
A和B之间存在某种旋转关系R和平移关系T，求解R和T使点对集中对应点的误差E最小。

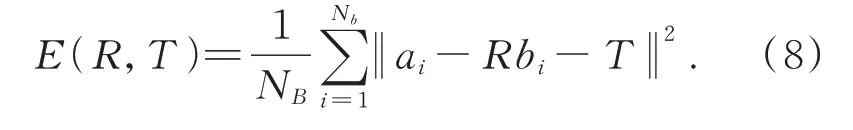
（2）寻找A和B中距离最近的点对集，以此计算R和T。根据R和T计算对应点误差。

（3）若误差未达到要求，则继续迭代直至满足误差要求；若误差达到要求，则终止迭代，输出最优解R和T。

改进的3DSC-ICP配准算法流程如图4所示。

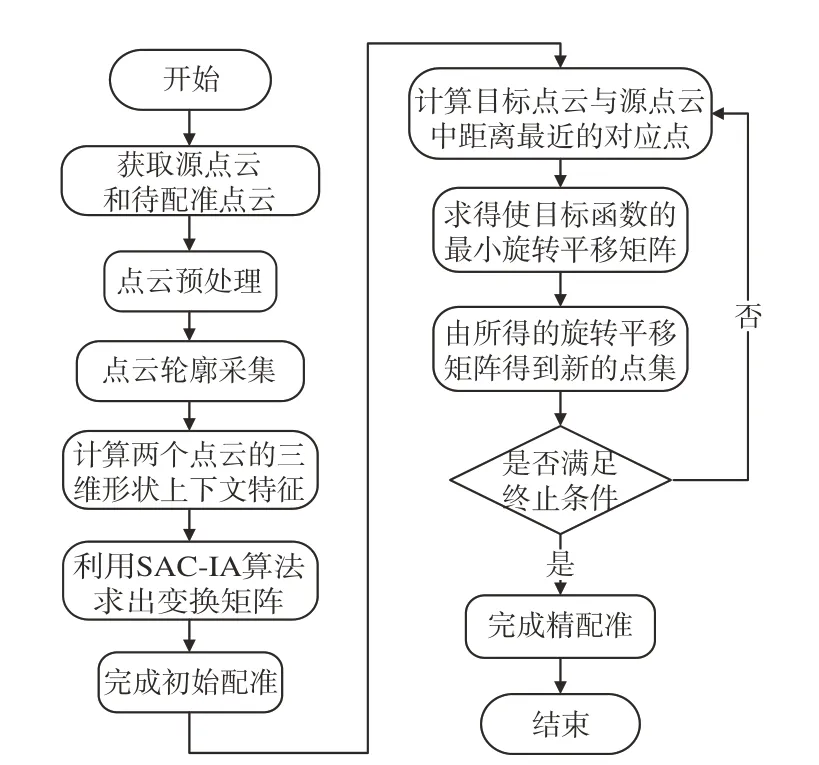
图4 改进的3DSC-ICP配准算法流程Fig.4 Flow chart of improved 3DSC-ICP registration al⁃gorithm

4 实验与分析

4.1 实验环境

将本文配准算法与经典PFH、FPFH以及传统形状上下文配准算法进行对比实验，从数据预处理、配准结果和配准误差3方面进行对比分析，以验证本文配准算法的优越性。

系 统 环 境：Windows 10专 业 版64位；硬 件环境：Intel Core i5 6300HQ 2.5 GHz，16G内存；开发环境：Visual Studio 2019。实验数据：（1）斯坦福兔子（Bunny）：源点云数目40 256，目标点云数目35 336；（2）kinect 3D相机拍摄的花盆点云（Flowerpot）：源点云数目74 994，目标点云数目70 336。

4.2 点云配准显示

4.2.1形状轮廓点云降采样显示

形状轮廓点云降采样如图5与图6所示。3DSC配准算法即对轮廓点云进行采样，以轮廓点云形成形状上下文进行配准。3DSC的配准精度高但配准时间较长，减少其配准时间有利于该配准方法的推广应用。本文设计了阈值降采样方式，设定阈值将源点云轮廓进行采样，如图5（c）和图6（c）所示。相对于全采样方式，形状轮廓点云降采样可有效减少轮廓点云数量。将点云图像轮廓以阈值降采样，既不失形状特征，又可简化形状上下文的运算，达到减少配准时间的效果。

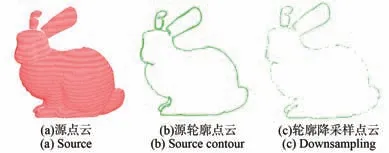
图5 斯坦福兔子形状轮廓点云降采样Fig.5 Downsampling of bunny-shaped contour point cloud

图6 花盆形状轮廓点云降采样Fig.6 Downsampling of flowerpot shape contour point cloud

4.2.2改进的3DSC-ICP配准结果显示

采用常用的斯坦福兔子和花盆的点云图像进行配准实验，其中绿色点云为源点云，红色点云为待配准点云，蓝色点云为已配准点云。配准结果如图7和图8所示，蓝色点云图与红色点云图的重合度体现了配准的效果。改进的3DSC配准算法克服了传统3DSC算法配准时间长的局限性，在有失配准精度的初始配准下，通过ICP精确配准保证了配准精度，提高了3DSC的点云配准效率。

图7 斯坦福兔子配准结果Fig.7 Registration result of bunny

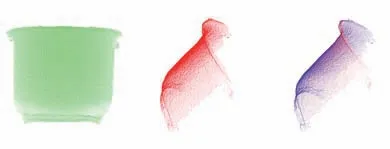
图8 花盆配准结果Fig.8 Registration result of flowerpot

4.3 数据分析

基于斯坦福兔子和花盆点云图像进行配准数据分析，将本文改进算法和传统3DSC方法进行对比。表1数据对比显示，通过设定阈值可有效减少轮廓点云数量，保留轮廓形状特征的同时也减少了配准时间。表2为配准方法的配准时间和配准精度比较。本文算法相对于传统3DSC方法在时间上得到了明显的优化。针对斯坦福兔子和花盆点云图像，传统3DSC算法配准时间为151.676 s和146.236 s，本文算法将配准时间降到28.181 s和20.856 s，节省了近75%~85%的配准时间。表2和表3将本文改进的3DSC-ICP配准方法与FPFH-ICP、PFH-ICP以及传统3DSC配准方法相比较，配准精度可提高2~3倍，本文改进算法配准误差、配准精度占有绝对的优势。实验证明本文改进的3DSC-ICP配准算法具有很大优越性，改善了3DSC的配准效率。

表1 数据预处理对比Tab.1 Comparison of data preprocessing

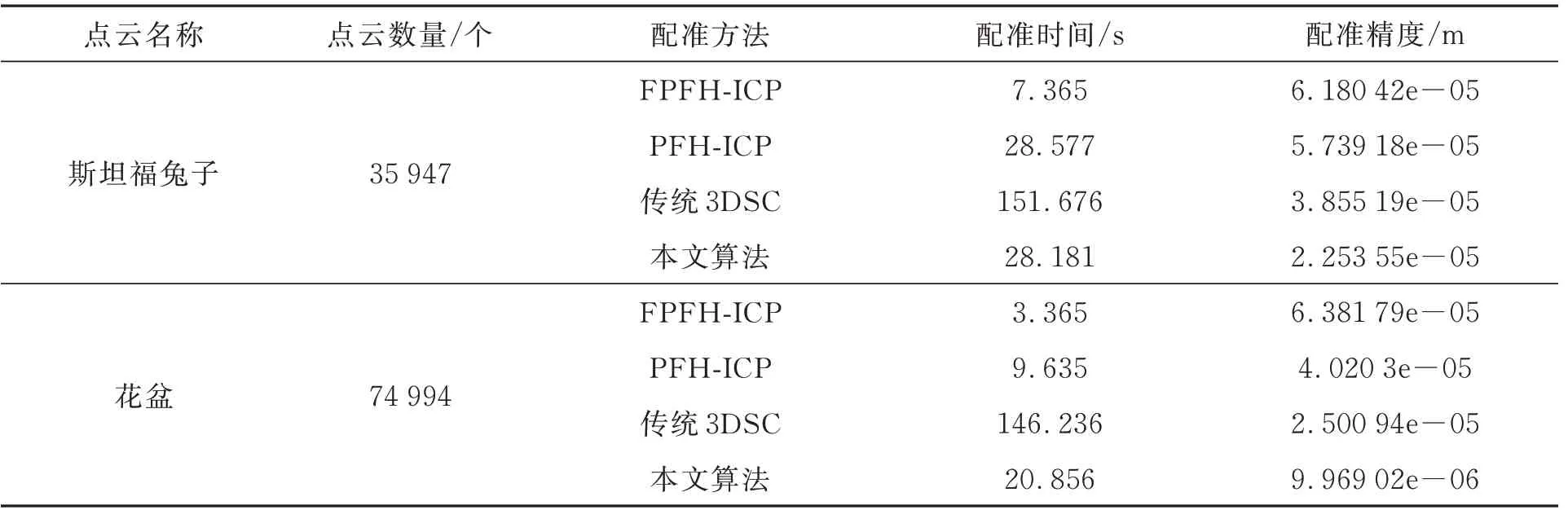
表2 配准时间和配准精度对比Tab.2 Comparison of registration time and registration accuracy

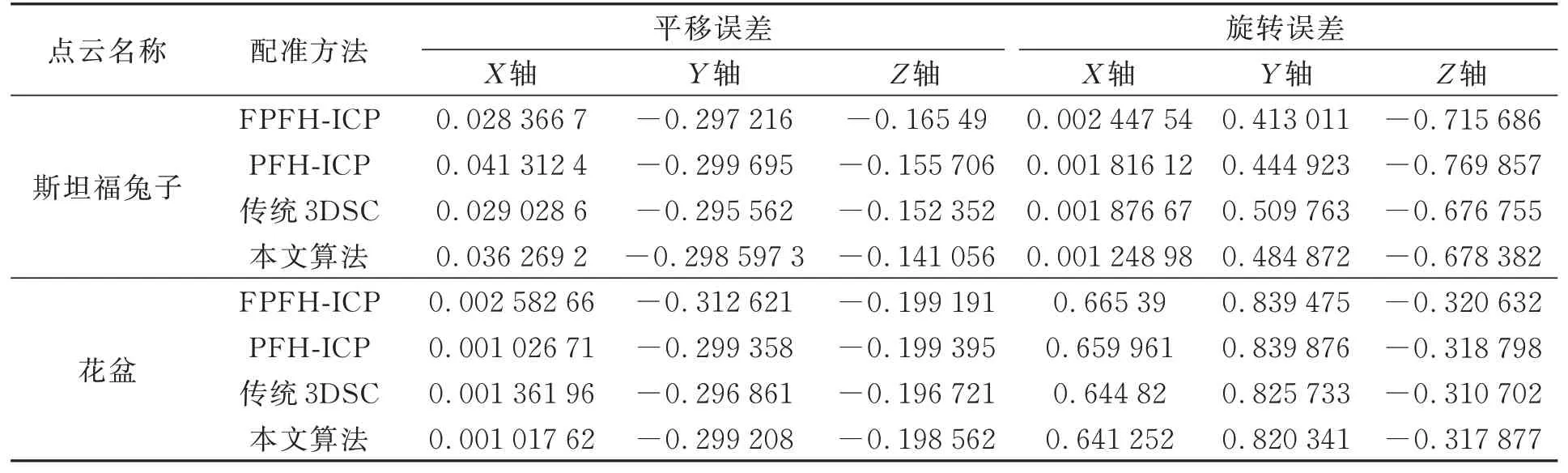
表3 配准误差对比Tab.3 Comparison of registration errors

5 结 论

3DSC以采集三维形状轮廓点云为基准，对每个采集点云进行上下文描述，若轮廓点云密集且数量集很大，数据运算量将会严重影响配准效率。对轮廓点云集以合理方式进行采样，有助于提高配准速度，减少配准时间。经典的3DSC一般以全采样或平均采样的方式进行采样，从而形成形状上下文，也有对轮廓点云归一化处理的研究。平均采样和归一化的研究方法虽然能够优化配准时间，但是配准精度却是大打折扣，以至于这些方式并不能广泛应用。本文对于三维形状轮廓点云改进采样方式，可针对不同的应用场景设置采样阈值，对轮廓点云集中角度变化较大的点云进行采集，保证了轮廓图像形状，有助于提高配准效率。本文提出的改进3DSC的配准算法在配准精度和配准时间上可做出平衡选择，降低轮廓采样减少传统3DSC配准时间的同时通过ICP精配准补足了配准精度的缺失。与传统3DSC配准算法相比，改进的3DSC配准算法可节省75%~85%的配准时间；与常用的PFH-ICP、FPFH-ICP配准算法相比，配准精度可提高2~3倍，为机器视觉在工业生产制造中开拓更广应用的同时也验证了3DSC配准在高精度工业运用的可能性。