一道IMO42不等式试题的探讨
2022-11-24冯光文云南省昭通市第一中学657000
中学数学杂志 2022年4期
冯光文 (云南省昭通市第一中学 657000)
本文从一道IMO42不等式试题说起,谈谈如何运用多种方法进行证明,并通过迁移和变通解决新问题,看清问题的源与流.




评注证法1两次运用柯西不等式,通过不等式的放缩进行转化,利用差值比较法以及n元均值不等式实现证明.

还有其他的变形方法,留给读者思考.





与问题2如出一辙,可用问题2的方法对其进行证明.文[3]中对②式用了五种方法证明,其本质上还是待定系数、去分母转化等.有些资料中有如下的问题:

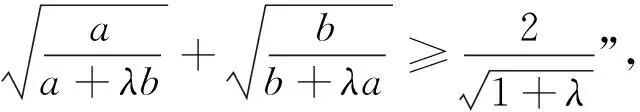

问题3(2007年台湾地区竞赛题)设a,b,c为正实数,证明:
分析 与问题1对比发现,其结构一样,只不过分母根号内的系数由8变为9,这导致了两个不等式的下界不同.问题1有多种思考策略,本题亦如此,当然可以利用权方和不等式来证.

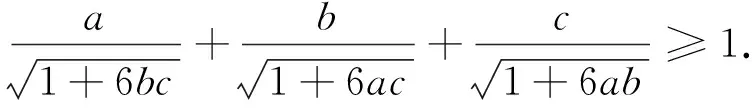
不难发现与问题1不同的是增设了一个条件a2+b2+c2=1,其他是一样的,可沿用问题1的方法解决,留给读者思考.我们还可以将上面的问题推广到下面的问题4.


问题5(2004年波兰数学奥林匹克试题)设a,b,c,d是正实数,证明:
分析 显然该不等式是对上面所讨论不等式的拓展,其结构与问题1~4类似,在文[1]中还是利用待定系数法对其进行证明.我们仍用权方和不等式进行证明.

问题1~5探讨了同源问题的来龙去脉,利用权方和不等式统一证明了这一系列的问题,同时还对其进行推广,获得了相应的结论.数学解题的核心素养就在于学会“观、思、变、论、推、创”,这样才学得灵活,学得透彻,学得富有新意.
