基于GA-BP 神经网络的极端降水定量分析与预测

赵奕昕，李 薇，朱家明

（1.南京师范大学 电气与自动化工程学院，江苏 南京 210023；2.南京师范大学 数学科学学院，江苏 南京 210023；3.安徽财经大学 统计与应用数学学院，安徽 蚌埠 233000）

近两年来，河南、陕西、湖北等地遇到了极为罕见的强降雨天气，对当地人民的生命和财产安全构成了严重威胁，严重影响了生产和生活。以郑州市为例，2021 年7 月18 日18：00 到21 日0：00，出现暴雨和特大暴雨，累计平均降水量为449 毫米。相关研究显示，在全球气候变暖的背景下，我国未来降水的数量、强度、频率和类型都将受到影响。预计在本世纪末，降水量将增加约10%，极端降水的概率将大幅增加。由于我国幅员辽阔，在各种类型地形和地貌的综合影响下，不同城市的降水特征呈现出不同的特点。因此，当务之急是建立一个可以通过不同天气特征变量来预测潜在极端降水事件的定量预测模型。对于降雨量的预测有多种方法［1-3］，本文选择基于神经网络对降水量进行定量预测。

1 数据来源及假设

数据来源于2021 年第七届数维杯国际大学生数学建模挑战赛B 题。其中，郑州市近10 年的气象数据由题目提供，南京市、太原市、北京市、上海市和广州市近10 年每隔3 小时的气象数据来源于世界天气数据网站https：//rp5.ru 和《中国统计年鉴》。为便于解决问题，提出以下两条假设：（1）假设剔除所给数据中的部分损坏或无关数据对模型研究不产生影响；（2）假设对于其他未提及的分子描述变量或因素，不影响模型研究。

2 基于皮尔逊相关系数的气象特征变量筛选

2.1 研究思路

由于所下载天气数据集是5 个城市近10 年每隔3 小时的气象数据，并且每个城市某一时刻的降水量与49 个不同的气象特征（如：大气湿度、大气压、风速、能见度等）有关，若将每一时刻的降水量和49 个变量全部导入神经网络进行训练，模型维度过高，将导致训练速度慢，训练效率低下。因此，需要对49 个气象特征变量进行选择，筛选出前7 个对降水量具有显著影响的气象特征变量。首先，对数据进行预处理，剔除数据缺失或无变化的气象特征变量。然后，采用皮尔逊相关系数（Pearson correlation coefficient）法建立反映变量之间相关关系密切程度的模型，展示不同气象特征变量对降水量的影响强度，取降水量与预处理筛选出来的气象特征变量进行相关性分析，得到降水量与各气象特征变量之间的相关系数，进而对相关系数的绝对值进行排序，取排名前7 名的变量，即对降水量最具影响的前7 个气象特征变量，有利于减少数据冗余，提高神经网络运算效率。

2.2 研究方法

2.2.1 数据预处理 通过观察5 个城市近10 年每隔3 小时的气象数据表格，发现在49 个气象特征变量中，部分变量数据缺失或变量值均为999.9，虽然数据缺失或均为同一数值并非没有实际意义，有可能是该变量无法观测，但显然对降水量的影响程度较低，为减少后续计算量，先将这些变量剔除，可视作这些气象特征变量对降水量几乎无影响。同时，对没有降水量数据的时间点，删去气象数据。因此，后续只需对余下的38 个气象特征变量进行排序筛选。

2.2.2 皮尔逊相关系数分析 皮尔逊相关系数可用于度量两个变量之间的相关程度［4］，本文采用皮尔逊相关系数来描述不同气象特征变量与当前时刻降水量的相关性。本文的天气数据是5 个城市近10 年每隔3 小时的气象数据，样本容量近30 000 个，结果具有一定的普遍性，可以运用相关系数判断其相关性。

用MATLAB 软件计算38 个气象特征变量与降水量值的皮尔逊相关系数，并对计算结果的绝对值进行排序，得出前7 个对降水量最具有影响的气象特征变量，变量筛选结果与各变量含义见表1。

表1 前7 个对降水量最具影响的气象特征变量Tab.1 Top 7 most influential meteorological characteristic variables on precipitation

上述7 个气象特征变量与降水量的相关系数热力矩阵图如图1 所示（其中，RRR为降水量）。

图1 相关矩阵热力图Fig.1 The map of related matrix heat

3 基于GA-BP 神经网络的降水量预测分析

3.1 研究思路

根据降水量（因变量）与7 个气象特征变量（自变量）之间的对应关系，通过神经网络模型来拟合这种非线性逻辑关系，构建某一时刻降水量的定量预测模型。将经过处理的5 个城市近10 年的气象数据导入MATLAB 软件，构建神经网络模型，建立7 个自变量与1 个因变量之间的非线性关系。通过多次训练与优化，生成能根据气象特征变量准确预测降水量的定量预测模型。

3.2 GA-BP 神经网络

3.2.1 BP 神经网络 人工神经网络（artificial neural networks，ANN）是由大量的处理单元（神经元，neurons）广泛互联而成的网络，是对大脑的抽象、简化和模拟，反映人脑的基本特性，适合处理非线性拟合问题。它是由简单的处理单元所组成的大量并行分布的处理机，这种处理机具有储存和应用经验知识的自然特性，它与人脑的相似之处可概括两个方面：一是通过学习过程利用神经网络从外部环境中获取知识；二是内部神经元用来存储获取的知识信息［5-6］。

使用误差反向传播算法（BP 算法）训练的神经网络，称之为BP 神经网络，1986 年由Rumelhart 和McClelland 为首的科学家提出的概念，是一种按照误差逆向传播算法训练的多层前馈神经网络，是应用最广泛的神经网络之一。在人工神经网络的实际应用中，BP 网络广泛应用于函数逼近、模式识别/分类、数据压缩等，80% 左右的人工神经网络模型采用BP 网络或它的变化形式。

应用BP 神经网络进行建模时，模型输入可以表示为xj(t) (j=1，2，…，N)，其中j表示输入量离散后的下标，N为离散量的总数；模型输出可以表示为tj(t) (j=1，2，…，N)，其中j表示输出量离散后的下标。对于降水量与7 个气象学变量之间的关系来说，模型的输入是7 个气象学变量值，模型的输出是对应降水量大小，需要注意的是模型的输入输出是严格对应的。

BP 神经网络为三层结构（图2），分别为输入层、隐含层、输出层。每一层神经元的个数可以不相同，输入层神经元与隐含层神经元之间有输入层权重w和隐含层偏置b连接，隐含层神经元与输出层神经元之间有输出层权重和输出层偏置的连接。

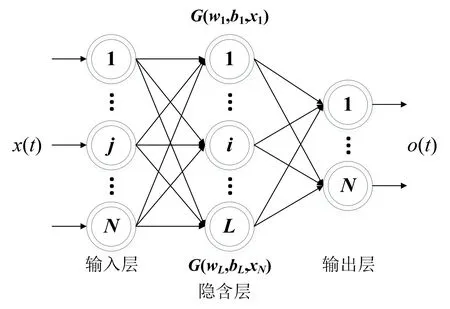
图2 BP 神经网络结构图Fig.2 The structure of BP neural network

对于任意N个离散的训练数据，具有L个隐含层神经元的单隐含层BP 神经网络为

其中：o(t)为网络的输出向量，x(t)为输入向量，bi(t)为每一个隐含层的偏置；wi(t)和βi(t)分别为输入层权重和输出层权重。g(·)代表激活函数，G(·) 为激活函数的详细展开，可以选取正弦函数、S 型函数、线性函数和硬限幅函数等类型函数。

神经网络的核心是不断更新参数(wi，bi) 和βi使得式（2）得以满足，即使tj和oj之间的均方差和尽可能小。

3.2.2 基于GA 优化的BP 神经网络 基于BP 神经网络教师学习算法虽然可以稳定得到权值，但学习收敛速度较慢，不一定为全局最优解，极易陷入局部极小模式。因此，需要对其进行优化。

遗传算法（genetic algorithms，GA）是模拟生物在自然环境中的遗传和进化过程而形成的一种通用性优化算法，由John H.Holland 教授提出。作为一种实用、高效、鲁棒性强的优化算法，其发展极为迅速，已成功应用于各个领域的优化问题，引起了国内外研究学者的广泛关注。遗传算法主要特点是群体搜索策略和群体中个体间的信息交换，搜索不依赖梯度信，简化计算过程［7-10］。

用遗传算法优化BP 神经网络，可对三个方面进行优化：连接权值、网络结构和学习规则。目前使用GA 进行BP 神经网络的优化主要是对连接权值w进行最优化选择，主要步骤如下：

（1）对不同结构（不同隐含层节点数量、层数）的神经网络进行训练与测试，选出最优神经网络结构；

（2）对最优结构的神经网络进行预训练一定次数，取得权值和阈值的取值范围[Umin，Umax]；

（3）初始化遗产算法种群，包括选择规模、交叉概率、变异概率及初始权值；

（4）计算种群中每一个个体的适应度值，并将其排序；

（5）进行染色体选择、交叉、变异，形成下一代种群；

（6）重新计算适应度值，判断最优个体是否满足终止进化的条件，若满足，则停止迭代并输出结果；否则，返回步骤4；

（7）更新BP 神经网络权值阈值，训练神经网络模型。

因此，结合遗传算法和BP 神经网络可以对网络初始的权值和阈值进行一定程度的优化处理，改进BP神经网络对初始权重依赖的问题。GA-BP 神经网络算法流程图如图3 所示。

图3 GA-BP 算法流程图Fig.3 Flow chart of GA-BP algorithm

3.3 模型的建立

将数据中的降水量数值和7 个相关气象特征变量数值U、Ff、Td、P0、P、VV和T一同导入MATLAB，训练BP 神经网络模型，进行多次训练并通过比较拟合优度系数选出最优的神经网络结构（图4）。

图4 神经网络模型简化图Fig.4 Simplified diagram of neural network model

如图4 所示，当隐含层数量设置为10，且为单隐含层时，BP 神经网络拟合效果最好，该训练模型有7 个输入变量与1 个对应的输出变量。其中，设置BP 神经网络最大训练次数设置为1 000，学习率设置为1e-3，训练目标设置为1e-6，输入层到隐含层传递函数使用双极性传输函数tansig，隐含层到输出层传递函数使用线性函数purelin，训练算法选择L-M（Levenberg-Marquardt）算法。将此BP 神经网络模型应用GA 算法进行进一步优化，得出最优权值阈值，再次进行训练。

将后100 组数据作为测试集，该GA-BP 神经网络模型对测试样本的预测结果如图5 所示。

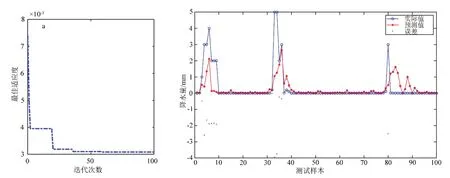
图5 对后100 个数据的预测结果Fig.5 Prediction results for the last 100 data

对测试集样本预测结果的拟合优度参数见表2。从表2 可知，该模型对测试集100 组数据的预测效果良好，确定系数R2达0.527。该GA-BP 神经网络模型对训练集数据的拟合情况如图6 所示。从图6可以看出，该神经网络模型对降水量大小的预测较为准确，能正确反应降水量的周期性变化规律，可用于城市降水量的预测。

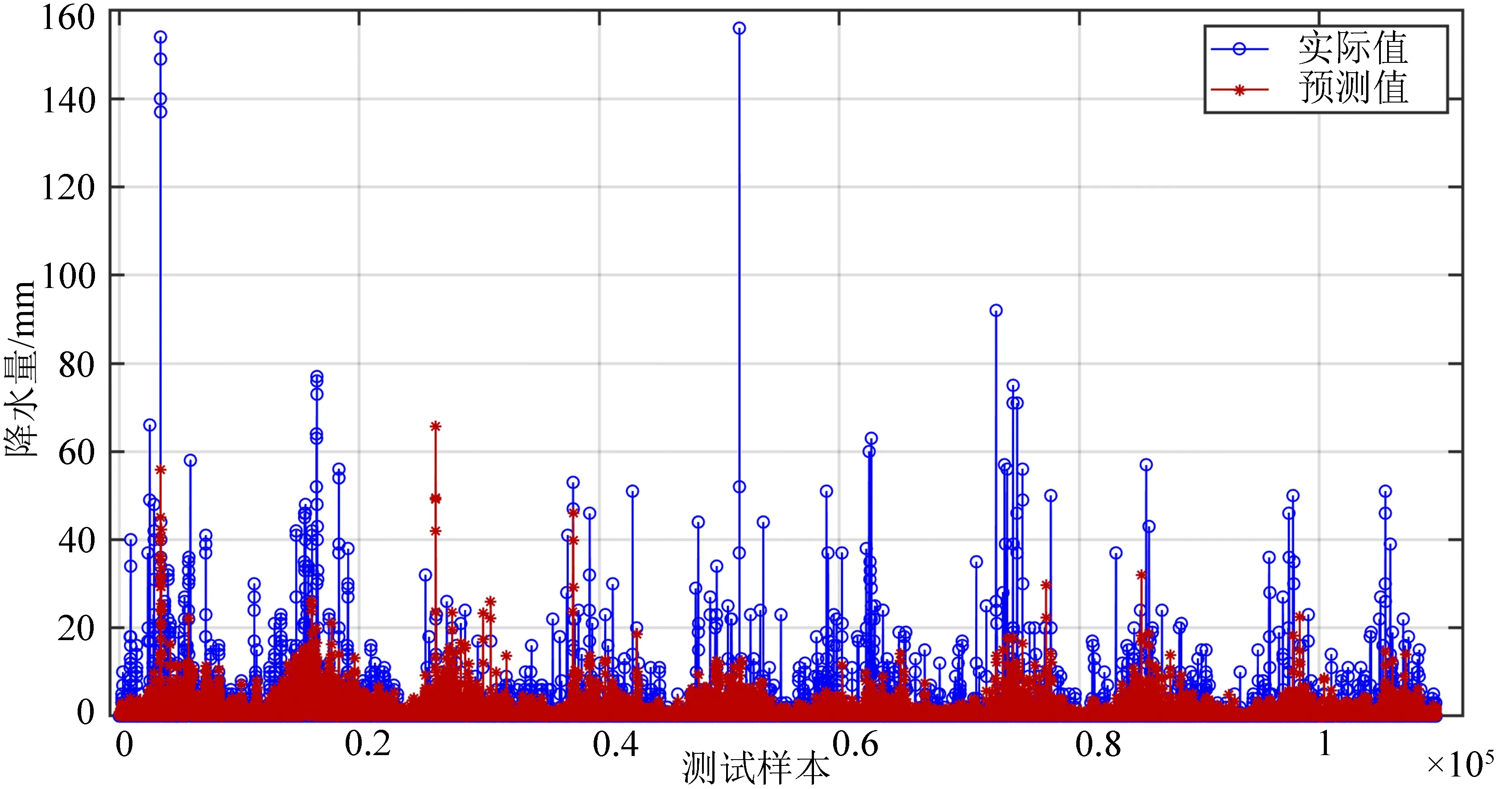
图6 对训练集数据的拟合Fig.6 Fitting to the training data

表2 拟合优度参数Tab.2 Goodness-of-fit parameters

3.4 模型的应用

以郑州市2021 年7 月份为例，将郑州市2021 年7 月1 日至2021年7 月31 日的天气数据中，7 个相关变量T、P0、P、U、Ff、VV和Td导入MATLAB，利用上述GA-BP 神经网络模型对降水量进行预测，结果如图7 所示。

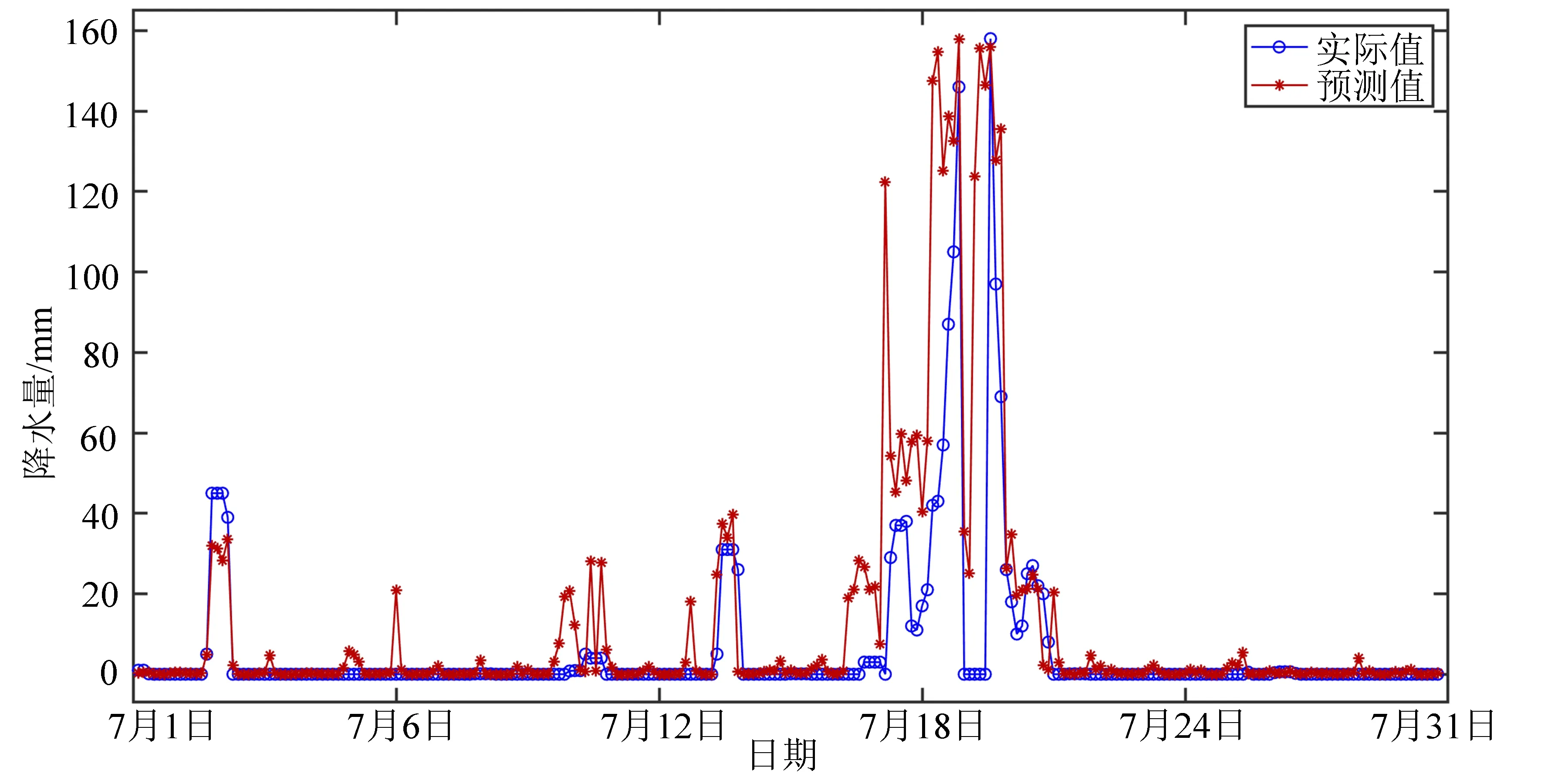
图7 郑州市2021 年7 月降水量预测结果Fig.7 Precipitation forecast results for July 2021 in Zhengzhou

从图7 可以看出，该模型能较为准确地预测郑州市2021 年7 月18 日到21 日的降水量猛增情况，对无降雨或降水量较少的天气也能较精确地预测。因此，该模型能够较为准确地预测极端降水天气，对极端降水预测和提前防范洪涝灾害具有重要意义。

4 结论

本文从南京市、太原市、北京市、上海市和广州市最近10 年的历史气象数据出发，采用皮尔逊相关系数法对每个城市年降水量与多个气象特征变量进行相关性分析，通过计算皮尔逊相关系数的绝对值，筛选出了前7 个对降水量最具有影响的气象特征变量。使用GA-BP 神经网络构建了7 个气象特征变量与降水量之间的非线性关系，通过训练得到了一个神经网络定量预测模型。以郑州市2021 年7 月份为例，利用训练得到的神经网络模型对降水量进行预测，结果显示该模型能较为准确地预测极端降水天气。对于重点城市的极端降水天气的预测与提前防范洪涝灾害具有重要意义和参考价值，同时，也可应用于气象数据分析时缺失值的精准补全。