（3+1）维B-type Kadomtsev-Petviashvili-Boussinesq方程的精确解

霍江映，套格图桑，2

（1.内蒙古师范大学 数学科学学院，内蒙古 呼和浩特 010022；2.内蒙古自治区应用数学中心，内蒙古 呼和浩特 010022）

0 引言

非线性发展方程在物理和数学方面的研究受到广泛关注。近些年，不同方法被用来求解非线性发展方程，从而获得非线性发展方程的精确解，包括齐次平衡法、贝尔多项式法、符号计算法和双线性变换法等。文献［1］使用符号计算法求解（3+1）维B-type Kadomtsev-Petviashvi（lBKP）方程的高阶怪波解；文献［2］利用齐次平衡法求得（3+1）维BKP 方程

的单孤子解和双孤子解。文献［3］使用（G'/G）展开法求（3+1）维Jimbo-Miwa（JM）方程

的单孤子解和双孤子解。

本文研究了包含上述两个方程的（3+1）维B-type Kadomtsev-Petviashvili-Boussinesq（BKPB）方程，并获得了包含指数函数、三角函数和双曲函数组合的精确解。

若对方程

取α=1，β=3，γ=1，η=0，δ=1，则可将其化为方程（1）；若方程（3）取α=-1，β=-3，γ=2，η=0，δ=-3，则可将其化为方程（2）。

1 （3+1）维BKPB 程的双线性化与精确解

1.1 （3+1）维BKPB 方程的双线性化

当β=3α时，通过变量变换

将方程（3）化为双线性形式

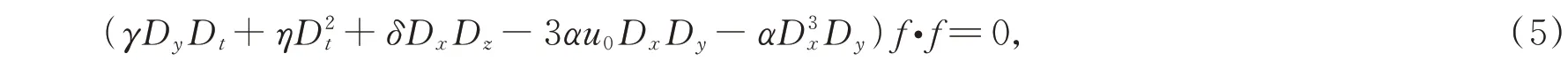
其中u0是待定常数。Dx，Dy，Dt和Dz是Hirota 双线性算子，其满足

1.2 （3+1）维BKPB 方程的精确解

引入试探函数

其中εj，μj，ai，bi，ci，di(i=1，2，3，4；j=1，2，3，4)是待定的常数。

将式（7）—（12）分别和式（6）一起代入变换（4）中，即可得到方程（3）的6 组如下精确解。

这里ai，bi，ci，di(i=1，2，3，4)由式（13）—（17）确定，另外，εj，μj(j=1，2，3，4)是任意常数。

当选取参数为α=1，γ=1，η=1，δ=3，a1=3，b1=1，c1=-1，u0=2，μ1=3，ε1=3 时，（3+1）维BKPB 方程的精确解u1可化为（解的情况见图1）

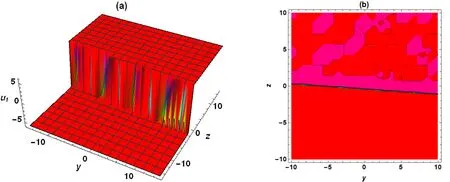
图1 当x=0，t=-2 时，（19）式关于y，z 的三维图和等高线图Fig.1 when x=0，t=-2，3D plot and contour plot related to y and z corresponding to formula（19）

当选取参数为ε2=9，ε1=2，a1=1，b1=2，b2=i，c2=i，d2=2i，μ1=4，μ2=0 时，（3+1）维BKPB 方程的精确解u2可化为（解的情况见图2）

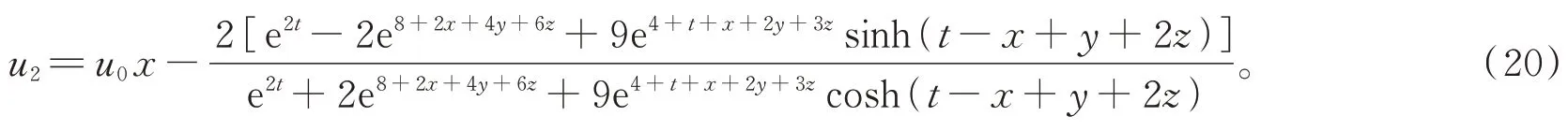
当选取参数为ε4=-2，ε1=1，a1=2，a4=1，b1=4，b2=-2，c4=1，d2=2，d4=-4，μ1=4，μ4=2时，（3+1）维BKPB 方程的精确解u3可化为（解的情况见图3）

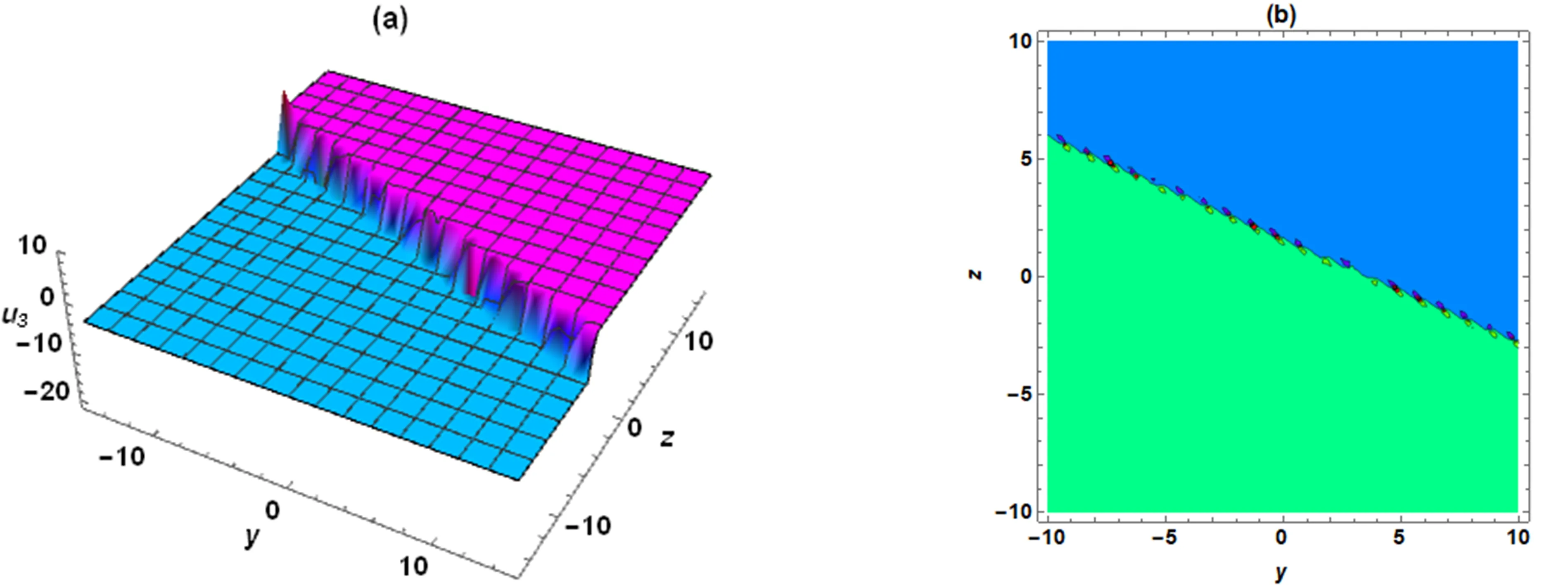
图3 当x=0，t=-2 时，式（21）关于y，z 的三维图和等高线图Fig.3 when x=0，t=-2，3D plot and contour plot related to y and z corresponding to formula（21）

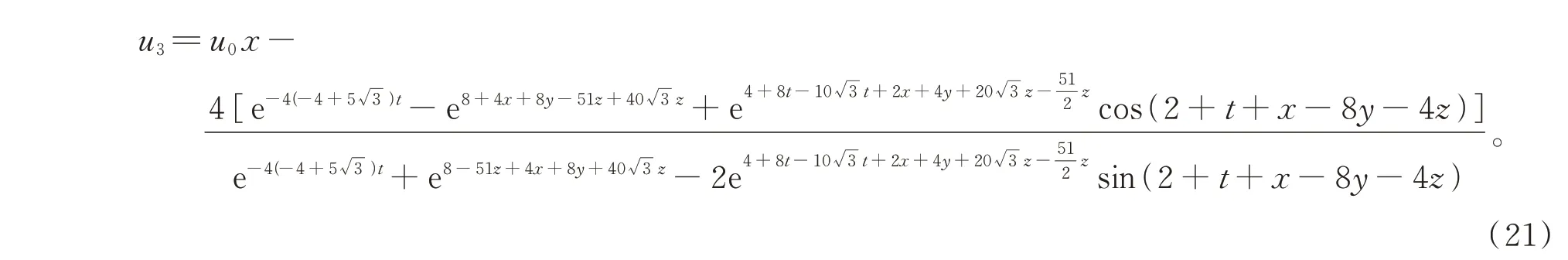
当选取参数为ε2=2，a1=12，a2=2，b1=11，c2=2，b2=3，d2=1，d4=-1，μ1=1，μ2=1 时，（3+1）维BKPB 方程的精确解u4可化为（解的情况见图4）

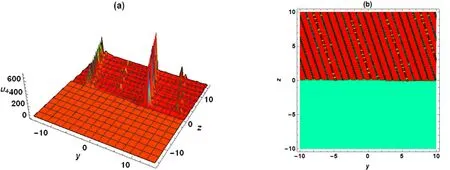
图4 当x=0，t=-2 时，式（22）关于y，z 的三维图和等高线图Fig.4 when x=0，t=-2，3D plot and contour plot related to y and z corresponding to formula（22）

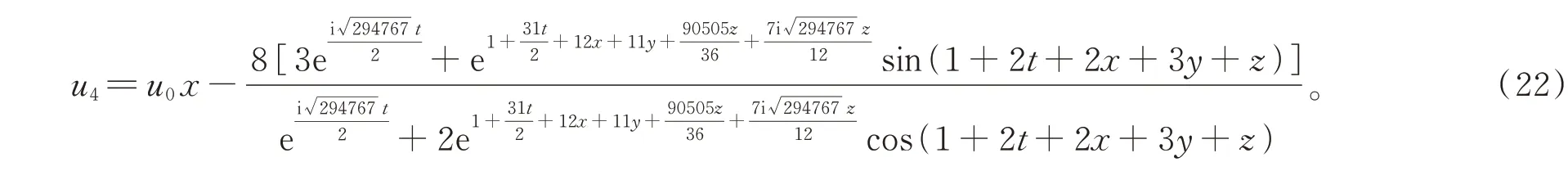
当选取参数为ε3=2，a1=2，a3=3，b1=-1，c3=1，b3=-2，d3=1，μ1=2，μ3=2 时，（3+1）维BKPB 方程的精确解u5可化为（解的情况见图5）

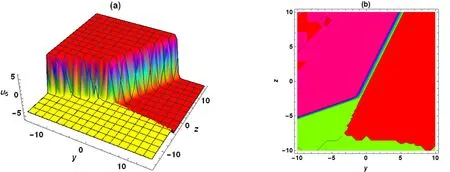
图5 当x=0，t=-2 时，式（23）关于y，z 的三维图和等高线图Fig.5 when x=0，t=-2，3D plot and contour plot related to y and z corresponding to formula（23）

当选取参数为ε1=5，ε4=2，u0=2，a1=-1，a4=1，b1=2，b4=1，c4=51，c1=1，d4=1，μ1=3，μ4=2 时，（3+1）维BKPB 方程的精确解u6可化为（解的情况见图6）

图6 当x=0，t=0.63 时，式（23）关于y，z 的三维图和等高线图Fig.6 when x=0，t=0.63，3D plot and contour plot related to y and z corresponding to formula（23）

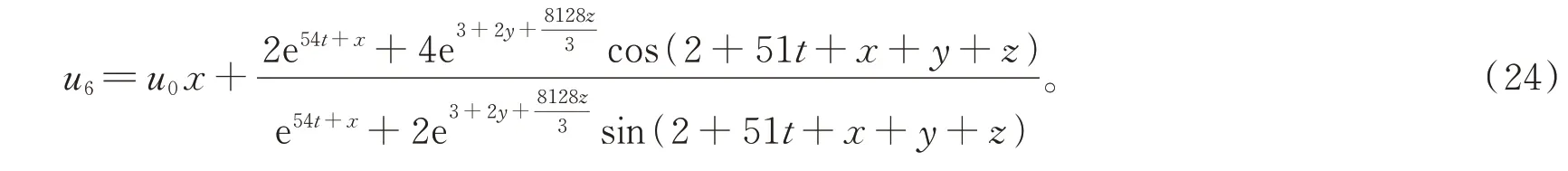
2 （3+1）维BKP 方程的精确解

利用上面的方法研究（3+1）维BKP 方程，当选取参数为α=1，β=3，γ=1，η=0，δ=1 时，（3+1）维BKPB 方程化简为（3+1）维BKP 方程

因此，当（7）式中选取参数为ε1=2，μ1=3，u0=-2，a1=1，a2=-1，b1=-1，b2=-2，c1=1 时，将其代入到解（13）后可以得到方程（1）的如下形式解（解的情况见图7）

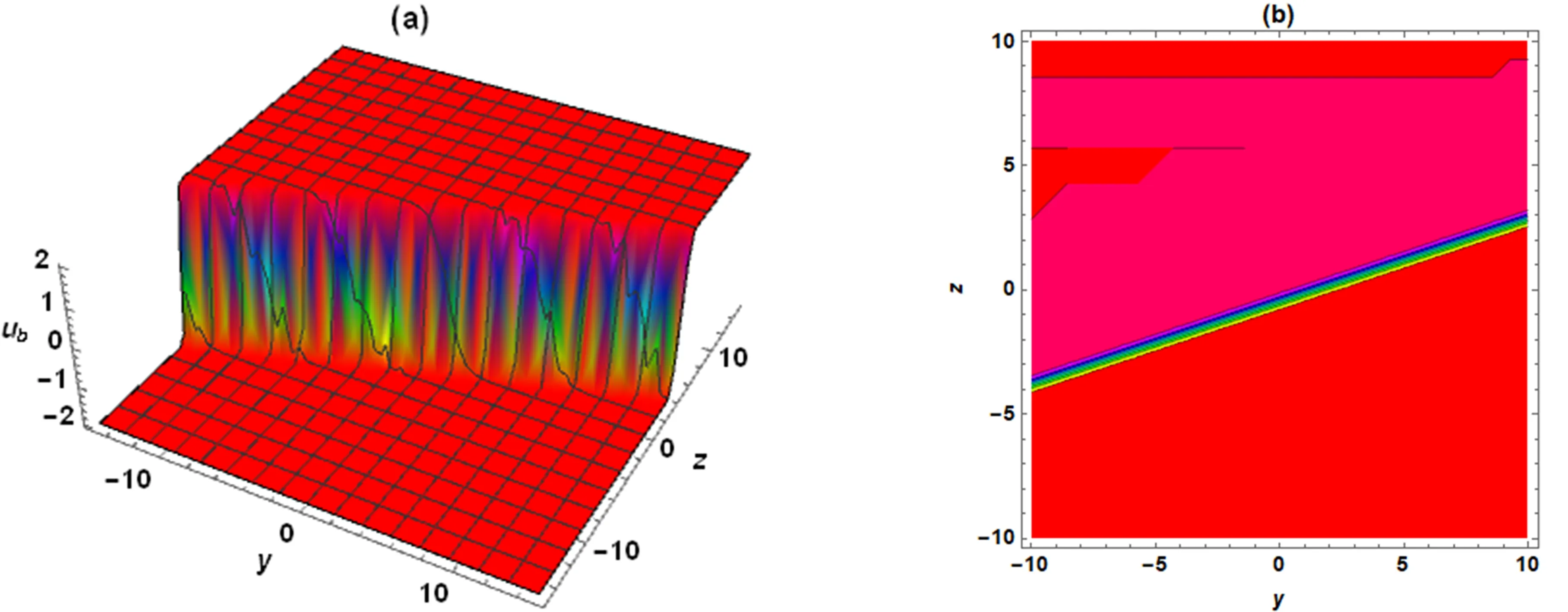
图7 当x=0，t=-2 时，式（25）关于y，z 的三维图和等高线图Fig.7 when x=0，t=-2，3D plot and contour plot related to y and z corresponding to formula（25）

3 （3+1）维JM 程的精确解

对于（3+1）维JM 方程，当α=-1，β=-3，γ=2，η=0，δ=-3 时，（3+1）维BKPB 方程可化为（3+1）维JM 方程

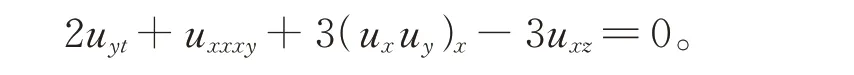
当（8）式中选取参数为a1=3，b1=1，b2=1，d2=-1，c2=2，u0=3，ε1=3，ε2=1，μ1=-3，μ2=2 时，代入解（14），可以得到方程（2）的如下形式解（解的情况见图8）

图8 当x=0，t=-1.3 时，式（26）关于y，z 的三维图和等高线图Fig.8 when x=0，t=-1.3，3D plot and contour plot related to y and z corresponding to formula（26）

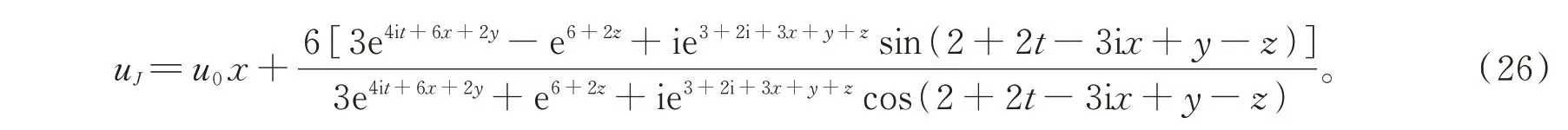
4 结论

本文基于广田双线性法和试探函数法，构造了（3+1）维BKPB 方程的一系列解，并利用符号计算系统Mathematica，对获得解的图像进行分析研究。此外，通过对方程（3）取不同的参数构造了（3+1）维BKP 方程和（3+1）维JM 方程的精确解，并分析了解其性质。

当u0=0 和μ1=μ4=0 时，方程（3）的解（15）可以化简为文献［15］得到的解u2(x，y，z，t)=当u0=0 和μ1=μ2=0 时，方程（3）的解（14）可化为文献［15］得到的解ε2cos(a2x+b2y+c2t+d2z)]}x；当u0=0 和μ1=0 时，方程（3）的解（13）可以化为文献［17］得到的解因此，文献［15］和文献［17］获得的结论是本文获得结论的特殊情况。