十次对称二维准晶矩形板面内非线性分布载荷下的弹性力学问题

张 静，李联和，2

（1.内蒙古师范大学 数学科学学院，内蒙古 呼和浩特 010022；2.内蒙古自治区应用数学中心，内蒙古 呼和浩特 010022）

0 引言

1984 年，Shechtman 等［1］发现了一种既具有晶体也具有非晶体特征的新型固体结构——准晶。2009 年，准晶的研究取得了突破性的进展——首次在自然界中发现了天然的准晶［2］。准晶由于其特殊的准周期对称性，使其弹性常数比经典弹性材料高，因而使得准晶力学问题的研究存在很多困难［3-6］。因此，科研工作者们采用了多种方法研究准晶材料的力学问题，促进了准晶材料的发展和应用。范天佑，李显方等［7-8］利用Fourier 变换法研究了准晶的裂纹问题和位错问题。高阳等［9］利用Stroh 公式研究了准晶含有椭圆孔口和夹杂的力学问题。李翔宇［10］利用位移势函数方法研究了准晶的平面裂纹问题。刘官厅［11］采用半逆解法研究了含椭圆孔口的准晶的反平面问题。李联和［12］利用复变函数方法研究了三维二十面准晶的平面弹性力学问题。郭俊宏等［13］利用Stroh 方法研究了一维准晶中由椭圆孔产生的四条裂纹的精确解问题。

准晶自发现以来，在很多方面都体现出优异的物理性能，如导热率低、抗氧性高和摩擦系数低等。准晶材料在实际工程中应用广泛。梁和板做为一种典型结构，一直都是固体力学研究的重点。关于准晶梁和准晶板的研究具有重要意义。在准晶梁和准晶板的研究方面，武亚楠［14］研究了二维十次准晶悬臂梁的弯曲问题。Huang 等［15］解决了功能梯度一维压电准晶层合板的相关电弹性问题。

本文利用微分求积法探究了点群10 mm 十次对称二维准晶板在边界受余弦分布载荷下的弹性力学问题，得到了准晶板的位移与应力分布情况，并讨论了材料参数对准晶板的弹性力学问题的影响。

1 控制方程及边界条件

1.1 控制方程

假设准周期平面为xy平面，十次对称准晶周期方向为z轴，根据准晶弹性理论［16］，有变形几何关系平衡方程（忽略体力的情况下）

广义Hooke 定律［17］

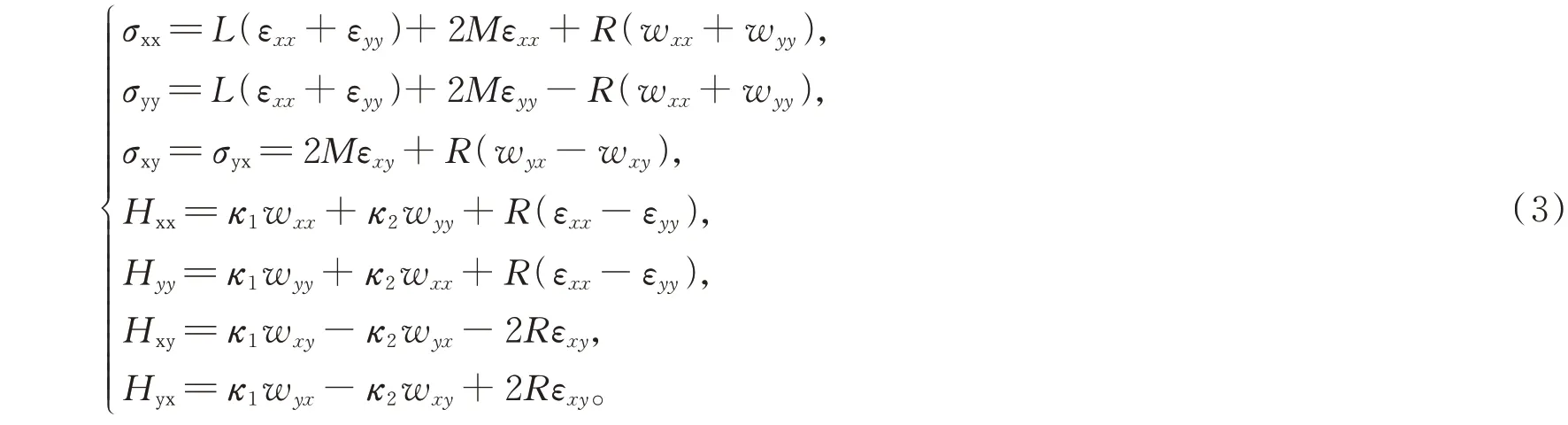
其中，L=C12，M=(C11-C12)/2。ux，uy，σxx，σyy，σxy，σyx，εxx，εyy，εxy，εyx，分别为声子场位移、应力和应变；wx，wy，Hxx，Hyy，Hxy，Hyx，wxx，wyy，wxy，wyx，分别为相位子场位移、应力和应变；C11，C12为与声子场有关的俩个非零独立的弹性常数；κ1，κ2为与相位子场相联系的俩个非零独立弹性常数；R为声子场和相位子场耦合的非零独立弹性常数。

由式（1）（2）（3）得到点群10 mm 十次对称二维准晶平面弹性问题的控制方程

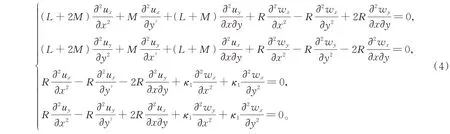
1.2 边界条件

考虑一个长度为a，宽度为b，厚度为h的受余弦分布载荷的点群10 mm 十次对称二维准晶的矩形板，如图1 所示。板边界承受非均匀分布的边缘载荷σx0=-σ0cos(πy/b)。

根据图1 所示，具有如下的边界条件

图1 边界受余弦分布载作用下的矩形板示意图Fig.1 Schematic diagram of rectangular plate with boundary under cosine distribution loading

2 点群10 mm 十次对称二维准晶的一般解

在微分求积法分析中，网格的划分极其重要。利用Gauss-Chebyshev-Lobatto 的分布定律，得到关于x和y的网格点分布式［18］，即

根据微分求积法［19-20］，控制微分方程（4）和边界条件（5）分别转化为

由于矩阵[K]的可逆性，式(10) 可以转换为式(12)，

通过计算式(12)，得到位移；将位移带入式(13)，得到准晶板的应力。

3 数值算例

3.1 本文算法可靠性检验

为了检验本文算法的正确性与可靠性，在不考虑相位子场的情况下，本文结果可以退化成文献［21］中的结果。例如，在表1 中，以正应力σxx为例，与文献［21］中结果进行对比，二者结果吻合。

表1 长宽比λ=1 时声子场正应力σxx 的值Tab.1 Normal stress σxx in phonon field with aspect ratio λ=1

3.2 结果与讨论

文中选取Al-Ni-Co 准晶为例讨论不同长宽比λ的矩形板对位移和应力的影响，弹性材料性质和几何参数如下［22］：C11=234.33 Gpa，C12=57.41 Gpa，κ1=122 Gpa，κ2=24 Gpa，R=0.885 Gpa，σ0=1。

声子场和相位子场的位移都是关于x和y的函数（图2）。根据准晶板的受力情况，其被施加的外力是属于声子场范畴的力，又由于准晶板声子场和相位子场的耦合，所以相位子场也相应存在着位移变化。同时，声子场和相位子场沿x方向的位移总是关于y/b=0 对称，沿y方向的位移总是关于x/a=0 对称。

图2 长宽比λ=1 的位移分布图Fig.2 Displacement distribution with aspect ratio λ=1

不同材料尺寸准晶板的声子场和相位子场的应力分布图，如图3-9 所示。声子场的正应力σxx，σyy和切应力σxy以及相位子场的正应力Hxx，Hyy和切应力Hxy，Hyx都呈现明显的非线性分布。其中，正应力σxx在板边缘x/a=-0.5 和x/a=0.5 处呈现先增大后减小的趋势，同时在y/b=0 处σxx达到最大值。随着板的长宽比不断增大，板内部的应力分布呈现出越来越平坦的趋势，但边界的应力仍然呈现明显的变化情况。

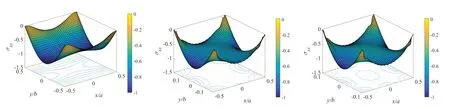
图3 长宽比λ=1，3，5 声子场正应力σxx 的分布Fig.3 Distribution of normal stress σxx in phonon field with aspect ratio λ=1，3，5

4 结论

本文采用微分求积法研究了点群10 mm 十次对称二维准晶的矩形板边缘受余弦分布载荷作用的弹性力学问题。利用微分求积法，将控制方程和应力边界条件转化为代数和方程组，继而求得准晶板位移和应力。之后通过数值算例，得到了以下的结论：

（1）正方形准晶板的位移包括了声子场和相位子场的无穷多个位移函数，并且观察准晶板的位移分布图，声子场和相位子场的位移变化总是关于某一条直线对称。

（2）准晶板声子场和相位子场的应力都呈现明显的非线性分布，并且正应力σxx在受力边界处呈现明显的先增大后减小的趋势，并且在中点处得到最大值。

（3）当边界受非线性分布载荷的作用时，随着准晶板长宽比的不断增大，板内部的应力受外力的影响越来越小，但边界上的应力仍受外力影响，呈现出明显的非线性分布。

图4 长宽比λ=1，3，5 声子场正应力σyy 的分布图Fig.4 Distribution of normal stress σyy in phonon field with aspect ratio λ=1，3，5

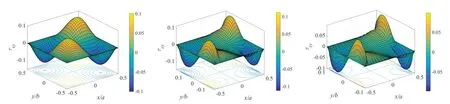
图5 长宽比λ=1，3，5 声子场切应力σxy 的分布图Fig.5 Distribution of shear stress σxy in phonon field with aspect ratio λ=1，3，5

图6 长宽比λ=1，3，5 相位子场正应力Hxx 的分布图Fig.6 Distribution of normal stress Hxx in phonon field with aspect ratio λ=1，3，5

图7 长宽比λ=1，3，5 相位子场正应力Hyy 的分布图Fig.7 Distribution of normal stress Hyy in phonon field with aspect ratio λ=1，3，5

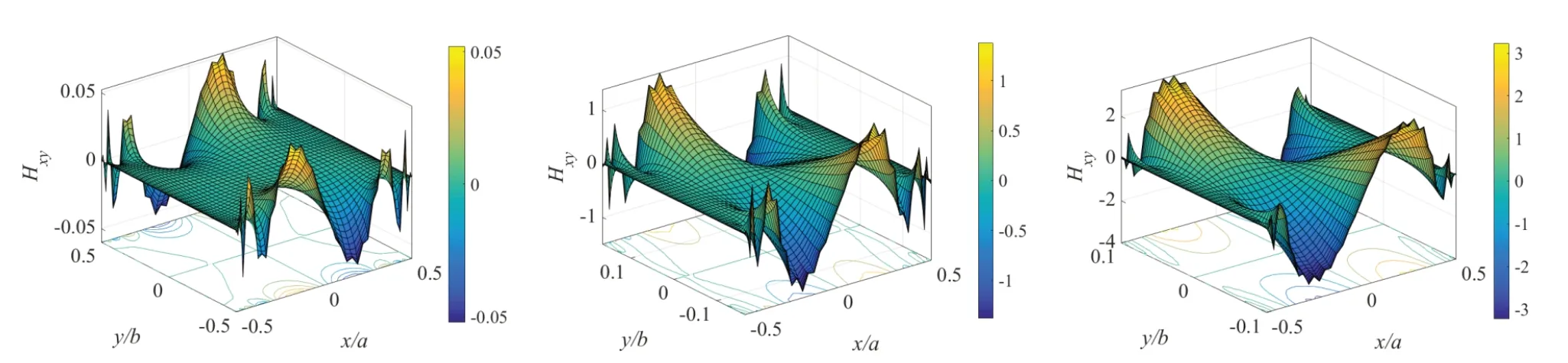
图8 长宽比λ=1，3，5 相位子场切应力Hxy 的分布图Fig.8 Distribution of shear stress Hxy in phonon field with aspect ratio λ=1，3，5

图9 长宽比λ=1，3，5 相位子场切应力Hyx 的分布图Fig.9 Distribution of normal stress Hyx in phonon field with aspect ratio λ=1，3，5