平板静电四极透镜的电场及其数值模拟

王福谦，廖明芳

（1.长治学院 物理系，山西 长治 046011；2.同安中学，四川 成都 610100）

文献[1]对静电透镜的点聚焦特性进行了分析与仿真，文献[2-4]分别用CST、ANSYS 软件和阻尼最小二乘法对静电透镜进行了仿真与优化设计，文献[5-6]分别用改进型的Poweell 为基础的有约束参数方法及龙格-库塔法对静电透镜进行了设计和模拟计算，文献[7]用Lie 代数方法分析了带电粒子在静电四极透镜中的非线性传输，但对静电透镜电场分布定量研究，有关文献还鲜见涉及。为此，文章拟将保角变换法、格林函数法和计算机数值模拟相结合，研究平板静电四极透镜的电场，得到其电势和场强分布函数，利用软件MATLAB 对场分布进行数值模拟，画出其电场线和等势线图，并阐明平板静电四极透镜对电子束的聚焦原理。

1 电势与电场强度

平板静电四极透镜由间距为h、电势分别为U1及U2（U1＜U2）的两组互相平行的极板组成，各平板长度为L1，极板的宽度为L2，且L1＞L2，左、右两组极板的间距为2d，其沿宽度方向的截面如图1 所示。若忽略长度方向的边缘效应，则在垂直于极板长度方向的所有截面上的电场分布都相同，故可取任一截面为z平面来讨论电势和场强在其上的分布（见图1）。因为指数函数可将z平面上 水平带域变换为ζ平面的上半平面，所以，为了利用格林函数法计算z平面上平板静电四极透镜的电势分布，可作如下的保角变换[8]

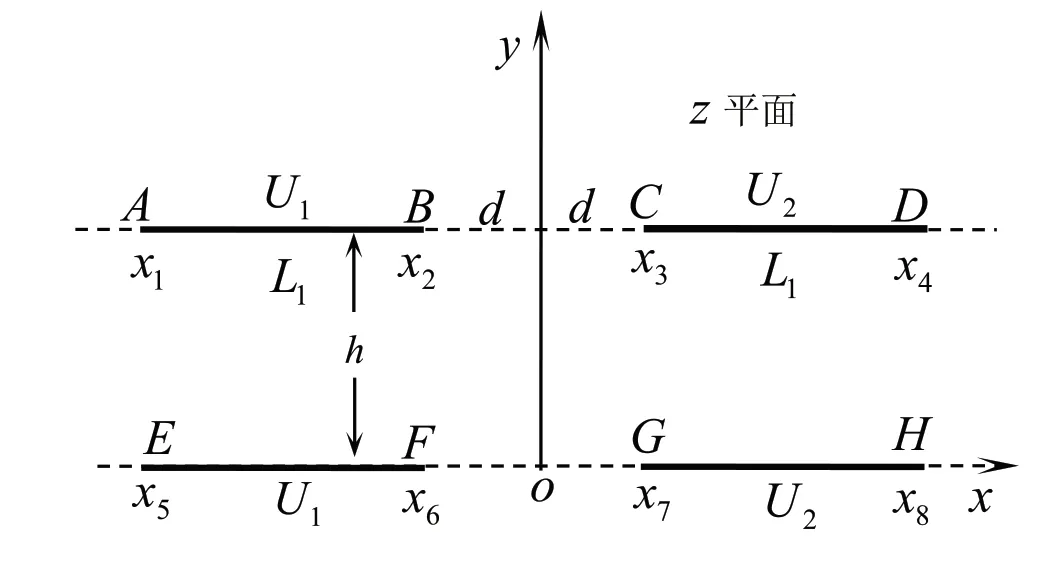
图1 平板静电四极透镜的横截面

经变换式（1），z平面上由平板电极位置所限定的水平带形域 ，就映射为ζ平面的上半平面，变换后的ζ平面上各平板电极横截面的位置及其坐标可由式（1）确定，如图2 所示。

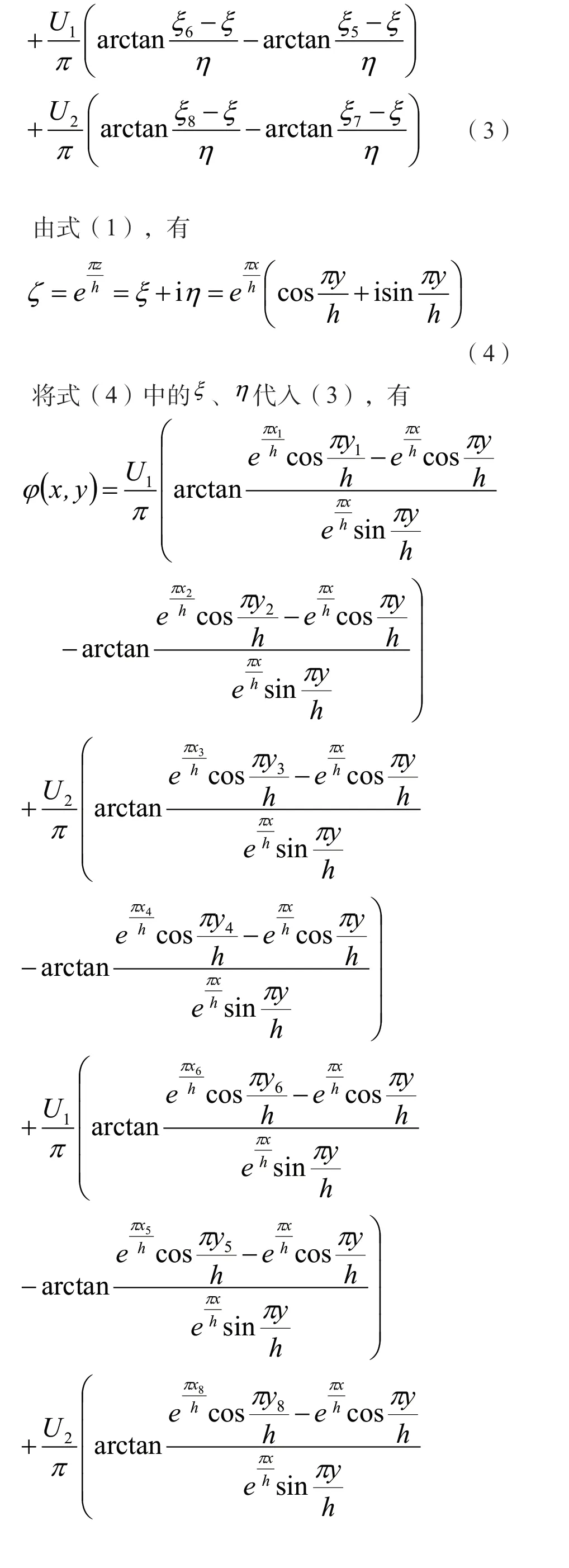
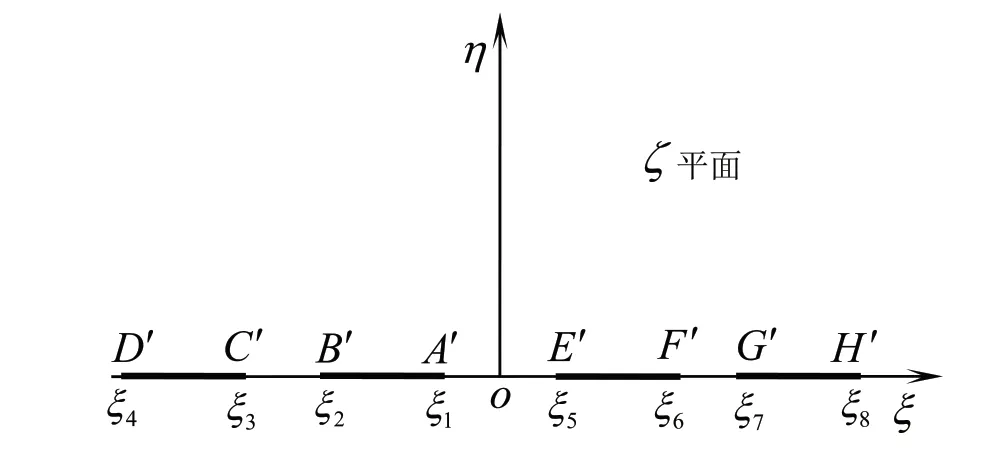
图2 变换后的上半平面

经此变换后，z平面上平板电极间电势分布就变换为ζ平面上的位于其上半平面如下的边值问题对式（2）应用格林函数法[9]，可得ζ平面上的电势分布为

由场强与电势的微分关系E=-φ∇ ，利用式（6）可得

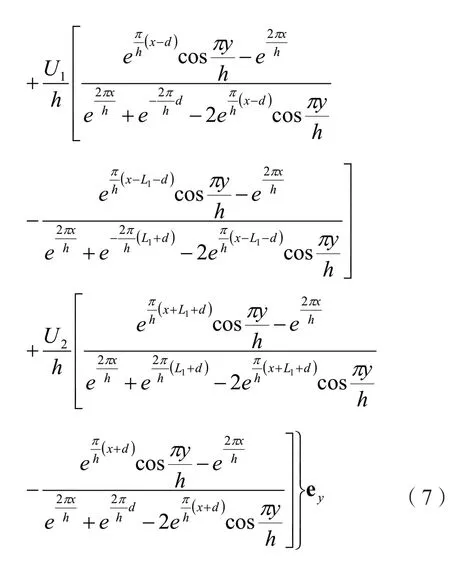
式（7）为平板静电四极透镜电场的场强表达式。

2 电子束静电聚焦原理

2.1 平板静电四极透镜电场分布的数值模拟

为了给出平板静电四极透镜电场分布图的图像，下面用数学软件MATLAB 对该电场分布进行数值模拟[10-11]，其等势线的分布见图3 和图4，其等势面关于零等势面左右对称。

图3 平板静电四极透镜电场的等势面

图3 平板静电四极透镜电场的等势面

2.2 平板静电四极透镜电子束静电聚焦原理

对如图1 所示的平板静电四极透镜的横截面，由式（7）可知，当U1＜U2时，对于x＜0、y＞0区域，有Ey＞0，而对x＜0、y＜0区域，有Ey＜0；对于x＞0、y＞0区域，有Ey＜0，而对x＞0、y＞0区域，有Ey＞0。由透镜左侧的电场分布可知，当电子束水平向右入射时，在透镜的左侧x＜0区域，该透镜对电子束由会聚作用；而又由式（7）可知，当U1＜U2时，对于x＞0、y＞0区域，有Ey＜0，对y＜0区域，有Ey＞0，即当电子束水平向右入射时，在透镜的右侧x＞0区域，该透镜对电子束由发散作用；图3 及图4 中静电透镜的等势面由两电极中心向两侧弯曲，且关于电极中心对称分布，由场强方向垂直于等势面且指向电势降落方向的特点，也能得出与上述讨论相同的场强分布结果。因在图3 及图4 的透镜场强中的场强方向总沿着x轴的负向，电子在透镜中的运动过程是始终在加速，故其在透镜左侧的运动时间长于在右侧的运动时间，静电透镜对电子束的会聚作用大于其发散作用，为会聚透镜。

3 结束语

计算机数值模拟的研究方法已成为继实验研究和理论分析之外的第三种研究手段。文章将保角变换、理论分析与计算机数值模拟相结合，通过保角变换法和格林函数法，研究了平板静电四极透镜的电场，得到其电势和场强分布，利用软件MATLAB 对场分布进行数值模拟，并说明了该透镜对电子束的聚焦原理。文章的研究过程具有物理意义明确、计算方法简便的特点，其研究思路和方法对新型静电透镜的设计和研发具有一定的理论意义和实用价值，也可作为相关问题研究的参考。