异构混合相关熵有源噪声控制算法
2022-11-23李春阳金光灿浩李
李春阳金光灿 刘 浩李 锦
(1上海工程技术大学机械与汽车工程学院 上海201600)
(2上海理想汽车科技有限公司 上海201800)
0 引言
有源噪声控制(Active noise control,ANC)技术由于其优秀的低频降噪能力和被动降噪不具有的小体积、低成本、高灵活性的优势,近几年被广泛应用在耳机、汽车、家电、建筑、医疗等众多领域中[1-2]。在ANC过程中,自适应滤波算法的优劣对系统的降噪能力起到了关键作用。由于结构简单、易于实现的特点,基于最小均方误差准则(Minimum mean square error criterion,MMSE)的滤波-x最小均方(Filtered-x least mean square,FxLMS)算法被广泛应用于高斯噪声的有源降噪过程中[3]。
在实际应用中,脉冲噪声的出现严重降低了ANC算法的降噪能力并影响整个系统的稳定性。为了克服脉冲噪声的不利影响,学者们研究了一系列专门针对脉冲噪声的鲁棒算法[4-6]。其中最典型的算法有基于最小误差p范数的滤波-x最小p阶矩算法(Filtered-x LMP,FxLMP)[7-8],然而该算法需要获取噪声信号的先验信息,这在实际应用中并不容易实现。Wu等[9]利用平方误差的对数矩提出了滤波-x对数最小均方算法(FxlogLMS),该算法虽然避免了参数估计,但算法存在权值更新死区,以至于算法的降噪能力受到限制。为了克服FxlogLMS算法的缺陷,研究者们又分别提出了归一化可切换的对数算法版本(Normalized switch FxlogLMS,NSFxlogLMS)[10]和能作用于非线性脉冲噪声控制的鲁棒滤波-s LMS算法(Robust filtered-s LMS RFsLMS)[11]。
最大相关熵准则(Maximum correntropy criterion,MCC)是来源于信息论(ILT)领域的一种鲁棒优化准则,不同于均方误差(MSE)的全局度量,它表示两个随机变量之间的局部相似性,这对于抑制异常值和脉冲噪声的不利影响十分有效[12],目前相关熵已经被广泛应用在机器学习、信号处理和自适应滤波等领域[13-14],近些年有研究人员将相关熵引入到了ANC的鲁棒控制中[15]。2017年,Kurian等[16]基于MCC准则提出了滤波-s最大相关熵算法(Filtered-s maximum correntropy criterion,FsMCC),该算法在高斯和脉冲环境中都表现出了较好的降噪性能。但是FsMCC算法对核参数十分敏感,导致算法在面对复杂噪声数据时性能明显下降,为了保证降噪性能,一般需要在线更新核宽[15-16]。为了弥补FsMCC算法的不足,2020年,宋普查等[17]通过引入了最大混合相关熵准则(Maximum mixture correntropy criterion,MMCC),提出了滤波-x最大混合相关熵算法(Filtered-x maximum mixture correntropy criterion,FxMMCC)。该算法采用两个不同大小的高斯核组成混合核来替换单一高斯核,仿真表明该算法有更好的降噪性能,但该算法仍面临核宽敏感和强脉冲环境下降噪能力不足的问题。高斯核具有平滑、正定以及极强的逼近能力,因此使用高斯核来抑制异常值是十分合适的,但是高斯核并不一直都是最好的选择。2021年,Ruan等[18]通过理论推导,证明了ℓ1范数的拉普拉斯核相比ℓ2范数的高斯核具有更强的抑制异常值的能力,此外拉普拉斯核对核宽的敏感性显著降低。
考虑到拉普拉斯核具有更出色的抗脉冲能力和更低的核参数敏感度,本文使用高斯核和拉普拉斯核组成异构混合核作为成本函数,推导了基于异构混合核的滤波-x最大相关熵算法(FxMCCmixture kernels,FxMCC-MK)。通过在对称α稳定(Symmetricα-stable,SαS)脉冲噪声环境和真实噪声录声环境下仿真,证明了所提出的算法具有更好的降噪能力。
1 ANC系统模型和相关熵
1.1 ANC系统模型
单通道前馈ANC系统框图如图1所示。ANC系统的工作原理为声波的叠加相消,其中x(n)为靠近噪声端传感器拾取的参考信号,d(n)为需要抵消的初级噪声,P(z)代表主路径系统响应,W(z)是ANC控制器(自适应滤波器),y(n)为控制滤波器输出信号,S(z)代表次路径系统响应,y′(n)为抵消扬声器产生的抵消噪声,e(n)为误差传感器拾取的残余噪声信号代表对S(z)的近似估计。
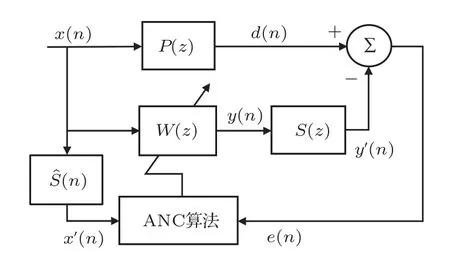
图1 单通道前馈ANC系统框图Fig.1 Single-channel feedforward ANC system block diagram
假设控制滤波器长度为L,则第n时刻输出信号y(n)为
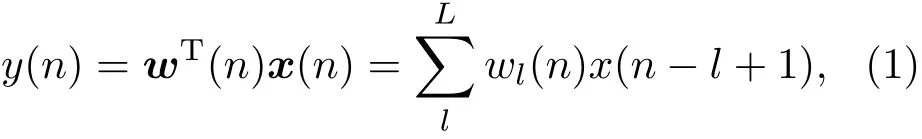
其中,w(n)=[w0(n),w1(n),···,wL-1(n)]T是n时刻控制滤波器的权系数向量,x(n)=[x(n),x(n-1),x(n-L+1)]T是n时刻最近的L个参考信号采样值。
残余误差信号e(n)计算公式为
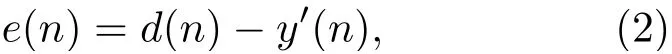
其中,初级噪声d(n)=x(n)*p(n),抵消噪声y′(n)=y(n)*s(n),*代表线性卷积。在实际ANC的实现过程中,e(n)直接通过误差传感器拾取,因此ANC的关键即为采用合适的算法自适应更新滤波器权系数向量w(n)。
1.2 相关熵的定义
相关熵表示任意两个随机变量X和Y之间的相似性,其定义式如下[12,19]:
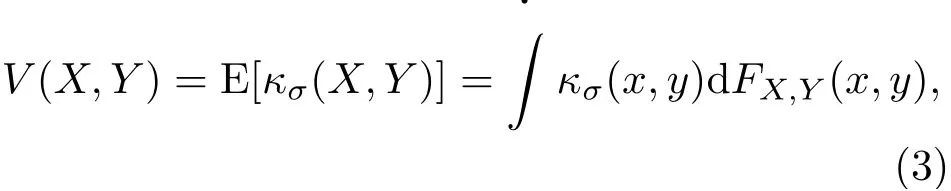
其中,E[·]表示期望运算符;κσ(·,·)表示核宽为σ的Mercer核函数;FX,Y(x,y)表示变量X和Y的联合分布函数。在实际应用中,联合分布函数FX,Y(x,y)是未知的,通常只能获取有限的采样数据因此采用公式(4)来近似估计相关熵:
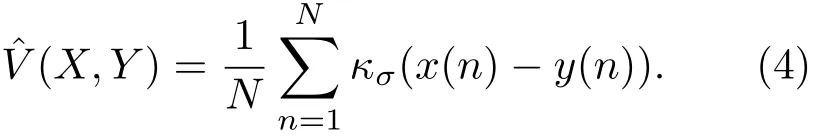
常见的Mercer核是基于ℓ2范数的高斯核函数[16],高斯核函数具有良好的抗干扰能力,但对核宽参数极敏感。而基于ℓ1范数的拉普拉斯核可看作是高斯核的一个变种,它不仅提高了高斯核的抗干扰能力,并且降低了核宽的影响。它们的表达式分别如下:
高斯核:
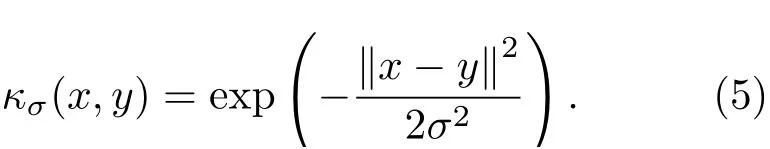
拉普拉斯核:
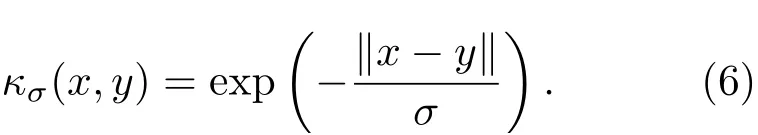
在MCC下,可以通过最大化期望信号和输出信号的相似性来求ANC系统的最优滤波器权向量w,为了便于分析和对比,采用如下求最小值形式来表示ANC系统的代价函数:
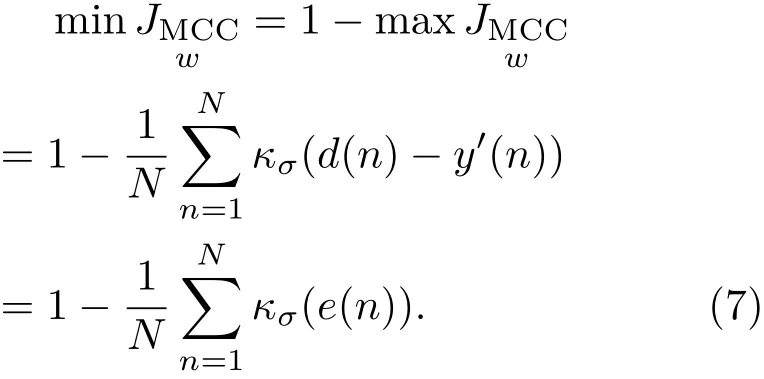
为了比较高斯核与拉普拉斯核,图2绘制了高斯核和拉普拉斯核代价函数的性能表面。其中滤波器权向量简化为二维数据w=[w1,w2],其最优的权向量假设为w0=[10,10];参考噪声信号x(n)使用零均值单位高斯变量。从图2可以看出,在远离最优值时,拉普拉斯核代价函数性能表面平坦,梯度更加平滑,而高斯核则一直持续下降。这种差距意味着在远离最优权向量时,拉普拉斯核有更好的抑制异常值能力,鲁棒性更好。在接近最优滤波器向量时,拉普拉斯核代价函数性能表面是高度非凸的,而高斯核接近最优值时表面为凸且平滑的,这意味着拉普拉斯核在最优解处性能远远不如高斯核,其非凸性甚至会导致陷入局部最优。
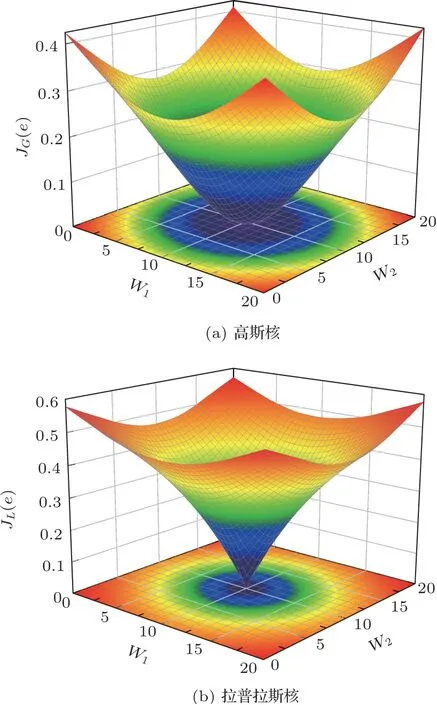
图2 代价函数性能表面Fig.2 Cost function performance surface
2 FxMCC-MK算法
2.1 FxMCC-MK算法代价函数
由第1节的分析可知,高斯核和拉普拉斯核的性能各有优劣。为了更好地增强相关熵算法的降噪能力,本文同时使用高斯核和拉普拉斯核组成混合核,引入异构混合相关熵作为代价函数[13],提出FxMCC-MK算法。
FxMCC-MK算法的代价函数表示为如下形式:
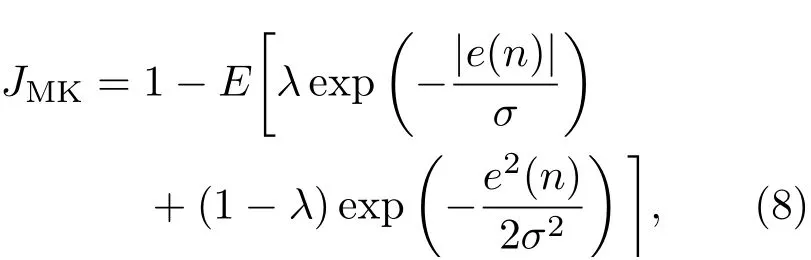
其中,λ是混合系数,λ∈[0,1]。
图3表示不同混合系数下异构混合相关熵的代价函数与误差的变化关系。从图3可以看出,随着混合系数的增加,拉普拉斯核的作用越明显,代价函数曲线在[-2σ,2σ]区间内变化越尖锐,在区间外变化越平缓,这一变化特性对异常离群值有更好的抑制效果。
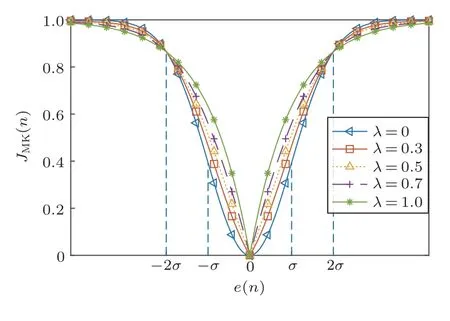
图3 不同混合程度下混合相关熵代价函数Fig.3 Mixture correntropy cost function under different mixing coefficients
2.2 FxMCC-MK算法推导过程
随机梯度是一种简单有效的在线求ANC最优滤波器系数的方法,FxMCC-MK算法代价函数的瞬时梯度向量为
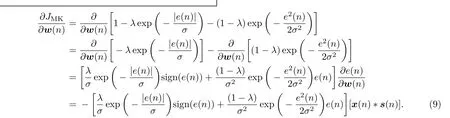
因此所提出的FxMCC-MK算法的权向量更新过程为
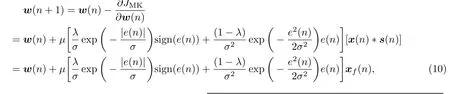
其中,μ表示算法更新步长,σ为核宽参数,λ代表混合参数。
混合参数λ对算法的降噪性能至关重要,由2.1节的分析可知,在出现脉冲噪声时,使用较大的λ能增加拉普拉斯核的比重,从而算法有更强的鲁棒性;在无异常值出现时,更希望用较小的λ来保证算法能找到最优权值。然而在ANC实际的实现过程中,复杂的声环境造成λ无法被准确确定。因此本文继续采用宋普查等[17]的方法,利用等式(11)来自动更新混合参数λ,保证λ随着误差信号的变化自动调整大小。其中,β是形状参数,β≥0。图4为不同β下,混合参数随误差变化曲线。从图4可以看出随着误差的增大,λ(n)逐渐增大,即拉普拉斯核起主要的作用,算法对异常值的抑制能力增强。对于形状参数β的选取规则如下,在强脉冲环境下,其稳态误差e(n)相对较大,此时选用大的β,从而得到较大的λ(n),增强脉冲抗性;在低脉冲条件下,则相反选用小的β值。
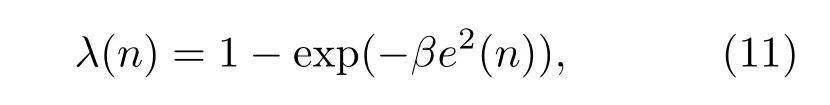
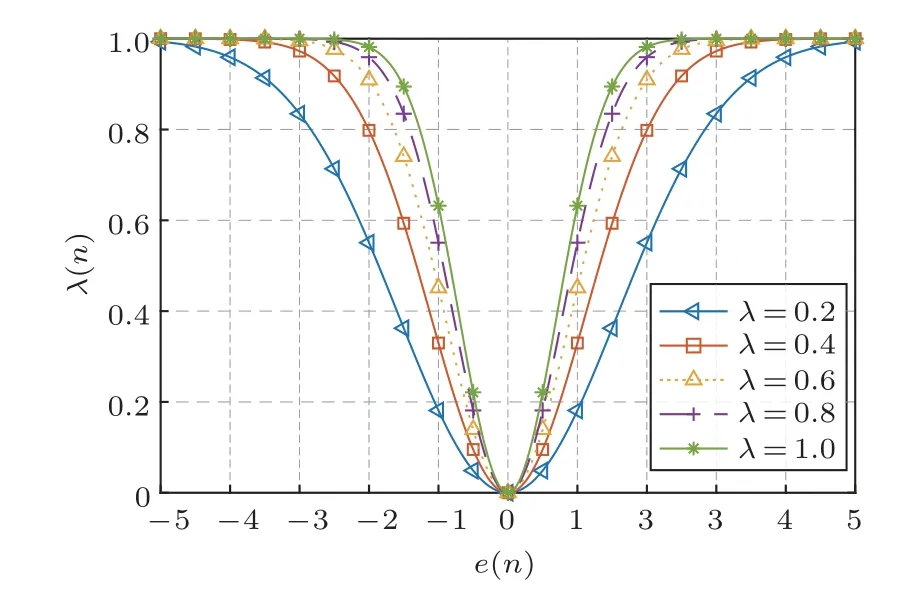
图4 不同β值下混合参数变化曲线Fig.4 Curves of mixed parameter variation under different β values
为了便于阅读,FxMCC-MK算法的伪代码总结在表1。

表1 FxMCC-MK算法伪代码Table 1 Pseudocode of FxMCC-MK algorithm
3 算法分析
3.1 稳定性分析
为了保证算法的收敛和稳态性能,本节主要推导FxMCC-MK算法步长μ的选择范围。假设w0为滤波器的最优权向量,定义误差矢量v(n)=w0-w(n),使用w0同时减去等式(10)两侧可以得到
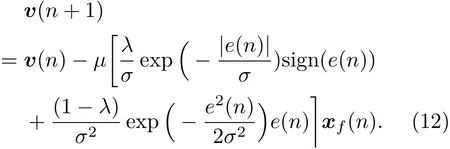
对等式(12)两侧同时求ℓ2范数并取期望,如ϑ(n)=E{‖v(n)‖2},得
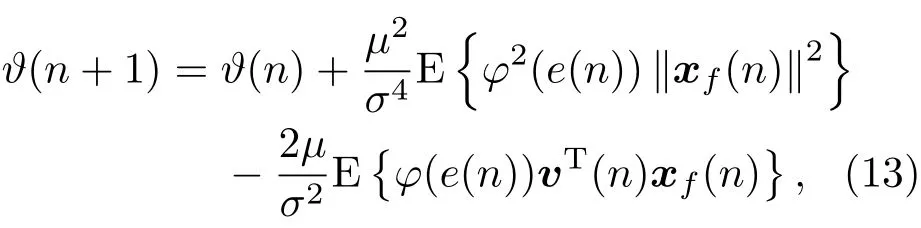
其中,
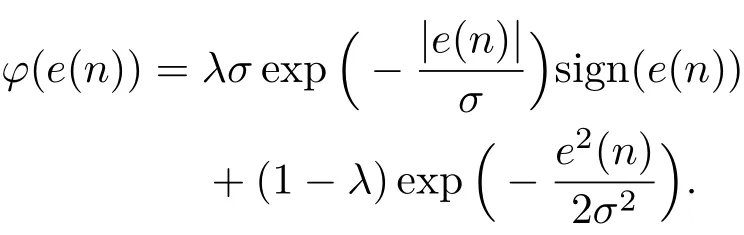
为了保证算法的收敛性,应满足条件ϑ(n+1)<ϑ(n)。假设vT(n)xf(n)=(w0-w(n))Txf(n)≈e(n),因此可以推导出FxMCC-MK算法步长μ的选择范围为
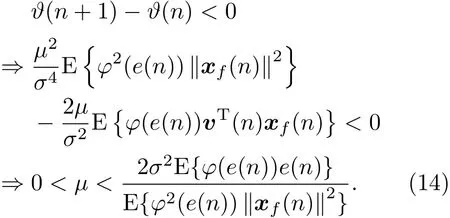
3.2 计算复杂度对比
在ANC的实际应用中,为了保证算法实时运算并降低硬件系统的负担,ANC算法应当简单有效。本文提出的算法与已有的算法计算复杂度对比如表2所示。其中L表示控制滤波器抽头系数的个数,M表示用来估计次级路径模型的滤波器长度。从表2可以看出,相比于经典的FxLMS算法,本文提出的算法只略微增加了计算量,为了获得更好的鲁棒性能,增加的这些额外计算负担是完全可接受的。

表2 算法计算复杂度Table 2 Computational complexity of the algorithms
4 计算机仿真
为了展示算法的降噪性能,将提出的算法与已有的算法在计算机仿真环境中对比。其中,初级路径系统函数P(z)和次级路径系统函数S(z)分别设置为
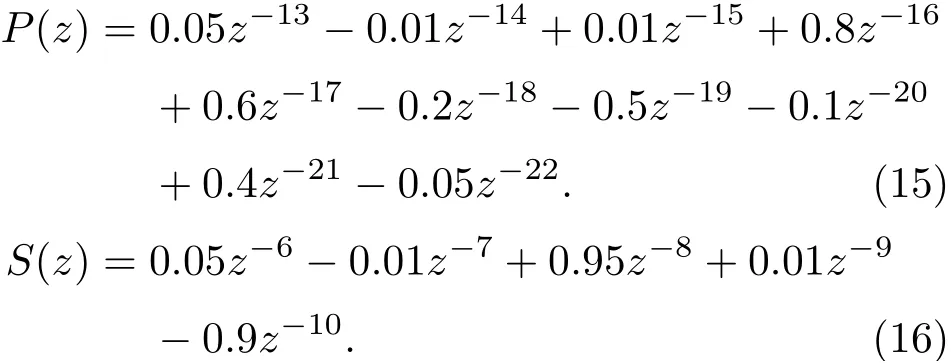
控制滤波器使用20阶有限冲激响应(Finite impulse response,FIR)滤波器进行建模。
仿真中使用的脉冲噪声服从标准SαS分布其特征函数为
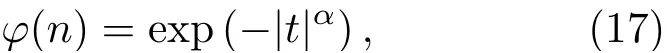
其中,α是特征指数,α值越小,表明异常值出现的可能性越大。生成的SαS脉冲噪声信号的时域分布如图5所示。
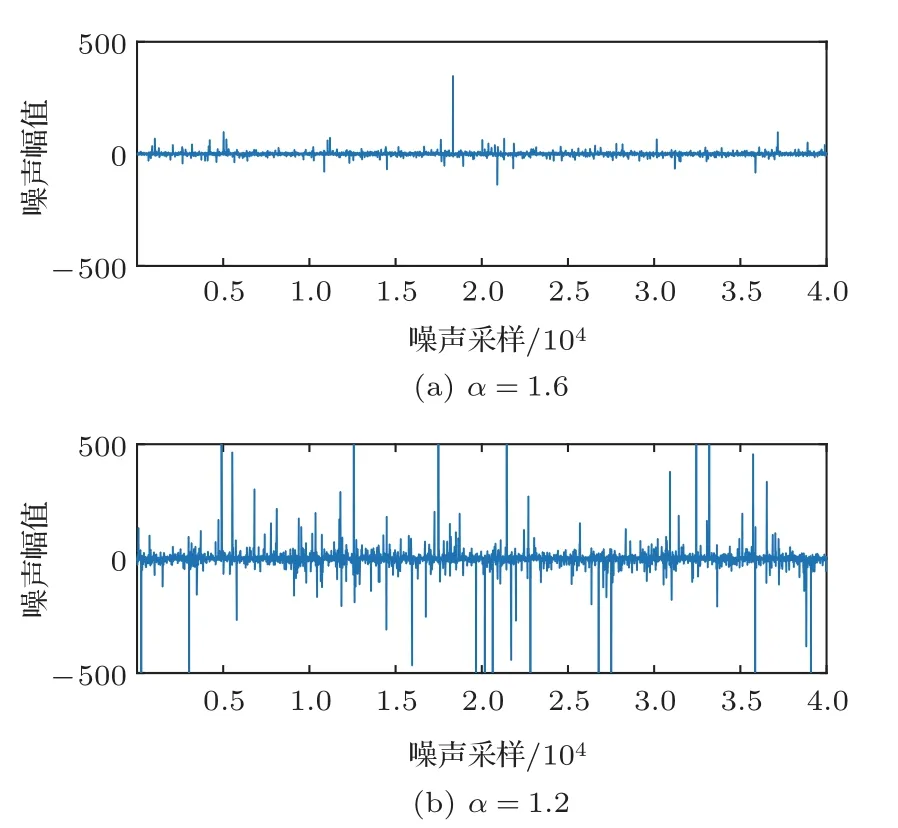
图5 SαS脉冲噪声时域分布图Fig.5 Time domain distribution of SαS pulse noise
使用平均噪声衰减量(Averaged noise reduction,ANR)来评估算法降噪性能的优劣,ANR的定义公式如下[20]:
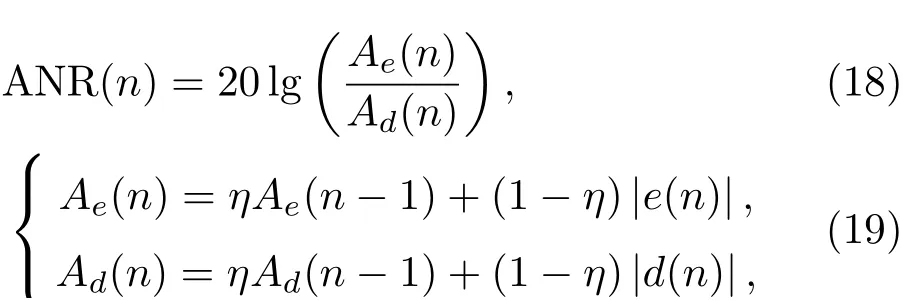
其中,η是遗忘因子,η=0.999;Ae和Ad的初始值为0。
为了更好地比较各算法的降噪性能,本文的仿真结果均是在算法独立运行100次后取平均值获得的。
4.1 核宽σ对算法性能影响
在本例中,主要对比提出的FxMCC-MK算法和已有的FxMCC算法对核宽参数σ的敏感度差异,并研究参数σ对FxMCC-MK算法降噪性能的影响。其中输入参考噪声为α=1.6的SαS合成脉冲信号,每次采样点数为4×104,核宽σ值依次设置为3、7、15、20、30,FxMCC算法的步长为μ=0.0005,FxMCCMK算法的步长为μ=0.0009。两种算法的降噪性能曲线如图6所示,其中横坐标代表迭代次数,纵坐标为ANR。降噪算法的评价指标一般有收敛速度和稳态失调量,在图6中表现为曲线斜率越大,算法收敛速度越快;收敛后ANR值越低,即稳态失调越小,降噪能力越强。
从图6(a)可以明显看出,取用不同σ值,FxMCC算法的稳态性能差距很大,其中σ=3时稳态ANR为-35 dB;在σ=30时,ANR稳定在-25 dB左右,稳态ANR差距越为10 dB。然而在图6(b)中,σ值变化对FxMCC-MK算法稳态性能几乎没有影响,σ在3~30取值时,其稳态ANR基本都保持在-35 dB左右,上下浮动小于0.5 dB。以上结果表明,FxMCC-MK算法对核宽σ的依赖性降低,这意味着算法在面对复杂的声环境时能降低核宽对性能的影响,从而算法具有更好的适应性。
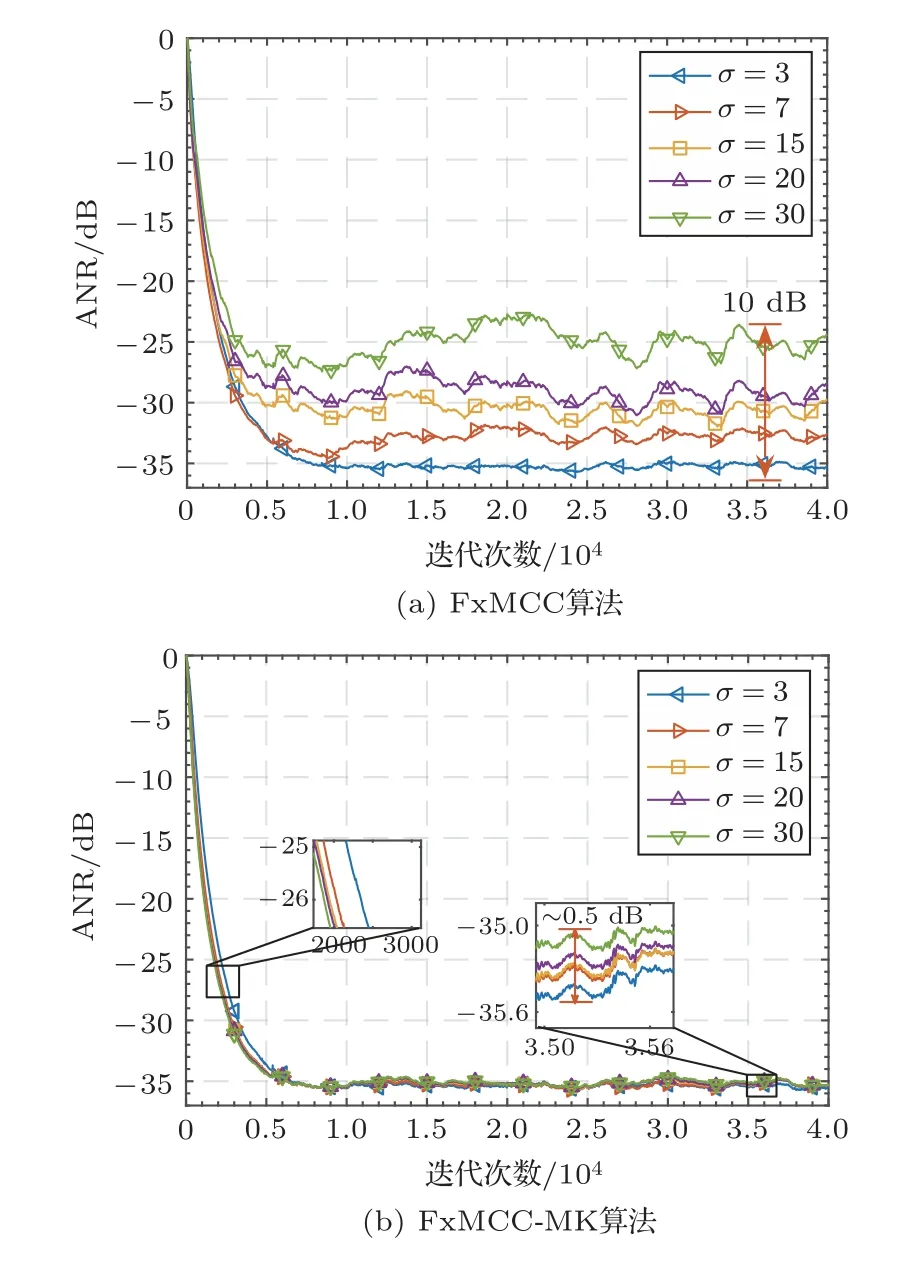
图6 核宽σ对算法性能影响曲线Fig.6 The influence curve of kernel width σ on algorithm performance
从图6(b)可以看出,σ值的变化对FxMCCMK算法的性能仍有一定的影响,在σ从3递增到30的过程中,算法的收敛速度逐渐加快,稳态ANR值也会略微升高。以上结果表明,较大的σ值可以获得更快的算法收敛速度但会降低算法的鲁棒性,较小的σ值情况则完全相反,这一变化特性与FxMCC算法相似。
4.2 SαS强脉冲噪声环境下降噪性能对比
在本节仿真实验中,主要验证在α=1.2的SαS强脉冲噪声环境下所提算法的降噪性能。将本文提出的算法与已有的FxMCC算法[16]和FxMMCC算法[17]对比,并引入标准的FxLMS算法作为参考。和4.1节一样,同样采用ANR曲线评价各算法的表现性能。从4.1节的仿真可知,在SαS噪声环境下,当σ=7时,FxMCC算法和FxMCC-MK算法均能取得一个较好的降噪表现,因此在本节仿真中,将FxMCC算法和提出的FxMCC-MK算法的核宽σ均设置为7,FxMMCC算法核宽设置为σ1=5、σ2=7。各算法的其余参数设置如表3所示。为了更好比较强脉冲噪声环境下各算法的降噪性能,除FxLMS算法外,其余的3种鲁棒算法是在相近的收敛速度前提下,比较稳态ANR值。稳态ANR值越低,表明该算法的降噪性能越强。

表3 各算法仿真参数Table 3 Simulation parameters of each algorithm
图7是α=1.2时各算法平均噪声衰减对比曲线。从图7可以看出,在α=1.2的强脉冲环境下,非鲁棒的FxLMS算法直接失效;其余算法中提出的FxMCC-MK算法表现最好,最终ANR值为-28 dB,比FxMCC算法的-23 dB提升约5 dB,比FxMMCC算法的-25 dB提升约3 dB。以上结果表明,提出的FxMCC-MK算法在强脉冲环境下,相比已有算法具有更好的鲁棒性,算法能取得更好的降噪效果。
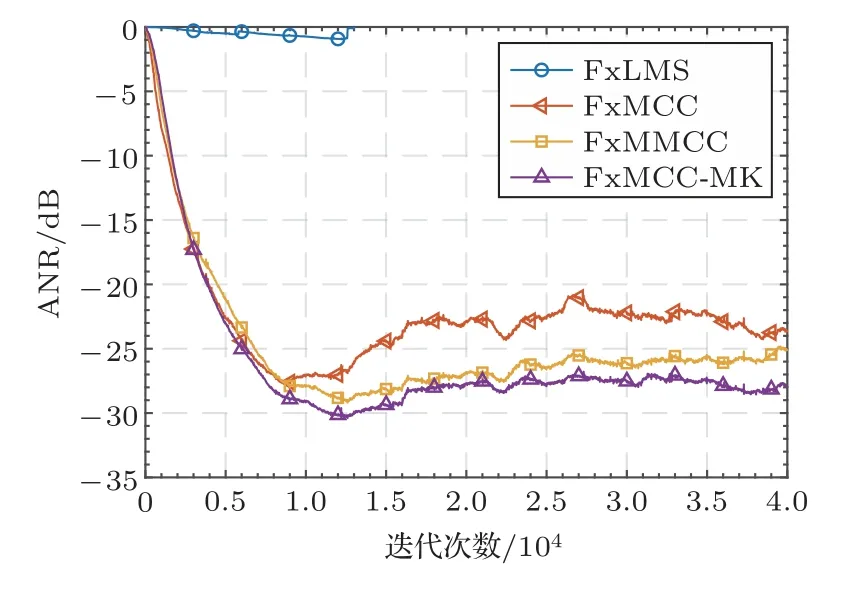
图7 α=1.2时各算法平均噪声衰减曲线Fig.7 Average noise reduction curves of each algorithm(α=1.2)
4.3 真实噪声环境下降噪性能对比
本节使用实验室测得的管道中声音传播路径和录制的冲压机噪声进行算法降噪效果对比验证。初级路径P(z)和次级路径S(z)的单位脉冲响应如图8所示。控制滤波器使用256抽头的FIR滤波器进行建模。FxMCC算法和FxMCC-MK算法的核宽σ设置为0.1,FxMMCC算法核宽设置为σ1=0.15、σ2=0.05,其余参数被设置在表3中。
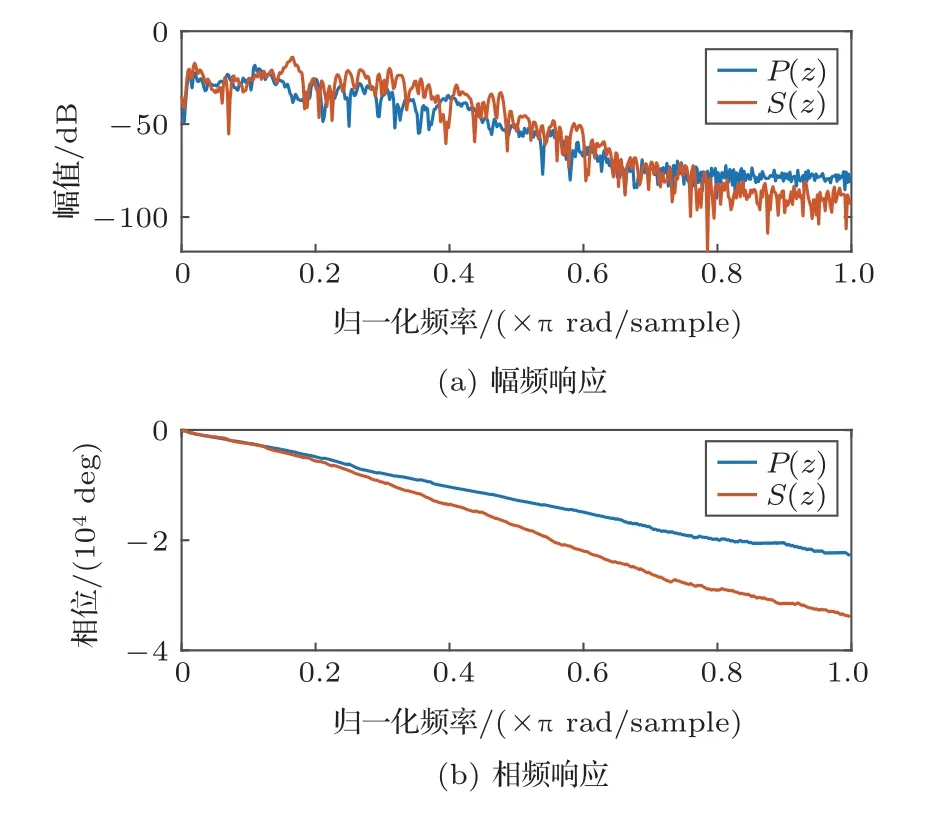
图8 P(z)和S(z)幅频响应和相频响应Fig.8 The frequency response of P(z)and S(z)
图9为冲压机噪声环境下各算法的ANC性能曲线。从图9可以看出,4种算法以相近的收敛速度趋向收敛,随着脉冲噪声的出现,ANR曲线均出现较大波动。其中FxLMS算法表现最差,最终平均噪声衰减量为-14 dB。本文算法在3×104次迭代后,算法趋向收敛,最终平均噪声衰减为-29 dB,相比于FxMCC算法的-24 dB降低了约5 dB,相比于FxMCC算法的-26 dB降低了约3 dB,本文算法的最终降噪效果如图10所示。可见,本文的算法在处理真实脉冲噪声时同样具有更小的稳态误差,算法展示出了更好的降噪性能。此外,在ANC的实际实现过程中,声音的传播路径和噪声的特性可能随时发生变化,FxMCC算法和FxMMCC算法需要十分合适的参数设置才能取得较好的降噪效果,而提出的算法则对参数不那么敏感,在实际降噪中可能差距会更明显。
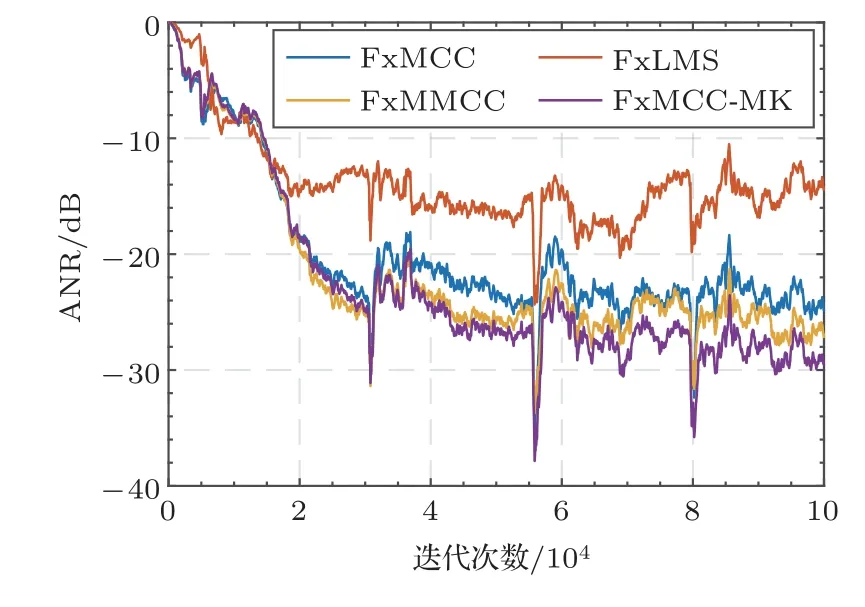
图9 冲压机噪声环境下各算法平均噪声衰减曲线Fig.9 Average noise reduction curves of each algorithm under punch press noise
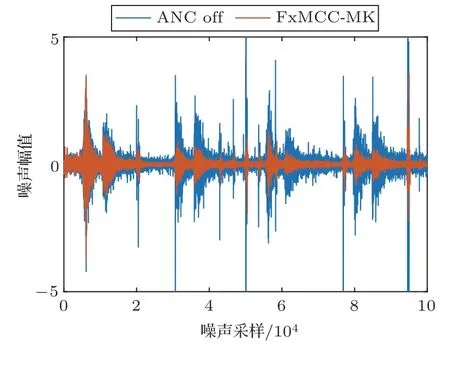
图10 FxMCC-MK算法对噪声有源控制结果Fig.10 Result of FxMCC-MK algorithm for ANC
5 结论
本文针对脉冲噪声的主动控制问题,采用异构混合相关熵作为代价函数,推导了FxMCC-MK算法;并给出了算法的稳定收敛条件和计算复杂度;本文通过理论分析和仿真验证都表明了所提算法具有更好的降噪性能。
本文提出的异构混合核FxMCC-MK算法改进了已有高斯核算法的不足,通过混合参数的自动调节,使算法同时具有高斯核和拉普拉斯核的优势,降低了算法对核参数的依赖性,使算法在复杂声环境下具有更好的适应性;同时增强了算法在强脉冲环境下的鲁棒性。仿真结果表明,在SαS脉冲噪声环境和真实噪声录声仿真中,提出的算法都具有更好的降噪性能。
