应用于助听器反馈抑制的信噪比自适应滤波算法*

陆悠南崔 杰 肖 灵

(1中国科学院声学研究所 北京100190)

(2中国科学院大学电子电气与通信工程学院 北京100049)

0 引言

对于大多数配戴助听器满意度不高的听障患者，啸叫现象是最主要的原因之一[1]。啸叫是声反馈达到一定条件时引起的刺耳声音，它不仅影响助听器的音质和佩戴舒适度，更限制了助听器的有效增益。因此如何抑制声反馈，提高助听器的有效增益是当前助听器设计所面临的关键问题。啸叫形成需要同时满足两个条件，第一个是增益条件，反馈路径和前向路径的增益乘积大于1；第二个是相位条件，两个路径的相位满足相差2π的倍数。

针对啸叫的问题，很多学者进行了研究。Patronis[2]提出了自动增益降低法，当检测到啸叫即将产生时，降低前向路径的全频带增益，从而快速抑制啸叫，抑制方法简单且有效，但忽略了降低增益会限制佩戴者的听觉效果这一问题。Schroeder[3]提出了基于频移来进行声反馈抑制，通过移动频率来平滑闭环系统的增益频谱，信号在同频率处的幅度值不会循环叠加，从而破坏声反馈形成的条件，但是对输入信号移频易造成失真现象，对信号的音质损伤较大，具有一定的局限性。基于陷波器的啸叫抑制法采用陷波滤波器对发生啸叫的频率段进行滤波，从而抑制啸叫，在啸叫频率检测点准确的情况下对输入信号其他频率的影响很小，一般与其他方法结合使用[4]。基于自适应滤波器的声反馈方法可以动态地估计声反馈路径，产生一个声反馈的估计信号来抵消声反馈信号，实时地抑制声反馈形成的条件，从而达到抑制反馈、提升系统增益的效果。助听器体积和功耗的特殊性，使得它无法使用复杂度很高的自适应算法且对自适应滤波器的阶数有限制，因此以最小均方(Least mean square,LMS)为基础的自适应滤波算法为助听器反馈抑制领域的研究重点。Kates[5]提出了LMS算法更新自适应滤波器模拟反馈路径，通过断开前向路径，在验配阶段输入白噪声更新静态滤波器，将静态滤波器与动态滤波器结合，从而达到反馈抑制的效果。LMS算法步长固定，在实际使用中虽然简单且易于实现，但不能同时获得较快的收敛速度和良好的稳定性能。Slock验证了归一化最小均方(Normalized least mean square,NLMS)算法对输入信号为语声信号时相比LMS算法有更好的收敛性能[6]。LMS和NLMS算法因其简单高效，被广泛应用于信号处理领域，同时基于LMS和NLMS的优化也有很多优秀的研究成果[7-14]。针对脉冲响应稀疏性的特点，Duttweiler[9]提出了系数成比例的NLMS算法，即PNLMS算法，通过比例分配滤波器的权值增量，从而提升算法的收敛速度。Khoubrouy[15]将一种无延时的子带滤波技术应用在数字助听器声反馈消除中，使滤波器每个频带独立，解决了数据路径延迟和信号失真的问题。

在电话系统中同样存在回声消除的问题，其对回声的延时要求限制于150 ms，远远大于助听器的10 ms限制要求，因此电话系统的回声语声信号的相关性远远弱于助听器，这就使电话系统与助听器的回声消除算法存在一定区别。同时由于电话系统的长回声路径，滤波器建模需要较高的阶数，计算复杂度也就越大[16-17]，而助听器体积小功耗小，无法使用复杂度高的算法，这也是电话系统回声消除算法无法直接应用于助听器的原因。由于助听器传声器与受话器的距离较小，语声信号具由较强的相关性，在收敛过程中会加大失调量，依然存在收敛速度与失调量的折衷问题。本文针对数字助听器的反馈抑制中语声的相关性问题，提出了一种基于信噪比的自适应滤波算法以解决强语声相关性引起的失调量增大问题。

1 自适应滤波反馈抑制系统

自适应滤波助听器反馈抑制系统框图如图1所示，系统主要由反馈路径、前向路径及自适应滤波模拟反馈路径3部分构成。

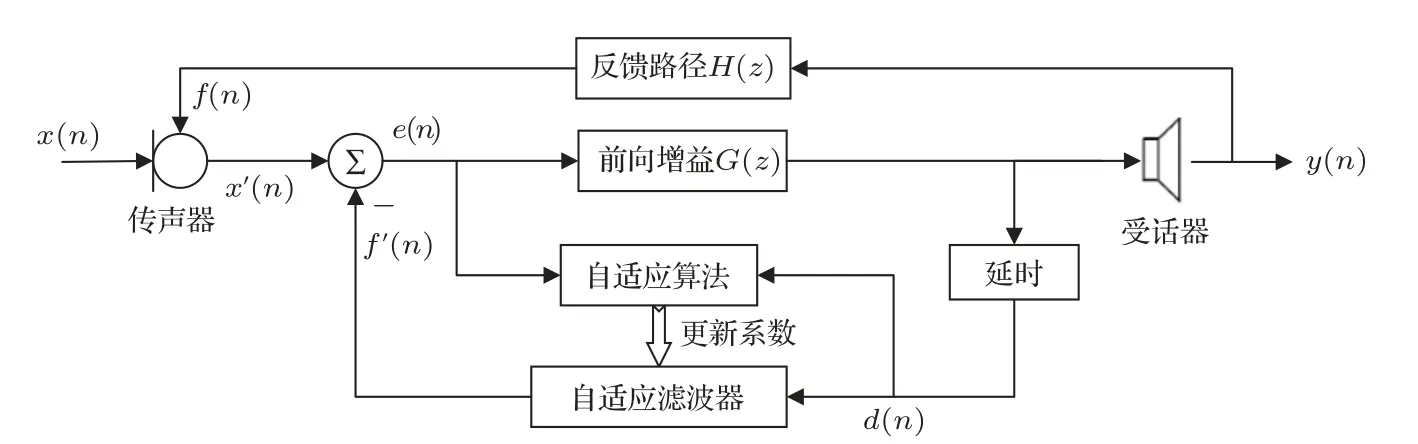
图1 自适应滤波助听器反馈抑制系统框图Fig.1 Block diagram of feedback cancellation system in hearing aids based on adaptive filter

传声器实际输入信号x′(n)由环境输入信号x(n)和反馈信号f(n)叠加组成，

其中，反馈信号f(n)由受话器输出信号y(n)经反馈路径H(z)产生，则f(n)=h(n)*y(n)，*表示卷积，h(n)表示H(z)的单位脉冲响。自适应滤波器的输出为模拟反馈信号f′(n)，

其中，w(n)为自适应滤波器的系数向量，w(n)=[w0(n),w1(n),K,w(n)L-1]T，L为滤波器的长度。自适应滤波器系数w(n)由延时后的受话器输出信号d(n)和误差信号e(n)自适应更新。传声器接收到的信号是环境输入信号和反馈信号混合而成，误差信号e(n)表示为传声器实际输入信号与模拟反馈信号的差，

等同于e(n)=x(n)+f(n)-f′(n)，即反馈路径与模拟反馈路径的误差信号与语声输入信号的和，因此自适应滤波器的性能决定了反馈抑制系统的性能。受话器实际输出信号y(n)为反馈抑制后的信号e(n)经前向路径G(z)后的增益放大信号，

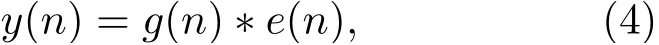
其中，g(n)为G(z)的时域表现形式。定义系统函数为C(z)，

2 自适应滤波算法

2.1 NLMS算法原理

NLMS对于输入矢量的平方欧式范数进行归一化，从而相对于LMS算法获得更快的收敛速度和更好的稳定性能[18]，其更新公式如下：

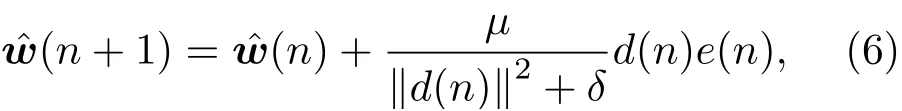
于是，从w中减去式(6)的等式两端，则可得到

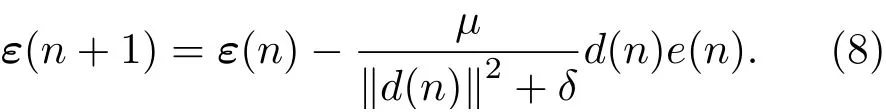
假设n时刻达到滤波器收敛的最优状态，则ε(n)为最小值εmin，则式(8)可转换为

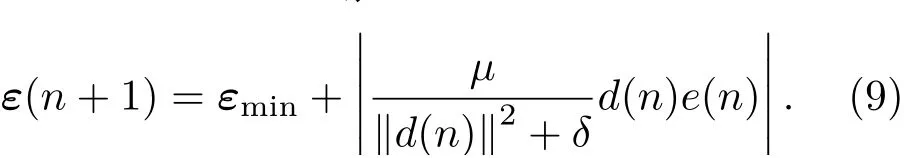
由式(9)可明显看出，当步长μ值越大的时候，滤波器稳态时的失调也随之越大。当d(n)e(n)之间的相关性增加时随之增大，同时滤波器稳态时的失调也越大。在助听器的反馈抑制中NLMS算法相较于LMS算法虽具有良好的收敛性能，但由于助听器的反馈信号与输入语声信号具有极大的相关性，依然存在稳态失调受语声相关性影响增大的问题。

2.2 基于信噪比的步长控制

随着助听器技术的发展，助听器的体积越来越小，传声器和受话器的距离越发靠近，随之而来的是语声信号的相关性越来越强。当语声信号相关性越强时，滤波器的误差则越大且稳态失调量也随之越大。为了解决语声信号相关性带来的失调量增大问题，本文引入信噪比控制步长，优化自适应系统的性能，从而提高反馈抑制系统的有效增益。由于纯净语声的相关性更强，当纯净语声占信号的主要部分即信噪比越高时，自适应滤波器的更新误差增大，因此需要在信噪比高的情况下，限制自适应算法的步长，减缓自适应滤波器的收敛速度，从而减小更新误差。同理，在信噪比越低的情况下，噪声占信号的主要部分，由于噪声的相关性较小，因此增加算法步长，加快自适应滤波器的收敛速度。

基于信噪比的NLMS算法框图如图2所示，采用最小值统计法估计出误差信号的噪声能量，从而估计误差信号e(n)的信噪比控制NLMS算法中的步长μ，关系可表示为式(10)：

图2 基于信噪比的NLMS算法框图Fig.2 Block diagram of NLMS algorithm on SNR

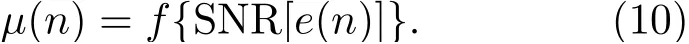
要估计误差信号的信噪比，需要先估计出误差信号的噪声能量，本文采用最小值统计法估计噪声能量，最小值统计法是Martin[19]基于含噪语声功率谱密度的最小统计和最优平滑理论提出的，通过跟踪带噪信号能量的最小值估计噪声能量，其实现步骤如下：

先对带噪语声e(n)进行希尔伯特变换，求得带噪语声的能量，假设为Y(n)。对Y(n)进行平滑得到平滑能量P(n)，P(n)的计算采用一阶递归的形式，即

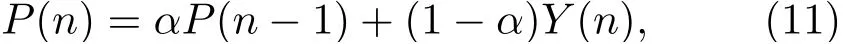
其中，P(n-1)为上一时刻的平滑能量，α为平滑参数，0＜α＜1。然后，在长度为D的窗内搜索最小能量，设置临时变量Ptemp，Ptemp(1)=Y(1)。如果当前时刻可被D整除，则能量最小值Pmin、Ptmp分别依照式(12)和式(13)更新：

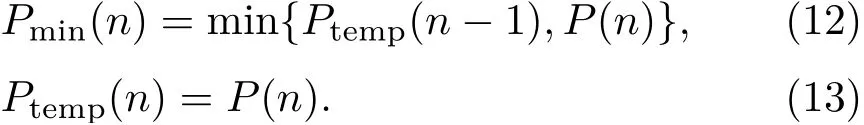
如果不可被D整除，则Pmin、Ptemp分别依照式(14)和式(15)更新：

因为在估计噪声能量中取的是能量的最小值，所以需要对噪声能量进行偏差补偿，补偿因子设为omin，由式(16)可得估计的噪声能量

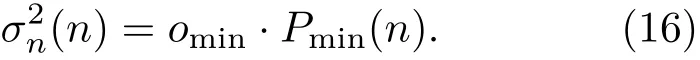
由计算得到的含噪语声能量Y(n)和噪声能量可计算得纯净语声信号能量那么依式(17)可计算得信噪比：

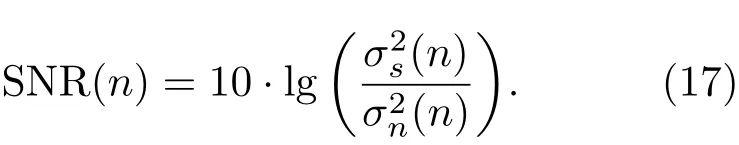
根据计算得到的输入信号信噪比，由式(18)的步长与信噪比的对应关系计算出自适应算法的步长。当输入信号信噪比越高时，语声成分在信号中占比越大，由于语声信号的强相关性会增加自适应滤波器的更新误差，因此使更新步长越小；当信噪比超过最大值SNRmax时，步长固定为步长最小值μmin。同理，当输入信号信噪比越低时，噪声成分在信号中占比越大，噪声信号具有弱相关性，不会增加自适应滤波器的更新误差，因此使更新步长越大，加快自适应算法的收敛速度；当信噪比小于最小值SNRmin时，步长固定为步长最大值μmax。

其中，β和η由当信噪比等于SNRmax时步长为μmin和当信噪比等于SNRmin时步长为μmax的两组数据代入求得，即解式(19)可得：

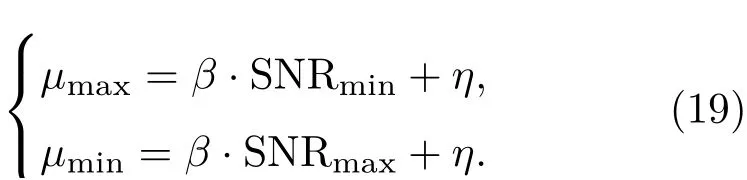
2.3 计算复杂度分析

在实际助听器应用过程中，系统的降噪模块包含信噪比估计部分，因此在实际应用过程中，可以借助降噪模块计算得到的信噪比来避免信噪比估计所产生的计算复杂度，因此在计算基于信噪比的NLMS算法的复杂度过程中忽略了信噪比估计过程的复杂度。

一帧信号的长度为N，自适应滤波器长度为M，按照文献[20]的计算复杂度的方法将分为4个部分，则算法的计算复杂度如下：

(1)信噪比步长更新，乘法次数为N/N；

(2)计算‖d(n)‖2，乘法次数为N/N；

(3)经过自适应滤波器计算模拟反馈信号，乘法次数为M×N/N；

(4)计算自适应滤波器系数，乘法次数为(M×N+N)/N。

因此，综上所述基于信噪比的NLMS算法的计算复杂度约为2M+3，比NLMS算法的计算复杂度略高一点，但在反馈抑制性能方面具有更好的效果，LMS算法、NLMS算法、PNLMS算法及相关复杂度如表1所示。

表1 算法复杂度对比Table 1 Algorithm complexity comparison

3 仿真实验及结果分析

3.1 实验条件

对提出的基于信噪比的自适应算法进行仿真实验，并且对比不同类型算法验证算法的性能。仿真实验给出一个反馈路径滤波器，记为f，其阶数为120，其单位脉冲响应如图3所示。

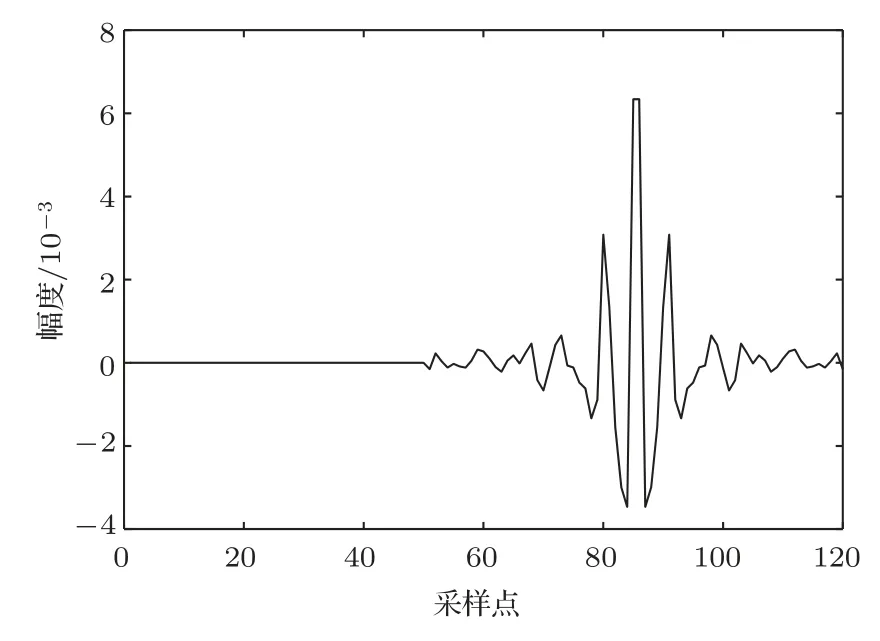
图3 反馈路径的脉冲响应Fig.3 Impulse response of the feedback path

为了验证算法的反馈抑制性能，采用语声信号作为输入信号，采样频率为16 kHz，如图4所示。

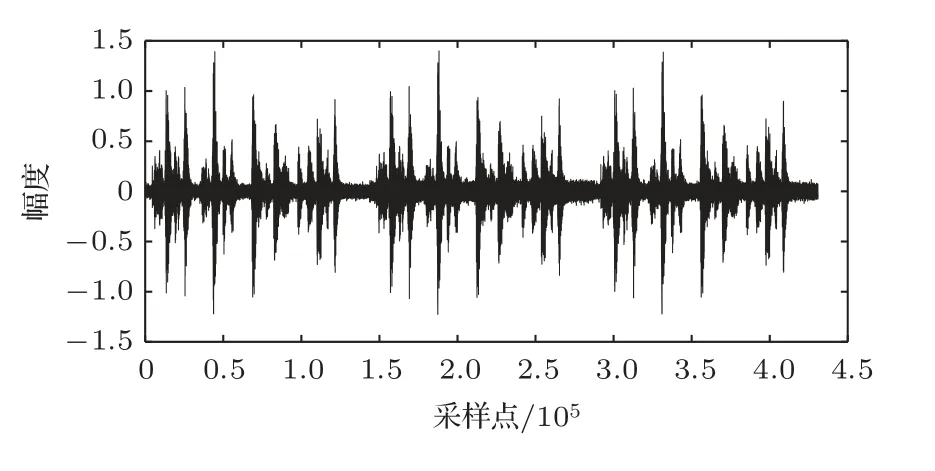
图4 语声信号Fig.4 Voice signal

3.2 实验结果分析

3.2.1 噪声估计结果

首先测试噪声估计的性能，对输入语声信号分别加入1 dB和10 dB的白噪声测试噪声估计性能，如图5所示，估计的噪声能量与实际噪声能量曲线基本吻合，由于通过信噪比来控制自适应算法的步长，在有语声输入时存在的细微误差，在计算信噪比和步长过程中可忽略不计。

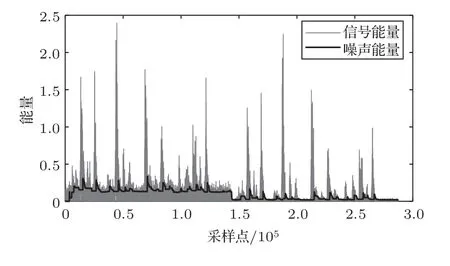
图5 噪声能量估计Fig.5 Noise energy estimation

3.2.2 自适应算法性能分析

为了评估自适应算法的性能，使用自适应滤波法的失调量(Misalignment,MIS)作为算法的性能指标[21]。其表达式为

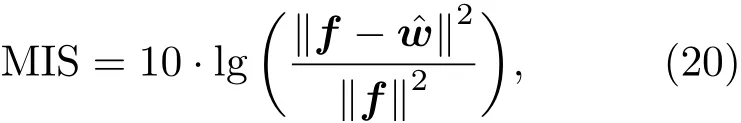
其中，f和ˆw分别为仿真反馈路径和自适应滤波器脉冲响应的权值向量。当失调量的值下降得越快说明收敛速度越快，就能越快地估计出反馈路径。当稳态的失调量越小，说明稳态失调越小，估计的反馈路径越逼近真实值。

在本次实验中，在不同增益的情况下对比了LMS算法、NLMS算法、PNLMS算法[9]及基于信噪比的NLMS算法，4种算法的参数取相近收敛速度的情况下观测系统的失调性能，算法的复杂度由小到大按顺序分别为LMS算法、NLMS算法、基于信噪比的NLMS算法、PNLMS算法。4种算法的步长更新公式及参数取值如表2所示。

表2 算法参数Table 2 Algorithm parameters

取表1参数值，当增益为36.9 dB时，不同算法的失调量如图6所示。

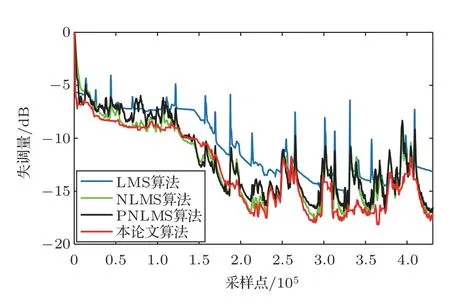
图6 不同算法的失调量Fig.6 Normalized maladjustment of different algorithms

在同一种自适应滤波算法中，步长越大，收敛速度越快，与之同时失调量则越大。如图6所示，可明显看出算法收敛速度由慢至快的顺序为NLMS、PNLMS、LMS、基于信噪比的NLMS算法。图7为4种算法在稳态范围的失调量，可明显看出基于信噪比的NLMS算法的稳态失调量具有一定的优势，不仅具有更低的平均稳态失调量，同时稳态失调量的动态范围也更小。同时，本文提出的算法更多的是对有语声信号时的失调量起伏范围具有参考意义，在信噪比低的时候其性能是和NLMS算法接近的，而在信噪比高的时候，观察图6可明显发现其他算法在语声出现时都会出现高的失调量，而本文算法在语声出现时减小了语声相关性引起的失调量增大问题，提升了算法的性能。

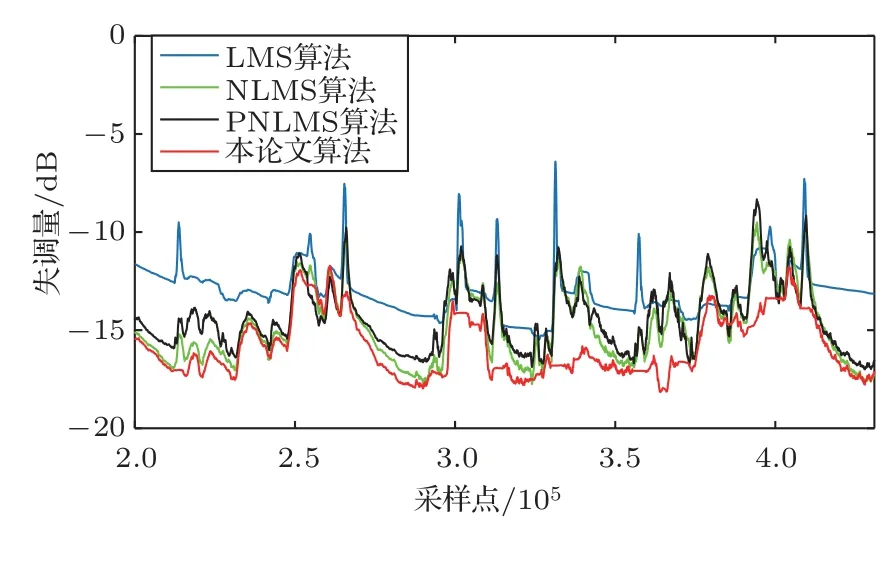
图7 不同算法的稳态失调量Fig.7 Steady-state maladjustment of different algorithms

根据图6可得到达稳态的收敛速度由快至慢的算法分别为基于信噪比的NLMS算法、LMS算法、PNLMS算法和NLMS算法，并可明显得出基于信噪比的NLMS算法的收敛速度具有明显的优势，能够更快地到达稳态阶段，当助听器使用者佩戴助听器的佩戴条件发生改变时，滤波器重新开始收敛。当算法收敛速度越快时，滤波器收敛到条件改变后的新稳态状态速度越快，即算法的鲁棒性越好。

实验仿真了不同增益下收敛速度相似的情况下，分别取增益G为30、50、70和90，即G为29.54 dB、33.98 dB、36.9 dB和39.08 dB，以平均稳态失调量和稳态失调范围作为指标衡量反馈抑制在稳态下的性能，具体数值见表3和表4。其中平均稳态失调量指稳态状态下失调量的平均值，稳态失调范围指稳态状态下失调量最大值与最小值的差的平均值。平均稳态失调量越小，稳态失调范围越小，助听器反馈抑制系统的性能越好。

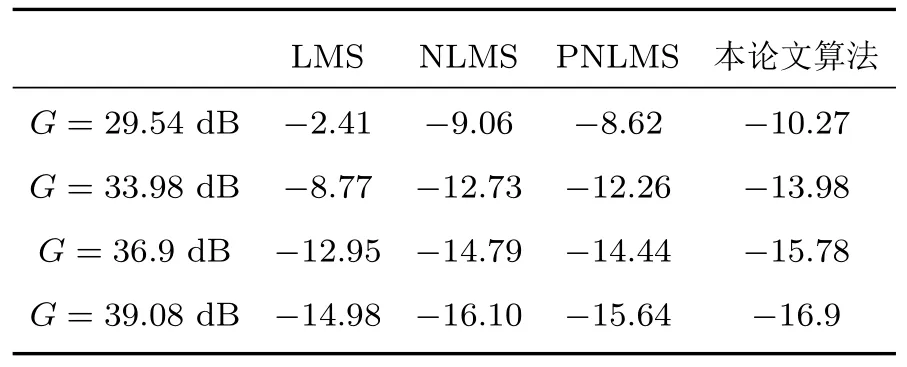
表3 平均稳态失调量Table 3 Mean steady state misalignment(单位：dB)

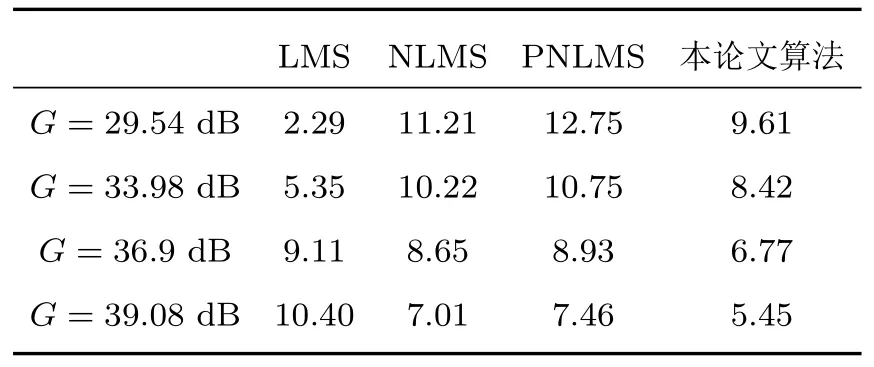
表4 稳态失调范围Table 4 Range of steady state misalignment(单位：dB)

从表3和表4可以明显观察到，随着前向增益的增大，4种算法的平均稳态失调量都随之减小，这是因为前向增益越大，受话器发出的信号也越大，从反馈路径传回传声器的反馈信号也随之增大，反馈信号在传声器处接收的信号幅度越大，而语声输入信号不变，反馈信号占比则越大，此时自适应滤波器对反馈路径的模拟则越准确，因此，平均稳态失调量随增益增大而减小。随着前向增益的增大，LMS算法的稳态失调范围增大，其他3种算法的稳态失调范围减小，这是因为除LMS外的3种的算法的步长都有对信号能量的归一化，而LMS算法的步长固定，当达到稳态的情况下，增益越大，则会使更新滤波器的信号越大，稳态失调范围也就随之增大。而其余3种算法因为对能量的归一化处理抵消了信号能量增大带来的影响，稳态失调范围与平均稳态失调量都随增益减小。在对比的几种算法中，除LMS算法外，在不同增益的情况下，基于信噪比的NLMS算法不论在平均稳态失调量还是稳态失调范围，都具有最优的性能。其中，基于信噪比的NLMS算法的平均稳态失调量和稳态失调范围性能分别较NLMS算法低约1 dB和2 dB，较PNLMS算法分别低约1.5 dB和2～3 dB。而LMS算法较为特殊，平均稳态失调量过高，性能最差，即使稳态失调范围较小，整体依然是具有最差的性能。

为进一步验证算法的性能，添加一组测试数据，在参数未进行变动的前提下，取增益G=36.9 dB的情况下4种算法的失调量数据，以平均稳态失调量和稳态失调范围作为指标衡量反馈抑制在稳态下的性能，具体数值见表5，可进一步验证基于信噪比的NLMS算法对平均稳态失调量和稳态失调范围的性能的提升。

表5 测试数据的稳态失调Table 5 State misalignment of test data

3.2.3 反馈抑制效果评估

对声反馈抑制方法研究的目的是增加系统所能达到的最大稳态增益(Maximum stable gain,MSG)，因此使用MSG作为衡量反馈抑制性能的标准。MSG表示的是系统能正常工作达到稳态的最大增益，其数值越大意味着助听器可调的增益范围越大，对听力受损越严重的佩戴者越有优势，同时在更大的范围的增益下能够达到稳态，算法的鲁棒性也越强。表6记录了在稳态失调范围相似的情况下不同算法的MSG。由此可见，基于信噪比的NLMS算法较无反馈抑制时提高了20 dB的增益，较LMS算法、NLMS算法及PNLMS算法分别提高了约12 dB、4 dB和3 dB的增益。

表6 最大稳态增益Table 6 Maximum stable gain

4 结论

本文针对助听器反馈抑制领域提出了一种基于信噪比的自适应滤波算法，以解决语声信号的相关性较大，容易使自适应滤波器出现较大失调的问题。当信噪比高时，将自适应滤波算法步长控制在一个较小值，减少算法失调；当信噪比低时，将自适应滤波算法步长控制在一个较大值，加快收敛速度。通过实验仿真，本文提出的基于信噪比的NLMS算法较传统的NLMS算法在性能上分别降低约1 dB的平均稳态失调量、2 dB的稳态失调范围，提高了4 dB的最大稳态增益，同时具有更快的收敛速度，实现了传统NLMS算法的优化。对比本文所提出的算法与其他参考算法，验证了本文提出的优化算法具有较低的失调量、较快的收敛速度，同时能够达到较高的增益，均优于其他3种算法。