基于微地震数据的增强型地热储层参数及采热的数值模拟研究

2022-11-23马子涵邢会林靳国栋谭玉阳闫伟超李四海

水文地质工程地质 2022年6期

马子涵，邢会林，靳国栋，谭玉阳，闫伟超，李四海

（1.深海圈层与地球系统前沿科学中心，海底科学与探测技术教育部重点实验室，中国海洋大学海洋地球科学学院, 山东青岛 266100；2.青岛海洋科学与技术试点国家实验室，山东青岛 266237；3.中国海洋大学海底科学与工程计算国际中心，山东青岛 266100）

地热能作为一种清洁、稳定、可再生的新型能源，符合绿色环保可持续的发展要求，被誉为21世纪最具潜力的能源之一[1]。干热岩型地热资源是指储存在地下低渗透性高温岩体中的热能[2]，约占地热资源总量的30%，相当于全球石油、天然气和煤炭能量总和的30 倍[3]。但是，干热岩储层具有埋藏深、岩石致密、渗透率极低等特点，使用传统技术难以有效开发其中的热能[4]。利用增强型地热系统（Enhanced Geothermal Systems, EGS），即使用水力压裂技术将原有储层改造为高渗透性的人工储层，而后通过水、二氧化碳等工作流体的循环注采，可实现干热岩中热能的高效开采[5]。EGS 技术作为实现深层干热岩型地热资源综合开发利用的关键技术，已经成为各国新能源发展的重点关注方向之一[6]。

利用EGS 技术提取热能是一个包含传热、渗流等多物理场耦合的复杂过程[7]，因其影响参数众多[8]，物理性质相差悬殊，时空演化不均衡等特点，通常利用数值模拟技术分析EGS 采热过程[9-10]。近年来，国内外学者提出了不同的数值模型，其中最常用的方法为等效多孔介质模型。Jiang 等[6]、Ayling 等[11]建立了用于研究EGS 采热的热流耦合模型，将热储层等效为多孔介质，进行模拟并与实际情况进行对比，验证了模型的有效性。Llanos 等[12]为库珀盆地Habanero EGS 开发了一个三维热流模型，考虑了渗透率各向异性，结果表明渗透率各向异性是控制储层流体流动的关键，同时为干热岩储层的开发设计了不同的井布局，并得出东西向交错的布局在该模型中为最优井布局。Hogarth等[13]在此模型基础上进行了单井注入和2 口井联通、闭环测试的模拟，将模型计算的生产井温度曲线与实际记录温度进行对比，验证了模拟结果的准确性。Samin 等[14]提出孔隙度均一的三维多孔介质THM 模型，储层分为基岩和裂缝，裂缝区的渗透率具有各向异性，以此模型优化裂缝区渗透率、流体注入压力、注采井距等，实现热发电性能与成本控制的综合改善。然而，均匀多孔介质模型没有考虑储层空间分布上的非均质性，过于理想化，不能精确地表征压裂改造后的储层渗流特征[15]。此外，另一种比较常用的方法为规则裂缝或随机裂缝模型，Sun 等[1]提出二维模型中储层由岩石基质和规则裂缝组成，并以此模型对地热储层中的流体流动、传热等特征进行了综合模拟，通过敏感性分析研究了EGS 采热的主控参数，结果表明THM 耦合效应对采热效率有重要影响。Xu等[2]提出由随机裂缝和岩石基质组成的模型，以此研究EGS 的热流耦合系统，将该模型应用于Habanero 热储层，对其采热过程进行模拟，应用结果表明该模型是模拟工业规模地热储层传热的有效方法。Wang等[4]提出的THM 模型由岩石基质块体和随机裂缝组成，模拟包含三维随机裂缝的地热储层的长期地热生产过程，并将其应用于澳大利亚的Habanero EGS 项目，评估了20 a 期间不同注入和生产压力下的采热量，结果表明，通过适当控制注采压差，可以实现持续稳定的供电。另外有学者利用单裂缝概念化模型研究采热过程，即认为热储层是由基质岩体和水平单裂缝组成或将裂缝简化为一维线段嵌入岩石基质网络中，Yao 等[16]在三维热流单裂缝模型基础上，研究区域流动方向对采热的影响，结果表明，采热可持续性随着区域流动方向和2 井中心连线的夹角的增加而增加。Li 等[17]在THM 耦合单裂缝模型基础上进行开发过程研究，发现高渗透率或大孔径会导致过早发生热突破，因此要在流动和传热之间进行权衡。然而，在这些模型中单一或者规则的裂缝分布过于理想，不能体现储层中裂缝的真实情况；随机裂缝相对灵活，但自由变量过多、模型数据量大、试验数据缺乏。

尽管已经开展了大量干热岩EGS 多物理场耦合的数值模拟工作，但由于改造后的渗透率通常极为复杂，常规方法难以描述，因此准确地估计储层中的热量提取过程仍然存在大量挑战。近年来，Xing 等[8-9]利用微震数据计算出地热储层的渗透率分布，为干热岩开采设计了8 井布局，模拟结果展示了地热储层中流场和温度场随时间的演化。李庭樑等[15]结合地质背景和压裂数据，计算出渗透率等水动力学参数的分布，并对热储进行数值模拟，将其结果与分块均质热储进行比较，结果表明热储的非均质性会导致EGS 采热性能显著下降。Xu 等[18]利用水力压裂过程中记录的微震事件生成了裂缝模型，并将该方法应用于Habanero 储层，证明了 Habanero 井之间的连通性。Fang 等[19]分别利用基于立方定律的等效多孔介质方法和离散裂缝网络方法估算压裂改造后的储层渗透率，结果表明储层中渗透率最高的区域即微震最密集的区域。以上研究表明水力压裂诱发微地震的分布可以较为准确地表征储层改造后的渗透率，微地震分布优势的方向也即储层中流体流动的优势路径。目前利用微地震数据评估渗透率也存在不足，如网格分布和震源精度的限制等。可通过优化网格划分、改善定位方法等提高渗透率评估的准确性。

基于上述研究，本文以澳大利亚库珀盆地的Habanero 热储为研究区，创新性地构建了微地震监测数据与储层渗透率之间的等效关系并建立了不同的热储模型，包括分区均质模型和非均质模型；利用自主研发的多物理场耦合软件PANDAS 对不同模型中渗流场、温度场和生产井井底温度的变化等进行了数值模拟、分析比较，探究采热性能的差异。

1 理论与方法

本文使用的模拟工具为自主研发的PANDAS，这是一种基于有限元和格子玻尔兹曼方法（Lattice Boltzmann Method，LBM）的数值模拟程序；其中热-流动耦合数值模拟模块[20]将应用于Habanero 地热储层开发中的有限元模拟及评估研究。该模型基本假设为：

（1）干热岩储层中充满单相的饱和流体水，且流体在储层中的流动遵循达西定律；

（2）流体和岩石间的换热通过对流和传导实现；

（3）不考虑流体与矿物的物理化学反应。

1.1 连续性方程

流体在多孔介质中的流动可以表示为：

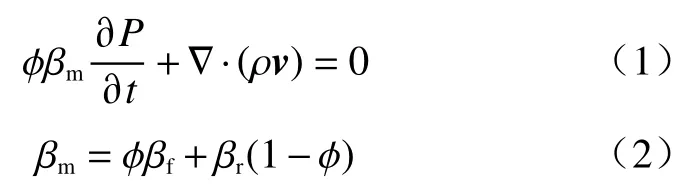
式中： φ—孔隙度；

βm—综合压缩系数/Pa-1；

βf、βr—流体和基岩的压缩系数/Pa-1；

P—流体压力/Pa；

ρ—流体密度/（kg·m-3）；

v—流体流速/（m·s-1）。

遵循达西定律的单相流体的流动控制方程为：

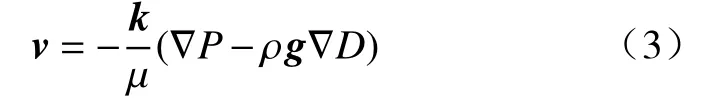
式中：k—多孔介质的渗透率/m2；

μ—流体的动力黏度/（Pa·s）；

g—重力加速度/（m·s-2）；

D—深度/m。

1.2 多孔介质中的对流-传导换热方程

多孔介质中基质和流体能量平衡方程分别为：

式中：C—比热/（J·kg-1·K-1）；

λ—导热系数/（W·m-1·K-1）；

T—温度/K；

r—岩石基质；

f—流体。

从宏观角度出发，假定EGS 各阶段中局部处于热平衡状态，即Tr=Tf=T。联立式（4）和式（5），多孔介质中的传导-对流换热控制方程为：

式中：m—基质和流体的混合系统。

2 研究区概况

库珀盆地位于南澳大利亚东北部，如图1 所示。据资料显示，库珀盆地下方3 500～4 500 m 范围内埋藏有大量的高温花岗岩，温度约为250 °C[21]，是其他地区相同深度花岗岩温度的2 倍。花岗岩岩体上方覆盖着约3 500 m 厚的沉积盖层，其主要由低孔、低渗的碎屑岩和煤系夹层组成[12]，是花岗岩基底天然的“绝热屏障”。

图1 库珀盆地热储层研究区域（修改自文献[12，24]）Fig.1 Geothermal reservoir region to be studied in Cooper basin (modified from [12, 24])

Habanero 3 号井（H03）位于1 号井东北方向约560 m处，井深约4 221 m。在2008年对3 号井进行了水力压裂[22]。并对1 号井和3 号井进行了时长为42 d 的闭环流动测试。实测数据表明，1 号井井口压力为44.5 MPa，3 号井井口压力为33.5 MPa，注采流量为15.5 kg/s。

水力压裂诱发的微地震的空间分布表明存在呈近水平结构的Habanero 断层[23]。测井资料表明，该断层是构造成因，水力压裂重新激活并扩展了之前存在的裂缝，扩大了储层高渗区域[25]。本文将以库珀盆地现场水力压裂及相关联通试验为基础，开展数值模拟评估研究。

3 Habanero EGS 数值模型

3.1 三维数值模型

基于Habanero 地热储层的地质构造特征及水力压裂改造效果，建立了三维数值模型。该模型在x，y和z方向的模型尺寸分别为1 200，1 500，500 m。模型在水力压裂区划分较密，网格尺寸为2.5 m，其他区域的网格尺寸由压裂区向外逐渐变大，在15～20 m 之间。模型计算深度为地下4 000～4 500 m，如图2（a）所示。

图2 分区均质模型和剖面图Fig.2 Homogeneous model (a) and homogeneous model profile view (b)

3.1.1 分区均质模型

根据库珀盆地现场资料及研究成果，将研究区简化为从上至下分为3 层的三维模型，如图2（b）所示。上层的深度为4 000～4 245 m，为未压裂的致密花岗岩；中间层深度4 245～4 255 m，厚度为10 m，为孔隙度和渗透率较高的改造区；下层的深度为4 255～4 500 m，为未压裂的致密花岗岩。

3.1.2 基于微地震数据的非均质模型

微震可以反映改造过程中岩石破裂发生的位置及扩展范围，故本文利用已知地质信息、微震监测数据构建Habanero 非均质热储模型。本文的数据为Geodynamics 公司在Habanero 1 号井水力压裂过程中记录的诱发微震事件。研究表明，微震点的密集程度可以用来表征储层内的渗透率分布，一般认为，微震分布密集区域的渗透率要高于微震分布稀疏区域[15]。因此，本文基于Habanero 热储区岩石破裂的机理，根据微震点到模型中各个节点的距离建立了三维非均质储层渗透率模型。

基于微地震数据的非均质模型使用的网格模型与分区均质模型使用的网格相同。在本文的计算方法中，渗透率是网格节点到微震点距离的指数函数，各个节点处的渗透率由2 部分组成：第1 部分为初始渗透率，第2 部分通过计算各个微震事件到该节点的距离进行评估。具体计算方法引自Xing 等[8]。在有限元计算中对微震事件和渗透率计算节点的加权距离评估：

式中：K—节点处的渗透率/m2；

K0—初始渗透率/m2；

A—震级对渗透率的影响系数（此处A=1.0×10-15）；

dx、dy、dz—考虑破裂面倾角影响的微震事件与网格节点的距离；

B1、B2、B3—微震事件在x、y、z方向上影响范围的参数。

3.2 模型参数

根据测井数据，库珀盆地在3 500～5 000 m 深度范围内，初始温度和压力随深度而变化，温度梯度为31 °C/km，压力梯度为8.6 MPa/km。将模型上下表面的压力和温度设置为恒定，上表面压力为71.8 MPa，温度为240.1 °C，下表面压力为76.1 MPa，温度为255.6 °C。根据Llanos 等[12]和O’Sullivan 等[26]的研究，模型基于所有侧面没有热量或质量的传递建立，因此模型四周设置为封闭边界。

分区均质模型中除渗透率以外，其他的岩石物理性质参考Llanos 等[12]的研究，如表1 所示，在基于微地震数据的非均质模型中，渗透率通过微震监测数据进行计算，其他岩石物理性质参数与分区均质模型保持一致。

表1 分区均质模型中岩石物理性质参数Table 1 Parameters of rock in the zonal homogenization model

在2 个模型中，均使用水作为循环工作流体。在模型初始状态时，假设储层中水的温度与其所处的围岩温度相同，注入工作流体温度为90 ℃。表2 为循环工作流体的物理性质参数。

表2 循环工作流体的物理性质参数Table 2 Parameters of the circulating fluid

3.3 模型渗透率的确定

利用2008年8月进行的Habanero 1 号井（H01，注入井）与Habanero 3 号井（H03，生产井）（图3）的闭环流动现场测试数据，对研究区渗透率进行校正。以现场实测压力、流量数据为基础，确定模型中的井底压力，调整模型中改造区的渗透率，并对比模拟流量与实际流量。

图3 模型中H01、H03 位置Fig.3 Locations of H01 and H03 in the model

3.3.1 分区均质模型渗透率

Habanero 地热储层是致密花岗岩体，地层初始渗透率低，约为1.0×10-20m2。根据水力压裂产生的微震点的空间分布，结合Llanos 等[12]的研究，Habanero 地热储层压裂后渗透率存在各向异性，y方向和x方向的渗透率之比为2∶1，z方向渗透率较低，在此基础上利用实测流量对渗透率进行调整。表3 为在不同渗透率下，生产井中的模拟流量与实际流量的对比，由此可得，压裂后改造区渗透率的最佳拟合值为x方向1.3×10-13m2，y方向2.6×10-13m2，z方向4.0×10-14m2，10 m 厚的改造区以外渗透率均为1.0×10-20m2。

表3 分区均质模型不同渗透率下生产井中的模拟流量与实际流量Table 3 Simulated flow and actual flow of production wells in the homogeneous model with different permeabilities

3.3.2 非均质模型渗透率

在非均质模型中，通过调整相关参数，得到不同渗透率下生产井中的模拟流量（表4），并与实际流量进行对比。模型中渗透率的最佳拟合相关参数为B1=5.0×10-5、B2=2.0×10-5、B3=2.5（B1、B2、B3是微震事件在x、y、z方向上影响范围的权重参数，库珀盆地水力压裂微震事件以水平分布为主，因此设置Habanero地热储层压裂效果对节点至微地震点x、y方向的距离较为敏感）。该情况下，渗透率分布见图4 和图5，图4 显示整体模型的渗透率的分布，图5 为渗透率分布的等值面图，主要显示水力压裂区的渗透率分布。

表4 非均质模型不同渗透率相关参数下生产井中模拟流量与实际流量Table 4 Simulated flow and actual flow of production wells in the heterogeneous model with different permeability related parameters

图4 （a）非均质模型的渗透率分布图和（b）渗透率剖面图Fig.4 Permeability distribution for the heterogeneous model (a)and permeability profile (b)

图5 （a）渗透率分布等值面图和（b）渗透率等值面的剖面图Fig.5 Contour surface view of permeability distribution (a) and isosurface profile of permeability distribution (b)

4 结果与讨论

4.1 流场

图6（a）（d）是2 种模型中深度为4 250 m 截面的流速分布，可以看出，2 种渗透率模型中流速较大的是2 口井之间的连线及其附近的区域，说明储层内流体流动的优势路径为两井之间的连通区域。对比2 种渗透率模型的平面流速，分区均质模型中该深度截面流速较大区域的范围要比非均质模型更大。原因在于2 种模型渗透率的不同，分区均质模型10 m 厚改造区内是具有各向异性的均一分布渗透率，x方向1.30×10-13m2，y方向2.60×10-13m2，z方向4.0×10-14m2。非均质模型中渗透率由微震事件及破裂面决定，如图7 所示，注入井附近渗透率最大，约为9.4 ×10-13m2，从注入井向生产井方向渗透率逐渐变小，在生产井附近渗透率约为1.0×10-14m2，这是因为微震事件发生的集中区域为注入井附近，并由此向外延伸，在微震事件发生较多的区域渗透率较高，储层中2 井连线及其附近的区域表现出流动优势，远离注入井的区域由于微震事件较少，所以裂隙较少、渗透率较低，流速也小。非均质模型中除注入井附近，其他位置渗透率要比分区均质模型中低，因此分区均质模型井间流速大于非均质模型。

图6 不同模型的流速分布（上为分区均质模型，下为非均质模型）Fig.6 Velocity distribution of different models (the upper is the zonal homogeneous model and the bottom is the heterogeneous model)

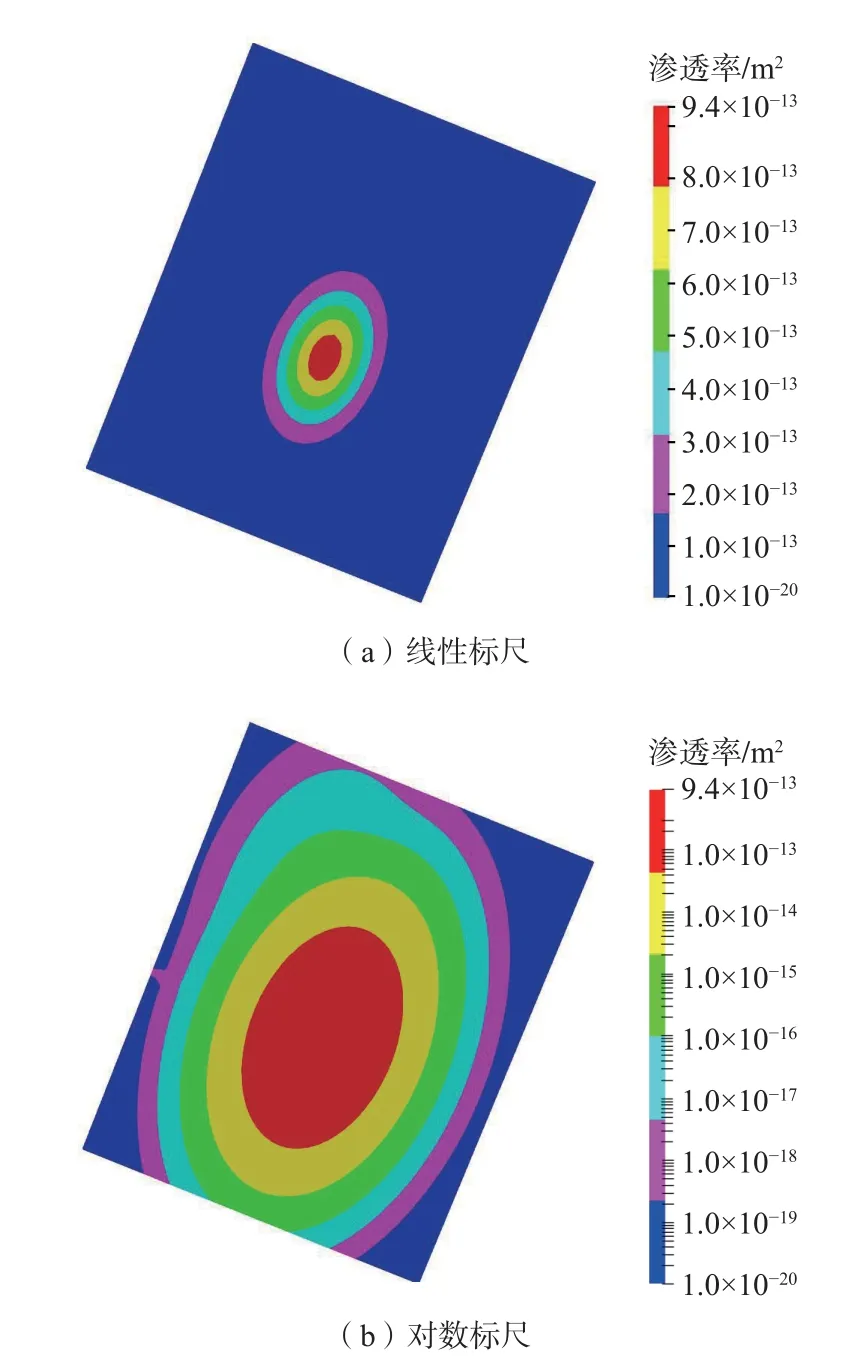
图7 非均质模型中z=4 250 m 剖面渗透率分布Fig.7 Permeability distribution at the section z=4 250 m in the heterogeneous model

由图6（b）（e）可知，在垂直方向上，分区均质模型的流动区域限于10 m 厚的改造区内，而非均质模型在深度方向上流体流动区域集中于该区域，但不限于此，这是因为微震事件在垂向上有较大延伸。

4.2 温度场

温度分布等值面图，范围为90～230 °C（图8），总的来看，在初始运行阶段，冷流体自注入井进入压裂改造区，由于与周围高温岩体进行了热交换，注入井附近岩体温度接近注入温度90 °C。随着注入流体的增多，低温区（90～115 °C）逐渐扩大，并沿优势流动通道向生产井扩散。

图8 不同模型温度随时间变化的等值面图Fig.8 Isosurface of temperature variation with time in different models

对比来看，分区均质模型中的冷流体从注入井向改造区中流动扩散，逐渐形成一个近似扁椭圆体的低温区，近y方向上的低温区影响范围大于近x方向的影响范围。在深度方向上，低温区范围基本限制在深度4 245～4 255 m 的10 m 厚改造区内。

在非均质模型中，注入井两侧冷流体流动的影响范围与均质模型相比，冷流体向着生产井流动的趋势更加明显。近y方向上的低温区影响范围同样大于近x方向的影响范围。但深度方向对比来看，低温区影响范围不再局限于10 m 厚的范围。这是因为水力压裂形成的微震事件在深度上的分布范围较广，微震发生的区域内储层渗透率也随之变大。

4.3 采热性能

2 种模型的生产井井底温度在30 a 间的变化情况见图9（a）。分区均质模型30 a 间温度变化趋势为前期（0～7.9 a）保持不变，之后（7.9～30 a）缓慢下降，非均质模型30 a 间温度变化趋势为前期（0～8.5 a）保持不变，之后（8.5～30 a）快速下降，且下降速度逐渐变慢。系统运行到30 a，分区均质模型温度下降到220.9 °C，下降了26.9 °C，非均质模型温度下降到170.0 °C，下降了77.8 °C。

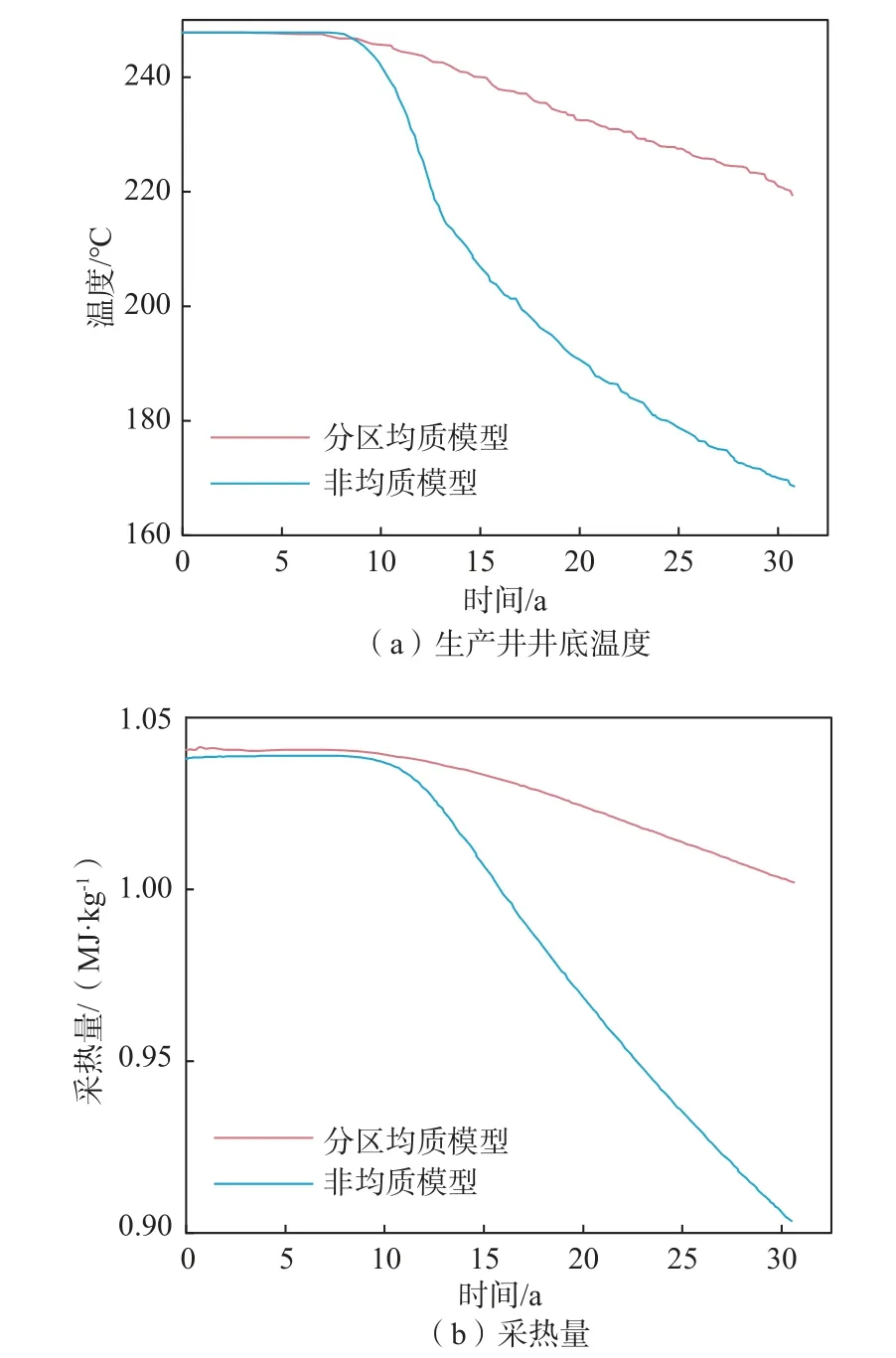
图9 分区均质和非均质模型生产井井底温度和采热量对比Fig.9 Comparison of the bottom hole temperature of production wells and heat extraction comparison in the two models

对比来看，2 种模型生产井初始温度保持不变的时间十分接近；后期分区均质模型温度下降少，非均质模型下降多。由此分析，分区均质模型略早下降0.6 a，即热突破时间稍微早一些，这是分区均质模型生产井附近渗透率比非均质模型大导致的。非均质模型温度下降幅度比分区均质模型大，下降速度比非均质模型快，这是由于非均质模型的高渗区集中于2 口井连通区域内，使得非均质模型中优势流动通道显著，所以温度下降更快。

2 种模型单位质量流体采热量的对比关系，即采出热量与采出质量的比值[27]，见图9（b）。分区均质模型和非均质模型在储层模型运行初期单位质量流体采热量比较接近，约为1.04 MJ/kg，分区均质模型初始时间略高。之后随着生产井温度的快速下降，2 种模型的单位质量流体采热量也迅速降低，对比来看，两种模型单位质量流体采热量下降发生的时间接近，分区均质模型采热量下降速度很慢，在模型计算到30 a时，单位质量流体采热量降低至1.003 MJ/kg，降低了3.74%；非均质模型采热量下降速度较快，在模型计算到30 a 时，采热量降低至0.906 MJ/kg，降低了12.72%。从采热量对比看，分区均质模型在热储层运行期间采热量变化相对更稳定，非均质模型采热量降幅较大。

对比生产井温度曲线和采热量曲线，分区均质模型的模拟结果相比于非均质模型结果来说，温度下降幅度小、单位质量流体采热量高，但由微震分布可知实际储层中的渗透率分布并不均匀，2 井之间优势流动通道效应显著，因此分区均质模型的模拟单位质量流体采热量高于实际单位质量流体采热量。

原始地热储层压裂后，激活并扩展了先存裂缝，在水压足够高时产生新的裂缝，提高了储层中尤其是近井区域的渗透率，形成优势流动通道，改善了储层连通性。此外，水力压裂后储层渗透率具有显著的渗透率各向异性，是影响干热岩开发动态的重要因素之一[28]。相比分区均质模型，非均质模型中的优势流动通道、渗透率各向异性更加明显，更加符合压裂后的储层实际情况，因此在实际应用中，非均质模型的模拟结果对实际工程更具参考意义。