基于Green-Ampt模型的多层结构边坡降雨入渗改进计算方法及稳定性影响研究

宋宜祥，尹子航，黄 达

（河北工业大学土木与交通工程学院, 天津 300401）

土质边坡的稳定性分析是岩土工程中十分重要的研究课题。非饱和土质边坡在天然状态下常具有较高的稳定性，但在降雨的作用下，边坡表层土体的饱和度增加，边坡内部的孔隙水压力增大，基质吸力有所减少，边坡稳定性将大大降低[1]。降雨强度、历时、土体力学性质等多种因素都会对边坡的稳定性产生影响[2-3]。根据调查，在全国290 个县发生的地质灾害中，90%的滑坡由降雨诱发[4]。因此对降雨作用下非饱和土质边坡稳定性影响的研究具有重要意义。

Green 等[5]在考虑薄层积水的情况下，基于毛细管理论提出一种新的入渗物理模型—Green-Ampt（GA）模型。G-A 模型很好的预测了湿润锋的发展，但实际上湿润锋以上的土体并非完全饱和。基于此，彭振阳等[6]根据Richards 方程和入渗实验对入渗过程的精确模拟，将入渗面以下的均质土体分为饱和层、过渡层和初始层；并发现过渡层饱和含水率变化至初始含水率符合椭圆形曲线分布。苏永华等[7]、李诚诚[8]基于上述含水率的分层假定改进G-A 模型，提出均质边坡降雨入渗深度及其稳定性的计算方法，并给出过渡层厚度与湿润层厚度之间的关系。胡庆国等[9]基于降雨入渗机理及均质土体雨水入渗深度理论计算公式，提出多层结构土质边坡降雨入渗模型。

虽然上述学者已经将G-A 模型推广至多层结构土质边坡，但模型精度不足。为此很多学者对渗流过程进行进一步研究，并将其细分为不同阶段。如王继华[10]分析均质土体中雨水的入渗过程，将非饱和土边坡降雨入渗过程分为2 个阶段，分别为降雨强度控制阶段和土体渗透系数控制阶段，2 个阶段的交点为积水点。积水点形成时刻的研究对于多层结构土质边坡稳定性的评价格外重要[11-12]。但已有的计算方法（多层结构土）却忽略上述事实，对计算模型的精度产生较大影响。

上述学者在对雨水入渗深度的研究中，取得了一系列的成果。在此基础上，学者对边坡稳定性进行分析。 Fredlund 等[13]提出非饱和土体抗剪强度理论，将双应力状态变量与多相连续介质学进行结合。方薇[14]提出非饱和土的非线性抗剪强度包络壳模型，根据土水特征曲线参数计算该模型抗剪强度。黄梦宏等[15]在利用极限平衡法求解稳定性系数时，通过引入载荷系数将其转化为求解一系列线性规划问题。

学者已认识到过渡层存在的事实，并给出过渡层厚度与湿润层厚度间的关系，将入渗理论推广至多层结构土。但这些研究很少考虑降雨作用下多层边坡土体中基质吸力随土体含水率变化的事实，同时对边坡潜在滑动面位置随降雨历时的变化考虑不足。

基于此，本文将在考虑基质吸力变化与层间积水形成的情况下，结合饱和层内沿边坡内部渗流管网向坡底流失部分雨水的事实，将入渗过程分解为若干个子过程，并基于G-A 入渗模型对胡庆国等[9]提出的传统多层结构土质边坡降雨入渗深度计算方法提出改进并对子过程进行求解，最后将其合并为整体入渗过程的解。在此基础上对层间积水点的形成时刻进行预测，进而分析雨水入渗深度与时间的关系，并研究随降雨历时增长，降雨强度与雨水入渗深度对边坡不同位置处（湿润锋、饱和层）稳定系数的影响。以达到对潜在滑动面位置随降雨历时动态变化分析的目的，进一步提高传统多层结构边坡入渗计算方法的精确度与适用范围。

1 非饱和-饱和渗流分析

1.1 降雨作用下土体含水率变化规律

G-A 模型（图1）对湿润锋的发展进行了很好的预测，其入渗模式可以表示为:

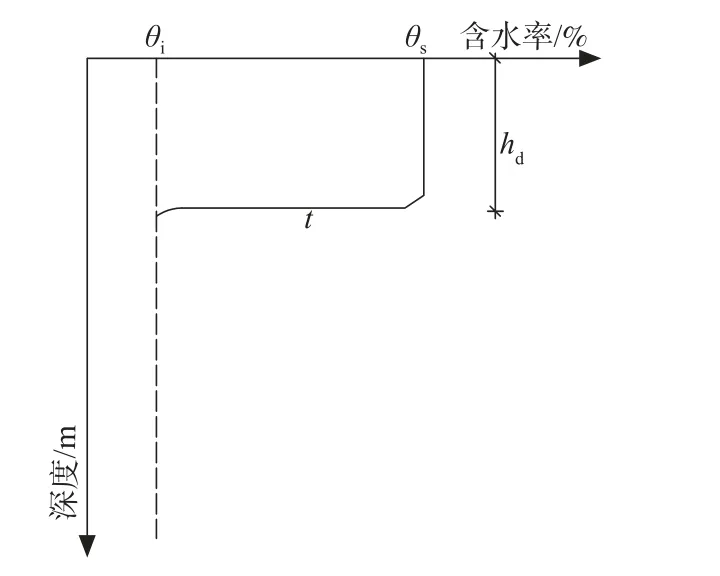
图1 G-A 入渗模型Fig.1 G-A infiltration model

式中：i—雨水入渗强度/（m·s-1）

ks—土壤饱和渗透系数/（m·s-1）；

sf—湿润锋处基质吸力/m；

hd—湿润锋深度/m。

彭振阳等[6]在G-A 模型基础上提出含水率的分层假定模型（图2），苏永华等[7]、李诚诚[8]给出饱和层厚度（hs）与湿润层厚度（hd）之间的关系，如式（2）所示。

图2 降雨入渗过程剖面图Fig.2 Profile of rain fall infiltration process

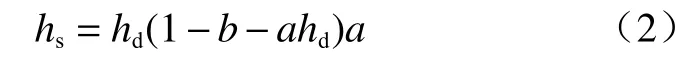
式中：a、b—各层土的相关系数。

胡庆国等[9]提出多层结构土质边坡降雨入渗模型（图3）；图3 中，h1、h2分别为第1、2 层土体厚度，θi1、θi2、θi3分别为不同土层初始饱和度，θs1、θs2、θs3分别为不同土层饱和度。第1 层土的雨水渗流强度为i1且湿润锋位于该土层时，湿润锋到达第1、2 层分界面时间（t1）为：

图3 多层结构土质边坡含水率分布示意图Fig.3 Schematic diagram showing water content distribution of soil slope with the multi-layer structure

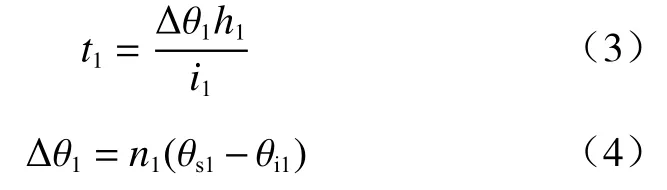
式中：Δθ1—第1 层土体饱和度差值；

n1—第1 层土的孔隙率。

降雨入渗的深度（hd1）为：

1.2 基于G-A 模型改进多层结构边坡入渗理论

Mein 等[16]将G-A 模型应用到降雨入渗分析，并考虑到降雨入渗过程分为雨水入渗强度控制阶段和土体入渗能力控制阶段的情况（图4）。

图4 入渗率-时间关系曲线Fig.4 Relation between infiltration rate and time

基于此，本文提出一种新型多层结构土质边坡降雨入渗模型（图5）。如图5 所示，计算模型分为3 层，横坐标为含水率的变化，纵坐标表示雨水入渗深度。hd1、hd2、hd3分别为第1、2、3 层土体中湿润锋的深度，hd1（1）、hd1（2）分别为第1 层土体中第1 阶段与第2 阶段湿润锋深度，hd2（1）、hd2（2）分别为第2 层土体中第1 阶段与第2 阶段湿润锋深度。假设边坡倾角为α，降雨强度为q，降雨初期，表层土体处于非饱和状态，雨水入渗强度小于土体入渗能力，雨水全部渗入土体。此时，降雨在垂直于坡面方向的入渗强度（i1）为：

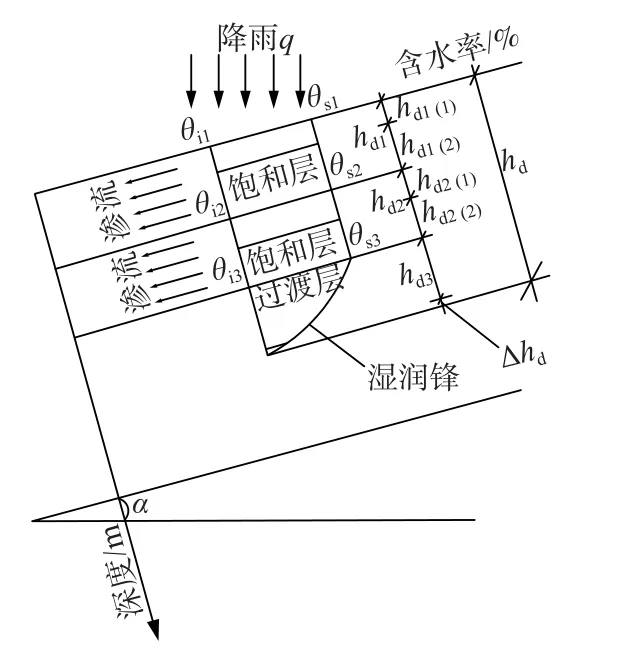
图5 多层结构土质降雨入渗过程剖面图Fig.5 Section of soil rainfall infiltration process of the multi-storey structure

随着降雨历时的增长，土体入渗能力随着地表土体的饱和而减小，直至小于降雨强度。此时雨水入渗强度由土体入渗能力控制，考虑不断变化的基质吸力，垂直于坡面方向的入渗强度（i12）为：

式中：sf1—第1 层土湿润锋处平均吸力/m；

k1—第1 层土体饱和渗流系数/（m·s-1）。

由降雨入渗强度连续性可知存在临界时刻tp1（积水点）使得i1=i12，则tp1时雨水入渗深度（hdp1）为:

其中：

将式（8）代入式（3）可得临界时刻tp1为：

湿润锋到达第2 层土体的时刻为t1，若tp1＞t1，取tp1=t1。故当降雨历时t＜tp1时，将式（6）代入式（4）可得此时湿润锋深度（hd1）为：

当降雨历时tp1＜t＜t1时，伴随着入渗过程的发展，土质边坡开始出现积水点（tp1），过渡层作用于饱和层的吸力效能不断减少，加之受边坡几何条件与重力的影响，假设该部分雨水（饱和层）沿边坡内部渗流管网平行于边坡表面向坡底流动（图5）。

由Darcy 定律分析各向同性边坡体可得，第1 层土体饱和层排出雨水的强度（ip1）为：

式中：hs1—第1 层土体中饱和层厚度/m。

将式（2）代入式（11）可得：

式（7）与式（12）的差值即为第1 层土体第2 阶段的有效降雨入渗强度（i1(2)）：

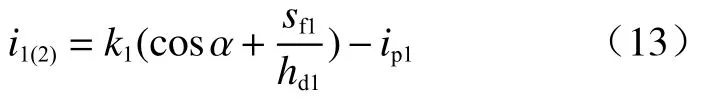
第1 层土体的渗流速率（v1）为：

降雨入渗深度（hd1）为：

式中：Δt—计算时间步长/h；

j—所取计算时间步长数量。

计算时，首先根据式（9）计算积水点形成的时刻tp1，并根据tp1将入渗过程分为2 个阶段，分别用式（6）、式（13）计算雨水入渗强度控制阶段的入渗强度、土体入渗能力控制阶段的入渗强度（考虑变化的基质吸力）。

当降雨历时t1＜t＜tp2时,其中tp2为第2 层土体中积水点的形成时刻，渗流初期，第2 层土体入渗能力大于雨水的入渗强度，层间雨水全部渗入土中，此时:

式中：i2—第2 层土体雨水入渗强度/（m·s-1）。

当降雨历时tp2＜t＜t2时，其中t2为雨水到达第2 层土与第3 层土交界面处的时刻，伴随着入渗过程的发展，土体入渗能力越来越小，直至小于雨水渗流强度，此时层间开始出现积水点。将第2 层土体参数代入式（13），得到：

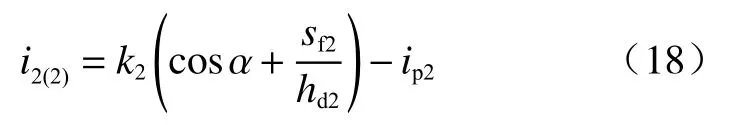
式中：sf2—第2 层土湿润锋处的平均吸力/m；

i2(2)—第2 层土体的有效雨水入渗强度/（m·s-1）；

k2—第2 层土体饱和渗透系数/（m·s-1）；

hd2—第2 层土体中湿润锋的深度/m；

ip2—第2 层土体饱和层排出雨水的强度/（m·s-1）。

将式（17）与式（18）依次代入式（14）、式（15）与式（16），得到hd2。基于此，将此方法推广至多层结构土质边坡。

（1）根据降雨时间选择合适的时间步长，并大致判断出雨水入渗深度，并根据土层的入渗率，饱和度以及其他拟合参数计算湿润锋深度。

假设降雨强度为0 层土的渗透率，记为k0。首先将第1,2,3,···,n层土的渗流过程分为雨水入渗强度控制阶段和土体入渗能力控制阶段，并计算第r层土的临界时刻tpr。若tpr＞tr，取tpr=tr，表示第r层土体只存在雨水入渗强度控制阶段。然后分别计算每层土体中各个阶段的雨水渗流强度，并根据式（3）分别计算雨水在不同土层中的入渗时间t1,t2,t3,···,tn-1，进而得出湿润锋到达第n与n+1 土层交界面的时间为：

根据式（19）得到湿润锋到达第n与n+1 土层交界面时间，据此初步估计湿润锋所在土层。

（2）根据上述计算结果推测湿润锋所在土层。结合降雨历时，选择合适的时间步长Δt，计算此时的湿润锋深度：

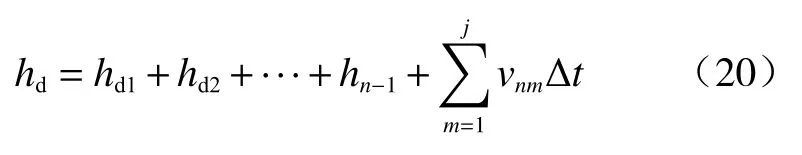
在推导多层结构土质边坡降雨入渗深度理论公式时，并没有考虑边坡表面产生厚积水情况，这是因为当降雨强度大于表层饱和渗透系数k1时，雨水的入渗强度最大为k1，边坡与地面存在一定的角度，边坡表面无法聚集雨水，仅存在一层薄积水[17]。同时，仅表层土体在降雨入渗过程中可达到完全饱和。降雨后湿润区内土体的体积含水率大约为0.8～0.9 倍的饱和土体含水率[18]。

2 非饱和土边坡的稳定性分析

2.1 边坡稳定性的极限平衡法

降雨入渗条件下，非饱和多层结构土质边坡多发生平行于边坡表面的浅层滑坡（湿润锋处破坏）[19-20]。此外，当饱和层到达土层交界面时，易在土层交界面处形成积水，甚至产生平行于坡面的渗流，故饱和层与过渡层交界面亦可能成为潜在的滑动面[21]。以单位宽度、长度为L的边坡体作为研究对象，分别将饱和层面与湿润锋面作为潜在滑动面，采用有限元软件分析降雨入渗过程中滑动面随降雨历时增长的动态变化过程[22]。

采用饱和层处稳定系数（Fsm）与湿润锋处稳定系数（Fsf）评价边坡的稳定性。当潜在滑动面位于湿润锋处时，对胡庆国等[7]提出的关于土质路堑边坡的稳定系数计算方法进行改进并计算。胡庆国等[7]给出土质路堑边坡稳定性系数（Fs）的计算公式：

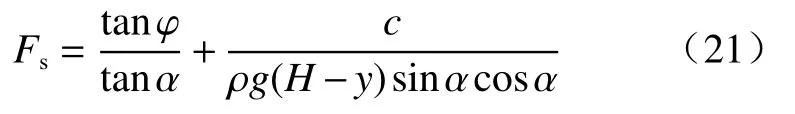
式中：c—土体有效黏聚力/kPa；

φ—土体有效内摩擦角/（°）；

ρ—水的密度/（kg·m-3）；

H—路堑边坡的高度/m；

y—未被雨水浸湿的土体厚度/m。

为将式（21）推广至普通边坡，本文将水的重度（ρg）替换为对应土体的饱和重度（γs），并引入湿润锋深度（hd）这一变量。此时湿润锋影响下的边坡稳定性计算公式为：

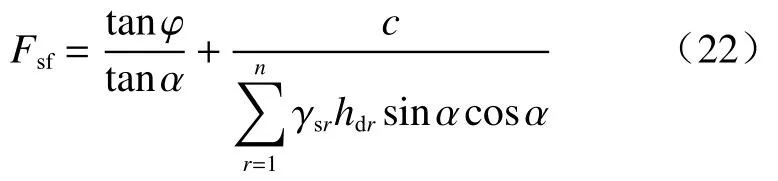
式中：r—第r层土体；

γsr—第r层土体饱和重度/（kN·m-3）；

hdr—第r层土体中浸润锋深度/m。

潜在滑动面位于饱和层处时，对李诚诚[6]提出的以交界面为潜在滑动面时边坡稳定系数计算方法进行改进与求解，此时饱和层影响下的边坡稳定性计算公式为：

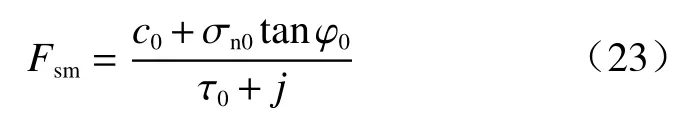
式中：c0—饱和土有效黏聚力/kPa；

σn0—饱和层面作潜在滑动面时土体正应力/kN；

φ0—饱和土有效内摩擦角/（°）；

τ0—饱和层土体重度沿坡面的分力/kN；

j—作用于饱和层的渗透力/kN。

降雨历时t＜tp1时，饱和层土体重度沿坡面方向的分量与饱和层渗透力的计算公式[5-6]为：

式中：γw—水的重度/（kN·m-3）；

hs1—第1 层土饱和层厚度/m；

γs1—第1 层土的饱和重度/（kN·m-3）。

故当t＜tp1时，饱和层处稳定系数（Fsm）为：

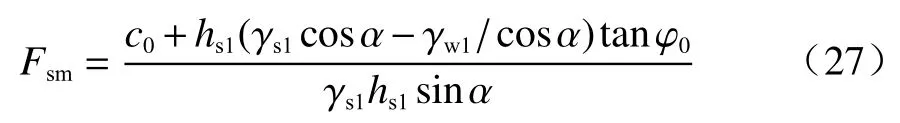
降雨历时tp1＜t＜tp2时

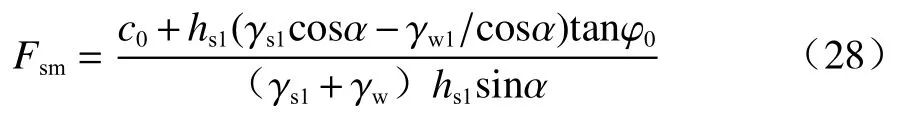
降雨历时t＞tp2时，土层交界面处形成积水，此时积水点的发展强度为：

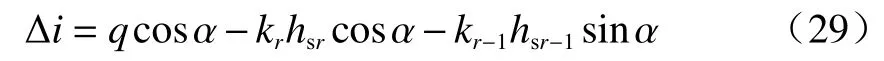
式中：kr—第r层土体的饱和渗透系数/（m·s-1）。

将式（29）代入式（4）可将积水强度换算为等价的湿润层厚度：

将式（30）代入式（2）可将积水强度换算为等价的饱和层厚度：

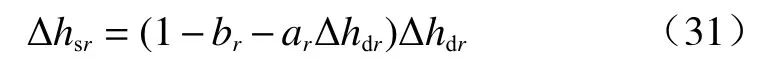
此时饱和层内平行于坡面的渗流力为：

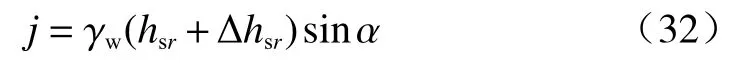
饱和层土体重度沿坡面方向的分量为：

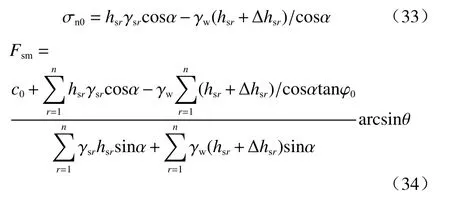
某一降雨历时下，边坡整体稳定系数Fs为Fsf和Fsm较小值即：

利用式（22）、（34）、（35）分析潜在滑动面随降雨历时增长的动态变化过程，进而对边坡稳定性进行评估。该方法既考虑了降雨过程中土层交界面处存在积水点的情况，又考虑了不同的潜在滑动面，使得边坡稳定性评价更加完善、更加符合实际。

3 模型验证与分析

3.1 模型建立与计算参数的确定

选择文献[7]中的边坡计算模型与实验数据进行验证，该边坡分别由坡积土、风化土、基岩构成（图6）。如图6 所示，模型坡比为1∶1.5，边坡高度为5 m，坡积土与风化土体的厚度均为1 m。渗流计算时，将模型底部以及两侧设为不透水边界，并将降雨强度边界转化为单位流量边界施加于计算模型表面。边坡的力学参数如表1 所示。

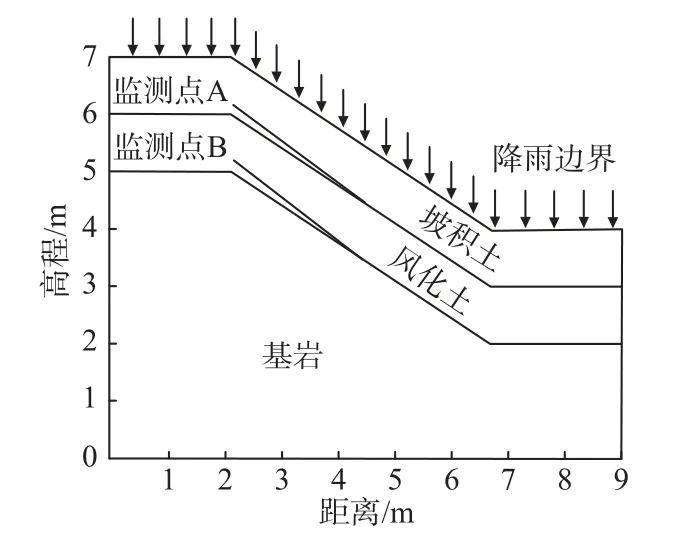
图6 计算模型Fig.6 Calculation model

表1 土体力学参数Table 1 Mechanical parameters of soil

本次计算降雨强度为8×10-6m/s。由于边坡土体的压实度[23]与粒度的分布[24]均会影响土层渗透系数的变化，为此坡积土、风化土、基岩的饱和渗透系数分别取为5.0×10-5，1.39×10-7，1.2×10-8m/s。

3.2 边坡降雨入渗深度与稳定性分析

3.2.1 降雨入渗深度

基于有限元软件GEO-Studio 进行数值模拟，并利用式（20）计算不同时刻的雨水入渗深度，计算结果如图7 所示。由图7 可知，降雨历时5.5 h 时，雨水入渗深度为1 m，雨水到达坡积土与风化土交界面，本文所提计算模型与数值模拟结果基本一致，证实了本文模型的正确性。

图7 降雨入渗深度理论的数值模拟结果、本文结果、文献[7]结果曲线Fig.7 Numerical simulation results of the theory of rainfall infiltration depth, results in this paper, and results in literature [7]

降雨历时7 h 时，雨水入渗深度为1.12 m，此时本文改进理论模型计算值与数值模拟值结果开始出现偏差，但总体趋势基本吻合。

将本文改进理论模型的计算结果与文献[7]的结果进行对比，二者在降雨5.5 h 之前较吻合，这是由于降雨强度小于坡积土饱和渗透系数时，tp1＞t1，此时取tp1=t1，改进理论模型仅存在第1 阶段，退化为文献[7]的模型。但在降雨5.5 h 之后，文献[7]的结果与模型的数值模拟结果开始出现偏差，而本文改进理论模型出现偏差的时刻较晚，约在7 h 左右。造成这种现象的原因是，降雨5.5 h 时，湿润锋到达交界面处，此时第2 层土体入渗能力大于雨水的入渗强度，交界面雨水全部渗入土中，积水点并未形成。改进的理论值更好的预测了积水点形成于坡积土与风化土渗透能力相等时，而非湿润锋到达土层交界面的时刻。

综合对比分析2 条理论值曲线总体趋势，可以得出由于改进后的理论值考虑随土体含水率不断变化的基质吸力，并较好的预测了积水点形成时刻，因而其与数值模拟计算值的相对误差更小。并且，降水15 h 后，本文提出的理论模型与数值模拟的结果非常接近，这表明改进的理论模型计算精度更高。

3.2.2 稳定系数

图8 为湿润锋处的稳定系数（Fsf）与饱和层处稳定系数（Fsm）随降雨时间（t）的变化曲线。由图8 可知，稳定系数的变化可分为2 个阶段。

图8 不同位置处边坡稳定系数变化曲线Fig.8 Slope stability coefficient variation curve at different positions

第1 阶段：t＜5 h，此时Fsf＜Fsm，湿润锋处稳定系数更小，坡体在此处偏于不安全。若土体的抗剪强度较小，湿润锋处极有可能转化为滑动面。这是由于降雨初期，分层假设下饱和带土体厚度较小，此时处于降雨入渗第1 阶段（降雨强度控制阶段），雨水全部渗入土体，且坡体饱和层内渗透力较小。

第2 阶段：t＞5 h，此时Fsf＞Fsm，潜在滑动面为饱和层面，主要是由于降雨后期，分层假设下饱和带土体抗剪强度比湿润锋处低；随着饱和带土体厚度不断发展，坡体饱和层内产生的平行于坡表的渗透力也在逐渐发展，导致非饱和土边坡发生平行于边坡表面的较深层滑坡时，往往在饱和层面处发生滑动。

降雨5.5 h 时，湿润锋到达土层交界面，此时Fsf出现明显波动。结合文献[7]可知，当雨水入渗到土层交界面并渗入风化土后，交界面土体体积含水率增长较快，土体抗剪强度迅速减小，且此时需考虑风化土（第2 层土）的土体性质，导致Fsf出现明显的波动。

降雨6.5 h 时，Fsm出现陡降，随后继续相对平缓的下降。这主要是由于随着降雨历时的增加（7 h 左右），雨水在分界面处聚集，形成积水点，导致此时该处土体体积含水率增长速度较快，土体抗剪强度迅速减小且基质吸力消失，甚至产生于平行于坡表的渗透力，进而导致Fsm陡降。

对比Fsf与Fsm2 条曲线发展规律可知：当t＜5 h时，湿润锋面处稳定系数更小，为潜在滑动面；而当t＞5 h 时，模型则以饱和层面为潜在滑动面；即计算边坡稳定性系数时边坡不安全面的相对位置会随降雨历时改变。相较于文献[7]中分析边坡稳定性时仅以湿润锋处为潜在滑动面位置，本文所提边坡稳定性评价方法更为全面。

4 结论

（1）土体中基质吸力对雨水入渗深度的发展具有重要影响。在考虑基质吸力随降雨入渗过程不断变化情况下提出的多层非饱和土边坡雨水入渗深度的分析方法更好的反映了多层结构土层边坡降雨入渗的过程，得到的理论计算结果与数值模拟结果更加吻合。

（2）在降雨入渗过程中，随着降雨入渗深度的增加，湿润锋处的稳定系数与饱和层处稳定系数不断降低，湿润锋到达土层交界面时，湿润锋处的稳定系数出现明显的波动，积水点在土层交界面形成时，饱和层处稳定系数出现陡降。表明土体的体积含水率随着雨水到达土层交界面时迅速增大，甚至产生平行于坡面的渗流，黏聚力与内摩擦角降低，土体抗剪强度迅速下降。

（3）潜在滑动面相对位置随降雨历时的增长而改变，降雨初期，湿润锋处稳定系数相对更小，若土体抗剪强度较小或降雨强度较大则此时湿润锋处极有可能转化为潜在滑动面，随着降雨历时的增长，潜在滑动面转移到饱和层面处。