直接驱动型光栅单色仪的波长标定

李香香，牛海波，刘会玲，竹有章

（1.西安交通大学城市学院 护理系，西安 710018；2.西安交通大学城市学院 物理系，西安 710018）

光谱测量与分析已广泛应用于物理、化学、材料、生物医学等科研领域，以及环境监测和产品质量检测等生产生活领域，常见的有吸收光谱、荧光光谱、拉曼光谱等[1-6]。单色仪是各种光谱测量设备不可缺少的核心组件，其功能是利用色散元件把复色光分解为准单色光。使用最多的是光栅单色仪，具有光谱范围宽、色散均匀、波长分辨率高等优点。要想精确的测量光谱，有必要需要熟悉设备的原理并能够正确使用和维护。单色仪的标定对于光谱测量尤为重要，直接影响后续测量的可靠性。虽然是传统设备，近年来仍有文献不断报道这方面的工作，文献[7-9]先后报道了用连续谱光源对单色仪进行标定的方案，以解决汞灯等线状谱光源取样点不足的问题；文献[10]采用激光多级衍射线法在可见红外的宽光谱范围内讨论了单色仪的标定精度；文献[11]系统讨论了狭缝宽度对单色仪标定结果的影响。

在讨论单色仪波长标定的文献中，大多基于带有“正弦装置”的单色仪[12-14]，所谓正弦装置是指通过机械装置把匀速直线运动转化为按正弦规律转动。随着科技的进步和发展，光栅单色仪也在不断革新之中。当前用步进电机直接驱动光栅按所需规律转动已非常容易，因此现代单色仪大多去除了正弦装置，有必要对这类单色仪波长标定进行讨论。另一方面，文献中关于单色仪波长的标定大多采用数据拟合的方法建立单色仪指示波长和真实波长之间的关系，拟合参数不具备真实的物理意义且在偏离取样点的地方可能存在较大误差[13-15]。本文从光栅衍射方程出发，对当前主流的步进电机直接驱动的光栅单色仪的波长标定方法进行了系统讨论，仅依据仪器硬件参数计算单色仪输出波长和电机转动步数的关系，不包含任何拟合过程。经实验检验，标定结果在很大波长范围内具有非常高的精度。本工作对于使用光谱测量设备的研究人员和实验技术人员有一定参考价值。

1 光栅单色仪的基本原理

光栅单色仪是基于光栅衍射现象将复色光分解为单色光的光学仪器，其结构不尽相同，但基本原理是一致的。使用最为广泛的是Czerny-Turner 型单色仪，如图1所示。

从入口狭缝进入的光经凹面镜1 准直后照射在光栅上，经光栅衍射后某一波长的光经凹面镜2聚焦后透过出口狭缝形成准单色光。通过转动光栅可以改变输出波长，具体定量关系可以从光栅衍射方程出发进行计算。平面光栅衍射方程如式（1）所示：

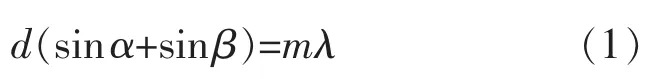
式中：d 为光栅常数，也可以用刻线密度n 来表示，即d=1/n；α 和β 分别是相对于光栅法线的入射角和衍射角，在式（1）中定义入射角α 为正值，β 和α 位于法线同侧时为正，反之为负；m 为衍射级数，单色仪通常取一级衍射，即m=1；λ 为衍射角β 对应的波长。因此光栅衍射方程可具体写为

式中：波长λ 的单位为nm；n 为每毫米的刻线数，因单位换算引入一个系数。

对于一台确定的单色仪，当光栅转动时α 和β都变化，但是α-β＝2K 为恒定值（图1中β 为负），即入射角和衍射角之和为恒定值。2K 在此称为单色仪光轴夹角，由仪器的硬件结构决定。再定义一个转动角ϕ为光栅法线转过的角度，在ϕ=0 时α＝-β＝K。由图1中的几何关系不难得出：

把式（3）带入式（2）可得：

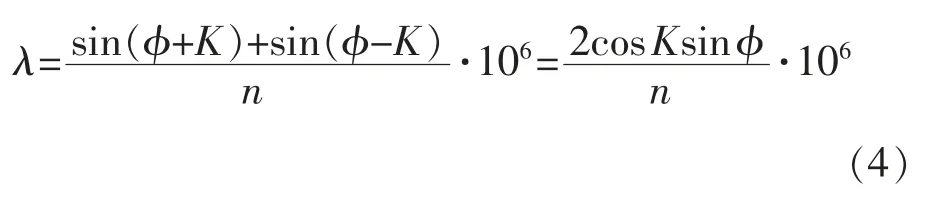
式中：K 和n 为设备硬件参数，输出波长λ 由光栅转角ϕ唯一确定，两者之间是正弦关系。这就是光栅单色仪波长标定的理论依据。

2 光栅单色仪波长标定

在光谱测量时需要波长按照等间距扫描，根据式（4）则光栅的转动一定是非均匀的。为了解决非均匀转动的复杂性，早期的单色仪普遍采用正弦装置来解决这一问题，即通过机械装置把匀速运动转化为按正弦规律转动。随着电子技术的进步和仪器自动化水平的提高，用步进电机直接驱动光栅按所需规律转动已非常容易，因此现代单色仪已去除了正弦装置，也避免了由此引入的误差。

单色仪中的光栅安装在光栅转台上，转台通过传动齿轮在步进电机的驱动下转动，如图1左侧插图所示。步进电机每收到一个脉冲信号转动一个恒定的角度，如在16 细分情况下基本步长1.8°的步进电机转一圈需要3200 步。电机转轴和光栅转台之间通过齿轮传动，电机转一圈光栅转台只转过一个小角度，如某型号单色仪电机转一圈光栅转台仅转动2°，用上述电机驱动则光栅转台转一圈需要576000 步，控制精度非常高。通过记录步进电机转动的步数，就可以准确判断转过的角度。绝对转动量的标定需要一个参考点作为零点，光栅转台的机械零点由安装在转台和电机轴上的两个光电位置传感器获得，单色仪在初始化过程中会自动找到机械零点。每一块光栅还有一个零点，即式（4）中ϕ=0的位置，也就是输出波长为零的位置。两个零点之间相差一个固定的步数，表示为N0，其它波长对应的转动步数可表示为

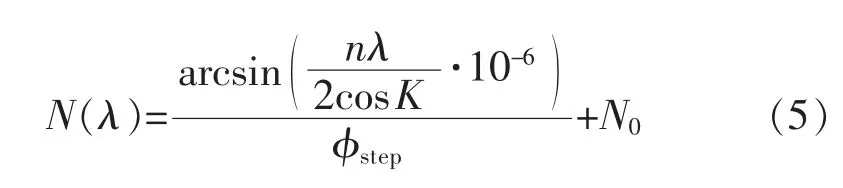
式中：ϕstep表示光栅步距角，即电机转动一步光栅转动的角度。如果一个圆周被分为576000 步，则ϕstep＝2π/576000。因为步距角非常小，式中第一项取整产生的误差通常可以忽略。只要确定了N0，带入硬件参数K 和n 即可求得任意波长对应的转动步数。

3 实验验证与讨论

在一套自行搭建的系统上对上述理论分析结果进行了实验验证。所用单色仪光轴夹角K=17.2°，光栅刻线密度n=1200/mm，焦距为300 mm，出口及入口狭缝宽度均设为200 μm，光栅转动的步距角为ϕstep=2π/576000。采用汞灯作为光源，光电倍增管作为探测器，通过单光子计数器进行信号处理。由自编Labview 程序控制单色仪中步进电机的转动和光强数据的读取和记录。按照式（5）标定单色仪首先要确定光栅零点N0，根据定义光栅位于零点时入射角等于衍射角，此时单色仪输出零级衍射光，在光谱上表现为一个强的峰值。实验中通过在零级衍射峰附近的扫描，取零级衍射峰中心对应的步数作为光栅零点。然后严格按照式（5）计算即可得到输出任意波长电机所需转动步数。

如图2所示，对汞灯光谱的测试结果如图2中实线所示，在300～900 nm 范围内得到的一系列线状谱，其峰值已标注在图中。所测得峰值和标准值完全一直，其中大于700 nm 三个峰分别是365.0 nm，404.7 nm，435.8 nm 光的二级衍射峰，测得的波长恰好是其2 倍。这一结果充分验证了该标定方法的可行性和准确性。

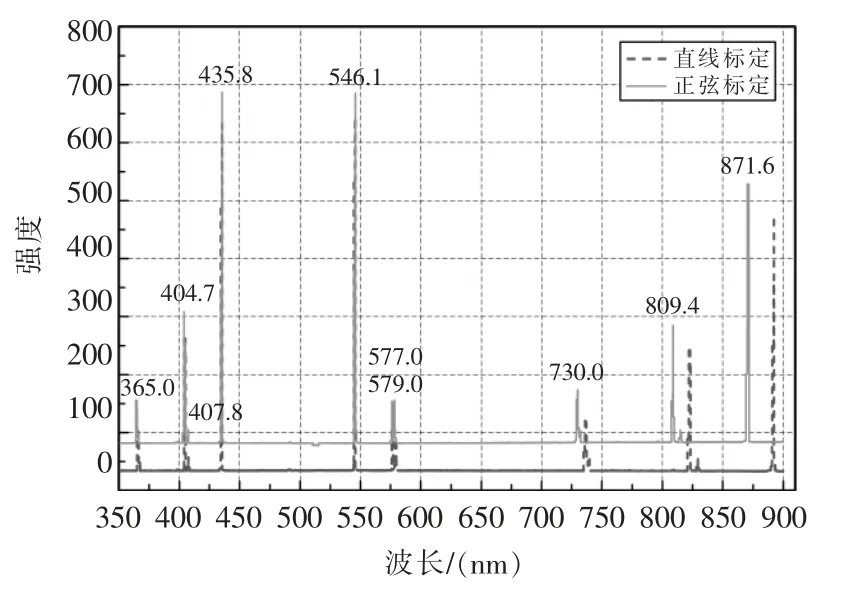
图2 正弦（实线）和线性（虚线）标定情况下测得的汞灯光谱Fig.2 Spectra of mercury lamp under the condition of sine（solid） and linear（dashed） calibration

本标定方法的特点在于不包含任何拟合过程，完全依据硬件参数计算出单色仪输出波长和步进电机转动步数的对应关系。对于光栅零点的确定采用了零级衍射光，因此使用任何光源都可以，无论是现状谱还是连续谱。在实际中，有些仪器为了简化控制，将式（5）简化为线性关系N（λ）＝Dλ+N0′。为了进行对比，对同一台单色仪按照线性关系进行了标定，标定时对汞灯365.0 nm，404.7 nm，435.8 nm，546.1 nm，579.0 nm 五条主要谱线进行了线性拟合。

线性标定的测量结果如图2中虚线所示，可以看出在大约400～600 nm 范围内线性标定测量的光谱和标准值具有较好的一致性，但是超出该范围则具有明显差异，特别是在大于700 nm 的区域。其原因是直线可以看作正弦曲线的切线，在一定范围内两者一致性较好（特别是在小角度时）。以上结果说明在一定光谱范围内，线性标定也有比较好的精度，因此有些商业仪器采用线性标定。也有文献报道采用更复杂的多项式或正弦函数拟合进行单色仪波长标定[13-15]，其效果肯定比线性标定好，但是在偏离取样点或超出取样范围后容易产生较大误差，特别是在对精度要求非常高的情况下。本文采用的方法不包含任何拟合过程，理论上在整个机械扫描范围内都具有很高的精度。此外，单色仪在使用一段时间后因机械磨损等原因需要进行校准。本文所述方法各硬件参数不会发生变化，只有光栅零点可能发生飘移，这时可以使用零级衍射峰或其它任意已知波长的激光进行校准，操作非常容易。而采用其它复杂的拟合方法进行标定的单色仪校准则比较麻烦。

如果因某些原因无法获得单色仪的光轴夹角K和步距角ϕstep，比如要把一台按照线性标定的单色仪改为正弦标定，经常不知道这两个参数。这种情况下也可以通过一定方式获得这两个参数。步距角ϕstep由步进电机和传动装置决定，步进电机转一圈的步数为某个特定整数（如1600，3200，6400 等），传动比可以通过数齿轮齿数确定（如90，180 等），也是某一整数，两个的乘积只能是一些特定整数。打开单色仪盖子，通过记录转过特定角度所需步数可以换算出光栅转动一圈所需步数的初步数值，其精确值一定是推算的一系列特定整数中最接近该数据的那一个，即可得到步距角ϕstep。光轴夹角K 可以通过对包含一组线状谱的标准光源（如高压汞灯）的测量进行探寻。K 值一般在几度到十几度范围内，如果所给K 值偏小，则所测波长大于标准值且波长越长偏差越大；反之亦然。通过多次尝试就可以精确获得K 值。如果各波长和标准值有恒定偏差，则是由光栅零点N0不准确引起。如果一台单色仪内安装有多个光栅，则应逐个标定。每一块光栅有自己的零点，但光轴夹角K 和步距角ϕstep不变。

以上讨论都是基于单点探测器，单色仪出口安装有狭缝。如果是采用CCD 多通道探测器，以上计算的只是其中心像素的波长，其它像素对应的波长还需要进行标定，在对CCD 进行标定时，光轴夹角K 也是一个重要的参数。

4 结语

光栅单色仪光谱测量的核心器件，在科研、检测等相关领域有非常广泛的应用。针对步进电机直接驱动型单色仪，从最基本的光栅衍射方程出发，推导了单色仪输出波长和电机转动步数的关系。所得关系仅依赖于单色仪硬件参数，不包含任何拟合过程。在一台单色仪上进行了实验验证并与线性标定等方法进行了比较，该方法在从紫外到近红外范围内均能得到准确的波长输出，具有很好的实用性、准确性和便捷性。讨论了在未知情况下获取单色仪硬件参数的方法。对于使用相关设备的科研和实验技术人员以及仪器开发人员具有一定的帮助。