基于滑模控制的光伏并网逆变器控制策略
2022-11-23高兰香赵兴勇宋玲燕王雨祺
高兰香,赵兴勇,宋玲燕,王雨祺
(山西大学 电力与建筑学院,太原 030013)
并网逆变器作为光伏(PV)并网系统的核心设备,它的性能与整个系统的运行效率息息相关[1]。文献[2]采用PI 控制使系统动态性能达标,但并网电流THD 较大,且当受到外界因素和不确定性的影响时,难以保证其鲁棒性和稳定性。文献[3]将滑模控制(SMC)应用于光伏并网逆变器,控制性能明显优于PI 控制,并将指数趋近律中的符号函数换为饱和函数来减弱抖振,但它是不连续函数,不能进行求导。文献[4]在电机控制中,设计了一种趋近律,引入变速项,且切换函数采用双曲正切函数,使之连续化,减弱了系统抖振,但未实现全局鲁棒。文献[5]在电机调速系统中,选取误差及其积分构造滑模面,有效消除了稳态误差,选取合适的积分项初值,使系统在一开始就处于滑动阶段,从而使整个运动过程都具有鲁棒性。
高阶滑模控制由于其简单、鲁棒性好、能有效抑制抖振等特点,是目前解决滑模抖振的一种新的控制手段[6]。文献[7]在光伏系统的MPPT 中,采用了超螺旋滑模控制(STC),不仅实现最大功率跟踪,而且将不连续的符号函数转移到高阶导数,使输出的控制量连续从而达到消除抖振的目的。
综上,本文综合考虑鲁棒性与稳定性,提出一种针对LCL 型光伏并网逆变器的改进型双闭环滑模控制策略(以下用“改进型SMC”代替)。首先,选取误差及其积分构造滑模面,消除稳态误差,使系统实现全局鲁棒。其次,电压环结合变指数趋近律设计滑模控制;电流环采用STC,并采用有源阻尼抑制谐振;利用Lyapunov 函数证明了系统的稳定性。最后,通过仿真分析,验证了所提出方法的有效性。
1 三相光伏并网逆变器拓扑结构及数学模型
系统结构如图1所示。图中,D 为二极管;iPV为光伏输出电流;iC为电容电流;iinv为流入逆变器的电流;Cdc为直流侧电容;V0~V6为IGBT 开关管;L1为逆变器侧电感;C 为滤波电容;L2为电网侧电感;R1和R2分别为电感L1和L2的寄生电阻;ug为网侧电压。
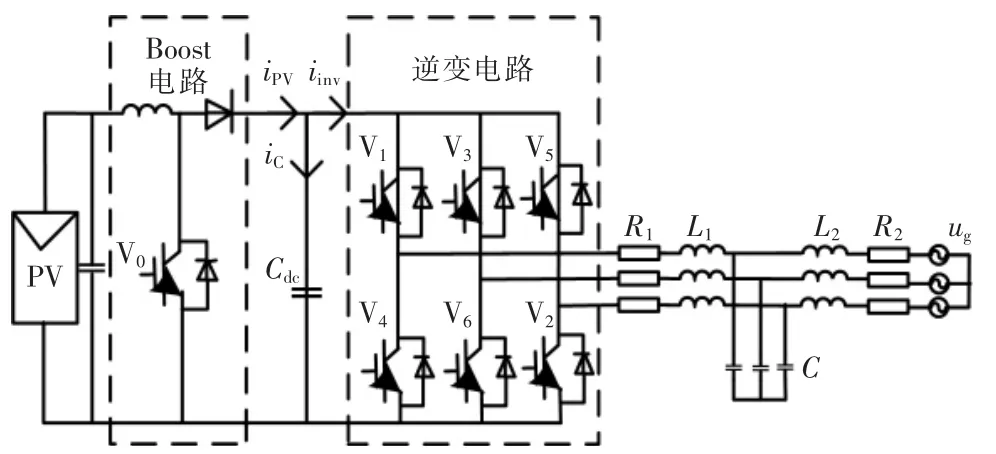
图1 LCL 型三相光伏逆变并网系统结构图Fig.1 Structure diagram of LCL three-phase photovoltaic inverter grid-connected system
PV 并网逆变器在dq 坐标系下的状态方程如式(1)所示:
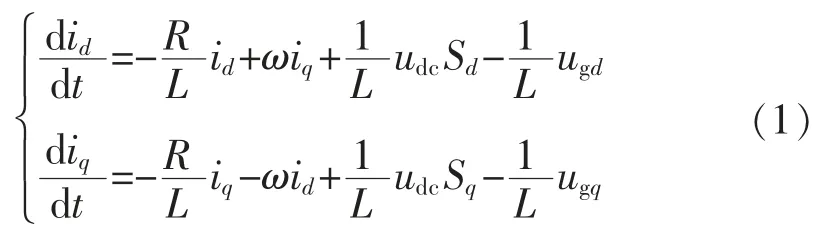
式中:L=L1+L2;R=R1+R2;udc为直流侧电容器两端电压;id,iq,ugd,ugq,Sd,Sq为网侧电流、网侧电压、开关函数在d,q 轴上的分量。
网侧的有功功率和无功功率分别为

式中:Pg为有功功率;Qg为无功功率。
考虑逆变器在理想的dq 坐标下,电网电压ugq=0,则电流的d 轴分量igd可以调节Pg,电流的q 轴分量igq可以调节Qg。忽略逆变器的能量损耗,可得到功率平衡方程为
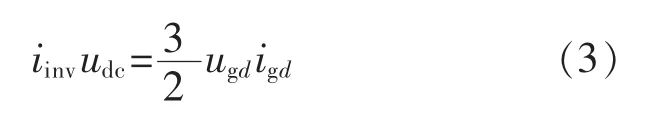
根据式(3),由KCL 可得:
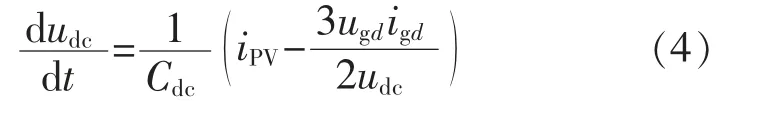
2 改进趋近律设计
2.1 传统指数趋近律
文献[8]中提出了趋近律的概念,并设计了一种指数趋近律,被广泛应用。其表达式为
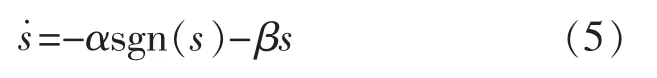
式中:s 为滑模面函数;α,β 为增益参数,且大于零。
由式(5)可以看出,传统指数趋近律中含有高频切换不连续项αsgn(s),由于αsgn(s)的存在导致控制输入不连续,这是产生抖振的主要原因。
2.2 变指数趋近律
文中提出一种变指数趋近律,削弱指数趋近律
中存在的抖振。其表达式为
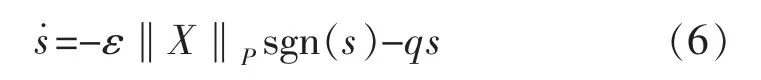
式中:‖X‖P为变量X 的p 阶范数;ε,q 为增益参数,且大于零。
该趋近律由两项组成,-ε‖X‖Psgn(s)为变速项,-qs 为指数项。初始时刻,状态变量距离滑模面较远(即趋近运动),系统是以变速和指数2 种速率运动,系统的速度随‖X‖P增大而增大,系统到达滑模面时间缩短;状态变量接近滑模面(即滑动运动),-qs 逐渐减小直至为0,此时变速项占主导地位,系统的速度随‖X‖P减小而减小,直至为0,即sgn(s)的系数为0,抖振得到抑制。
为了进一步抑制抖振,对sgn(s)进行平滑化处理,用双曲正切函数代替,其表达式为
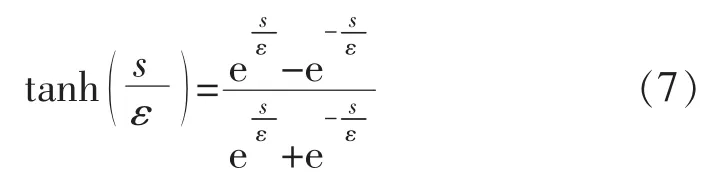
相比sgn(s),它是一个在(-1~1)之间变化的连续函数,且斜率可以随着常数ε 的大小而变化。ε 越大,斜率越小,曲线越平滑;ε 越大,曲线越接近sgn(s)。
2.3 超螺旋算法
STC 是一种结合超螺旋算法(super-twisting)设计的二阶滑模控制。其表达式为
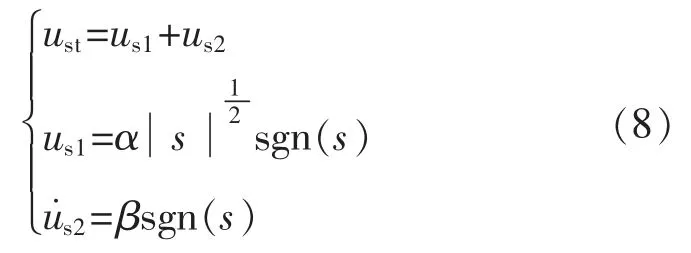
由式(8)可以看出,super-twisting 包括2 个部分,第一部分us1是一个连续的滑模面函数,第二部分us2是在时间上对滑模面积分,将sgn(s)由u 转移到u 的一阶导中,不再直接影响控制律u,使输出的控制信号连续,从而抑制抖振。
3 控制策略分析
控制模型如图2所示。将检测到的三相并网电流ia,ib,ic经过park 变换得到电流在dq 轴上的分量id和iq,d 轴的参考值i*d为电压外环经过SMC 的输出信号,令q 轴的参考值i*q为0,使并网时的功率因数为1。电流误差经电流内环的STC 得到电压信号ud,uq,经反Park,Clark 变换得到电压在α,β 轴上的分量uα,uβ,同时引进滤波电容电流的反馈,并采用SVPWM 调制。
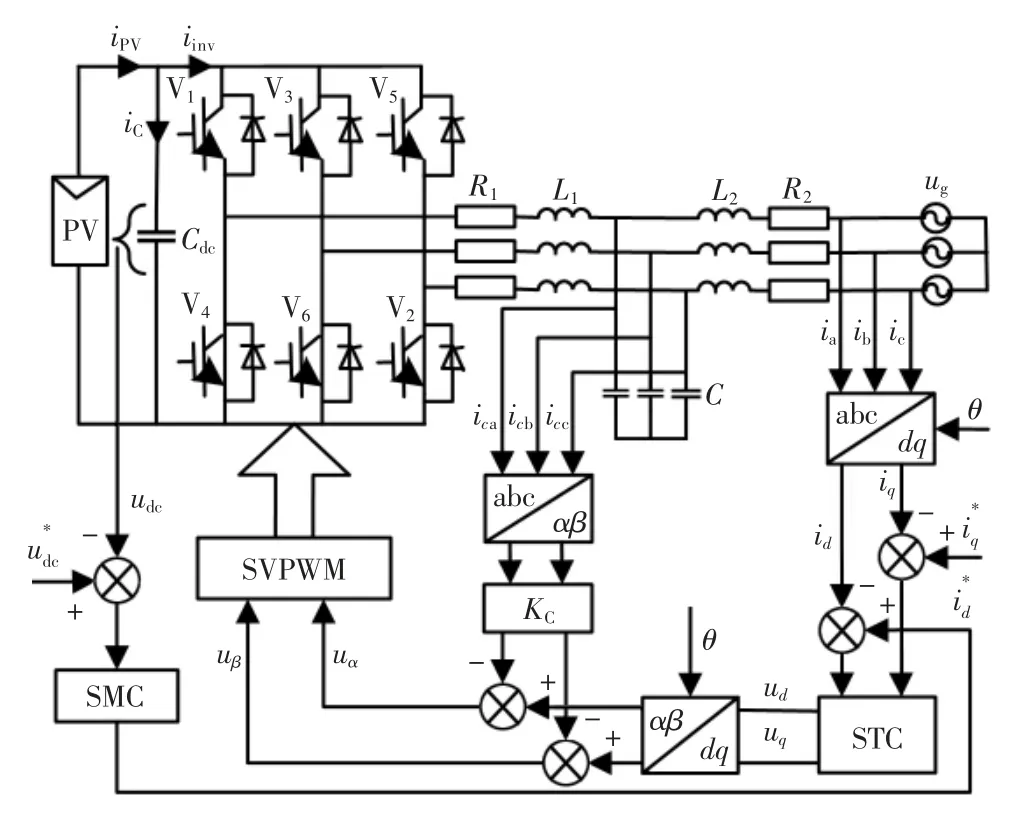
图2 光伏并网系统控制框图Fig.2 Control model diagram of photovoltaic grid-connected system
3.1 电压外环滑模控制器设计
定义电压跟踪误差为

选取误差及其积分构造滑模面,其表达式为

若选取合适的积分初值,可使系统直接在滑动阶段运动,具有全局鲁棒性。选取积分初值为

式中:λ 为增益系数,且λ>0;e(0)表示误差在零时刻的值。
结合式(4),对式(10)求导可得:
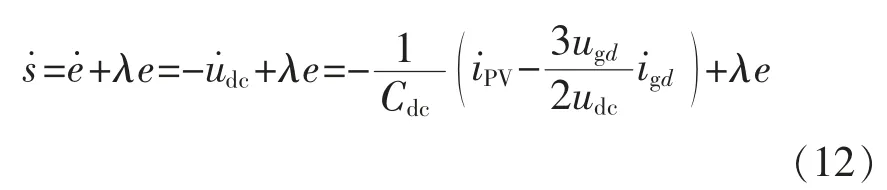
联立式(6)、式(7)和式(12),可得电压外环的控制方程为
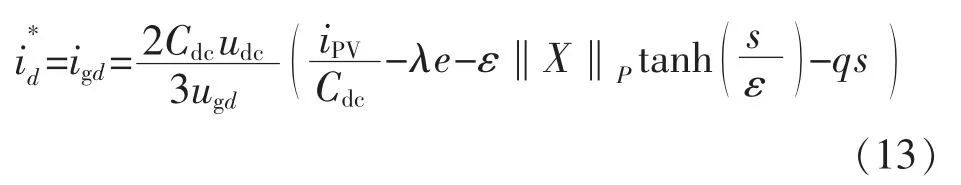
定义Lyapunov 函数为V=0.5s2,对其求导得:
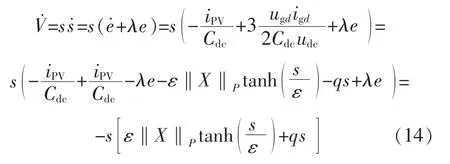
3.2 电流内环滑模控制器设计
定义电流误差为

设计积分滑模面为
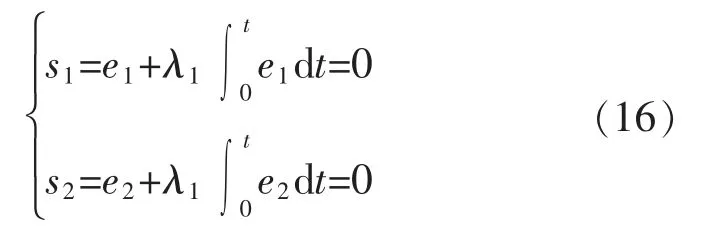
式中:λ1为控制增益,且大于零。
选取积分初值为

选取控制律为等效控制结合超螺旋算法,故式(1)中的Sd,Sq可表示为

结合式(1),对式(16)求导,可得:

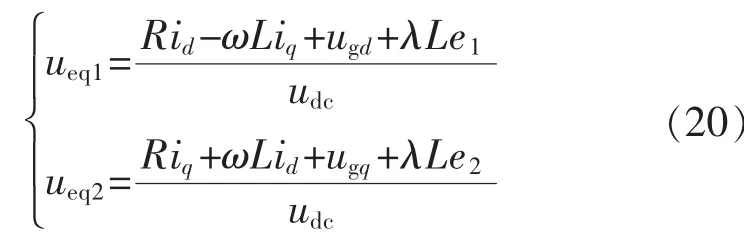
结合式(8)、式(18)和式(20),可得电流内环的控制方程为
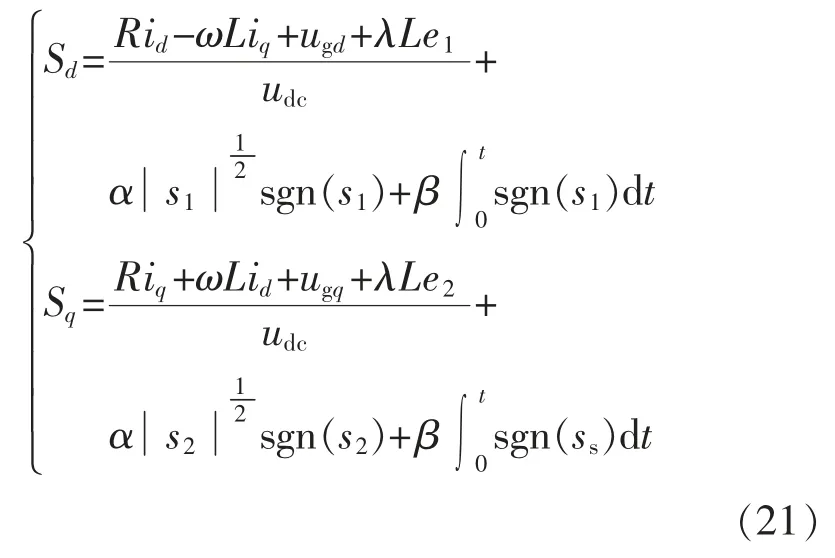
其中,ud=udcSd,uq=udcSq。将2 个控制变量ud和uq经反Park,Clark 变换得到电压在α,β 轴上的分量uα,uβ,同时引进滤波电容电流的反馈,最终通过SVPWM 得到逆变器的控制脉冲信号。
定义Lyapunov 函数为V=0.5sTs,对其求导得:

4 仿真及结果分析
根据第3 节设计的电压、电流环滑模控制器,在Matlab/Simulink 仿真平台搭建模型,逆变器分别采用PI 控制、基于传统指数趋近律的滑模控制(以下用“传统SMC”代替)和改进型SMC。系统主要参数为直流侧参考电压=800 V,三相电网电压有效值为220 V,逆变器侧电感L1=2 mH,滤波电容C=50 μF,电网侧电感L2=0.01 mH。
4.1 抖振仿真对比实验
图3为传统指数趋近律与变指数趋近律、STC控制律的对比图。
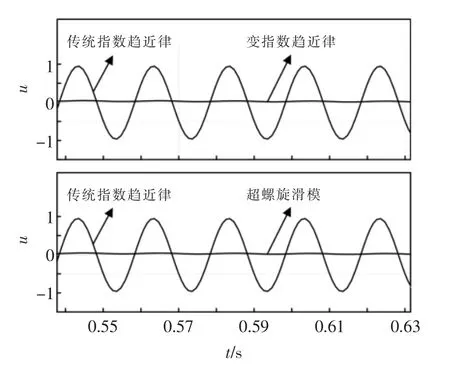
图3 趋近律对比Fig.3 Comparison of approach law
从图3可以看出,传统指数控制律因sgn(s)的存在,出现抖振。而变指数趋近律中sgn(s)的增益参数为0,抖振得到抑制;STC 控制律将sgn(s)放到一阶导数中,不再直接影响控制律u,使输出的控制信号连续,从而抑制抖振。
4.2 系统控制性能对比实验
工况1:理想电网条件。对3 种控制下A 相并网电流进行谐波分析。图4为改进型SMC 下A 相并网电压与电流波形,图5为并网电流谐波分析图,表1为电流谐波畸变率对比。

图4 改进型SMC 下A 相并网电压与电流波形Fig.4 Waveform of A-phase grid-connected voltage and current under improved SMC
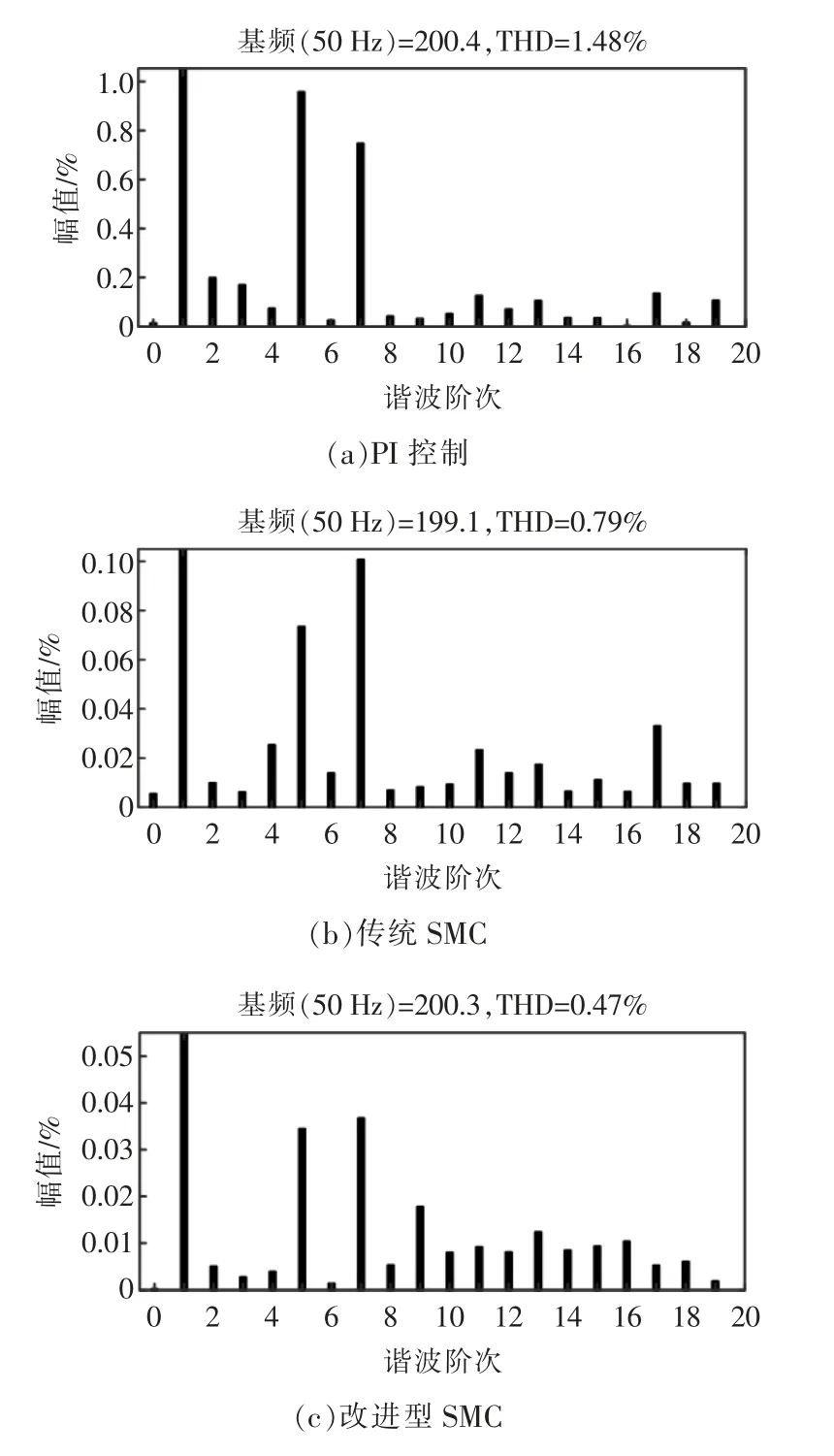
图5 3 种控制下并网电流谐波分析Fig.5 Harmonic analysis of grid-connected current under three kinds of control

表1 并网电流谐波畸变率对比Tab.1 Comparison of harmonic distortion rates of grid-connected current
由图4可得,改进型SMC 下并网电流在半个周期内就到达稳定状态,与电网电压频率、相位保持一致,符合入网要求;由图5及表1可得,改进型SMC 下并网电流谐波畸变率明显减少,输出质量得到很大改善,更加有利于系统稳定运行。
工况2:系统参数(网侧电感值)变化。在0.3 s时将网侧电感值由0.01 mH 变为0.005 mH。图6为3 种控制下A 相的并网电流及系统无功功率波形;图7为并网电流谐波分析图,表2为电流谐波畸变率对比。
由图6、图7和表2可得,当网侧电感值发生变化后,PI 控制下的电网电流发生明显畸变,无功功率有很大波动,且电流THD 大于5%,不符合标准要求;传统SMC 和改进型SMC 下电网电流和无功功率几乎无波动,但改进型SMC 下电流谐波畸变率更小,波形更光滑。由此可见,改进型SMC 对系统参数改变并不敏感,具有较强的鲁棒性。
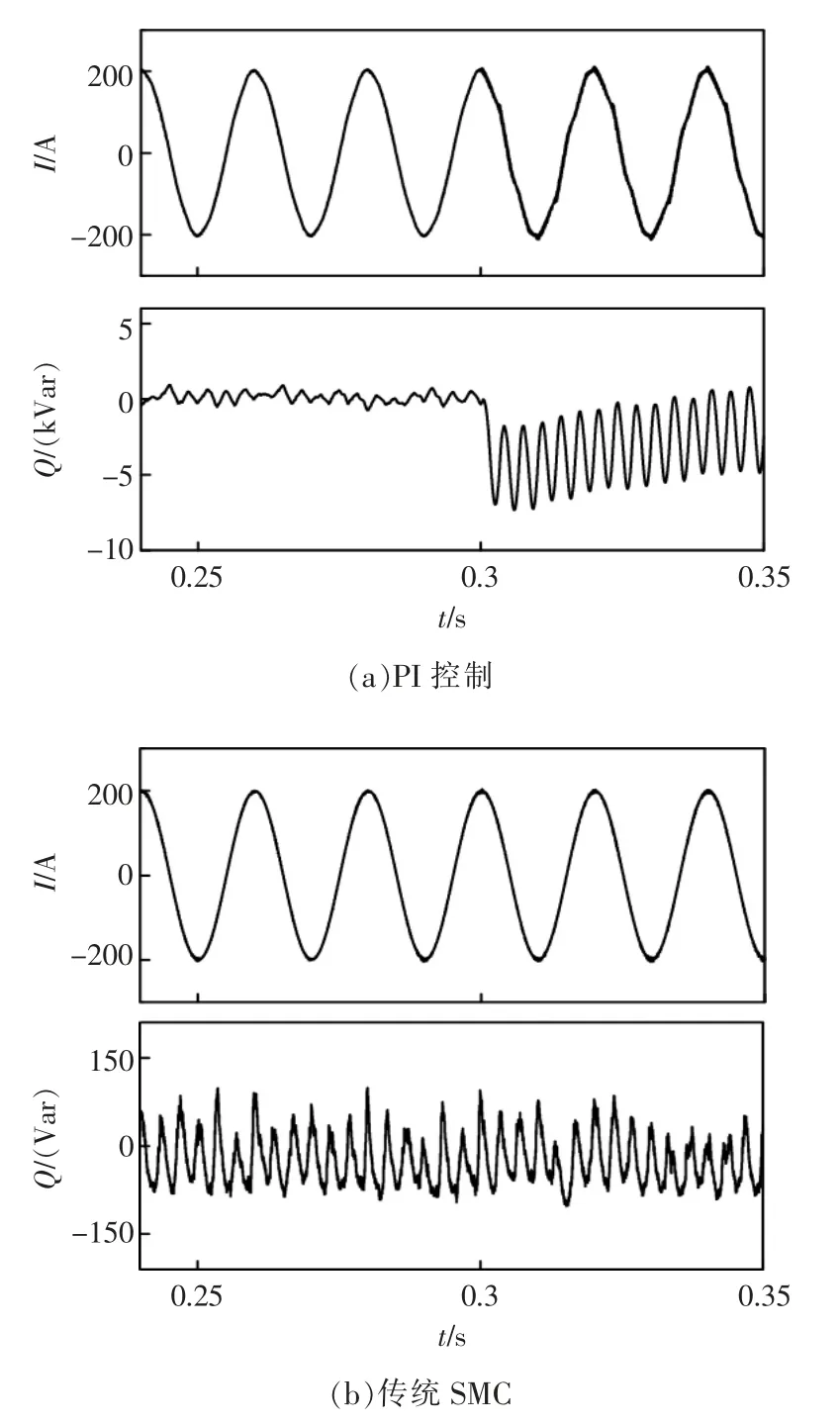

图6 改变网侧电感后A 相并网电流及系统无功功率Fig.6 A-phase grid-connected current and system reactive power after changing the inductance on the grid side
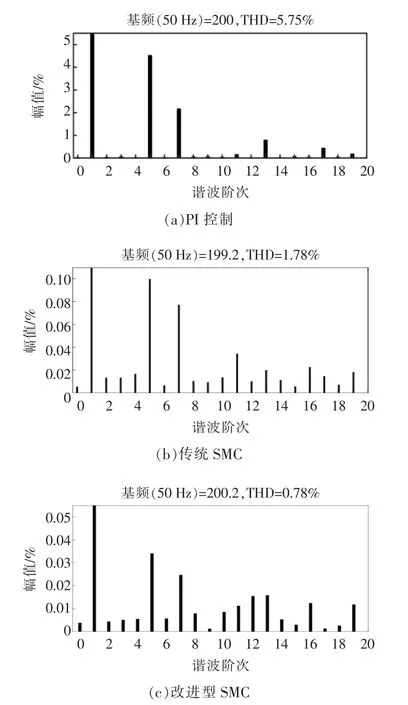
图7 并网电流谐波分析Fig.7 Harmonic analysis of grid-connected current
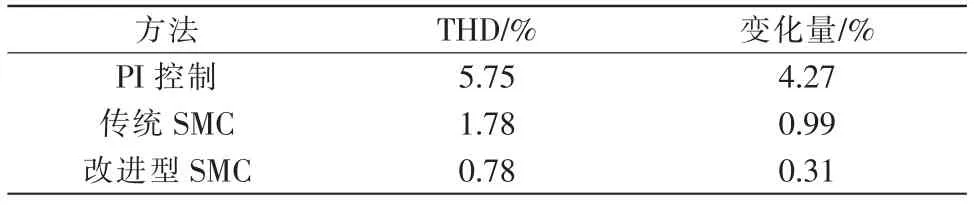
表2 并网电流谐波畸变率对比(改变网侧电感)Tab.2 Comparison of grid-connected current distortion rate(change of grid-side inductance)
工况3:保持温度为25 ℃不变,光照强度在0.5 s时由800 W/m2升为1000 W/m2。图8为3 种控制下直流母线电压波形,表3为直流母线电压动态性能对比。
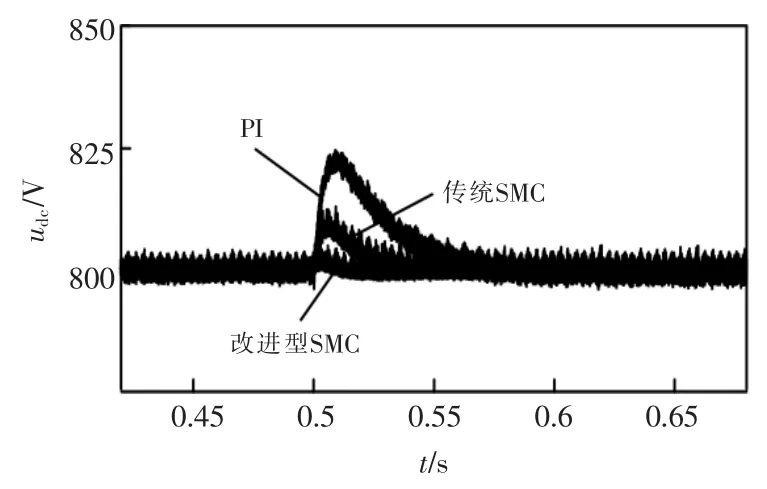
图8 直流母线电压波形Fig.8 DC bus voltage waveform

表3 直流母线电压动态性能对比Tab.3 DC bus voltage dynamic performance comparison
由图8和表3可得,改进型SMC 调节时间最短,超调量最小。当光照强度突变时,采用改进型SMC 可在提高动态响应的同时有效降低直流母线电压过调。
5 结语
本文提出一种改进型双闭环滑模控制策略,通过理论推导和算例分析,主要得出以下结论:
(1)通过选取误差及其误差积分构造滑模面,消除稳态误差,克服了传统SMC 只在滑动模态有鲁棒性的缺陷,使系统在整个过程中具有鲁棒性。电压外环控制采用变指数趋近律,减弱抖振,使系统的收敛速度得以自适应调节;电流内环控制结合超螺旋算法,对不连续的切换项进行积分,使输出的控制量连续,减弱抖振。
(2)所提的改进型SMC,使系统并网电流质量得到很大改善;在系统参数变化和光照强度改变的情况下,能快速恢复稳定,且波动较小,由此体现了强鲁棒性的特点。
