基于迭代频域能量算子的风电机组转速提取方法
2022-11-23宫永立于保春彭迪康
徐 进,宫永立,于保春,彭迪康
(1.中国绿发投资集团有限公司,北京 100020;2.都城伟业集团有限公司,北京 100020;3.鲁能集团有限公司,北京 100020;4.华北电力大学电站能量传递转换与系统教育部重点实验室,北京 102206)
0 引言
随着风电机组设备趋向于大型化、海洋化,风电机组运行状态监测成为了保障风电机组安全可靠运行的重要支撑技术。风电机组传动系统一般都配置了振动监测系统(CMS),对主轴承、增速齿轮箱、发电机轴承等机械部件进行状态监测。然而,由于风电机组的变风速、变载荷工况特点[1],使得振动信号包含幅值及相位调制现象,影响了状态监测的效果。因此,文献[2],[3]专门强调阶次跟踪是解决转速波动问题最为直接有效的方法。由于阶次跟踪的实施需要与振动信号进行同步采集转速信息,而风电机组现有的转速信号由包含发电机编码器的SCADA系统进行采集[4]。由于SCADA与CMS系统存在时间差和采样频率差异,通过发电机编码器所提供的转速信号对大转速波动情况下振动信号进行阶次跟踪将受到极大影响。为提高振动信号分析效果,通过振动信号本身提取风电机组的瞬时转速(频率)成为了目前的研究重点[5]。根据振动信号提取瞬时转速进行阶次跟踪的优点还在于瞬时转速信息的获取无需额外安置转速编码器,在降低了硬件成本及数据传输、存储成本的同时,保证了通过CMS系统采集的振动信号进行状态监测的可靠性。
通过振动信号本身进行瞬时转速提取主要有两种方法,分别为提取时频脊线和通过对相位解调获取的相位进行微分[6]。其中对于前者,高冠琪[7]提出用同步提取转换的方法来提高时频分析结果的时频分辨率,从而提升瞬时频率估计的准确性。曹书峰[8]将Wigner-Ville分布与小波尺度谱进行融合,之后用峰值搜索提取时频脊线,有效地提取出振动信号的瞬时频率。以上方法均选取一个感兴趣的振动成分并提取其时频脊线来进行瞬时频率估计,而部分场合由于噪声以及传递函数的影响,选取单一的时频脊线估计瞬时频率容易出现较大的误差,因此文献[9]提出了一种概率融合,提取短时傅里叶变换中多个振动成分的时频脊线并进行多阶次加权平均来估计瞬时频率的多阶次概率加权法(MOPA)。
任锦盛通过Hilbert变换窄带解调估计出风电机组10 s瞬时转速,并进行后续角度域同步平均分析。Coats M D[10]提出了一种通过Hilbert变换进行迭代相位解调的瞬时频率估计方法,相较于未迭代的窄带解调瞬时频率估计方法,该方法能够更有效地提取感兴趣的振动成分的瞬时频率并通过其进行阶次跟踪,提高了故障诊断的准确度。Antoniadou I[11]论述了风力涡轮机齿轮箱在不同运行条件下的状态监测。通常齿轮箱系统是非线性的,目前已开发了简化的非线性齿轮模型,在此基础上首次应用提出的时频分析方法,在模拟中及实际风力涡轮机齿轮箱实验数据中检验了不同负载的影响。
为对风电机组传动系统振动信号的瞬时频率进行精确的估计,本文提出了一种基于迭代频域能量算子(IFDEO)方法来处理大波动变转速风电机组振动信号,并通过实测数据对风电机组进行验证。验证结果表明,尽管风电机组实测数据的振动成分复杂,但通过IFDEO进行迭代更新瞬时频率并进行阶次跟踪能够将高阶振动成分与其边频带进行有效地分离,在此基础上进行进一步的信号处理能够有效地识别风电机组传动系统的故障。
1 迭代频域能量算子
1.1 Teager Kaiser能量算子及频域能量算子
Teager Kaiser能量算子对于一个一维连续信号x(t)在时域上的定义为

式中:x˙(t),x¨(t)分别为信号x(t)相对于时间的一阶和二阶导数。
给定一个幅值和频率调制的单分量信号,则:
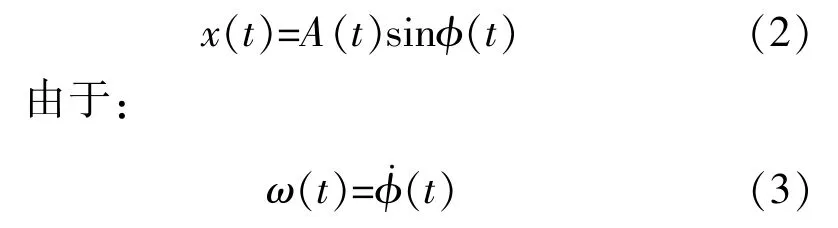
因此,通过Teager Kaiser能量算子对其进行解调的瞬时频率和瞬时幅值分别为


Teager Kaiser能量算子近似等于信号x(t)的一阶导数的平方包络。因此可以通过频域计算求信号x(t)的Teager Kaiser能量算子(频率能量算子),即通过对信号x(t)在频域上与jω进行相乘,即可获得x(t)的一阶导数x˙(t),并通过获取其平方包络获得信号x(t)的频域能量算子。
以此可推导出信号x(t)通过频域能量算子计算的瞬时频率为

即通过计算x(t)与x˙(t)的平方包络并相除以获得信号x(t)瞬时频率的平方。相较于直接通过Teager Kaiser能量算子进行解调获取ω(t)[式(4)],通过式(11)进行瞬时频率获取的优点在于避免了Teager Kaiser能量算子的因果性(滤波器在低频和高频截止频率附近有相移,并且在通带外的滚降系数较大)。
1.2 迭代瞬时频率估计
由于频率能量算子进行相位解调获取信号的瞬时频率需要单分量信号,因此为降低频率混叠的影响,选取的振动成分一般应为低阶频率成分,并对其进行窄带解调。假设一阶振动成分的频率为O且转速波动为±W%,则其在频谱上的带宽为(1±W%)O。
因此其高阶谐波(kO)的带宽为(1±W%)kO。
如选取一阶振动成分进行瞬时频率估计,转速波动应限制在±33%以内,以保证一、二阶振动成分在频域内能够有效地分离。
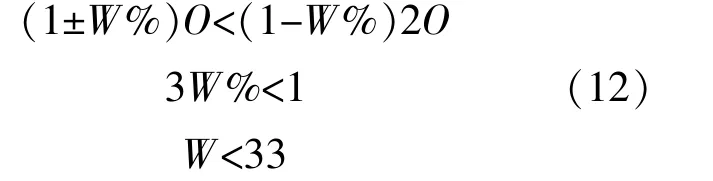
选取更高阶的振动成分进行瞬时频率估计将导致转速波动更为有限。如选取二阶振动成分进行瞬时频率估计的转速波动将限制在±20%以内,而选取三阶振动成分进行瞬时频率估计的转速波动将限制在±14.3%以内。
尽管通过提取低阶振动成分进行瞬时频率估计并进行阶次跟踪能够降低绝大部分转速波动造成的频率混叠的影响,使得绝大部分振动成分与其倍频在阶次谱上不再混叠。由于低阶振动成分转速波动缓慢,因此通过低阶振动成分进行瞬时频率估计仍会产生较大的误差,使得高阶振动成分极易与其边频带混叠在一起,降低了故障诊断的准确度。因此,可以通过选取阶次跟踪后的角度域振动信号中更高阶的振动成分进行进一步的瞬时频率估计,并进行迭代阶次跟踪,通过提高瞬时频率精确度以实现细化阶次谱的目的。本文提出的通过IFDEO进行振动信号无键相阶次跟踪的流程如图1所示。
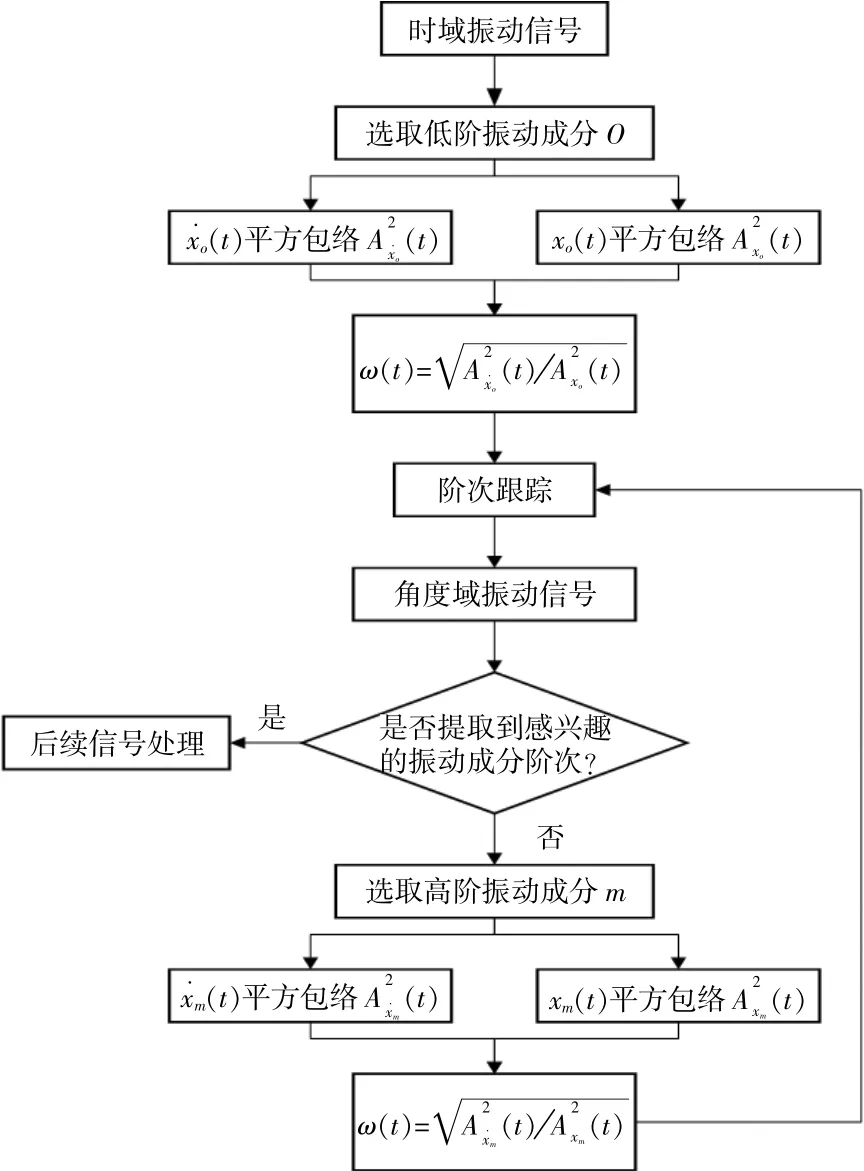
图1 通过IFDEO进行阶次跟踪流程Fig.1 Flowchart of order tracking method using IFDEO
在进行阶次跟踪后的角度域振动信号可进行后续的包络分析或更进一步的信号处理以实现故障诊断的目的。
2 结果
通过便携式多通道风电数据采集系统以12.8 kHz在某风场采集了2台1.5 MW机组齿轮箱的加速度信号,齿轮箱传动比为94.995。加速度传感器安置于低速轴后轴承,灵敏度为100 mV/g,同时在高速轴安置电涡流传感器采集高速轴瞬时速度信息。每台机组采集信号时长为200 s,信号采集期间,机组均处于正常并网发电状态,并未因数据采集做出任何特殊控制处理。后续维修发现1号机组输入轴出现故障。
图2,3分别为2台机组的时域、2 000 Hz以内频谱图和时频分析。由于两台机组在200 s内转速波动大,因此,可以看出图2,3频谱图出现了频率混叠的情况,导致无法进行后续的信号处理与分析。

图2 1号机组时域、频域及时频分析结果Fig.2 Time domain,spectrum and the time-frequency analysis of the first wind turbine

图3 2号机组时域、频域及时频分析结果Fig.3 Time domain,spectrum and the time-frequency analysis of the second wind turbine
图4为1号机组振动信号通过IFDEO估计瞬时转速并进行阶次跟踪后的阶次谱图。
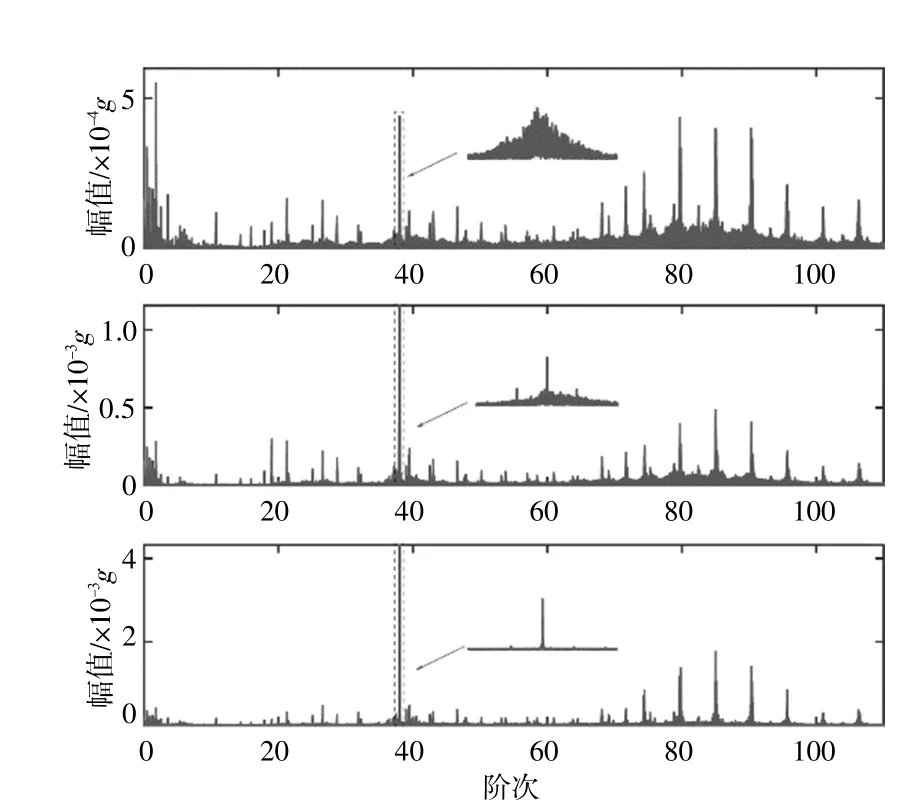
图4 1号机组IFDEO各次迭代阶次谱图Fig.4 Order spectrum of the first wind turbine in each iteration of the IFDEO
由于高速轴及其谐波振动振幅明显,因此以高速轴转速为参考阶次,依次提取高速轴0.5阶,19阶(高速轴齿轮啮合成分)以及38阶振动成分(2阶高速轴齿轮啮合成分)进行阶次跟踪。由于整段信号的振动成分复杂,转速波动剧烈(约为±13%),且多个振动成分阶次接近,因此在第一次进行提取0.5阶振动成分进行转速信息估计的过程中将整段信号等时间分成10段(每段有5 s的重叠以进行后续的拼接),每段信号的转速波动平均约为±3%。在此基础上,估计每段信号的0.5阶振动成分,最终通过汉宁窗将每段信号的瞬时频率拼接得到整段信号的瞬时频率估计。
随着迭代次数以及选取振动成分阶次的增加,阶次谱振动成分的模糊程度明显降低。随着瞬时频率精确度的提升,齿轮啮合频率的边频带与啮合频率分离。
图5为2号机组振动信号通过IFDEO进行瞬时转速估计并通过阶次跟踪得到的阶次谱图。

图5 2号机组IFDEO各次迭代阶次谱图Fig.5 Order spectrum of the second wind turbine in each iteration of the IFDEO
相较于2号机组,1号机组的阶次谱中出现了更多的频率成分。通过后续对2台机组的角度域振动信号提取包络得到各自的平方包络谱(图6,7)。由图6可知,其阶次成分为0.005 3以及其倍频,因此可推算出为风电传动系统输入轴松动(出现1/2X及其倍频)。

图6 1号机组阶次包络谱Fig.6 Order envelope spectrum of the first wind turbine
图8,9分别为第0.5阶振动成分进行窄带解调获取的瞬时转速进行阶次跟踪后的2台机组的阶次谱图。

图7 2号机组阶次包络谱Fig.7 Order envelope spectrum of the second wind turbine

图8 1号机组进行窄带解调阶次谱Fig.8 Order spectrum of the first wind turbine by using phase demodulation for IAS estimation
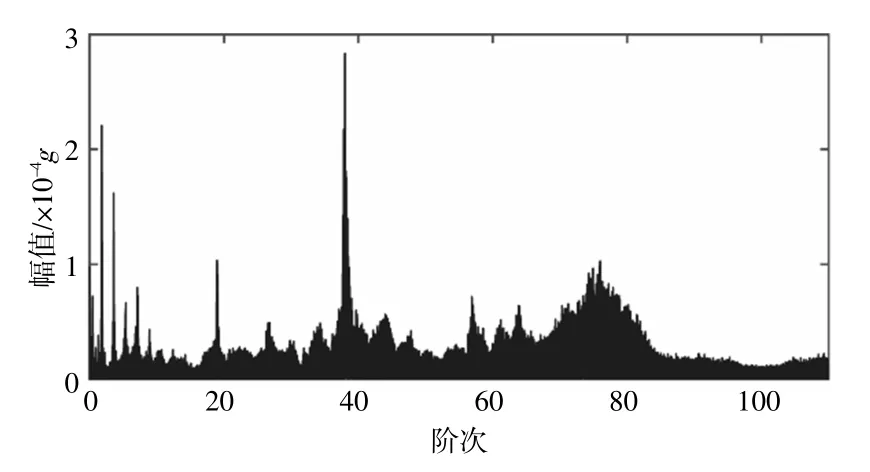
图9 2号机组进行窄带解调阶次谱Fig.9 Order spectrum of the second wind turbine by using phase demodulation for IAS estimation
由图8,9可知,由于振动信号的信噪比低和振动成分复杂的影响,相较于IFDEO的瞬时频率,估计出的瞬时频率误差更大,导致阶次谱中高阶振动成分频率与其边频带混淆,影响后续故障诊断结果。
图10,11分别为通过MOPA提取时频脊线后的2台机组的阶次谱图。图中选取了第1阶、2.5阶、18阶、36阶以及78阶时频脊线进行瞬时频率估计,虽然其准确度相较于提取单一的时频脊线有所提升,然而其仍具有信噪比低、时频分辨率低的特点,导致通过MOPA估计的瞬时频率误差较大,阶次谱图模糊,影响后续故障诊断的有效实行。
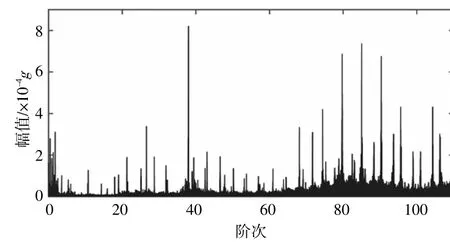
图10 1号机组MOPA阶次谱Fig.10 Order spectrum of the first wind turbine using MOPA for IAS estimation
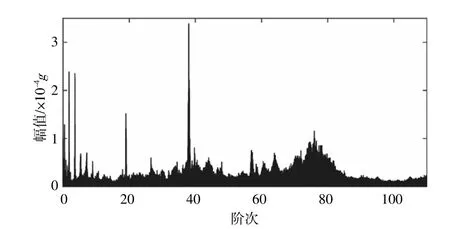
图11 2号机组MOPA阶次谱Fig.11 Order spectrum of the second wind turbine using MOPA for IAS estimation
图12,13分别为2台机组通过电涡流传感器采集的瞬时速度信号进行阶次跟踪的阶次谱。
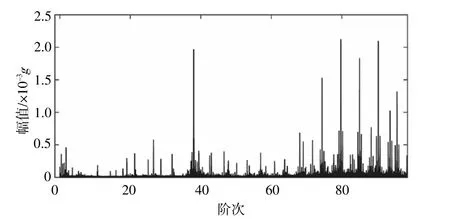
图12 1号机组通过编码器阶次谱Fig.12 Order spectrum of the first wind turbine using MOPA for IAS estimation

图13 2号机组通过编码器阶次谱Fig.13 Order spectrum of the second wind turbine using MOPA for IAS estimation
通过对比振动信号可以看出,本文提出的方法所得到的阶次谱(图4,5)能够将高阶振动频率分开(阶次谱频带60~100阶),并与图12,13的阶次谱最为相近。因此IFDEO能够保证后续解调获得的平方包络谱有效识别1号机组故障。
3 结论
本文提出了基于IFDEO的无键相瞬时频率估计方法,通过实际采集2台风电机组信号进行验证,确定该方法能够在变转速的情况下对风电机组传动系统输入轴松动进行有效识别。
①利用能量算子解调的方法提取瞬时频率的时频分辨率比通过提取时频脊线进行瞬时频率估计的时频分辨率高。
②与相位解调法相比,通过迭代提取更高阶的振动成分瞬时频率能够进一步提高瞬时频率的精确度,使得高阶振动成分在阶次谱中能够和临近振动成分有效分离。
③本文提出的方法能够更有效地提取感兴趣的振动成分的瞬时频率,并进行阶次跟踪。
④该方法不受硬件的限制,无需安置额外的传感器获取键相信号,因此能够降低风电机组的监测成本。
⑤该方法能够对长时间、大转速波动情况下采集的振动信号进行瞬时频率估计,因此能够作为需要长时间采集的信号(如时域同步平均法)的前期处理。
