纤维增强型软体驱动器的建模与分析

2022-11-23张梽轩潘剑飞徐东亮李英田

机床与液压 2022年20期

关键词：增强型端部软体

张梽轩，潘剑飞，徐东亮，李英田

(1.武汉理工大学机电工程学院，湖北武汉 430070；2.深圳大学机电与控制工程学院，广东深圳518060;3.中国科学院深圳先进技术研究院，生物医学与健康工程研究所，广东深圳 518055)

0 前言

软体机器人具有结构柔软性高、环境适应性好、人机交互性强、功能多样等优点[1]。近年来，随着柔性传感器[2]、3D打印技术[3]和智能材料[4]的发展，软体机器人以其良好的适应性和安全性已经成为机器人学的一个新方向[5-6]。

软体驱动器还可分为气体驱动器[7]、电驱动器[8]、腱驱动器[9]和粒子驱动器[10]。气驱软体驱动器可分为普通软体驱动器和纤维增强型软体驱动器[11]。

在气驱软体驱动器的研究中，纤维增强型软体驱动器显示了其强大的环境适应性，甚至能够在深海环境下进行无损取样[12]。同时国内学者也针对纤维增强型软体驱动器开发出了柔性夹持器，并对其进行相关的性能测试，包括夹持物体直径和对物体形状的适应性[13]。

与传统刚性机器人的控制不同，软体机器人的运动不局限于平面运动，这给软体机器人的控制带来了困难。由于它是由柔性材料制成的，其变形具有很强的非线性，很难获得分析运动数据并且很难建立精确的数学模型[14]。

此外，纤维增强型软体驱动器结构简单，可以提供较大的接触力，但纤维增强柔性弯曲执行器目前研究主要是基于实验，而对其变形和端部接触力的理论分析和建模很少。本文作者基于所设计的纤维增强型软体驱动器，分析纤维增强结构对驱动器弯曲变形的影响;建立驱动气压与驱动器弯曲角度的非线性数学模型和驱动器端部接触力的理论模型,通过有限元仿真和实验验证纤维增强型软体驱动器模型的有效性。

1 纤维增强型软体驱动器的设计

1.1 软体驱动器结构设计

为提高驱动器的负载能力，提出一种纤维增强型软体驱动器，由主体、不可拉伸层、纤维、外层共4个部分组成。驱动器的原型如图1所示。当气腔内气压大于大气压时，内部腔室膨胀，但是径向膨胀受到纤维的限制，底层膨胀受到不可延伸层的限制，所以夹持器可以向底部弯曲。

1.2 软体驱动器结构参数

与其他结构相比，纤维增强结构可以有效地限制腔室的径向膨胀。在高压下，驱动器的主要形变是弯曲，这使得端部接触力更大。文中主要研究纤维匝数和节距对驱动器性能的影响。驱动器的参数如表1所示。

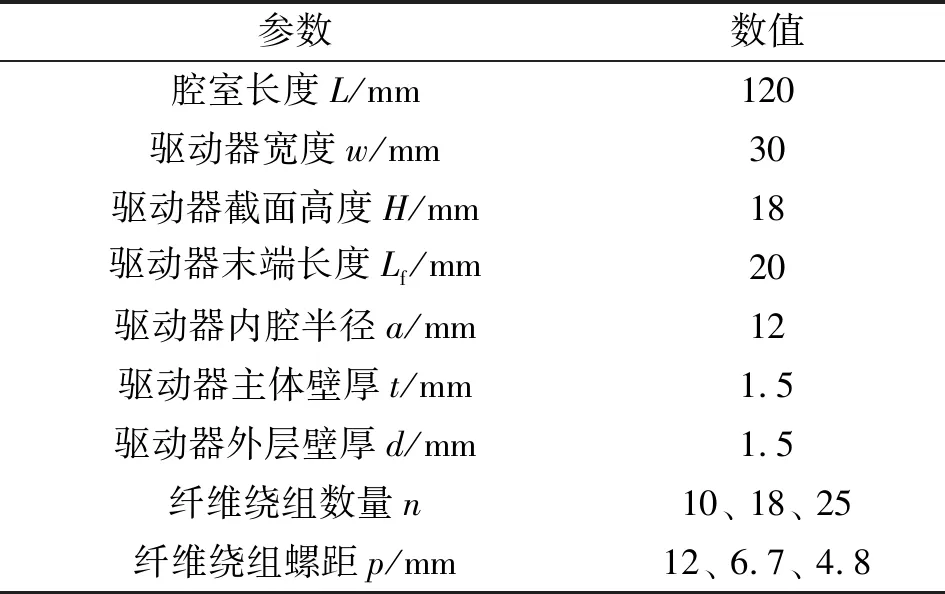
表1 软体驱动器结构参数

2 驱动器理论建模

2.1 纤维增强结构对软体驱动器的影响

首先，系统分析了纤维增强结构对驱动器的影响。文中的纤维增强结构采用双向交叉缠绕，具有潜在的扭曲效应[15]。纤维的排列完全由螺距决定。驱动器弯曲角度分析如图2所示。

螺旋角φ决定了在某一长度上致动器中纤维的匝数n。半圆柱弹性体的直径：

u0=2(a+t)

(1)

驱动器片段长度v0：

(2)

在变形过程中，v0是不变的，但是驱动器顶部的长度将超过原始长度v0，因为它不受限制层的约束。在此，假设纤维是不可延伸的，并且具有均匀的曲率。

因此，在没有压力之前，纤维长度l0、曲率半径Rl0、弧角2ψl0和纤维螺旋角φ的关系下:

(3)

(4)

l0=2ψl0Rl0

(5)

(6)

加压时，由于底部弯曲，上述参数发生变化。假设驱动器片段只能纵向弯曲，忽略横向弯曲和鼓包。半圆柱的高度是弯曲角度的函数。由于应变限制层的非延伸性和纤维增强结构，底部长度v0、直径u0和纤维长度l0保持不变。

驱动器片段的弯曲角度ψv可以表示为

(7)

参数Rl、n、ψl、v可以表示为以下函数：

l0=2ψlRl=2ψl0Rl0

v0=Rvψv

(8)

其中：Rv为驱动器加压时底面的曲率半径；h′为驱动器底面变形的高度。对于纤维增强结构截面：

h=Rl(1-cosψl)

(9)

(10)

由公式 (11)可知ψl是θ和n的函数ψl(θ，n) ：

(11)

2.2 纤维增强型软体驱动器建模

为进一步研究纤维增强型软体驱动器的运动特性和末端接触力，建立驱动器变形和末端接触力的理论模型是很有必要的。

根据文献[16]中硅胶材料的硬度分类，选择硬度为10A的硅胶作为软抓手的本体材料。采用Neo-Hookean超弹性模型描述硅胶材料的本构关系。建立主要的柯西应变方程[17]为

(12)

式中：G为弹性体的初始剪切模量；λi为轴向、周向和径向的主要拉伸比[18]。

(13)

根据方程(9)和(10)，以及硅胶材料的不可压缩性，轴向应力σ1可以表达为

σ1=G(1.5λ2-0.5/λ2-1)

(14)

对于柔软的手指，当一定的压力注入空腔时，在非限制层的点O附近产生3个弯矩，如图3所示。Ma为由点O周围的内部压缩空气产生的压力产生的弯矩；Mθ为材料拉伸产生的弯矩；Mf为执行器末端与外界相互作用产生的力矩。当Ma绕点O顺时针旋转时，Mθ和Mf绕点O逆时针旋转，满足扭矩平衡条件：

Ma=Mθ+Mf=Mt+Mb+Mf

(15)

图3中：patm为标准大气压；p1为注入的压力；a为腔室半圆截面的半径；b为底部厚度；t为驱动器壁厚；L为驱动器腔室长度；Lf为驱动器末端长度。

其中，hΦ可以表达为

hΦ=(a+τ)sinΦ+b

(16)

驱动器内外气压差pin可表示为

pin=p1-patm

(17)

弯矩Ma和内部输入空气压力之间的关系：

气压产生的弯矩Ma：

(18)

底部矩形部分的弯矩Mb为

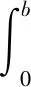
(19)

轴向应力σb和轴向拉伸比λb分别为

(20)

顶部半圆截面的弯矩Mt可以分解为Mt1和Mt2：

(21)

当驱动器与物体未接触时，驱动器的弯曲角度和空气压力之间的关系：

(22)

其中弯曲力矩Mθ是由G、a、b、t和θ构成函数,由于这个函数不能解析求解，所以不能得到函数的精确表达式，只能用数值计算。

此外，在点O附近达到扭矩平衡:

Mf=FLf=Ma=κpin

(23)

末端接触力F：

(24)

3 纤维增强型软体驱动器的分析

为验证柔性弯曲执行器变形理论模型的正确性，利用有限元分析软件ABAQUS建立仿真分析模型，对其运动特性进行仿真研究。

建模基于执行器制造过程，即对内层、外层、圆周纤维和不可延伸层进行建模并装配。其中硅胶主体部分采用美国Smooth-On公司的Dragon-Skin 10硅胶，Yeoh模型下材料参数C10=0.036 MPa、C20=2.58×10-3MPa、C30=-5.6×10-7MPa；不可延伸层的弹性模量设定为7.9 MPa，材料性质设定为无张力；纤维的弹性模量设定为31 076 MPa，泊松比为0.36。

在有限元分析的预处理阶段，对零件进行装配。纤维通过绑定约束包裹在主体和不可延伸层之外。部分结果如图4所示。

当施加不可延伸层与纤维增强结构时，驱动器的变形均匀，整个软体驱动器朝向限制的一侧进行弯曲变形，与后续的实际实验结果相符合。