五相直线电机混合空间矢量脉宽调制控制策略

丁强，石滕瑞，鲍旭聪

(1.南京工业职业技术大学电气工程学院，江苏南京 210023；2.江苏省风力发电工程技术中心，江苏南京 210023；3.南京航空航天大学自动化学院，江苏南京 210016)

0 前言

近几年，随着自动控制技术和微型计算机的高速发展，对各类自动控制系统的进给速度、加速度、快速定位精度等提出了更高的要求[1]。传统旋转电机加一套变换机构组成的直线运动驱动装置已不再能满足需求，而能够实现直接直线传动的直线电机，因省去中间转换装置，转换效率高，是当前的研究热点[2-3]。直线电机因起动推力大、动态响应快、定位精度高以及不存在传统旋转电机离心力的约束等优点[4-5]，在交通运输、数控机床、能源发电等领域已有广泛应用。

由于永磁体励磁不需要额外的绕组，可大幅度减小体积、节省成本[6]，永磁直线电机是当前应用最为广泛的直线电机类型。永磁直线电机是一个多变量、非线性、强耦合性的复杂系统[7-8]，故高效高精度的控制策略是实现直线电机高性能驱动的前提。当前直线电机的控制方式主要有：恒压频比(V/f)控制[9]、直接推力控制[10]以及矢量控制[11-13]等。前两者因控制精度不高、推力波动大，难以应用于高性能场合；矢量控制因较好的动态性能以及较高的控制精度，是当前直线电机最常用的控制方式。文献[14]为实现基于矢量控制的直线电机系统高精度抗干扰在线多参数辨识，提出一种新型自适应互联扩展卡尔曼观测器，提高了系统的鲁棒性。文献[15]基于直线电机矢量控制系统，提出一种定位力补偿二阶自抗扰控制器，提升了直线电机位置控制的抗扰性能及跟踪性能。文献[16]针对直线电机伺服系统易受不确定因素干扰影响位置跟踪精度问题，提出一种基于周期性扰动学习的自适应滑模控制方案，显著提升系统的动态响应性能和鲁棒性能，可以达到更高的位置精度。

为进一步提高推力密度，多相直线电机是今后的发展趋势[17]。五相直线电机因高推力密度、强容错能力以及较低的成本，是当前的研究热点[18]。但与此同时，多相化带来的拓扑结构复杂、系统谐波含量高以及控制算法复杂等问题，也对直线电机驱动系统提出了更高的要求[19-20]。

针对当前传统五相直线电机单空间矢量脉宽调制控制策略运行性能差、系统谐波含量高的问题，本文作者首先搭建了五相直线电机离散域解耦控制数学模型，为后续控制算法优化设计提供了基础。其次，为抑制系统谐波，文中提出了一种五相直线电机双混合空间矢量脉宽调制控制策略。为提高电压利用率，所提策略在采用两大电压矢量的基础上，引入额外2种电压矢量，通过合理分配电压矢量作用时间，达到抑制系统谐波的效果，提升电机运行性能。仿真与实验均充分验证了文中所提五相直线电机双混合空间矢量脉宽调制控制策略的有效性及优越性。

1 五相直线电机数字控制系统

为实现五相直线电机高性能运行，常采用空间矢量解耦控制策略，故五相直线电机离散化建模是搭建其数字控制系统的基础。

1.1 五相直线电机连续域解耦控制数学模型

由于直线电机具有复杂多变的电感和磁链，具有强耦合关系，因此为方便研究，在搭建五相直线电机数学模型时作出了如下假设：

(1)不考虑铁芯饱和、涡流、磁滞效应以及温度变化对电机参数的影响；

(2)电机气隙分布均匀；

(3)电机线圈绕组均匀分布在齿槽上。

由于五相直线电机多工作于电动机状态，所以文中以电动机的标注惯例对数学模型中的各个参数进行标注，其中相电流的参考方向与相电压的参考方向一致，与反电动势的参考方向相反。静止坐标系下的五相直线电机连续域数学模型主要包括：电压方程、电磁推力方程以及机械运动方程，如式(1)—式(3)所示。

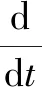
(1)

(2)

(3)

其中：U、I、e分别为相电压、电流、反电动势矩阵；R、L分别为相电阻、电感矩阵；v为电机运行速度；m为直线电机动子和负载的总质量；B为黏滞摩擦系数；Fm、FL分别为电磁推力、负载阻力。

为实现五相直线电机励磁、推力解耦控制，需要搭建五相直线电机dq旋转坐标系下数学模型。当前永磁电机的磁场定向控制策略常采用“id=0”的控制方案，基于此，五相直线电机dq旋转坐标系下数学模型如式(4)和式(5)所示。

(4)

(5)

其中：ud、uq、id、iq分别为dq轴定子相电压、电流；Rs为相等效电阻；Ld、Lq、ψd、ψq分别为dq轴相电感、磁链；ke为电机反电动势系数；Δθ为反电动势与电流的相位差。

1.2 五相直线电机离散化解耦控制数学模型

将式(3)—式(5)进行前向欧拉差分，可得到五相直线电机离散化解耦控制数学模型，如式(6)—式(8)所示。

(6)

(7)

(8)

其中：x(k)表示对应物理量k时刻的值；Ts为数字系统控制周期。

2 五相直线电机空间矢量脉宽调制策略优化设计

给出五相直线电机单矢量空间脉宽调制策略详细推导过程，并在此基础上，提出一种五相直线电机优化混合双矢量空间脉宽调制策略，降低系统谐波含量，提高系统整体效率。

2.1 基准电压空间矢量

五相逆变器一共有32种开关状态，即存在32个电压空间矢量，其基准电压空间矢量分布如图1所示。

由图1可知，五相逆变器的32个基准电压空间矢量将空间分成了均为36°的10个扇区，且其中30个非零矢量按照幅值大小可分为小矢量VS、中矢量VM和大矢量VL三大类，且大矢量的幅值为中矢量的1.618倍；中矢量的幅值为小矢量的1.618倍。

2.2 单空间矢量脉宽调制策略

为提高电压利用率，单空间矢量脉宽调制策略一般采用2个大矢量合成参考电压空间矢量，如图2所示。

当参考电压空间矢量所处扇区的扇区号为N时，假设该扇区顺时针、逆时针方向基准电压空间矢量(大矢量)作用时间分别为Ts1、Ts2。

图2结合伏秒平衡原则，可得：

(9)

(10)

其中：θe为电机电角度。

将式(9)、式(10)联立可计算得到：

(11)

即可得到基准电压空间矢量的作用时间。

2.3 双混合空间矢量脉宽调制策略

五相电机常采用星形连接形式，由于连接形式的限制，与传统三相星形连接不同的是，五相电机的谐波含量会比较丰富，主要为三次谐波，故需要在考虑三次谐波的基础上，对空间矢量脉宽调制策略进行优化设计。

五相逆变器三次谐波坐标系下的基准电压空间矢量如图3所示。

统一开关状态下，由图1及图3可知：

(1)在基波坐标系下对应的基准电压空间矢量幅值为大矢量而在三次谐波坐标系下为小矢量；

(2)在基波坐标系下对应的基准电压空间矢量幅值为中矢量在三次谐波坐标系下仍为中矢量。

故可利用上述基准电压空间矢量双坐标系下的对应关系，在单空间矢量脉宽调制的基础上，引入额外基准电压空间矢量，合理分配矢量，可达到抑制谐波的效果。

为提高电压利用率，文中采用双混合空间矢量脉宽调制方案，引入额外的中矢量，如图4所示，合理分配大矢量与中矢量的作用时间，以达到抑制五相直线电机三次谐波的效果。当参考电压空间矢量所处扇区的扇区号为N时，假设该扇区顺时针方向基准电压空间矢量大矢量、中矢量的作用时间分别为Td1、Td2；逆时针方向基准电压空间矢量大矢量、中矢量的作用时间分别为Td3、Td4。

由图4结合伏秒平衡原则，可得：

(12)

(13)

以第一扇区为例，在基波坐标系下的大、中矢量到三次谐波坐标系下成为小、中矢量，其对应关系如图5所示。

由图5可知，当基波坐标系下大矢量和中矢量的作用时间满足以下关系时：

(14)

4个基准电压矢量在三次谐波坐标系中合成电压空间矢量为0，即可达到抑制三次谐波的效果。

将式(12)—式(14)联立可得：

(15)

2.4 基于空间矢量脉宽调制策略的五相直线电机控制系统

文中采用五相直线电机控制结构框图如图6所示，是一个基于空间矢量脉宽调制控制策略的速度、电流双闭环控制系统。其中，空间矢量脉宽调制策略可采用传统单空间矢量脉宽调制策略方案，或文中所提双混合空间矢量脉宽调制策略方案。

3 仿真与实验

3.1 MATLAB/Simulink仿真结果及分析

对图6所示的五相直线电机双闭环解耦控制系统进行不同空间矢量脉宽调制策略方案的仿真验证，五相直线电机参数如表1所示。

表1 电机参数

MATLAB/Simulink仿真参数如表2所示。

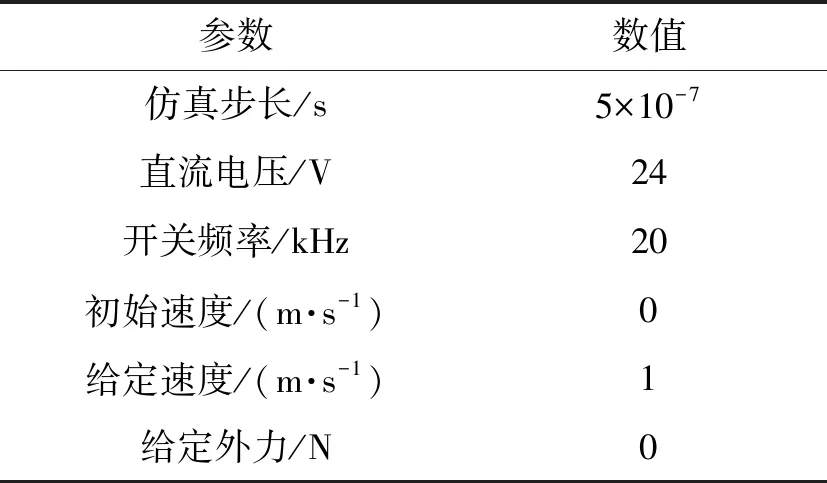
表2 仿真参数

对单矢量SVPWM算法与混合矢量SVPWM算法分别进行仿真，开关频率皆设置为20 kHz，五相直线电机相电流波形如图7所示，各相电流相位互差2π/5。

取五相中A相相电流如图8所示。可知:单矢量下相电流为削顶正弦波，即谐波含量较高；而混合矢量下相电流正弦度较好。相电流幅值前者在0.95 A左右，后者在1.05 A左右，电流频率二者相同，皆为125 Hz，与理论情况相符。

对2种算法下直线电机相电流分别进行快速傅氏变换(Fast Fourier Transform，FFT)分析，结果如表3所示。可知:单矢量SVPWM控制下的相电流总谐波失真(Total Harmonic Distortion，THD)数值约是混合矢量下的15倍;而单矢量SVPWM控制下的相电流谐波含量中绝大部分为三次谐波，相对基波分量的含量为19%。

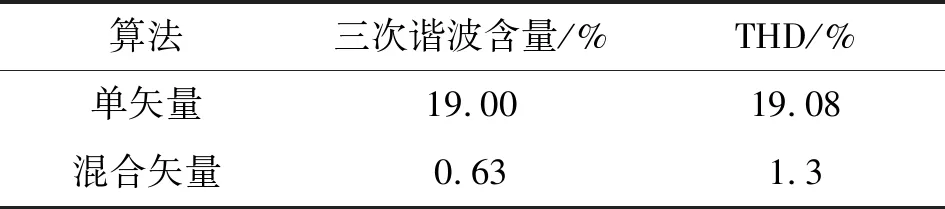
表3 相电流谐波分析数据

2种SVPWM算法控制下直轴电流id波形如图9所示，id最终稳定在0附近，与理论情况相符。单矢量下，id峰值约为0.087 A，在0.006 s左右进入稳态，稳态时有幅值约为0.006 A的脉动; 混合矢量下，id峰值约为0.29 A，在0.019 s左右进入稳态，稳态时有幅值约为0.007 A的脉动。相较而言，单矢量下的id波形稍好一些。

同样，作出交轴电流iq波形如图10所示，iq最终都稳定在恒值1.05 A附近，此值大小与外加推力FL有关，符合理论情况。单矢量下，iq峰值约为1.667 A，在0.031 s左右进入稳态，稳态时有幅值约为0.007 A的脉动; 混合矢量下，iq峰值约为1.2 A，在0.013 s左右进入稳态，稳态时有幅值约为0.007 A的脉动。相较而言，混合矢量下的iq波形较好一些。

在空载运行条件下，2种算法电磁推力波形如图11所示，Fm最终稳定在恒值0.03 N附近，因为电机本身存在一定阻力，故稳态时电磁推力会略大于外加负载力，不为零。单矢量下，Fm峰值约为0.048 N，在0.004 5 s左右进入稳态，稳态时有幅值约为0.000 6 N的脉动; 混合矢量下，Fm峰值约为0.034 5 N，在0.008 s左右进入稳态，稳态时有幅值约为0.000 43 N的脉动。可见，混合矢量下的电磁推力快速性稍差一些，但脉动比单矢量下的小一些。

电机运行速度v在不同SVPWM算法下的波形如图12所示，经过一段时间后，v最终都稳定在1 m/s，即给定转速，符合理论情况。单矢量下，v峰值约为1.04 m/s，在0.003 s左右进入稳态，稳态时有幅值约为0.000 52 m/s的波动; 混合矢量下，v峰值约为1.016 6 m/s，在0.007 s左右进入稳态，稳态时有幅值约为0.000 35 m/s的波动。可见，混合矢量下的运行速度稳态波动比单矢量下的更小。

对上述2种SVPWM算法从电流纹波、谐波含量角度分析总结可得：单矢量SVPWM算法控制下电流谐波含量很高，主要为三次谐波；混合矢量SVPWM算法不仅电流纹波小，且谐波含量低，对三次谐波有明显的抑制效果，控制效果更佳。

3.2 硬件实验结果及分析

文中采用基于DSP的五相直线电机驱动器，五相直线电机如图13所示，电机实验参数与仿真参数一致。

五相直线电机驱动器总体结构框架如图14所示。驱动器控制芯片采用TI公司的TMS320F2812，主要负责五相直线电机的数字控制与算法实现。

分别用单矢量SVPWM算法和混合矢量SVPWM算法驱动五相直线电机。设置电机空载运行，运行速度为1 m/s，此种工况下直线电机相电流波形如图15所示。可知：电流频率二者相同，约为125 Hz，单矢量下电流波形畸变严重，电流峰值达到2 A左右；而混合矢量下电流波形正弦度较好，电流幅值约为1 A，与理论及仿真结果一致。

2种算法控制下相电流FFT分析如图16所示。可得：单矢量SVPWM控制下的相电流THD数值较大，而混合矢量控制下则比较小，前者约是后者的5.5倍；单矢量SVPWM控制下的相电流谐波含量中绝大部分为三次谐波，约占谐波总量的86.7%，而混合矢量SVPWM算法下相电流三次谐波含量较小；其他次谐波含量2种算法控制下都差不多。说明五相直线电机中三次谐波问题严重，而混合矢量SVPWM算法抑制三次谐波具有较好效果。

4 结论

针对五相直线电机传统单空间矢量脉宽调制控制策略运行性能差、系统谐波含量高的问题，文中提出一种双混合空间矢量脉宽调制策略。为提高电压利用率，所提方案引入额外的中矢量，通过合理分配大矢量与中矢量的作用时间，以达到抑制五相直线电机三次谐波的效果。仿真与实验结果表明：与传统单空间矢量脉宽调制策略相比，使用文中所提双混合空间矢量脉宽调制策略方案的五相直线电机系统谐波含量明显降低，提高了系统效率，且电机运行性能得到显著提升。