一种用于超声螺栓预紧力测量的时延算法

冉毅川，毛延翩，姬升阳，陈 兵，张承俊，刘德新

(1.中国长江电力股份有限公司，宜昌 443000;2.西南交通大学 材料科学与工程学院，成都 610031)

螺栓是工程生产中重要的连接方式之一，具有结构简单、使用方便、效率高、成本低等优点，被广泛应用于核动力工程、水利水电、交通桥梁、建筑结构、化工产品等领域中。传统的螺栓预紧力测量方法有扭矩扳手法、电阻应变片法等，但大多由于存在控制精度差、测量效率低等问题，在螺栓预紧力监测方面的应用还存在一定的局限性。历经多年研究，基于声弹性原理的超声波测量法的理论日趋完善。其中，超声纵波法因其沿中轴传输，对柱状形状的螺栓具有极高的灵敏度，被广泛应用于螺栓预紧力的工程测量[1-3]。

核动力工程、水利水电、航天航空等重大工程领域中，需要快速对螺栓预紧力进行监测，这要求超声螺栓预紧力估计算法具备较快的运算速度。现有超声螺栓预紧力测量方案采用的数据采集卡采样速率较低，若不采用插值算法，其预紧力分辨率不能满足工程测量的分辨率需求。为进一步降低预紧力分辨率，常采用时域插值算法。但对于超声回波信号而言，时域插值算法存在计算量比较大的问题，计算复杂，无法满足实时测量的要求[4]。

基于此，首先分析了超声螺栓预紧力测量原理，得到纵波法预紧力测量公式，并搭建了超声螺栓预紧力测量系统；其次分别对频域升采样原理、频域互相关时延估计算法进行了理论推导，并将二者相结合提出了一种用于超声预紧力测量的频域补零互相关时延估计算法(ZPCC)；最后通过仿真和测量进行验证，结果表明该方法能够精确快速地实现超声螺栓的预紧力测量，且效果明显优于传统算法效果。

1 超声螺栓预紧力测量方法

1.1 测量原理

该方法是基于声弹性理论和胡克定律,利用超声纵波渡越时间与螺栓预紧力的关系来测量螺栓预紧力的[5]。考虑在弹性范围内，对螺栓加载应力σ，由胡克定律可以得到

(1)

L0=L1+L2

(2)

式中：E为材料弹性模量；Lσ为螺栓在加载应力σ下的夹紧长度；L0为螺栓在零应力状态下的总长度；L1为螺栓在零应力状态下的夹紧长度；L2为螺栓不受力长度。

根据声弹性原理，超声波波速与超声传播区域应力呈以下关系[6]

σ=0(1+A·σ)

(3)

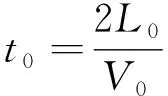
(4)

式中：σ为应力下超声波波速；0为零应力下波速；A为声弹性系数；t0为零应力下回波渡越时间。

联立式(1)～(4)，得到螺栓加载应力σ时纵波的渡越时间tσ为

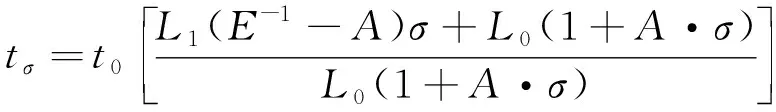
(5)

令Aσ≪1，式(5)可简化为

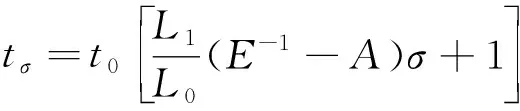
(6)

设应力系数为K，则有

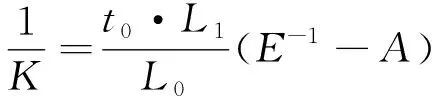
(7)

令F=σ，则螺栓应力测量公式可简化为

F=K(tσ-t0)

(8)

式中：F为螺栓预紧力(拉力为正，压力为负)；K为影响预紧力的系数。

式(8)表示弹性范围内螺栓预紧力与零应力状态和加载应力状态下的渡越时间差成线性关系，简化了超声波法对螺栓应力的测量。

1.2 测量系统

超声螺栓预紧力测量系统包括发射接收信号单元和数据采集单元。发射接收信号单元由多通道的超声发射接收板卡中的FPGA(现场可编程逻辑门阵列)控制模块控制，高压发射模块和回波处理模块完成信号的发射和接收。数据采集单元由一块采样率达1.25 GHz的数据采集卡构成，实现数据采集和模数转换功能。工控机协调控制发射接收信号单元和数据采集单元，并对超声信号进行处理，得到超声时延。超声螺栓预紧力测量系统框图如图1所示。

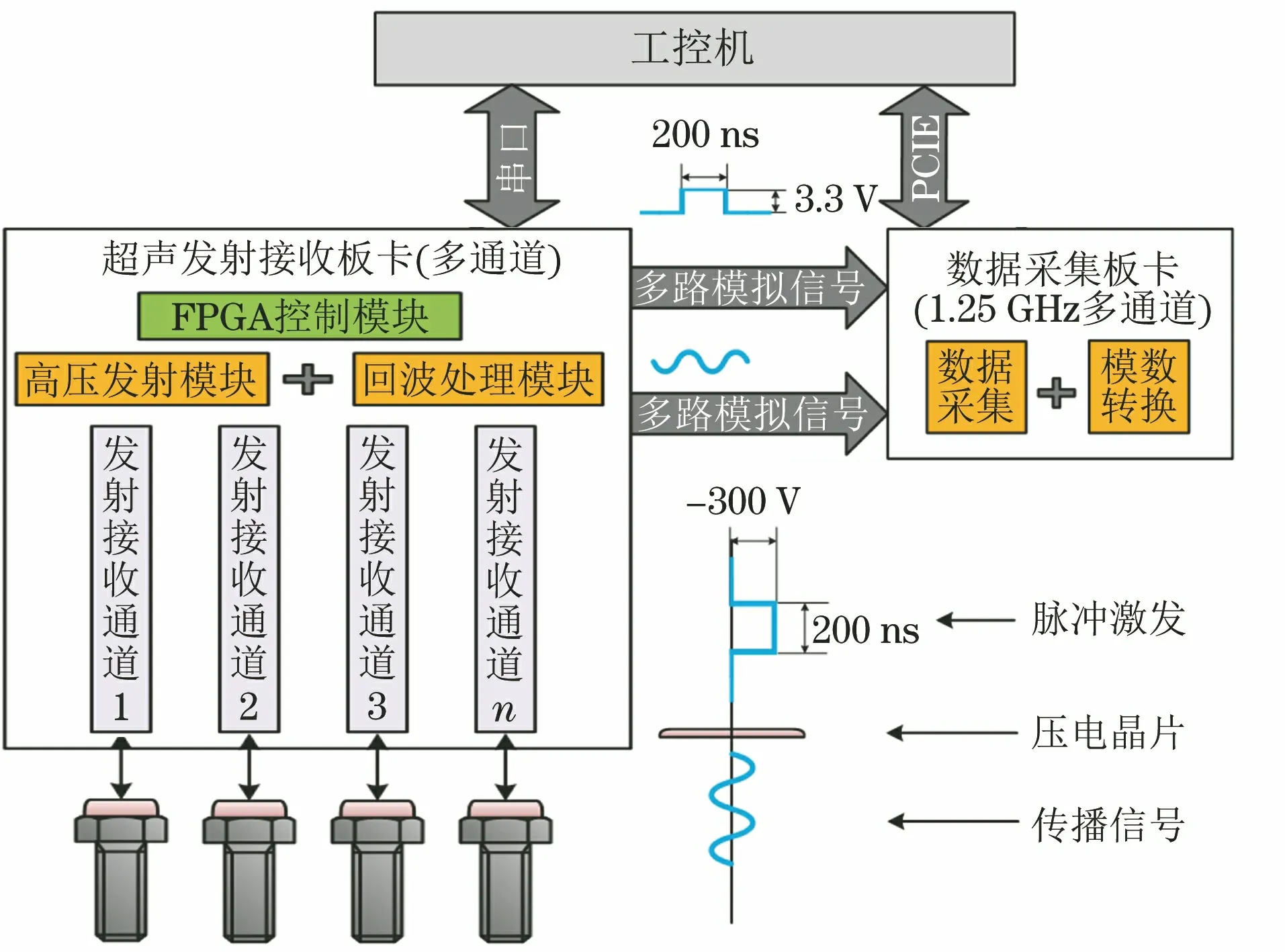
图1 超声螺栓预紧力测量系统框图

2 频域补零互相关时延估计算法

2.1 信号频域升采样原理

升采样是指利用算法对离散波形信号进行处理，从而达到提高数据采样率的目的。信号升采样的时域实现过程是在原序列s(n)相邻数据间插入L-1个0，然后通过低通滤波滤除多余的频谱分量，从而得到L倍升采样序列y(L·n)[7]。

信号进行时域插零等效于信号在频域进行频谱周期拓展，插零后进行低通滤波，等效于滤除延拓频谱[8]。这一过程和在原信号频谱Z(m)上进行补N个零的操作是等效的。因此，对信号进行L倍升采样的频域处理过程可表示为：① 对原信号s(n)进行傅里叶变换得到频谱Z(m);② 对频谱Z(m)进行补零操作，补零个数为(L-1)N，得到频域Y(l)；③ 对Y(l)进行逆傅里叶变换，即得到升采样信号y(k)。

2.2 互相关时延估计算法

互相关函数R(x,y)表示的是两个时间序列之间的相关程度，可以用于评判两个波形的相似度[9]。根据离散互相关运算的时域表达式和离散卷积运算的表达式可以看出，离散互相关就是原信号反褶后进行离散卷积，同时时域卷积等价于频域乘积、时域反褶等价于频域共轭。因此互相关函数的频域表达式为

R(x,y)=IDFT{DFT{x}*∘DFT{y}}

(9)

式中：DFT为离散傅里叶变换；IDFT为离散傅里叶反变换；∘为同维向量的对应项相乘；*为对复信号取共轭。

互相关函数R(x,y)峰值点位置可作为时延估计值[10]，因此频域互相关时延估计算法流程可表示为：① 对信号x，y进行傅里叶变换，得到频谱信号Zx和Zy；② 对Zx取共轭得到Zx*；③Zx*和Zy元素相乘，得到互相关函数的频谱ZR(x,y)；④ZR(x,y)进行逆傅里叶变换，得到互相关函数R(x,y)；⑤R(x,y)峰值点位置则为时延估计值。

频域升采样需要先进行傅里叶变换，再进行补零，最后进行逆傅里叶变换，而互相关时延估计也会先后对信号进行傅里叶变换和逆傅里叶变换，因此可以在互相关时延估计算法①后，对频谱信号Zx和Zy增加补零操作，达到减小离散互相关函数R(x,y)的时间间隔，提高时延估计分辨率的目的。这就是频域补零互相关时延估计算法的基本思想，频域补零互相关时延估计算法流程图如图2所示。

图2 频域补零互相关时延估计算法流程图

3 试验与分析

3.1 超声时延算法对比

为了验证互相关时延算法的正确性，笔者进行了寻峰算法(利用波峰值确定时延)和互相关算法的计算效果对比，对比试验有以下三个步骤。

(1) 选取一段噪声较少的超声信号作为原始信号，将原始信号延迟50个数据点得到延迟信号，原始信号波形如图3所示。

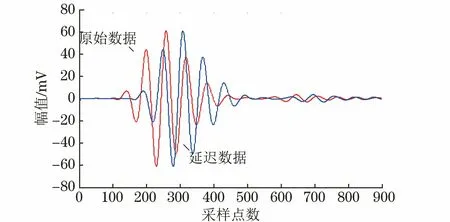
图3 原始信号波形

(2) 为模拟现场工况环境采集到的超声信号，在延迟信号中分别叠加60，30，20，15，10，5 dB的噪声信号，加噪延迟信号波形如图4所示。

(3) 分别采用寻峰算法和互相关算法计算原始信号和加噪延迟信号的时延，并和理论值50进行对比。

从图4可以看出，随着信噪比的降低，延迟信号质量越来越差。分别使用寻峰算法和互相关算法计算原始信号和加噪延迟信号的时延，并和理论值50对比，得到不同算法的时延估计如图5所示。

图4 加噪延迟信号波形

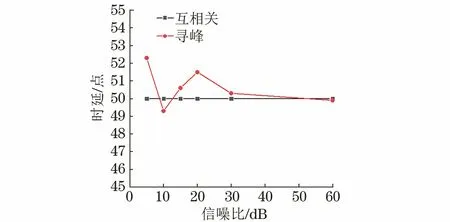
图5 不同算法的时延估计

从图6中可以看出，在高信噪比的条件下寻峰时延算法和互相关时延算法效果相当；但随着信噪比的减小，波形信号变差，寻峰时延算法计算结果变得不稳定，而互相关时延算法在低信噪比条件下，由于其本身还具有一定的降噪能力，所以计算结果稳定。因此文章后续采用的时延估计算法均为互相关时延估计。

图6 8.8级M30螺栓实物

3.2 不同插值算法测量效果对比

为验证频域补零互相关时延估计算法是否能精确快速地实现超声螺栓预紧力测量，文章选取水电领域常用的8.8级M30×150(长为150 mm)碳钢螺栓在拉伸机上进行加载试验，并利用不同插值互相关时延算法估算其超声时延，从算法速度和预紧力估计精度两个方面对算法进行评估。试验主要材料及设备规格如表1所示，8.8级M30螺栓实物如6所示，试验现场如图7所示。

图7 试验现场

表1 试验主要材料及设备规格

3.2.1 螺栓应力系数标定

标定试验分别测量螺栓在零应力状态和加载应力状态下的一次回波信号，利用互相关时延估计算法得到不同加载应力下的超声时延，通过线性拟合建立应力与时延的标定直线，直线斜率即为应力系数K，标定数据如表2所示，应力系数标定曲线如图8所示。

图8 应力系数标定曲线

从表2可以看出，针对该试验可选取螺栓应力系数K=1.680 MPa·ns-1；同时可以看出Pearson系数大于0.99，说明标定数据具有良好的线性关系。

表2 应力系数标定数据

3.2.2 螺栓预紧力测量

为验证ZPCC算法的有效性，在拉伸机上对螺栓以20 MPa为步长进行加载，待加载载荷稳定后采集超声回波信号，并选取相同长度波形(约10 000点)，使用MATLAB软件在dell 7910工作站上利用线性插值互相关算法(LCC)、三次插值互相关算法(PCC)、三样条插值互相关算法(SCC)和频域补零互相关算法插值16倍计算其时延Δt，结合式(8)，得到测量预紧力，并与加载值进行对比，利用式(10)计算相对误差值，不同插值时延估计算法测试结果如表3所示，不同算法误差曲线如图9所示。

(10)

式中：δ为相对误差；σtest为超声法测量得到的轴向应力；σref为拉伸机加载的轴向应力。

由图9可以看出，随着加载轴向应力的增大，测试误差在逐步减小，在80 MPa以后误差趋于平缓，因此将大于80 MPa的测试数据称为误差稳定区。

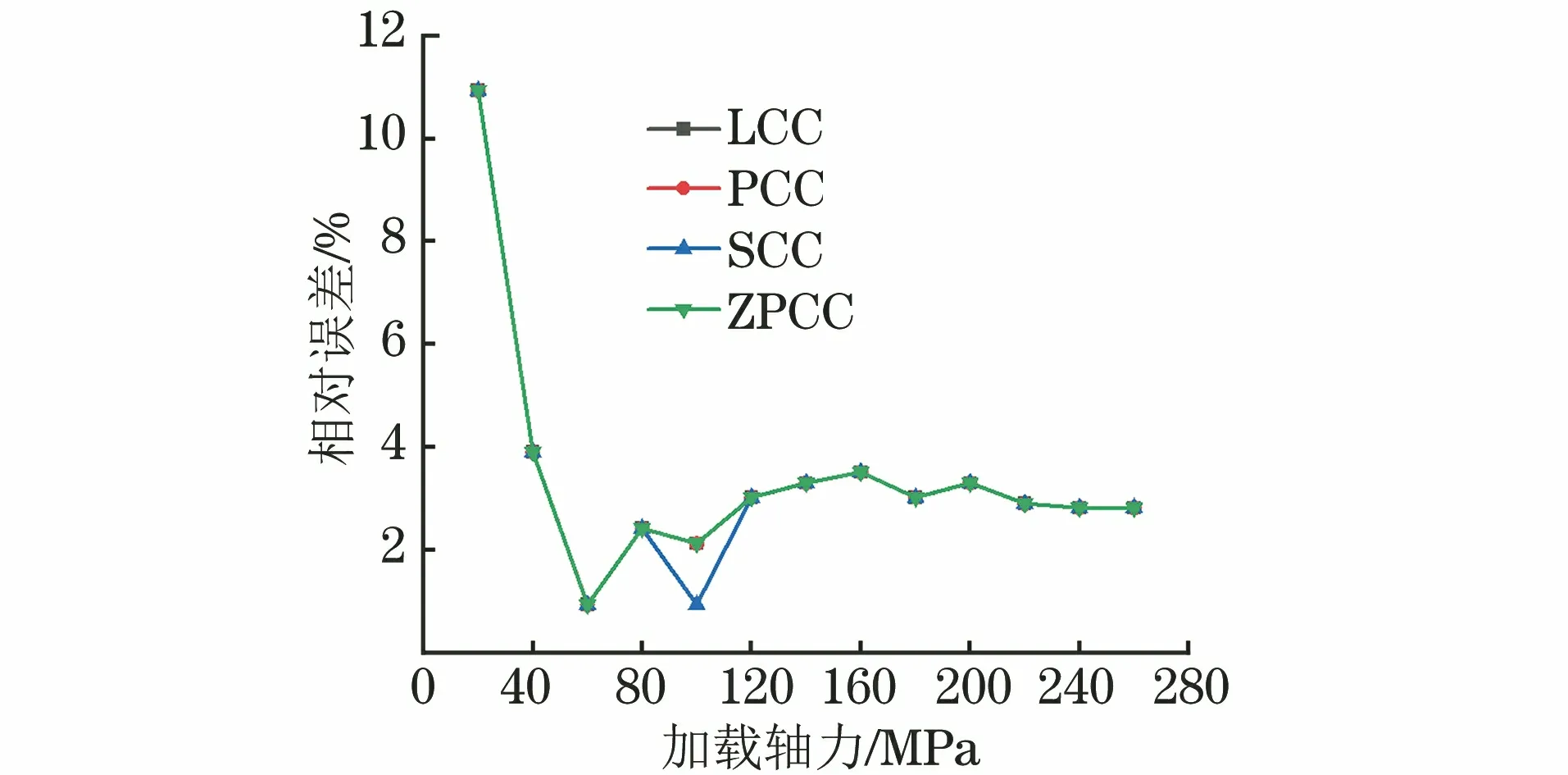
图9 不同算法误差曲线

由表3可以看出，不同插值时延估计算法的测量误差均小于3.5%，但运算速度有所差异，线性插值互相关算法、三次插值互相关算法和三样条插值互相关算法的单点运算速度均大于50 ms；而频域补零互相关算法运算速度仅为10.62 ms，提升了约5倍，这说明频域补零互相关算法在具备传统算法测试精度的同时，还拥有更快的运算速度。

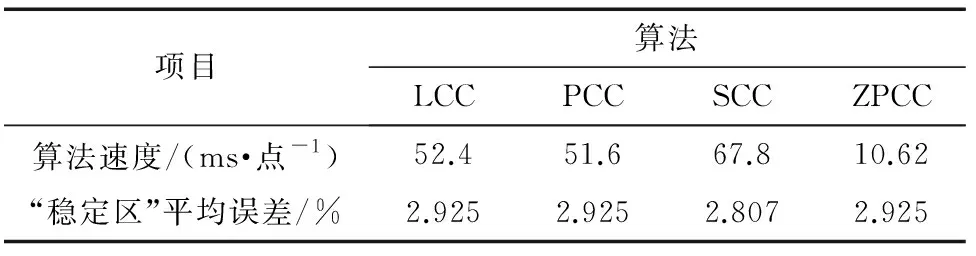
表3 不同插值时延估计算法测试结果

4 结语

根据声弹性原理和胡克定律推导了纵波法预紧力测量公式，搭建了超声螺栓预紧力测量系统，该系统最高硬件采样率可达1.25 GHz，硬件声时分辨率为0.8 ns；通过将频域升采样原理、频域互相关时延估计算法相结合，提出了一种用于超声预紧力测量的频域补零互相关时延估计算法；采用仿真的方式验证了互相关时延算法在低信噪比条件下，具有一定的降噪能力，且计算结果稳定。

选取8.8级M30×150碳钢螺栓进行标定试验，确定了该型号螺栓的应力系数为1.680 MPa·ns-1；对该型号螺栓的加载试验结果表明，频域补零互相关算法测试精度可达3.5%，与传统算法相当，但运算速度提升了500%。