忆阻电路系统事件触发脉冲稳定性研究
2022-11-22覃宇燕
曾 旺,覃宇燕,宓 茜
(1.湖南工业大学 理学院,湖南 株洲 412007;2.湖南工业大学 电气与信息工程学院,湖南 株洲 412007)
0 引言
1971年,美国加州大学华裔科学家蔡少棠教授首次提出了忆阻器[1](memristor)的概念,称其为除了电阻、电感和电容之外的第四种基本电路元件,并在文献[2]中阐述了元件的特性、原理及应用。直到2008年,惠普公司的研究人员首次宣布了忆阻器的固态实现[3]。忆阻器具有保留电路中通过电荷的能力与特性[4],在传统的电路设计、信号处理、自动化控制以及神经网络等领域拥有广泛的应用空间和发展潜力,因而受到了学术界的广泛关注[5-8]。
用忆阻电路中的忆阻器替代原来的二极管是实现忆阻电路系统设计、制造和控制的基本思路。由于涉及系统内多个不同部件的混沌控制,因此这个方法具有较高的挑战性。文献[9]研究了忆阻混沌系统的模糊建模和脉冲控制问题,将忆阻混沌系统建模为T-S 模糊系统,解决了其脉冲稳定性问题。基于文献[9]提出的T-S 模糊模型,文献[10]研究了在间歇控制下忆阻系统的指数稳定性问题。文献[11]研究了具有不确定性的忆阻蔡系统的事件触发滑模控制。
在具体的应用实践中,来自不同领域的专家学者对脉冲控制的实现做了大量尝试,并获得了丰富的成果[12-15],但事件触发机制问题是应用实践的一个技术难题。由于脉冲控制仅在必要时才执行,事件触发的持续监测和精确快速反应,一直是脉冲控制领域中的热点问题[16-19]。文献[16]利用分布式事件触发脉冲控制方法,研究了多智能体系统的领导-跟随者一致性问题。文献[17]在李雅普诺夫方法的框架下,利用事件触发脉冲控制方法,研究了非线性时滞系统的指数稳定性。文献[18]利用基于事件的脉冲控制方法,研究了连续时间动态系统的指数稳定问题及其在忆阻神经网路同步中的应用。文献[19]在基于脉冲微分的李雅普诺夫稳定性理论和有限时间控制方法下,利用分布式事件触发脉冲控制策略,研究了非线性多智能体系统的有限时间一致性问题。
受上述研究成果的启发,本文针对忆阻电路系统,提出了一种基于T-S 模糊模型的事件触发脉冲控制方法,并研究了其稳定性,以期为T-S 模糊模型事件触发脉冲控制的进一步研究,提供一种新思路。
1 预备知识和模型描述
本节主要介绍了相关的符号和预备知识。In表示n阶单位矩阵。对于矩阵A(或向量x),AT(或xT)表示A的转置(或x的转置)。Det(M)表示方阵M的行列式,Re(λ)表示复数λ的实部。
2008年,Itoh 和Chua 提出了基于忆阻器的忆阻混沌电路,如图1所示。
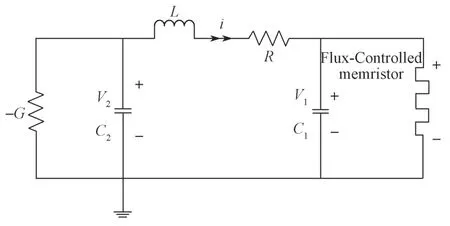
图1 基于忆阻器的混沌电路系统Fig.1 Memristor-based chaotic circuit system
首先,将Hewlett Packard(HP)忆阻器描述为以下形式:
v=M(q)i,或i=W(φ)v。
式中:v、i分别为电压和电流;
图1的电路系统可以描述为以下方程

式中u(t)为控制协议,将在后文详细介绍。
令x1(t)=V1(t)、x2(t)=V2(t)、x3(t)=i(t)、x4(t)=φ(t),以及,从而有

系统(2)可写成如下形式:


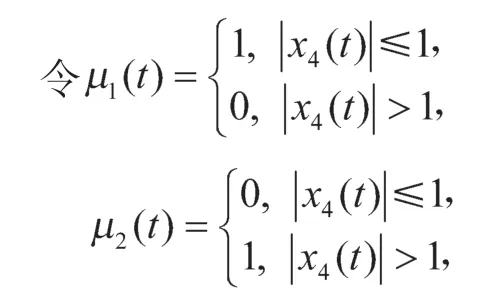
利用T-S 模糊模型,可得

2 主要结论
为了研究忆阻电路系统的稳定性问题,本节提出一种事件触发脉冲控制算法:

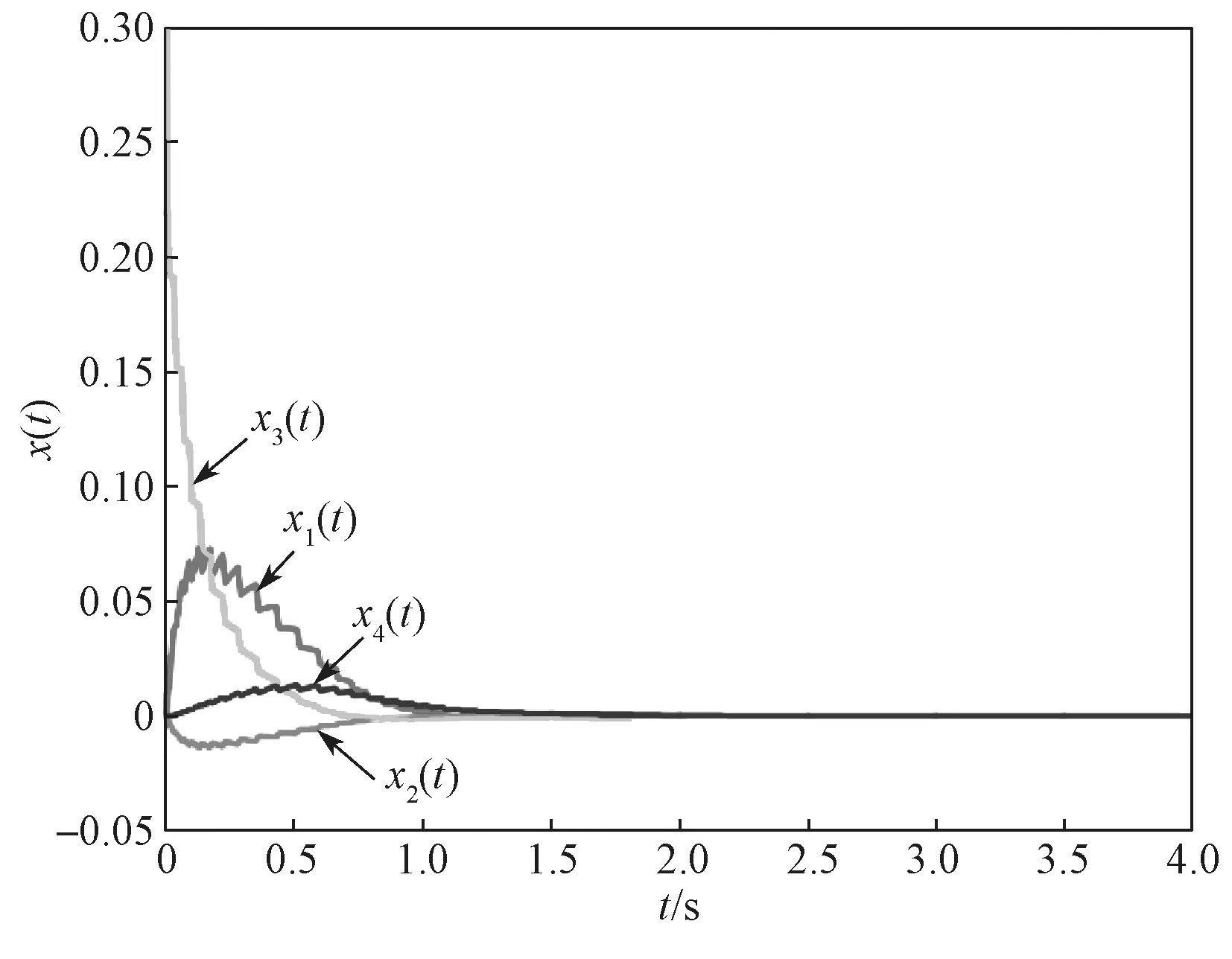
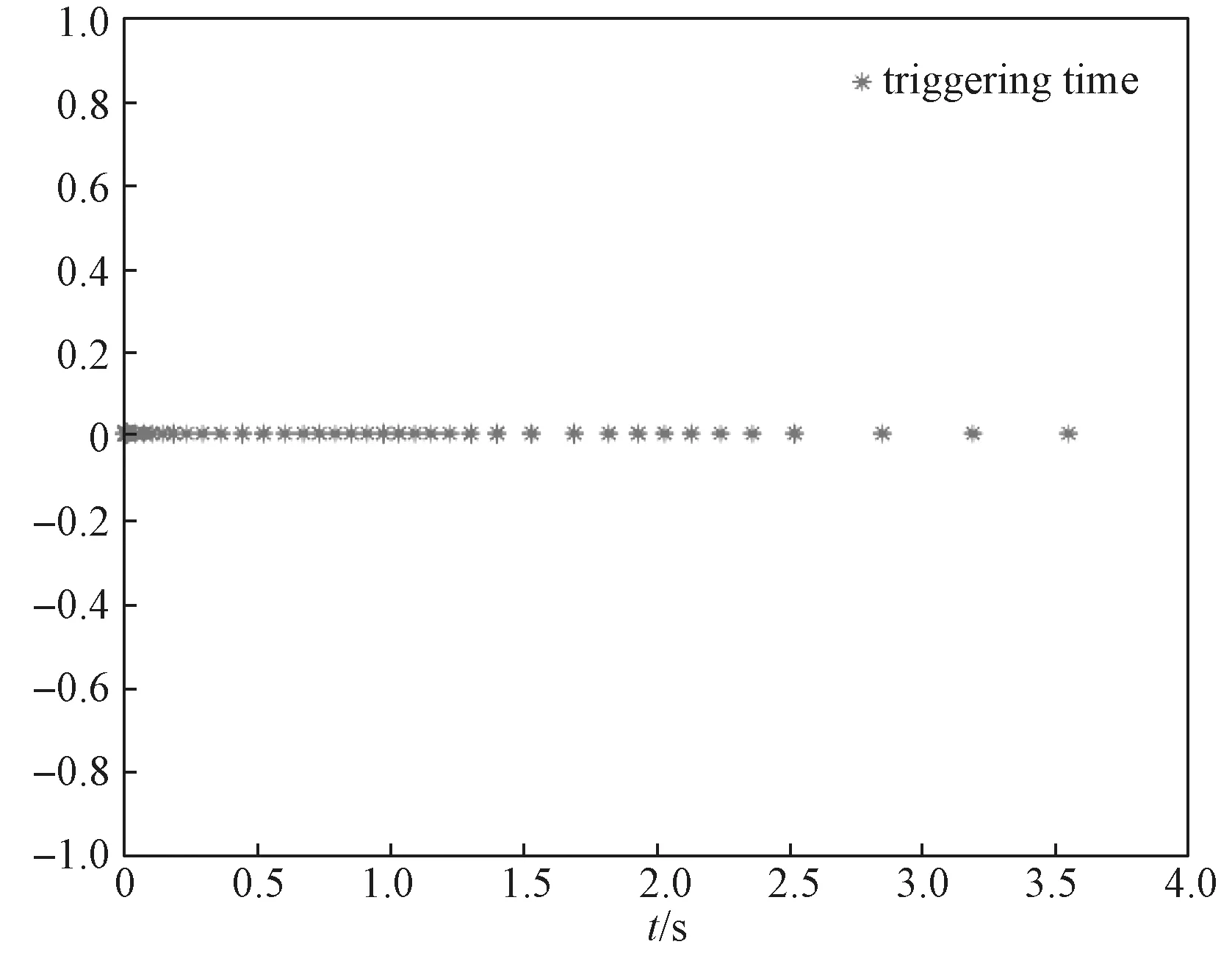
式中:λ为一个给定的增益,且-1<λ<0;δ为Dirac脉冲函数;tk(k=0,1,…)为智能体i的事件触发时间序列,且t0 在控制协议(5)下,系统(4)可写为 式中:事件触发时间序列tk定义为 其中事件触发函数f(t)定义为 定理1在事件触发条件(7)下,若控制协议(5)中控制增益λ满足-1<λ<0,则忆阻电路系统(4)可以达到渐进稳定,并排除了Zeno 行为的发生。 证明考虑如下李雅普诺夫函数 首先,证明忆阻电路系统(4)在控制协议(5)下可以达到稳定,即当时,如果 则有 一方面,注意到0<1+λ<σ<1,根据式(10)可知,如果 则有 从而得 根据式(7)和式(8)有 这时必然存在一个正常数β,满足σ2<β<1,从而有 因此,当t→∞时,k→∞,从而V(t)→0,也就是x(t)→0。 再证明忆阻电路系统Zeno 行为不存在,即两个触发时刻之间的间隔是正的。 从而有 根据式(4)和式(5)可得 从而有 这就证明了忆阻电路系统Zeno 行为不存在。 本节用数值仿真来说明控制协议(5)的有效性,且在所提控制协议下,忆阻电路系统(4)是可镇定的。 对于图1中的忆阻器电路系统,相关参数取值选择如下:C1=0.15,C2=0.8,R=0.1,G=1.5,L=1;同时选取a=0.3,b=0.1。显然,A1、A2可表示为 再选取控制增益λ=-0.2,事件触发函数(8)的参数σ=0.9。仿真结果如图2和图3所示。 图2 仿真所得x(t)的状态轨迹Fig.2 State track of simulated x(t) 图3 事件触发时间Fig.3 Event-triggered time 从图2中x(t)的状态轨迹可以看出,在控制协议(5)和事件触发条件(7)下,忆阻电路系统(4)是渐进稳定的。从图3中事件触发时间可以看出,系统排除了Zeno 行为的发生。 本文讨论了忆阻电路系统事件触发脉冲稳定性的问题。首先,利用T-S 模糊化方法进行建模,得到相应的线性系统模型。再结合事件触发控制理论、脉冲控制理论,提出了一种事件触发脉冲控制协议,再通过Lyapunov 稳定性理论,给出系统达到稳定的条件。最后,通过数值仿真,验证了所得结果的有效性。


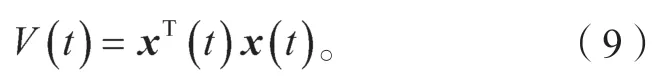
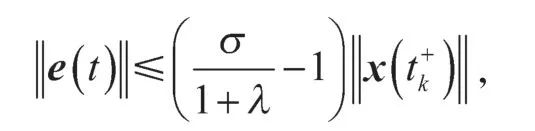










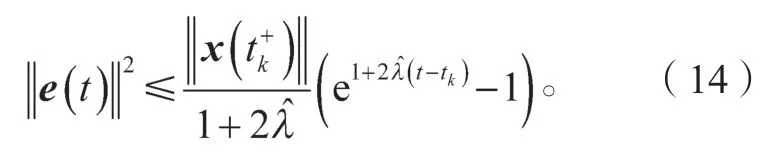


3 数值仿真

4 结语
