计及新能源消纳的县域电网侧储能削峰填谷优化策略研究

朱昊，王佳峰，周安仁，岑梁，牛传臣，黄琪萍，刘新斌

（1.国网浙江省电力有限公司长兴县供电公司，浙江 湖州 313100；2.浙江省长兴县住房和城乡建设局，浙江 湖州 313100）

在2030碳达峰、2060碳中和目标要求下，国家已经明确要建立以新能源为主体的新型电力系统，新能源装机的快速提升，以及电力系统正在发生的变化，使得储能刚需属性愈发增强。储能是解决新能源消纳问题的最佳方案。新能源装机的增长，加大了电网消纳压力，配置储能是主要解决方式，政策已明确配置比例要求和优先消纳[1-2]。近年来，在技术进步、需求增长、政策支持等多重因素共同影响下，我国电力储能技术应用快速发展且已初具规模。

在电网侧，为应对新能源大发展和特高压电网建设，须提高电网调节灵活性及稳定性。储能系统具有能量高、安装灵活、充/放电速度快等特点，可以在不改变现有电网结构的基础上平抑新能源功率波动、缓解常规机组调峰压力、提高新能源消纳水平，同时储能在电网侧的应用，能够缓解电网阻塞、延缓输配电设备扩容升级、辅助发电侧进行调峰，还能参与电力辅助市场服务，包括系统调频和备用容量[3]。

储能系统在配电网削峰填谷方面的优化已有广泛研究。文献[4]提出规模化分布式光伏并网条件下含储能电站的优化调度方案，兼顾系统经济性和风电优先调度的情况下，利用储能电站实现了削峰填谷。文献[5]提出一种基于移动式储能削峰填谷的双层优化调度模型，以改进增强烟花算法进行求解，最终实现可靠性与经济性的移动式储能最优调度策略。文献[6-7]采用改进鱼群算法、模拟退火等智能算法求解含储能装置的电力系统削峰填谷最优策略问题。但是，现有文献所提出的控制策略很难在考虑多种约束条件下实现储能对电网的削峰填谷优化，且在不同负荷场景下的应用缺乏对比，使得控制策略选择缺乏理论依据。

本文以存在新能源消纳问题的某县域东南部电网为例，开展计及新能源消纳的电网侧储能削峰填谷优化策略研究，利用储能系统双向功率特性和灵活调节能力，建立“新能源+储能”优化调度模型，在不同负荷场景下进行仿真，仿真结果表明该模型能够有效缓解新能源反调峰带来的压力，进一步提升县域电网风电、光伏等新能源的可控性和渗透率。

1 储能运行数据分析

储能可以日常参与电网调峰，满足地区“早高峰+晚高峰”电力供应需求，有效降低峰谷差，优化负荷特性；同时储能具备毫秒级响应调度指令能力，能够参与电网调频和调压；紧急状况下，能够提供快速功率支撑，提高电网暂态稳定性；纳入源网荷储统一管理，与精准切负荷系统配合，实现储能电站源荷快速转换，增加电网安全稳定裕度。

目前，某县供电公司储能电站在日常工作中执行“一充两放”运行策略，在特殊情况下，根据电网运行需求，适时调整其充放电策略，例如，在主网四线断面须有效控制期间、春节无功管控期间等。2021年7月储能电站日常充放电曲线，如图1所示。

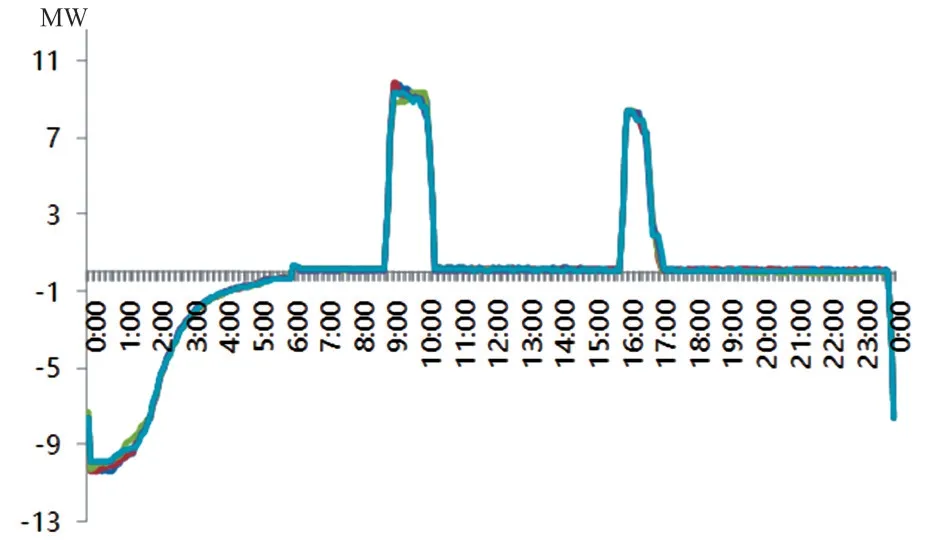
图1 2021年7月储能充放电曲线

针对储能充放电功率数据，统计自储能电站正式投运以来近10个月，在每日0:00—24:00时间段内进行储能电站充放电功率累加求和，进一步深度观测其充放电功率的时间段概率分布，如图2所示。

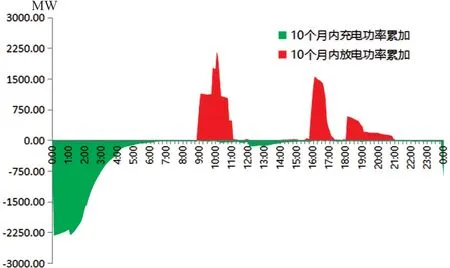
图2 储能充放电功率累加曲线

由图2可知，储能充电模式主要集中在每日的0:00—6:00；放电模式主要集中在每日的9:00—11:00、16:00—17:00以及18:00—21:00，其中以9:00—11:00、16:00—17:00两个放电模式时间区间出现概率较高。在目前储能充放电策略的基础上，本文考虑新能源消纳问题，进一步开展储能充放电优化策略研究。

2 “新能源+储能”调度模型构建

在考虑新能源消纳问题的情况下，通过储能充放电优化策略对某县域东南部电网统调负荷进行平抑优化调度，来进一步缓解常规机组的调峰压力。本文基于MATLAB仿真平台，根据县域东南部电网负荷特性，以及新能源负荷、储能运行数据，建立储能参与电网削峰填谷的优化目标函数及其相关约束，并提出削峰填谷评价指标体系，搭建“新能源+储能”优化调度模型，并进行仿真分析及验证。

2.1 目标函数

对电网负荷削峰填谷的主要目的是减小高峰时的负荷，增大低谷时的负荷，保证负荷的平稳，减小常规机组的启停，同时也可延缓系统装机容量的投入，也有利于减少变压器和线路上的电能损耗，达到节能降损的目的[8-9]。而降低负荷的高峰，抬高负荷的低谷，保证负荷的平稳，则可通过负荷标准差进行衡量，标准差越小，负荷越平稳。

以负荷标准差来表征负荷削峰填谷的效果能够更直观地反映负荷的平稳程度，同时负荷标准差越小，峰谷之间的差距也越小，从而达到削峰填谷的目的。本文考虑将储能电站并入电网后负荷标准差最小为目标，构建储能参与电网削峰填谷优化目标函数，其数学表达式如下：

式中：Pl,t为第t时刻的实际县域东南部电网统调负荷；Pb为目标函数优化对象变量的向量形式，即储能电站优化周期内对外充放电功率构成的向量；Pb,t为第t时刻储能电站的充放电功率，T为负荷采样周期，指采样的个数，并不是时间长度；Pa为储能放电或充电后的负荷平均值。

2.2 优化约束条件

在优化调度模型中，由于不考虑电网的拓扑结构，只须要考虑储能参与电网削峰填谷相关物理约束产生的约束条件即可。

2.2.1 储能充放电功率约束

储能电站充电时：Pch,max≤Pb,t≤0。

储能电站放电时：0≤Pb,t≤Pdis,max。

式中：Pch,max为储能电站最大充电功率；Pdis,max为储能电站最大放电功率。

2.2.2 储能剩余电量约束

储能储存电能的能力有限，因此储能充放电时还须要考虑其容量大小。储能的容量计算公式如下：

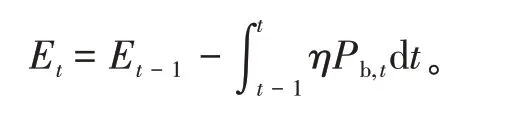
式中：Et为t时刻储能电站所储存的能量；η为充电系数。

2.3 评价指标

对储能参与电网削峰填谷的不同控制策略进行评价，构造削峰填谷效果评价指标，以绝对峰谷差、峰谷系数、峰谷差率作为负荷极值相关运算的评价依据。

2.3.1 绝对峰谷差

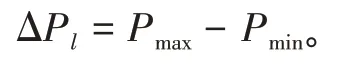
式中：Pmax为负荷最大值；Pmin为负荷最小值。负荷绝对峰谷差ΔPl指标表征在一定时间尺度下，负荷最大绝对偏差，负荷绝对峰谷差越小则负荷最大，绝对偏差越小。

2.3.2 峰谷系数

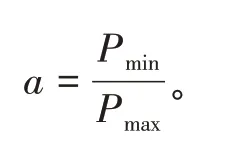
式中：负荷峰谷系数a表征在一定时间尺度下负荷曲线平坦程度，负荷峰谷系数越大，负荷曲线越平坦。

2.3.3 峰谷差率

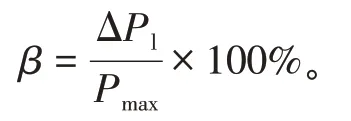
式中：负荷峰谷差率β表征在一定时间尺度下负荷波动程度，负荷峰谷差率越小，负荷波动范围越小。

2.4 二次规划算法

本文基于二规划算法构建“新能源+储能”优化调度模型。二次规划问题是最简单而又最基本的约束非线性规划问题，其目标函数是二次函数，约束都是线性等式或不等式[10-12]。标准的二次规划数学模型如下：

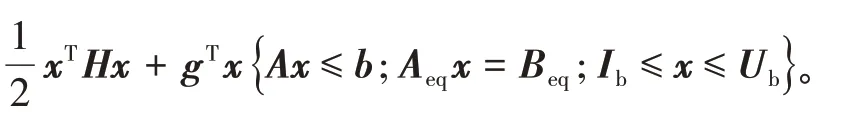
式中：A，Aeq分别为不等式约束与等式约束矩阵；b、Beq、Ib、Ub、g、x均为向量；H为二次型矩阵。

3 算例仿真和分析

某县域东南部属风、光等新能源富足地区，拥有35 kV风电电站1座，总装机容量22 MVA；35 kV光伏电站2座，总装机容量50 MVA；10 kV光伏电站11座，总装机容量28.26 MVA，同时包含一定数量的用户侧低压光伏电站。某县域电网侧储能电站的参数数据，如表1所示。

表1 储能电站参数数据

基于MATLAB仿真平台，运用二次规划算法构建“新能源+储能”优化调度模型，开展计及新能源消纳的储能电站充放电策略仿真分析研究。随机选取四个季度中的一天作为典型负荷日，在不同负荷场景下，验证本文所提出的优化模型的正确性及可推广。

场景1：第一季度选取典型负荷日。

场景2：第二季度选取典型负荷日。

场景3：第三季度选取典型负荷日。

场景4：第四季度选取典型负荷日。

3.1 不同场景下负荷曲线

选取不同负荷场景下某县域东南部地区负荷及新能源出力作为基础数据，如图3所示。

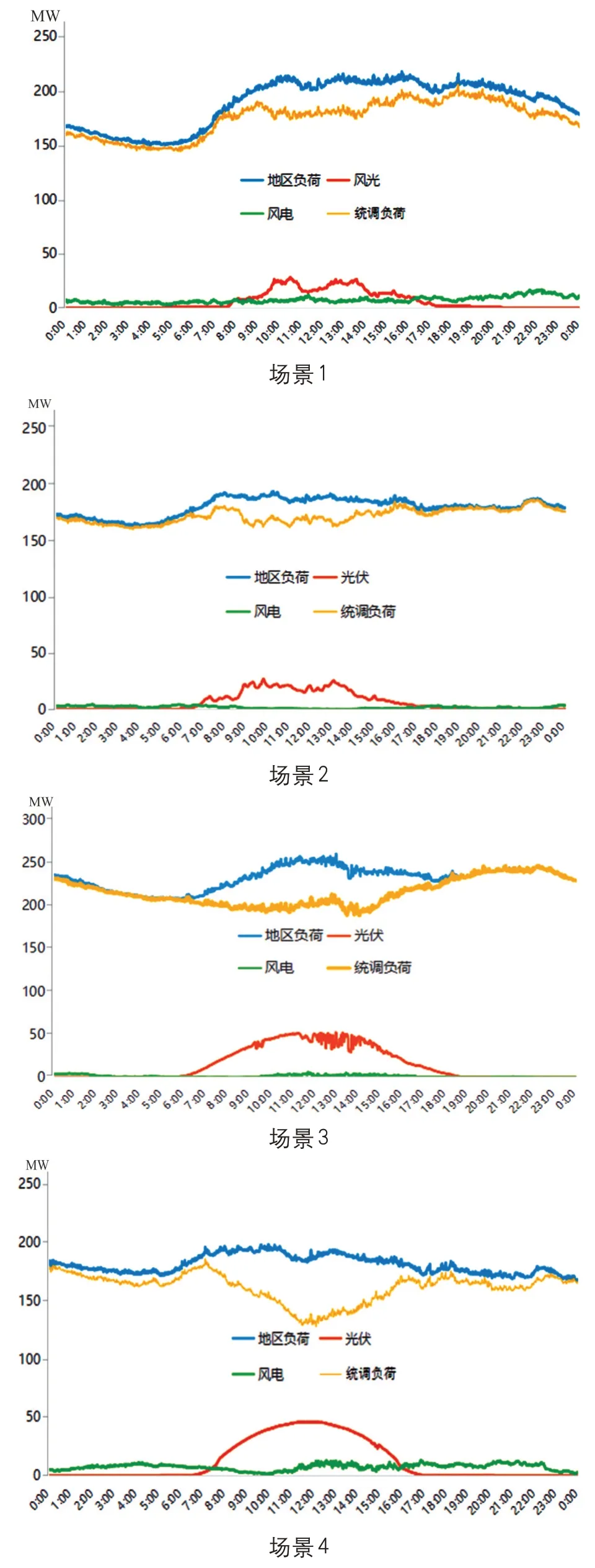
图3 不同场景下地区负荷及新能源出力

3.2 不同场景下仿真结果

选取四个季度的典型负荷日，利用储能对区域电网统调负荷曲线进行削峰填谷优化控制，基于MATLAB仿真平台的“新能源+储能”优化调度模型仿真结果，如图4、图5所示。

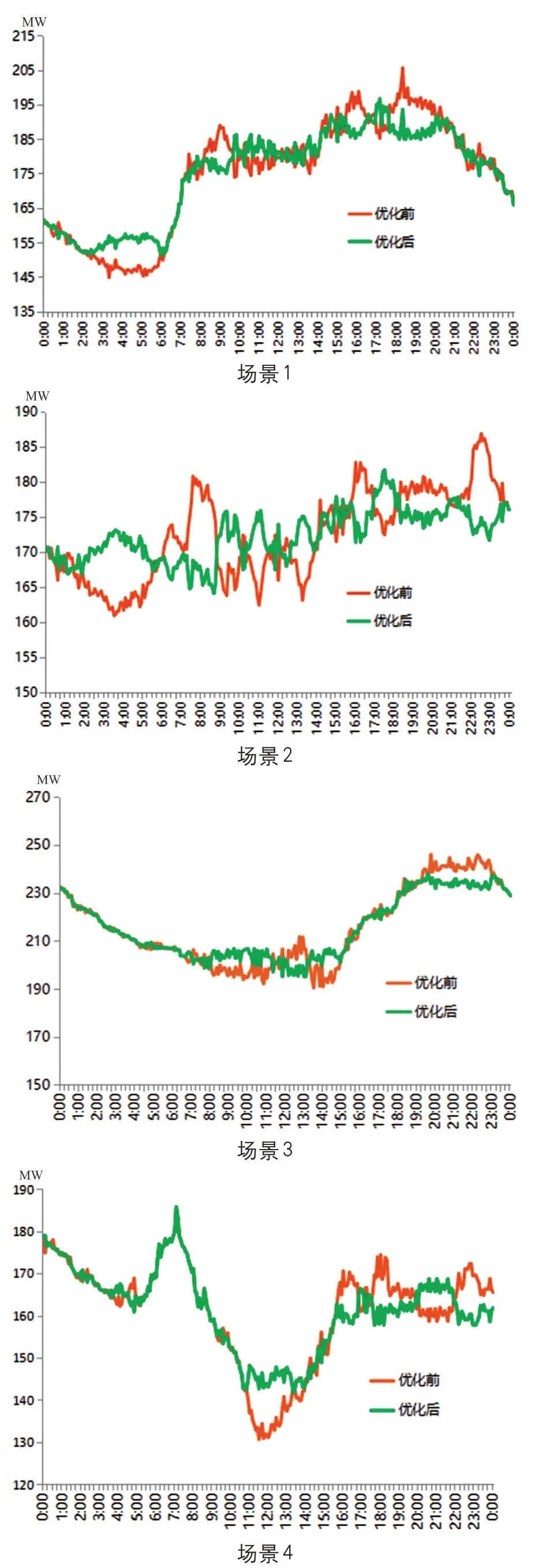
图4 不同场景下统调负荷曲线

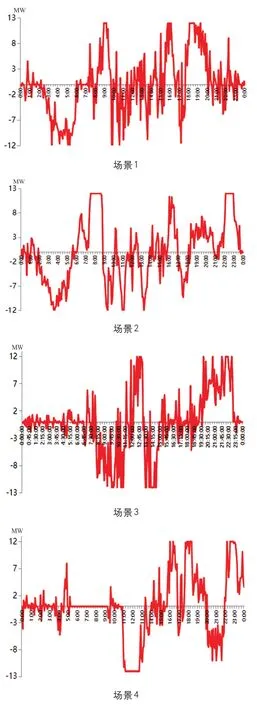
图5 不同场景下储能充放电曲线

综合上述各负荷场景，本文所提出的优化调度模型在各季度典型负荷日下仿真结果理想，就目前储能运行数据而言，相比于恒功率的储能充放电策略，在考虑新能源消纳的前提下，优化后的储能柔性充放电策略对某县域东南部地区统调负荷曲线削峰填谷效果明显，同时对蓄电池等设备具有更好地保护作用，可以进一步发挥储能电站综合效益，缓解储能电站性能的恶化，有效延长蓄电池的循环寿命，能够更大程度地保证储能电站安全、可靠、稳定运行[13-15]。

场景1：一季度负荷基数较低，风光等新能源出力一定程度上起到对调负荷曲线调峰的作用。在此基础上，利用储能对统调负荷曲线进行削峰填谷优化控制，进一步平抑优化统调负荷曲线，缓解常规机组的调峰压力。

场景2：二季度典型日负荷基数较低，风光等新能源出力波动较大，造成统调负荷曲线波动加大，从而也加大了储能电站平抑优化负荷曲线的难度，通过动态调整储能电站充放电策略，一定程度上能够平抑优化统调负荷曲线。

场景3：三季度典型日负荷基数较大，在风光出力较为稳定的情况下，新能源并网发电能够起到一定的调峰作用[16]，在此基础上，利用电网侧储能对统调负荷曲线进行削峰填谷优化控制，进一步平抑优化统调负荷曲线。

场景4：四季度典型日负荷基数较小，在风光等新能源出力较为稳定的情况下，新能源并网发电会出现反调峰现象，在此基础上，利用电网侧储能对统调负荷曲线进行削峰填谷优化控制，进一步平抑优化统调负荷曲线，缓解常规机组的调峰压力。

3.3 不同场景下指标分析

根据本文所建立的储能削峰填谷评价指标，在四个季度典型负荷日下，储能优化前后指标数据对比，如表2所示。

由表2对比结果，表明储能充放电策略优化后，各季度典型日统调负荷曲线削峰填谷效果明显，可有效减小负荷高峰值，增加负荷低谷值，一定程度上缓解了常规机组的调峰压力。

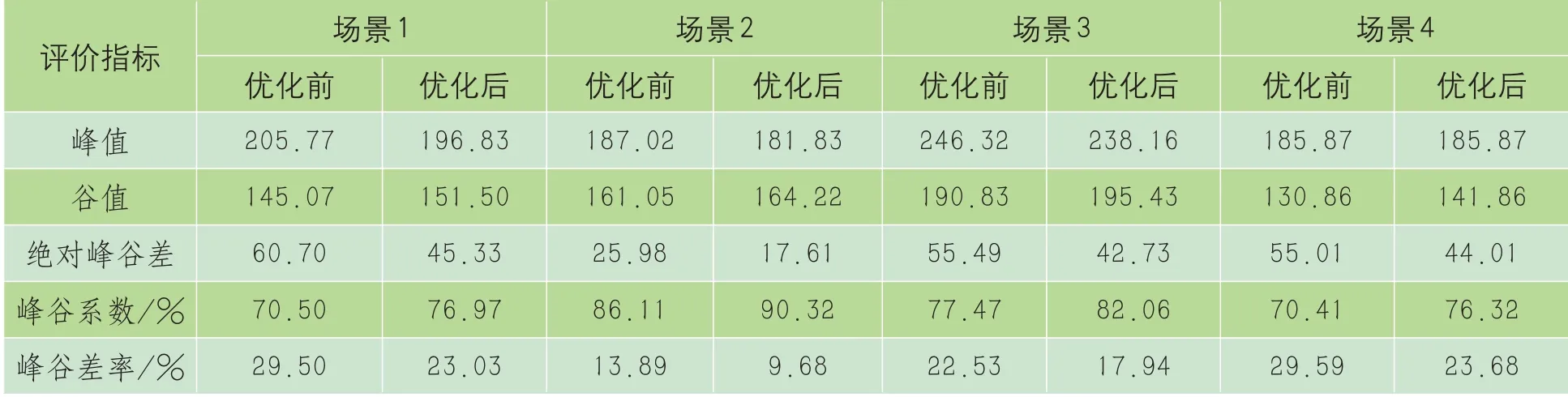
表2 各场景下储能优化指标对比 MW

3.4 不同场景下经济性分析

本文采用《浙江省电网销售电价表》中大工业用电、一般工商业及其他用电、农业生产用电六时段分时电价（电价时段划分：尖峰时段19:00—21:00；高峰时段8:00—11:00、13:00—19:00、21:00—22:00；低谷时段11:00—13:00、22:00—次日8:00），作为储能充放电优化策略经济性评价的电价依据，如图6所示。

图6 六时段分时电价曲线

选取各季度典型负荷日储能电站充放电数据，计算典型负荷日储能充放电优化策略下的购电成本和售电收益，如图7所示。

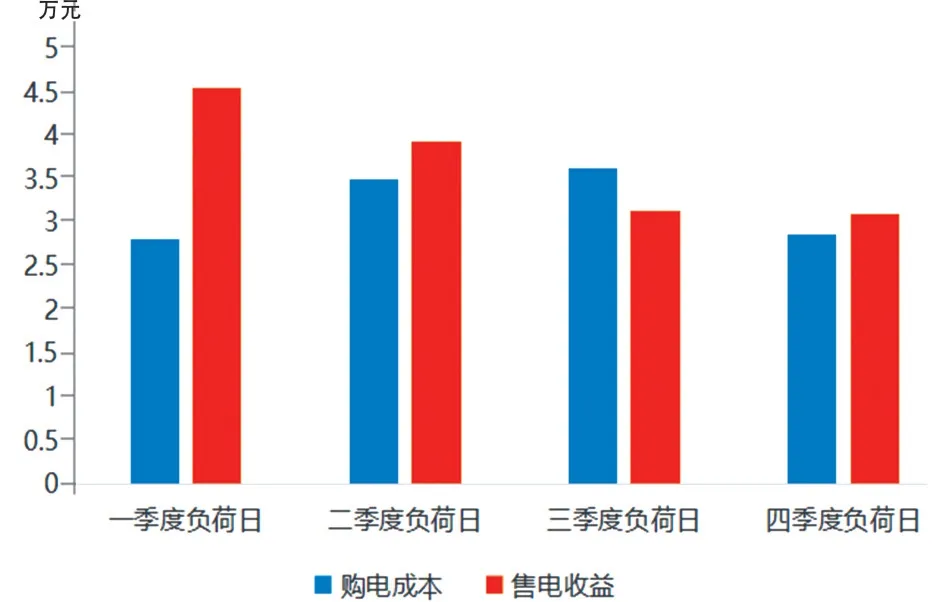
图7 典型负荷日经济性评价

由图7可知，在大多数情况下储能电站能够实现盈利，而在三季度典型负荷日下，出现购电成本大于售电收益的情况。原因是三季度典型负荷日下，储能为了平抑优化统调负荷曲线，其充电时间多集中在高峰电价时段（8:00—11:00、13:00—15:00两个时段），而在低谷电价部分时段，储能电站处于放电模式。说明本文提出的“新能源+储能”优化调度模型仅仅着重于考虑新能源消纳的储能电站优化调度，一定程度上不具有经济性[17-18]。后续考虑将储能充放电经济性因素加入到优化调度模型当中，进一步优化模型的经济性指标。

4 模型应用流程

在区域电网新能源预测准确率较高的前提下，可以通过本文提出的“新能源+储能”优化调度模型，对东南部电网统调负荷曲线进行平抑优化调度，缓解新能源反调峰带来的压力，提升区域电网新能源发电的可控性和渗透率。“新能源+储能”优化调度模型应用的具体流程，如图8所示。

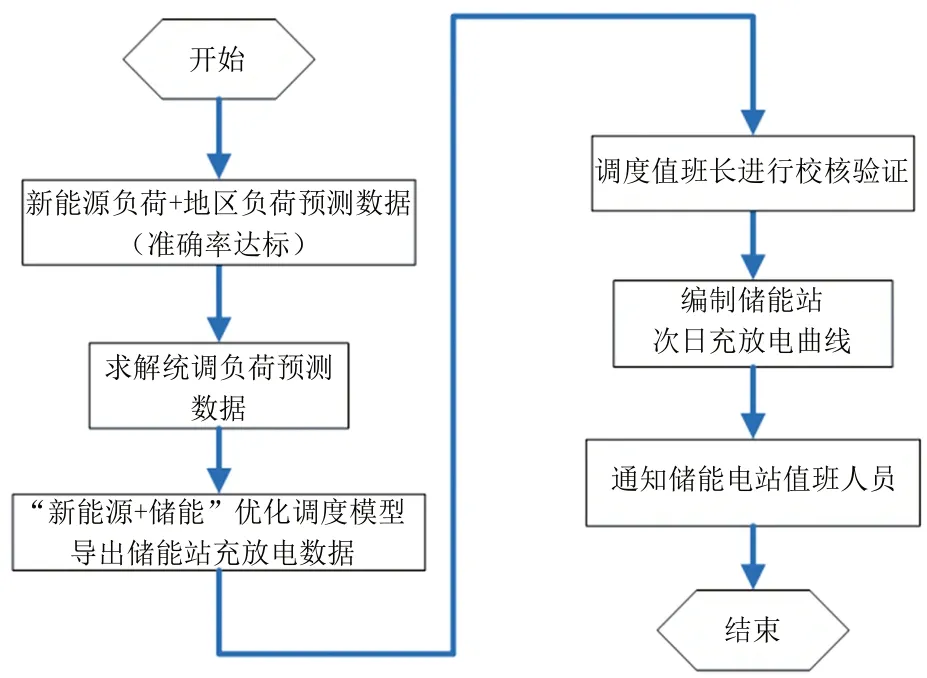
图8 模型实际应用流程

由图8所示，“新能源+储能”优化调度模型应用流程为：通过前一日对某县域东南部地区新能源负荷及地区负荷进行精准预测，进而求解出东南部地区的统调负荷预测数据。将预测结果作为输入数据代入本文提出的“新能源+储能”优化调度模型，导出储能电站次日充放电数据，再由调度值班长进行校核验证，确认后编制次日储能电站充放电曲线，并告知储能电站运维人员，次日按照编制的储能充放电曲线进行实际应用。

5 结束语

综合考虑电网调峰、系统备用容量充裕性和新能源利用率等因素[19]，本文根据县级电网东南部负荷特性以及储能运行数据，积极开展计及新能源消纳的电网侧储能削峰填谷优化策略研究，并提出储能参与电网削峰填谷评价指标体系，所构建的“新能源+储能”优化调度模型能够有效平抑优化统调负荷曲线，削减电网负荷峰谷差，缓解常规机组的调峰压力，进一步提升电网风电、光伏等新能源发电的可控性和渗透率。

本文研究成果表明，如果新能源并网消纳目标过高，单纯通过电网侧储能来满足新能源消纳的要求，一定程度上不具有经济性，应该考虑采取多种灵活性措施进一步提升电网新能源消纳水平。

目前，本文研究成果已取得了初步成效，为进一步发挥储能电站的综合效益，提升储能电站的综合运行指标，以及下阶段优化储能调控规范化管理夯实了基础，也为全国电化学储能电站调控运行提供了一定的经验参考。