数学文化视角下2022年高考试题研究

常海斌，曲元海，陈霖，邵鹏

抽象、推理和模型是数学赖以发展的基本思想［1］，抽象的特殊性、推理的严谨性、模型的一般性使得数学常给人一种文化自由、价值无涉的感觉.直至20世纪60年代，数学文化的概念才被首次提出，而后美国数学家怀尔德在其著作《数学概念进化》和《作为系统的数学》中系统提出了数学——作为一种文化体系的观点［2］.1988年，以“数学·教育·社会·文化”为主题的ICME-6在匈牙利首都布达佩斯召开，这次大会的召开使得数学文化受到了数学教育界的广泛关注［3］.所谓数学文化是指数学的思想、精神、方法、观点、语言，以及它们的形成与发展.广义上还包括数学家、数学史、数学美、数学教育、数学发展中的人文成分、数学与社会的联系、数学与各种文化的关系等等［4-5］，其对于学生心理品质和诚信观的塑造、审美能力的培养及思维的训练等具有重要意义［6］.

数学文化作为高考数学所考查的四大学科素养目标之一［7］，近年来受到越来越多学者的关注.王婷、李祎［8］和孙庆括［9］分别从不同视角对近十年高考数学文化命题的特征进行了分析；张维忠和金月丹以近五年的高考数学试题为研究对象，对其中数学文化类考题的内容类型和运用水平进行了研究［10-11］.祁平［5］和张浩［12］等人分别对数学文化类试题的编制策略进行了探讨.高考作为教育教学的指挥棒，具有重要的正面导向作用［13］，本文以2022年的8套高考数学试题为研究对象，对其中数学文化类考题的特征进行剖析，以期为数学文化类试题的编制和教师教学提供借鉴与参考.

1 数学文化试题特征分析

以下从题型与题号、数学文化的融入方式、文化背景、文化类型及考查的内容领域五个方面对全国甲卷（文科、理科）、全国乙卷（文科、理科）、新高考Ⅰ卷、新高考Ⅱ卷、北京卷、浙江卷八套试卷中的数学文化类考题进行分析.基于已有研究，将数学文化的融入方式划分为可分离型和不可分离型［12］，将数学文化的类型划分为知识源流、学科联系、社会角色、审美娱乐、多元文化五类［14］.具体情况如表1所示.

从表1可以看出，2022年高考数学对数学文化的考查具有以下几点特征.第一，从考查题型的角度来看，数学文化类考题主要以选择题（单项选择题）的形式进行考查，以解答题和填空题形式考查的较少，其中只有浙江卷以填空题的形式进行了考查.研究表明［15］，一份数学试题中，解答题难度最大，填空题次之，选择题难度最低.由此可见，从考查题型的角度来看，数学文化类考题的难度整体较低，还有进一步均衡和完善的空间.第二，从数学文化的融入方式来看，绝大多数考题都选择了“不可分离型”的融入方式，选择“可分离型”的试题仅有2道，这说明命题人非常重视数学文化与问题的深度融合，而不是将数学文化强加于考题之中.第三，试题的文化背景十分丰富，垃圾分类、南水北调、北京冬奥、航天工程、数学史等内容在考题中均有呈现，这对于学生体会数学的文化属性和应用价值具有重要意义.第四，通过对试题中的文化主题进行分析，可以发现“社会角色”主题下的考题最多，共计有七道.“知识源流”主题下的考题有两道，“审美娱乐”主题下的考题仅有一道，而“学科联系”和“多元文化”类的考题并未出现，可见考题在不同文化主题下的分布还不够均衡.第五，从考查的内容领域来看，“函数”“几何与代数”“统计与概率”这几条主线中的知识点均有所考查，且“统计与概率”主线下的知识考查最多，而“数学建模活动与数学探究活动”并未涉及.

表1 2022年数学高考中数学文化类考题统计

2 试题欣赏与评析

2.1 以优秀传统文化为背景，树立民族文化自信

例1（新高考Ⅱ卷第3题）中国古建筑不仅是挡风遮雨的住处，更是美学与哲学新知识的体现.图1是某古建筑物的剖面图，AA'，BB'，CC'，DD'是桁，DD1，CC1，BB1，AA1是脊，OD1，DC1，CB1，BA1是相等的步，相邻桁的举步的比分别为，已知k1，k2，k3成公差为0.1的等差数列，且直线OA的斜率为0.725，则k3=（）.

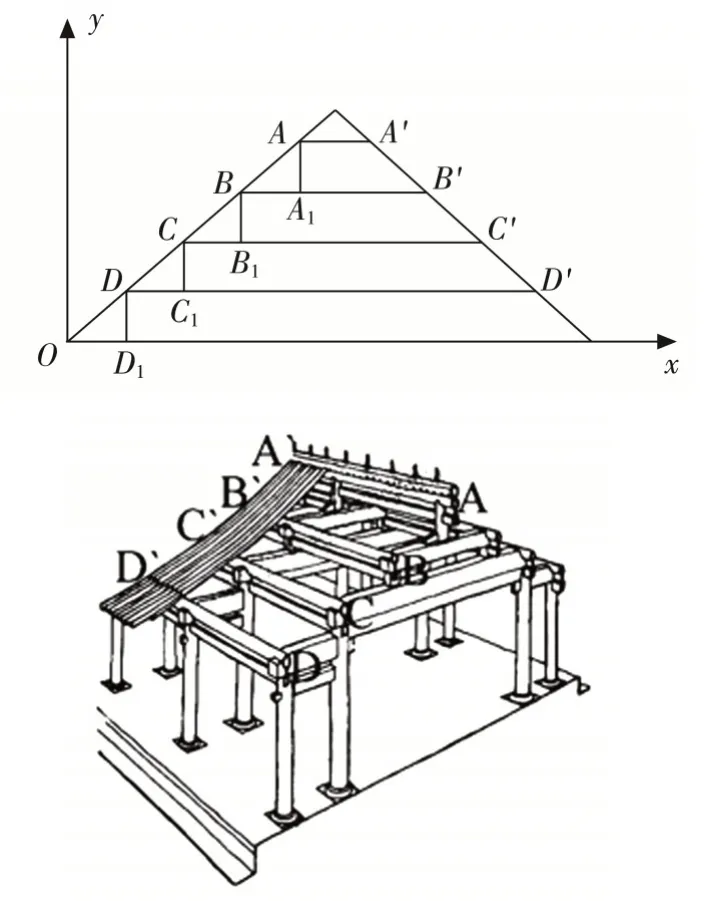
图1 古建筑物剖面图

A.0.75 B.0.8 C.0.85 D.0.9

点评：我国古代建筑具有悠久的历史和辉煌的成就，这些古建筑体现了数学的简洁之美、对称之美、周期之美、和谐之美，展现了我国古代高超的建筑水平和精益求精的工匠精神.本题以我国古代建筑中的举架结构为背景，考查学生利用等差数列和三角函数等知识解决实际问题的能力.设OD1=DC1=CB1=BA1=1，则CC1=k1，BB1=k2，AA1=k3，易知k3=k1+0.2=k2+0.1，结合=0.725，易得k3=0.9.通过本题，可以让学生了解我国古代建筑的辉煌成就，体会数学在建筑中的应用，感悟数学美的韵味.

例2（浙江卷第11题）我国南宋数学家秦九韶，发现了从三角形三边求面积的公式，他把这种方法称为“三斜求积”，如图2所示.它填补了我国传统数学的一个空白.如果把这个方法写成公式，就是其中a，b，c是三角形的三边，S是三角形的面积.设某三角形的三边a=，b=，c=2，则该三角形的面积S= .

图2 三斜求积术

点评：“三斜求积术”是我国南宋时期杰出数学家秦九韶独立提出的一种利用三角形三边长直接求三角形面积的方法，这一方法填补了中国数学史中的一个空白，彰显了我国古代数学的高超水平.该公式最早出现在海伦的著作《测地术》中，因此也被称为海伦公式.此题以“三斜求积术”为背景，主要考查学生数学运算素养，由于本题已给出三角形的三边长及面积计算公式，学生只需将数值代入公式即可求得.本题也可利用余弦定理求出sinA(sinB、sinC)，进而利用公式求得答案.整体而言，本题难度较低，但学生可以通过本题了解我国古代数学的辉煌成就，对于树立文化自信具有重要意义.

2.2 以科技发展与进步为背景，坚定投身祖国建设的青春信念

例3（全国乙卷理科第4题）嫦娥二号卫星在完成探月任务后，继续进行深空探测，成为我国第一颗环绕太阳飞行的人造卫星.为研究嫦娥二号绕日周期与地球绕日周期的比值，用到数列，…，依 此 类 推，其 中ak∈N*(k=1,2,…)，则（）.

A.b1＜b2B.b3＜b8C.b6＜b2D.b4＜b7

点评：近年来，我国航天事业发展迅速，正一步步向航天强国不断迈进.嫦娥二号是我国探月计划中的第二颗人造卫星，是我国走向航天强国的重要一步，它以我国古代神话人物嫦娥命名，展现了我国航天人的极致浪漫和文化自信.本题以此为背景，考查学生运用数列、函数、不等式等基础知识分析问题和解决问题的能力，同时引导学生关注我国航天事业的发展，激发学生的爱国情怀和民族自豪感.本题可以采用取特殊值的方法来解决，取an=1，易得可见分子分母分别构成斐波那契数列，所以b5、b6、b7、b8易求，该题得解.

例4（北京卷第7题）在北京冬奥会上，国家速滑馆“冰丝带”使用高效环保的二氧化碳跨临界直冷制冰技术，为实现绿色东奥做出了贡献，图3描述了一定条件下二氧化碳所处的状态与T和lgP的关系，其中T表示温度，单位是K；P表示压强，单位是bar.下列结论中正确的是（）.

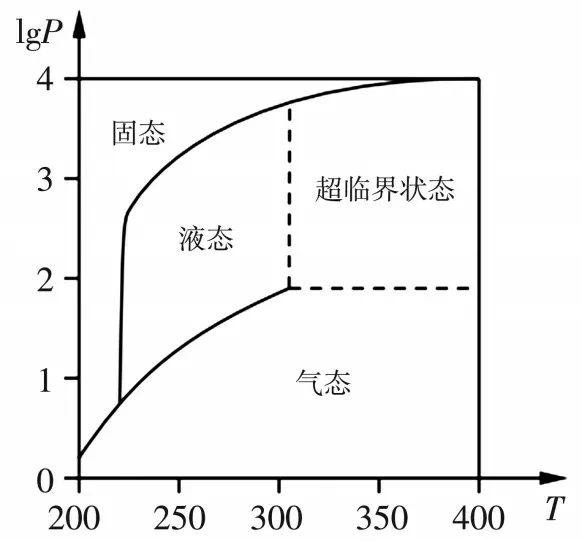
图3 二氧化碳所处状态与T和lgP的关系图

A.当T=220，P=1026时，二氧化碳处于液态.

B.当T=270，P=128时，二 氧 化 碳 处于气态.

C.当T=300，P=9 987时，二氧化碳处于超临界状态.

D.当T=360，P=729时，二 氧 化 碳 处于超临界状态.

点评：2022年2月4日，北京冬奥会 在 国家体育场开幕，北京也成为世界上首个“双奥之城”.本次冬奥会首次采用了清洁低碳的二氧化碳跨临界直冷制冰技术，这是目前世界上最环保的制冰技术，是我国又一重大技术突破.本题以二氧化碳跨临界直冷制冰技术为背景，主要考查学生对数的相关知识和图象分析能力.当T=360，P=729时，lgP=lg729＞2，分析图象可知此时二氧化碳处于超临界状态，故选择D项.本题考查难度较低，数学文化的渗透让学生了解二氧化碳跨临界直冷制冰技术，坚定奉献科技事业、投身祖国建设的青春信念.

2.3 以经济社会发展为背景，普及民生工程知识

例5（新高考Ⅰ卷第4题）南水北调工程缓解了北方一些地区水资源短缺问题，其中一部分蓄入某水库，已知该水库水位为海拔148.5 m时相应水面的面积为140 km2；水位为海拔157.5 m时，相应水面的面积为180 km2.将该水库在这两个水位间的形状看做一个棱台，则该水库水位从海拔148.5 m上升到157.5 m时，增加的水量约为（7≈2.65）（），如图4所示.

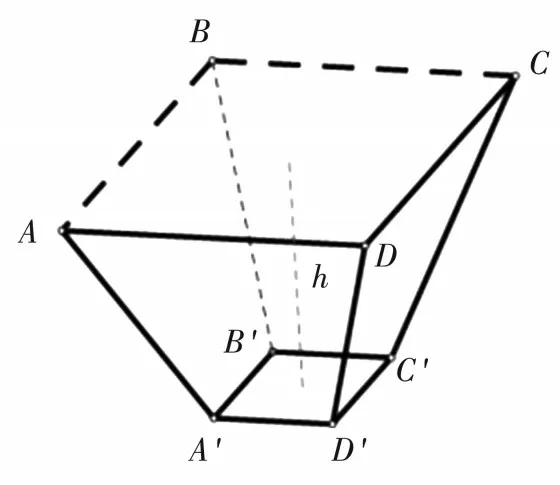
图4 水库水位示意图

A.1.0×109m3B.1.2×109m3

C.1.4×109m3D.1.6×109m3

点评：南水北调是我国的战略性工程，也是一项重要的民生工程，超1.2亿人从这项工程中直接受益.通过这项工程的开展，使广大北方地区的供水格局得以保证和优化，同时也推动了沿线生态文明建设和经济社会发展.本题以“南水北调工程”为背景，着重考查学生空间想象、数学运算等素养.如图4所示，设棱台的上、下底面面积分别为S和S'，高为h，由题意可知，S=180 km2，S'=140 km2，h=157.5 m-148.5 m=9 m.由棱台体积公式易得该棱台体积（即增加的水量）约为1.4×109m3，故选择C项.

例6（全国甲卷理科第2题）某社区通过公益讲座以及普及社区居民的垃圾分类知识，为了解讲座效果，随机抽取10位社区居民，让他们在讲座前和讲座后各回答一份垃圾分类知识问卷，这10位社区居民在讲座前和讲座后问卷答题的正确率如图5所示，则（）.

图5 讲座前后答题正确率情况

A.讲座前问卷答题的正确率的中位数小于70%.

B.讲座后问卷答题的正确率的平均数大于85%.

C.讲座前问卷答题的正确率的标准差小于讲座后正确率的标准差.

D.讲座后问卷答题的正确率的极差大于讲座前正确率的极差.

点评：绿水青山就是金山银山，垃圾分类是一项“利国利民”的民生工程.通过垃圾分类，不仅可以减少环境污染、降低处理成本，而且可以变废为宝，增加收益.本题以“垃圾分类”为背景，主要考查学生利用中位数、平均数、标准差和极差等相关知识进行数据处理的能力.由图5可知，讲座后问卷答题的正确率的平均数为89.5%＞85%，故选择B项.

3 启示与建议

通过对试题总体特征的分析，以及部分试题的赏析，发现了一些命题特征，基于此为试题的编制和教师教学提出以下几点建议.

3.1 教师应努力夯实自身的数学文化底蕴，深入挖掘数学文化类考题的文化背景

每一道数学文化类考题都蕴含着丰富的文化背景，这些文化背景对于开阔学生的数学视野、提升学生的人文素养具有重要意义.教师应努力夯实自身的数学文化底蕴，在教学过程中深入挖掘数学文化类考题的文化背景，引导学生感悟数学的文化魅力.这就要求数学教师要深刻理解数学知识的发生发展脉络，以此为基础不断汲取数学文化知识，促进自身的专业化发展.例如，2022年全国甲卷理科第8题考查了《梦溪笔谈》中的“会圆术”，《梦溪笔谈》是一部科学史著作，其作者是我国古代著名科学家沈括，教师除了要积累这些题目中的已有信息外，还要以此为契机深入了解沈括的其他贡献，如“隙积术”等.只有这样，教师才能不断提高自身的数学文化素养，促进自身的专业化发展.

3.2 促进数学文化教育前移，提高学生的数学核心素养和人文素养

学生身心发展的特点决定了数学核心素养发展的阶段性.例如，数据分析作为数学的六大核心素养之一，在小学阶段，由于学生数学思维的发展还不够成熟，因此我们的重点是培养学生的数据意识，到了初中阶段我们希望学生通过数学课程的学习获得一定的数据观念，而到高中阶段才要求学生具有一定的数据分析能力.数学文化作为发展学生核心素养的重要途径，其对于义务教育阶段学生的发展同样具有重要作用.宋乃庆教授认为［17］：数学文化在激发小学生的数学兴趣和情感，发展学生的学习能力、实践能力和创新能力等方面具有重要价值.因此，数学文化教育应前移至义务教育阶段，从头抓起、从小抓起，让学生在数学文化的熏陶中发展自己的理性思维，提高自身的数学核心素养和文化素养.

3.3 进一步丰富考题中的文化类型，着重彰显中华优秀传统文化

2022年高考数学主要涉及“社会角色”“知识源流”和“审美娱乐”这三种文化类型，而“多元文化”和“学科联系”这两种文化类型的考题并未涉及.多元文化类考题有助于学生开阔眼界，体会精彩纷呈的数学文化，而“学科联系”类考题有助于学生体会数学的应用价值，了解数学与其他学科之间的联系，因此，数学文化类考题应进一步丰富文化的类型.例如，2022年浙江卷第11题考查了秦九韶的“三斜求积术”，彰显了我国古代数学的高超水平，但是在数学发展的历史长河中，阿基米德和海伦也曾对这一课题进行过深入研究，因此本题在着重考查“三斜求积术”的同时也可以对阿基米德和海伦的贡献进行简单介绍，让学生穿越历史时空，体会中西方数学家的智慧.此外，考题中还要进一步增加“中华优秀传统文化”的比重，关于《完善中华优秀传统文化教育指导纲要》中明确提出：要把中华优秀传统文化教育系统融入课程和教材体系，同时增加中华优秀传统文化内容在中考、高考升学考试中的比重［16］，高考作为“教师教”与“学生学”的指挥棒，对于中华优秀传统文化的传播与普及具有重要意义，因此，考题应进一步彰显中华优秀传统文化，培养学生的爱国情怀与民族自豪感.

3.4 进一步均衡数学文化在不同内容领域的考查，同时丰富数学文化的考查形式

“函数”“几何与代数”“统计与概率”和“数学建模活动与数学探究活动”是高中数学课程的四大主线.从考查的内容领域来看，2022年数学文化类考题对“函数”“几何与代数”“统计与概率”这几条主线中的知识点均有所考查，且“统计与概率”主线下的知识考查最多，而“数学建模活动与数学探究活动”并未涉及.模型作为数学与外部世界沟通的桥梁，对于学生创新能力和实践能力的提升具有重要意义.在今后的试题编制过程中，应增加以各种模型为背景的考题，如考虑利用Cobb—Douglas生产函数模型、Keynesia模型等进行试题编制.此外，还应增加数学文化的考查形式，目前绝大多数数学文化类考题都以单项选择题的形式考查，而以多项选择题、填空题、解答题等形式考查的较少，这不利于数学文化与考查内容的深度融合，数学文化的考查形式也应趋于多元化.

4 结语

新高考背景下，数学科的考查目标与考查要求均有所变化，数学文化作为高考数学所考查的基本学科素养目标之一，是提高学生人文素养，增强学生文化自信的重要依托.我们对数学文化的态度不应停留在“高评价，低运用”的层面，要切实挖掘数学文化的育人功能.本文对2022年高考中的数学文化进行了深入剖析，发现了一些命题特征，基于此为一线教师教学提供了几点可操作性建议.本研究既具有一定的现实指导意义，同时也为科研人员的理论研究提供了参考与借鉴.