右端不连续免疫对非线性出生率和医院容纳的影响
2022-11-22李迅陶龙
李迅,陶龙
在人类漫长的发展历程中,传染病始终是妨碍人类社会文明发展的阻碍之一,也是危害人类生命健康安全的最大因素之一.尽管是在医学、科学文明高度发展的今天,SARS、埃博拉病毒、COVID-19等仍然会爆发传染,极大地威胁了人类社会的安全和发展.人类历史上产生了许多研究传染病的方法,其中数学家们发现可以建立微分方程动力系统数学模型进行定性和定量研究.影响较大的是ERMACK等研究发明的流行症仓室模型[1].随着微分动力系统理论的日益发展,模型中考虑的现实问题因素也越来越多,专家学者们也取得了更多符合现实意义的研究成果[2-3].文献[4]开始考虑医治因素有限对传染病的影响,发现医治因素对疾病传染的稳定性具有重要影响;在现实生活中医院的物资、空间、医护人员都是有限的,医院不可能接收全部病人,因此文献[5]考虑了医院容纳和非线性出生率对仓室模型的影响,并取得了具有现实意义的重要结论.
尽管如此,目前对于非线性出生率和医院容纳量的数学模型大都是连续的微分动力系统,通常在病毒传播的早期,人们对病毒的预防和医治不够及时,导致病情得不到充分医治甚至是没有医治;经过一段时间的社会面传染,人们意识到病毒传播的严重程度后就会开始加大医治的力度,由此会形成一个较大的患者人数间断变化.纵观整个过程,动力学模型应是一个不连续的微分动力系统,而不是连续的.因此本文考虑在文献[5]的研究基础上引入非连续的治疗项进行研究,实际上目前许多经典传染病系统模型中已经引入了非连续免疫治疗[6].
1 模型的建立
针对文献[5],建立如下模型:

其中:易感染人群记为S,已感染人群记为I,住院者人群记为H,治疗后康复人群记为R,N表示人口的总数量,N=S+I+H+R;A为种群人口输入数量,B为出生率,β为感染率,γ1为感染者的自我康愈率,γ2为住院者的治愈率,γ为已感染的人去医院就医的转移率,K为医院所能收治的病人最大量,μ为自然死亡率,ε1为感染者病死率,ε2为住院者的病死率;基本再生数为.其中,函数h(I)是本文引入的非连续免疫函数.
假设1h(I)=φ(I)I,其中φ:R+→R+是分段连续且单调不递减的函数,即除了可数个孤立点{pk}外,其他点处均连续.
由于式(1)微分系统的不连续性,经典常微分理论的结论和性质对此动力系统不再适用.故对于式(2)的解需要重新定义,本文采用Filippov意义 下的解[6].Filippov解应对的是下述一类不连续的微分方程:

其中:式(2)右端的不连续函数f(t,x)关于变量t和x(t)是可测的且是局部本性有界的,即
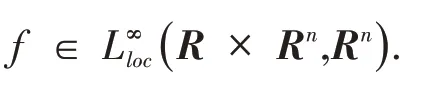
定义1对于如下形式的集值映射[7]:其 中K是 作用 在f上的 算子;xδ表 示x的δ邻 域;在函数f的连续点处,集合F(t,x)是由f(t,x)所构成的单点集,在函数f的不连续点处,则集合F(t,x)是一个凸闭集合;意味着F取集合的凸闭包;交是在所有的零测度集合N和所有的δ>0上取交集;在这种定义方式下,方程(2)的解是微分包含F(t,x)中的一个解函数
对于满足初值的Filippov解是绝对连续的向量函数,即若(S(t),I(t),H(t),R(t))是式(1)的Filippov解,则(S(t),I(t),H(t),R(t))在[0,T)上绝对连续,且函数将满足下面的微分包含:
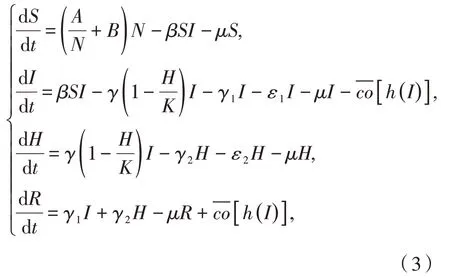
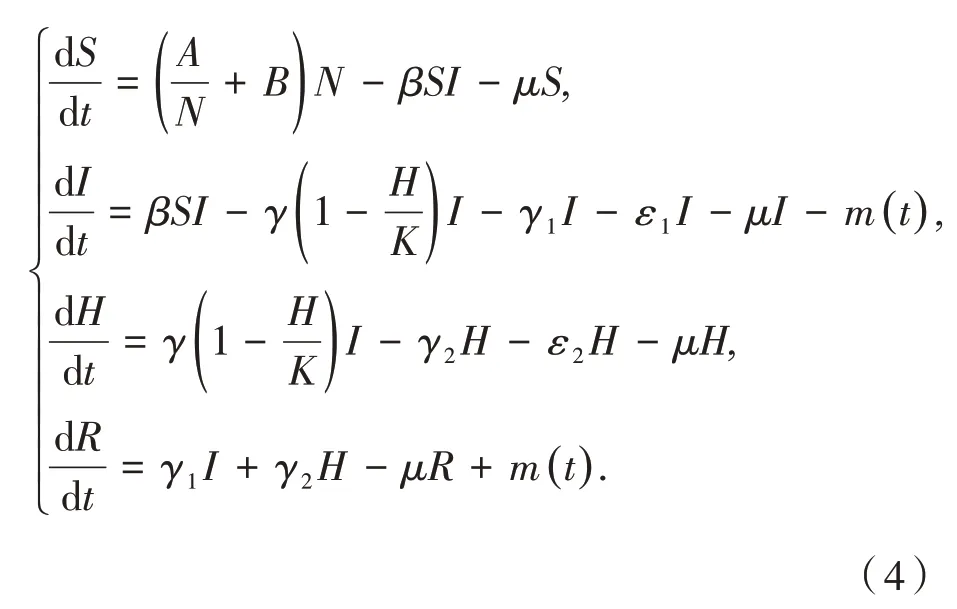
2 解的正值有界性和平衡点的存在唯一性
2.1 解的正值有界性
出于生物学现实的考虑,下面将证明模型(1)满足初值条件的解都是有界且是非负的.
命题1令(S(t),I(t),H(t),R(t))是模型(1)满足初值条件S(0)≥0,I(0)≥0,H(0)≥0,R(0)≥0的解,定义区间为[0,T),其 中T∈( 0,+∞).如若假设1成立,则对所有的t∈[0,T),有S(t)≥0且I(t)≥0且H(t)≥0且R(t)≥0.
证明 根据模型(1)在Filippov解的定义,(S(t),I(t),H(t),R(t))是微分包含式(3)的解,由式(3)中的第一个方程,可得

结合S(0)≥0可知,S(t)≥0,t∈[0,T).
命题2若假设1成立,令(S(t),I(t),H(t),R(t))是模型(1)满足初值条件S(0),I(0),H(0),R(0)∈R4+的解,则(S,I,H,R),t∈[0,T)有界.
证明由(1)可得:

综上所述,本文的可行域为:
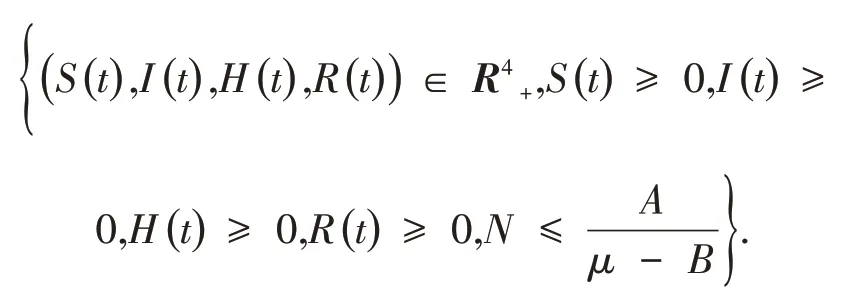
2.2 模型平衡点的存在及其唯一性
当假设1成立时,为了求解式(3)的平衡点,则需要解出下面的微分包含:


联立式(6)中的微分方程(包含),可得:

设(S*,I*,H*,R*),t∈[0,T)是模型(1)的有病平衡点,将会有下述微分包含

即若(S*,I*,H*,R*)是式(8)的平衡点,根据式(8),将存在一个常数使得μI*-ξ*.显然,这样的常数ξ*是唯一的,并且

命题3如果R0>1,那么微分包含式(6)存在唯一的正解͂,满足:
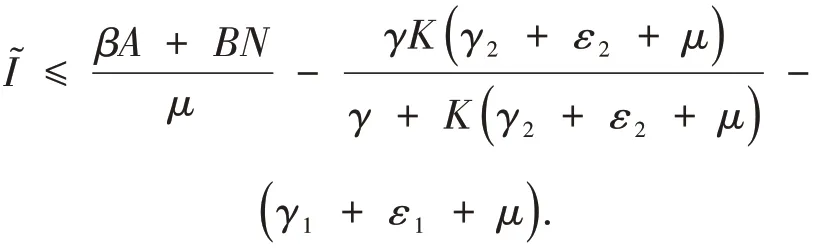
证明 首先证明式(7)微分包含解的存在性.由 于R0>1,所 以g(0)>ϕ(0)>0.另外,g(I)关于I是单调递减的,ϕ(I)关于I是单调不减的.而且,g(I)≤0当且仅当

因此,集合{I:g(I)≥φ(I+),I>0}是有界的,令那 么且
其次证明式(7)微分包含解的唯一性.为证明模型解的唯一性,先假定是微分包含式(6)的两个正解,且I1*≠I2*,由式(9)知使得

根据假设1知ϕ是非单减的函数,记f=,则有f≥0,两式相减得η1*-η2*=,从 而有η1*-η2*=对此等式两边同时除以I1*-I2*得此时,左边,右 边=,这与等式左右相等矛盾,故假设错误.命题得证.
3 有限时间的全局渐近稳定性
为不失一般性,探讨式(1)的解轨迹在有限时间内全局渐近收敛到平衡点的可能性,有必要做出下面的假设:
假设2若R0>1且φ(I)有一个跳跃间断点I*,其中I*是式(7)所确定的唯一解,且取

则根据假设2可定义:θ=min{φ+(I*)-η*,η*-φ-(I*)}>0.
定理1如果假设1和假设2均成立,则系统(1)满足初值条件S(0)≥0,I(0)≥0,H(0)≥0,R(0)≥0的所有解将在有限时间内全局渐近收敛到E*=(S*,I*,H*,R*),即 当t≥t*时,都有( S,I,H,R)=(S*,I*,H*,R*),其中:

证明令x(t)=S(t)-S*,y(t)=I(t)-I*,z(t)=H(t)-H*,w(t)=R(t)-R*,其 中根据式(4)知,存在一个可测函数η(t)∈使得式(3)变为:
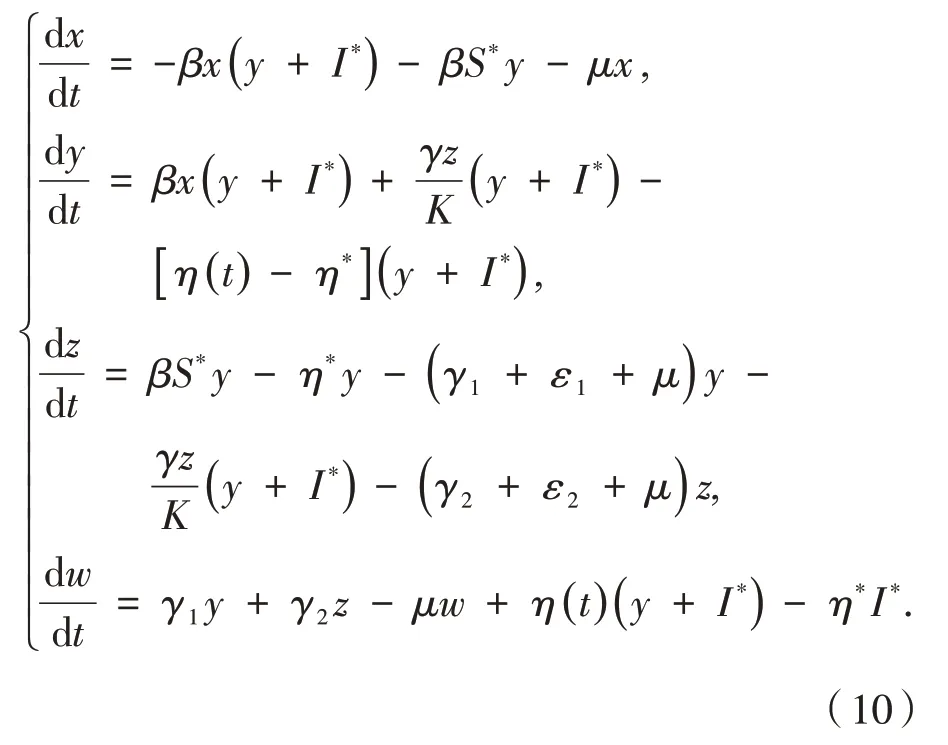
构建Lyapunov函数如下:


其中:α是一个可以在后面具体确定的正常数.容易验证V1(x(t),y(t),z(t),w(t))是关于(x,y,z,w)的正则函数.当(x(t),y(t),z(t),w(t))≠0时,V1(x(t),y(t),z(t),w(t))>0;V1( 0,0,0,0)=0;当x→+∞或当y→+∞或当z→+∞或当w→+∞时,V1(x(t),y(t),z(t),w(t))→+∞,对V1求导可得:

由假设2知,当(S(t),I(t),H(t),R(t))≠0时,[η(t)-η*]2>θ2,则对所有的t∈{t:(x,y,z,w)≠(0,0,0,0)},有

从0到t对上式进行积分得:

令
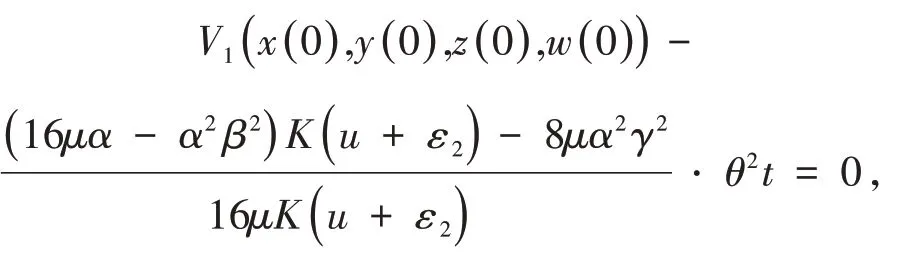
解得

即当t=t*时,
由文献[8]可知,当t>t*,则对任意的t都有V1(x(t),y(t),z(t),w(t))=0,即当t>t*时

即 当t>t*时 ,(S(t),I(t),H(t),R(t))=(S*,I*,H*,R*),定理2得证.
接下来将证明系统(1)无病平衡点的全局渐近稳定性.因假设1假定h(I)在I=0处是连续的,故不满足模型非连续的设定.需做如下的假设.
假 设3h:R+→R+,h(0)=0但h(I)在I=0处是不连续的,且至多有有限个间断点.
定理2若假设3成立,则当R0<1时,式(1)满足初值条件的解都将在有限时间内全局收敛于无病平衡点,即当

同时

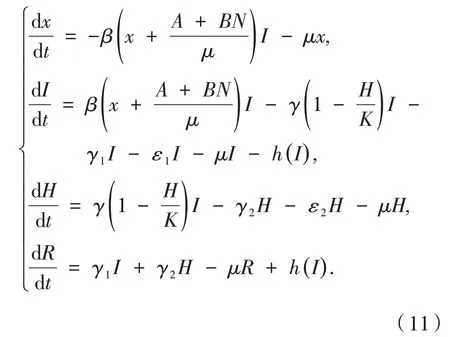
构造Lyapunov函数V2(x(t),I(t),H(t),R(t))=显然V2(x(t),I(t),H(t),R(t))是正则函数,当V2(x(t),I(t),H(t),R(t))≠0时,V2(x(t),I(t),H(t),R(t))>0且V2( 0,0,0,0)=0,由 式(4)知,对V2(x(t),I(t),H(t),R(t))求导得:

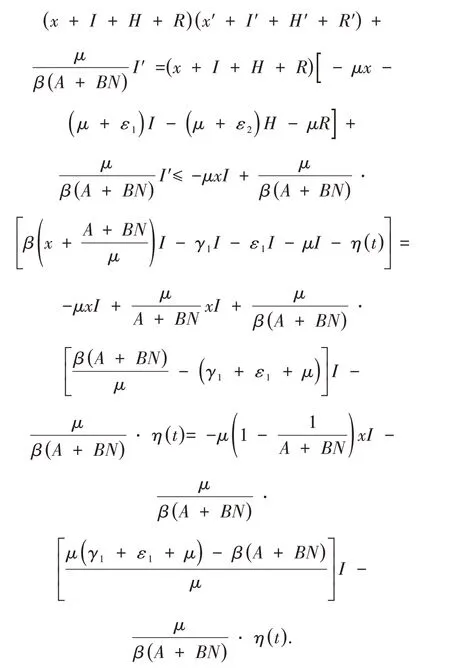
因 为A是人口输入数量,A>1且BN>0,所以;又因为R0=,所以,因此有
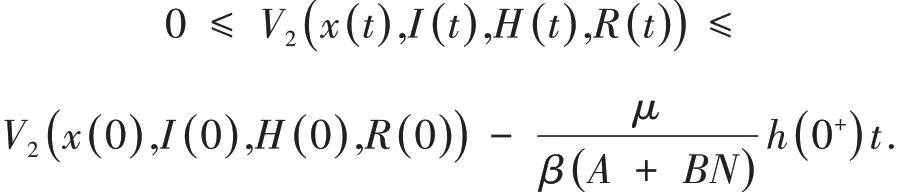
4 数值模拟
4.1 地方病平衡点的全局渐近稳定性
依据假设1,考虑选取函数h(I)=参数设定为A=20,B=0.001,N=400,β=0.03,μ=0.2,γ=0.5,K=200,γ1=0.2,γ2=0.8,ε1=0.2,ε2=0.1.此时基本再生数R0=5.1>1;选定初值S(0)=200,I(0)=120,H(0)=50,R(0)=30.利用Matlab模拟仿真结果如图1所示.从图1可以发现,S,I,H,R的解曲线经过一段时间后全局渐近稳定于地方病平衡点.

图1 地方病平衡点的稳定性
4.2 无病平衡点的全局渐近稳定性
依据假设3,考虑选取函数h(I)=参数设定为A=10,N=400,B=0.001,β=0.003,μ=0.2,γ=0.5,K=200,γ1=0.2,γ2=0.8,ε1=0.2,ε2=0.1,此 时基本再生数R0=0.257 5<1;选定初值S(0)=从图2可以发现,易感染人群S在经过一段时间后到达平衡,已感染的I类人群经过一段时间后逐渐减少,最终趋于消亡的无病平衡状态.

图2 无病平衡点的稳定性
5 结语
经过对右端不连续的非线性出生率和医院容纳的传染病模型的研究,发现所有满足初值条件下的解都会在一个有限的时间范围内趋近于模型的有病与无病平衡点.有限时间的稳定治疗有着其巨大深远的社会现实意义,因为许多病人都希望能够了解到自身的慢性疾病是如何被治疗的,何时被治愈.
利用Matlab数值计算,验证了本文理论推导的正确性.借助Filippov解和微分包含的理论,得出了更加符合实际的动力学模型.由此,可以将右端不连续治疗策略应用于更多领域[9-14].因此通过构建一个更能适应现实规律要求的右端不连续微分方程动力系统,就可以进一步得出更能适应现实规律的结果.
