基于自适应平方根滤波的MHD/MEMS信号融合方法*

蒋 恺，李醒飞，刘 帆，拓卫晓

(天津大学精密测试技术及仪器国家重点实验室，天津 300072)

航天器在轨运行期间，极易受机械振动和空间环境等多种因素的影响，诱发出低幅值、宽频带的微角振动[1-2]。这些微角振动源覆盖频带达千Hz，幅值小，难以测量，处于0.01 μrad到几十μrad量级。随着高精度航天器和机载系统探测距离逐步提升，微角振动成为限制有效载荷指向精度进一步提高的主要因素之一[3]。因此，实现在轨微角振动特征的测量具有巨大意义。

传统陀螺仪的测量精度很高，但工作带宽一般小于20 Hz，微角振动的宽频带测量需求(0.1 kHz～1 kHz)会增加陀螺仪的体积或降低陀螺仪的精度[4]。磁流体动力学(Magnetohydrodynamics，MHD)角速度传感器具有宽频带、低噪声、体积小等优良特性，极其适合测量高频角振动[2]。但MHD角速度传感器存在原理极限，低频时受反电动势和粘滞力的影响较大，输出性能不佳，单独使用时难以满足微角振动测量的需求。

尽管可以通过进一步处理MHD角速度传感器的输出[5]或增加MHD泵等[6]手段改善其非工作频段的测量能力，拓宽测量频带，但要兼顾极宽的测量频带和保持原本的灵敏度仍较困难。为了实现这一目标，国内外诸多学者致力于全频带惯性传感器数据融合技术，来弥补MHD角速度传感器低频测量的盲区。周新力[7]利用混叠滤波器实现了MHD角速度传感器和MEMS陀螺仪的数据融合，实现了0～40 Hz频段内相位波动±1°、幅值波动小于1%的融合效果。Marcelo[8]提出了闭环控制滤波方法，利用高带宽角位移传感器(Angular Displacement Sensor，ADS)和低带宽惯性参考单元(Inertial Reference Unit，IRU)实现了0～100 Hz带宽内姿态角的测量。毛耀[9]提出了闭环控制滤波的最优校正方法，利用MEMS陀螺仪和MEMS加速度计数据融合实现了1 Hz～100 Hz带宽内最大幅值误差2.1 dB，最大相位误差17°的融合效果，有效提升了MEMS陀螺仪的测量带宽。拓卫晓[10]利用闭环控制滤波实现了MEMS陀螺仪和MHD角速度传感器的数据融合，实现了0.1 Hz～60 Hz频带内最大幅值畸变小于0.9 dB，最大相位误差小于34°的融合效果。上述研究均是从能够直观评估融合后数据的相位、幅值以及延迟等特性的频域角度开展的，无法兼顾传感器的漂移和噪声等指标。基于时域的融合方法能够改善传感器融合中的漂移、噪声等指标，在传感器融合领域也得到了学者的广泛关注。Iwata[11]根据应用维纳滤波实现了不同传感器的信号融合，但维纳滤波要求输入信号统计特性已知，且滤波过程中不能自适应调节。金钊、何世民等人[12-13]建立了MHD角速度传感器和星敏感器的卡尔曼滤波框架，并对融合算法进行了仿真验证。纪越[14]对不同频段的数据采用不同的卡尔曼增益计算式，实现MHD角速度传感器和MEMS陀螺仪的融合。相比于MHD角速度传感器，融合输出在低频段的信噪比提升了近10 dB。但该算法需要计算多个卡尔曼增益，并需要识别输入信号的大致范围，采用对应的卡尔曼增益，对于实现算法的MCU提出了较高的要求。韩佳辰[15]应用Allan方差实时计算测量协方差矩阵，实现了MHD角速度传感器和MEMS陀螺仪的自适应融合。相较于MHD角速度传感器，融合后信噪比提高了近10 dB，均方根误差降低了30%。但上述研究均停留在算法和仿真层面，尚未对具体的硬件实现过程进行研究。具体实现时，主控芯片资源有限，部分算法难以实现，有些则因为计算精度的限制，在实际滤波过程中与计算机仿真结果不一致，导致协方差矩阵易失去正定性，导致滤波发散。

针对上述问题，本文基于Joseph形式的协方差更新计算式，提出了一种平方根卡尔曼滤波算法，实现了MHD角速度传感器和MEMS陀螺仪的信号融合。算法在MATLAB平台中通过仿真验证有效性后，移植到FPGA中，并搭配外围电路进行了实验测试，实验结果表明提出的算法在实现MHD角速度传感器与MEMS陀螺仪数据融合方面具有良好结果。

1 传感器复频域模型的建立

1.1 MHD角速度传感器频域模型

MHD角速度传感器表头部分由敏感元件与信号检测电路两部分构成。图1为敏感元件原理示意图，上层圆环为流体通道，内部充满惯性较大的导电流体；下层圆环为永磁体，与传感器外壳固连。当载体发生转动时，导电流体由于惯性作用与惯性空间保持相对静止，从而与永磁体之间产生相对流速，导电流体切割磁感线，在内外壁间产生与输入角速度成正比的动生电动势E。根据非惯性系下的纳维斯托克斯方程，建立如下的传感器敏感元件部分传递函数

图1 MHD角速度传感器工作原理示意图

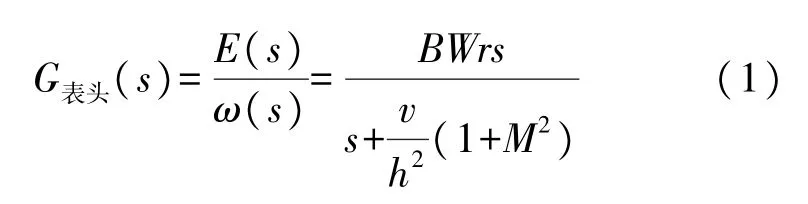
式中:B为磁场强度，ν为导电流体的运动粘度，M为哈特曼数，r为流体环均方根半径，W为流体环宽度，h为流体环的高度。

敏感元件输出的弱电压信号经过调理电路后，作为表头的输出，因此MHD角速度传感器整机的频响特性应为敏感元件部分传递函数与调理电路传递函数的级联。所用的MHD角速度传感器为实验室自研的MHD03型号角速度传感器，带宽为3 Hz～1 000 Hz，复频域模型可表示为

式中:所有系数均为常数。

1.2 MEMS陀螺仪的频域模型

低频性能良好的陀螺仪种类繁多，如光纤陀螺仪、动力调谐陀螺仪等，但大部分都存在体积大的缺陷，难以在安装体积要求较高的场合取得应用。MEMS陀螺仪具有体积小、性能可靠的优点，较为适合用于补偿MHD角速度传感器低频性能。本文选用的MEMS陀螺仪为日本SILICON SENSING公司生产的CRS03型陀螺仪(带宽0～20 Hz)，其复频域模型可表示为

式中:所有系数均为常数。

图2所示为MHD角速度传感器和MEMS陀螺仪复频域模型对应的伯德图，两种传感器的幅度曲线在0～1 000 Hz的频域带内互补，具备实现组合测量的前提。

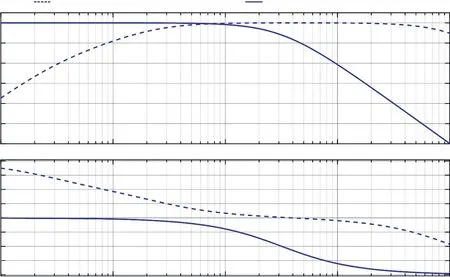
图2 MHD角速度传感器和MEMS陀螺仪伯德图

2 基于Allan方差的平方根滤波算法

2.1 基于Allan方差的卡尔曼滤波模型

实现两个具有不同频带特性传感器融合的卡尔曼滤波模型如图3所示。图中，ωtrue为滤波系统真实输入；ωL，ωH分别为MEMS陀螺仪和MHD角速度传感器的量测值；AL，BL，AH，BH分别为MEMS陀螺仪和MHD角速度传感器的系数矩阵；x1为由滤波系统得到的真实角速度；XL＝[x2x3]T，ηL，νL分别为MEMS陀螺仪的状态变量、系统噪声和测量噪声；XH＝[x4x5x6x7]T，ηH，νH分别为MHD角速度传感器的状态变量、系统噪声和测量噪声。

图3 角速度测量模型

根据图3建立以下自适应卡尔曼滤波方程组。

①状态更新方程

式中:Φk，k-1＝I＋AT，T为所选择的AD的采集周期。

②时间更新方程

估计测量噪声:

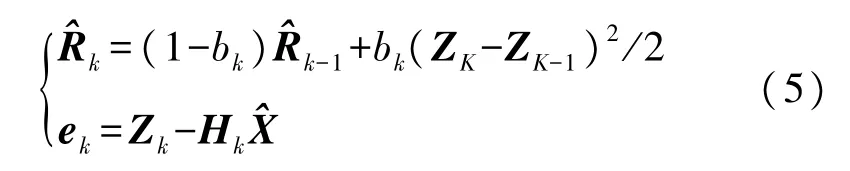
更新状态值和系统过程噪声方差矩阵:

由上式可知，算法在通过测量数据进行滤波递推时，实时估计系统的测量噪声，从而达到自适应滤波的目的。由于整个系统阶数较高，且系数矩阵Φ阵病态，导致协方差矩阵P阵中数据量级相差较大，由于舍入误差的影响，协方差矩阵P阵不再保持原本的正定性，致使滤波发散。

2.2 基于Allan方差的平方根滤波模型的建立

根据矩阵理论，当矩阵正定时，可以分解为两个三角矩阵的乘积，且这两个矩阵互为转置。在卡尔曼滤波中，协方差矩阵P满足该条件，故有

由2.1可知，协方差矩阵P在传递过程中失去正定性，从而导致滤波发散，而利用其平方根Δ进行传递时，则可以保证协方差矩阵的正定性[16]。

基于序贯滤波的平方根滤波流程串行计算较多，难以矩阵化并行实现，结合矩阵平方根的概念和Joseph形式的协方差更新计算式，提出了平方根滤波模型，并利用Allan方差计算式更新量测噪声，实现自适应滤波。具体计算过程如下:

①状态更新方程

式中:第二式表示通过QR分解得到Δk/k-1。

②时间更新方程

测量噪声计算:

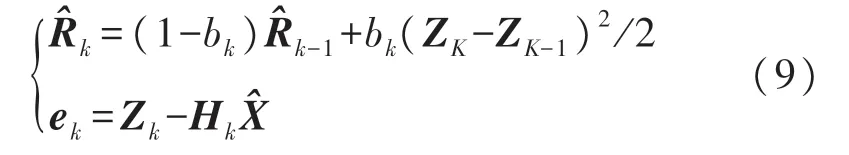
更新状态值和系统过程噪声方差矩阵:

式中:第三式与式(8)中第二式意义相同，表示式子左边的矩阵经过QR分解得到式子右边的矩阵。

经过上述处理，使用协方差矩阵的平方根替代协方差矩阵完成卡尔曼滤波的迭代计算，保证了滤波过程的稳定进行。

3 硬件系统设计与仿真验证

3.1 硬件系统设计

算法需搭配相应的硬件方能正常工作，设计的硬件结构如图4所示，电源系统负责整个电路以及传感器的供电。在传感器输出信号采集之前，由于MHD角速度传感器的标度因数约为MEMS陀螺仪的一半，需要对两种传感器的输出做一定的调理，具体方案为MHD角速度传感器的输出信号进行2倍放大处理，MEMS陀螺仪经过同型号的单倍放大芯片。AD采集后将信号传输至FPGA中，在FPGA将高低频信号融合后传输给上位机，在上位机中通过Labview完成进一步分析。

图4 电路结构设计

图4中供电模块负责满足各个模块的供电需求，根据各模块的需求设计得到电源模块如图5所示。外部输入12 V电源，分为两路，一路经过DC-DC升压并转换后得到±15 V电压，经过LDO降压得到±12 V电压，由于经过LDO降压，此时电源已较为干净，可用于给传感器供电；另一路经过DC-DC降压得到9 V电压，在经过多个型号的LDO降压分别得到5VA、5VB、5VC、5VD等多种5 V电压，5VA和5VB为5 V模拟电压，其对于电源质量要求较高，其中5VB为传感器的供电电源，其输出质量与电源相关，需要采用独立的LDO转换；5VC和5VD为数字电压，5VC为FPGA板供电电源，5VD为采集板供电电源。

图5 电源结构设计

3.2 FPGA逻辑设计

FPGA中执行的逻辑如图6所示，当检测到DRDY端口低电平时，FPGA通过SPI接口接收两路AD同步采集的MHD角速度传感器和MEMS陀螺仪的输出，经过定点转浮点、平方根滤波模块后得到融合输出，将数据转换为定点数后通过约定好的协议进行编码发送，在上位机中进行解码得到融合数据。

图6 FPGA逻辑设计

考虑协方差矩阵更新需要时间较长，因此在将更新好的数据传输出去后再进行计算，以图减小数据在FPGA中暂存时间，从而缩减算法实现造成的相位延迟。

3.3 融合算法的仿真验证

本文基于Modelsim平台对融合算法在FPGA中的执行效果进行仿真验证，选取0.5 Hz、5 Hz、50 Hz三个频率点分别进行验证。仿真得到的融合输出与两个传感器原始数据的对比如图7～图9所示，融合输出在三种频段内都能很好地跟随输入信号。

图7 0.5 Hz处融合效果

图8 5 Hz处融合效果

图9 50 Hz处融合效果

4 实验验证

4.1 实验验证平台

实验验证平台如图10所示，将两个传感器通过工装固连，安装在转台的正中心，通过工装的平面度和垂直度确保两个传感器的敏感轴和转台的旋转轴共线。

图10 融合算法验证实验平台

测试时，控制转台以Ω＝sin(2πft)rad/s的角速度转动，其中f为指定的测试频率。安装在转台上的传感器感应到转台转动，输出与角速度相关的模拟电压值，双通道采集模块采集两路传感器的输出，通过SPI协议将量化的电压值发送给FPGA，在片内对两路传感器数据进行滤波融合，最后将融合数据通过串口输出到上位机，在上位机采用FFT计算该频率下的幅度和相位。

4.2 静态噪声功率谱测试

本文采用经典功率谱评价融合输出的静态噪声。测试静态噪声时，保持转台输入为零。FPGA串口输出端仅可输出一路信号，在测试时控制FPGA依次输出MHD角速度传感器输出、MEMS陀螺仪输出和融合输出，通过上位机的程序进行接收。在MATLAB中利用平均加窗周期法(Pwelch函数)对接收到的数据进行处理，得到输出噪声的功率谱密度曲线如图11所示，融合信号的静态噪声特性与MHD角速度传感器持平。

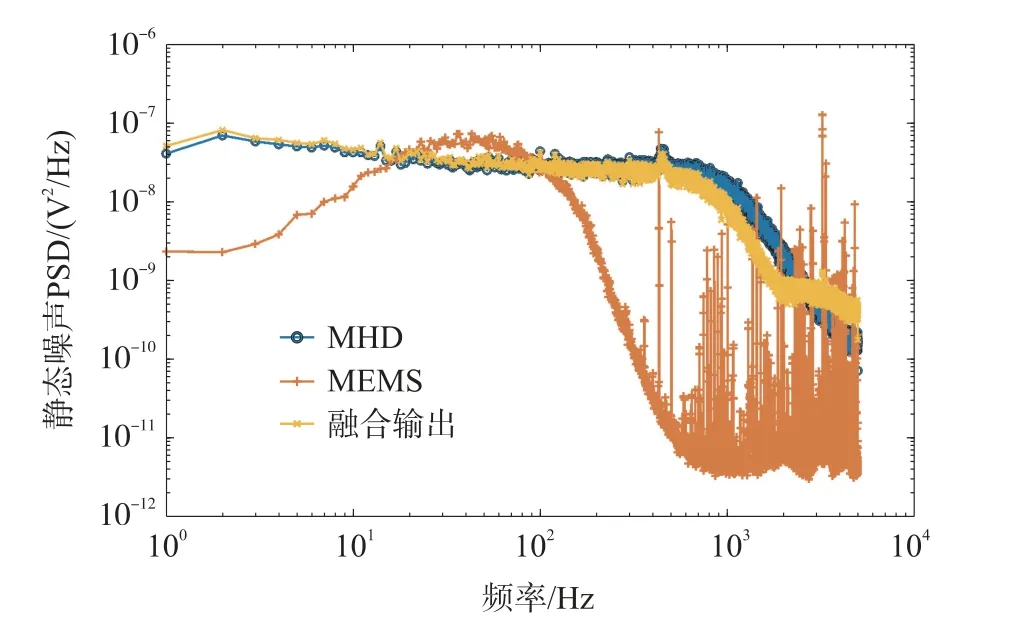
图11 噪声功率谱密度

4.3 标度因数测试

幅频响应特性表征着输出与输入的比值随频率的变化规律，是传感器的重要特性，而标度因数正是这一特性的表现。为测试融合输出标度因数随频率变化的情况，控制转台以稳定幅度、不同频率转动，进行扫频实验。具体的扫频频率选择为0.1 Hz～0.9 Hz内，扫频频率间隔为0.1 Hz；1 Hz～20 Hz内，扫频频率间隔为1 Hz；20 Hz～60 Hz内，扫频频率间隔为5 Hz。分别对输入角速度幅值为20 °/s、30 °/s、40 °/s、50 °/s进行测试，对于不同幅值相同频率点的标度因数取算术平均值，得到的融合输出标度因数如表1所示。

表1 标度因数测试

根据表1可知，在测试的频带内，经过算法融合的标度因数相对于MHD角速度传感器和MEMS陀螺仪的标度因数，明显更为稳定。融合后的标度因数频带内最大波动在2.5%以内，低频段稳定在0.04±0.000 5 V/(°/s)以内，表明算法有效补偿了MHD角速度传感器的低频性能。

4.4 线性度测试

线性度是传感器的重要特性之一，为测试系统标度因数随幅度变化的情况，控制转台以不同幅度、相同频率转动，进行测试实验。1 °/s～50 °/s范围内，幅度间隔为5 °/s。对于每一个频率点都进行以上幅度点的扫幅测试，频率点的选取为0.2 Hz、2 Hz、20 Hz、50 Hz，以上频率点涵盖了低频段、中频段以及高频段，能够较好地评价系统的线性情况。取测量数据与拟合直线之间的最大误差与50 °/s时测量数据的百分比作为评价基准，由于MHD角速度传感器在0.2 Hz处基本感应不到信号，故在0.2 Hz处不对MHD传感器的线性度进行评估，计算得到的其余各频率点线性度如表2所示。从表2可知，融合后的信号保持着MHD角速度传感器优良的线性度，满足测量的需求。

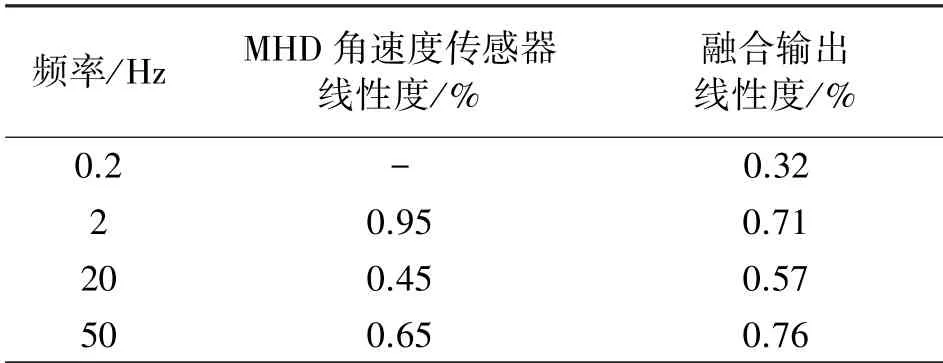
表2 线性度测试

5 结论

MHD角速度传感器具有低噪声、宽频带等优点，但由于反电动势和粘滞力的影响，具有原理极限，难以满足微角振动DC-1 kHz的测量需求。MEMS陀螺仪具有体积小、低频性能良好的优点，在频带上与MHD角速度传感器呈互补特性。本文基于Joseph形式的卡尔曼滤波，提出了一种平方根滤波算法，利用Allan方差实时更新测量协方差矩阵，实现了MHD角速度传感器和MEMS陀螺仪数据的实时融合。线性度和静态噪声测试结果表明融合输出的噪声水平和线性度与MHD角速度传感器相当。扫频实验结果表明算法能够有效补偿MHD角速度传感器的低频测量盲区。