新月形覆冰输电导线脱冰跳跃高度风载放大系数研究

2022-11-21楼文娟张跃龙黄铭枫

振动与冲击 2022年21期

楼文娟，张跃龙，黄铭枫

(浙江大学结构工程研究所，杭州 310058)

输电导线脱冰产生的严重竖向振动，可能会导致导线及导地线间的间隙小于电气绝缘间隙，从而引起线路闪络跳闸等事故发生，危及电力传输。一般认为，导线脱冰跳跃高度主要取决于脱冰产生的冲击作用，而实际上也可能受到风载的耦合影响，因为导线脱冰前后存在显著的气动力突变。为了设计合理的输电线路电气绝缘间隙，需要考虑风载和脱冰对导线跳跃高度的耦合作用。

目前，国内外学者基于无风假设下已经开展了大量输电导线脱冰跳跃动力响应有关研究[1-10]。Gong等采用非线性有限元方法研究了高差对导线脱冰跳跃高度的影响，给出了跳跃高度与导线脱冰前后静止状态弧垂差的函数关系。Huang等基于动力相似关系设计了三跨输电线路的缩尺模型，借助该模型研究了不同分裂数、跨距、高差、导线初始应力、覆冰厚度和脱冰率下输电线路脱冰动力响应。可以看出，以往大多数研究仅考虑了脱冰冲击带来的影响，然而风载作用对导线脱冰跳跃高度的耦合影响还有待进一步研究。刘敏等[11]通过开展三跨输电导线缩尺模型试验，研究了脱冰量、脱冰位置、冰厚和风速等参数变化对导线脱冰跳跃动力响应的影响，发现风载作用会抑制脱冰跳跃高度而加剧张力和轴力响应。姚陈果等[12]仿真分析了导线10 mm均匀覆冰时，不同风速下导线脱冰动力响应，研究结果表明随着风速的增大导线跳跃高度和最大动张力均略有减小。上述研究忽略了覆冰导线真实冰形对气动力特性的影响，未能精细化考虑风载作用。

本文研究了新月形覆冰输电导线脱冰跳跃高度风载放大系数η，来考虑风载对脱冰跳跃高度的耦合影响，并探讨了风速、覆冰厚度、风攻角及脱冰率等参数对系数η的影响。通过开展高频天平测力风洞试验获得了不同厚度新月形覆冰导线的气动力系数，从而精细化考虑了风载取值。最后基于最小二乘法给出了风载放大系数η的拟合公式，可供设计使用。

1 新月形覆冰导线气动力特性风洞试验

本文以某500 kV四跨四分裂高压输电线路为原型，开展了典型新月形覆冰导线气动力特性风洞试验。子导线型号为LGJ-400/35，外径D为26.82 mm。4种新月形覆冰导线刚性模型采用ABS(acrylonitrile butadiene styrene)材料按1∶1制作而成，其模拟覆冰厚度分别为0.25D，0.50D，0.75D，1.00D，刚性模型横截面，如图1所示。

(a)

(b)

(c)

(d)图1 新月形覆冰导线模型横截面Fig.1 Cross section of crescent-shaped iced conductor models

刚性模型高频天平测力风洞试验在浙江大学ZD-1边界层风洞中开展,如图2所示，流场设置为5%均匀湍流。试验中风攻角范围为0°～180°，间隔5°，气动力及风攻角定义，如图3所示。试验获得的4种冰厚下新月形覆冰导线的升力、阻力系数如图4所示[13]。

图2 风洞试验照片Fig.2 Photo of wind tunnel test

图3 气动力和风攻角α定义Fig.3 Definition of aerodynamic force and wind attack angle α

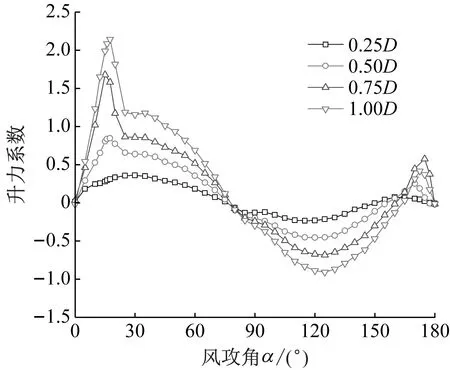
(a) 升力系数

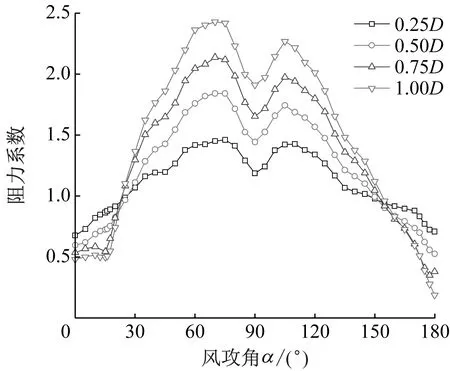
(b) 阻力系数图4 新月形覆冰四分裂导线气动力系数Fig.4 Aerodynamic coefficients of crescent-shaped iced four-bundled conductors

2 基于有限元法的导线脱冰跳跃高度研究

2.1 线路概况

考虑到输电塔对导线脱冰跳跃高度的影响可以忽略[14]，本文以浙江某500 kV高压输电线路为原型，在ANSYS软件中建立了导线-绝缘子耦合的有限元模型，模拟了冰风耦合作用下导线跳跃高度。线路的几何参数，如图5所示；导线和绝缘子参数分别如表1、表2所示。图5中:h为导线挂点高度;L为跨距，悬垂绝缘子串编号分别为1～3。表1中，S,E,ρstr,F0和μ分别为导线有效截面积、弹性模量、线密度、初始张力、泊松比。表2中，Lj和Mj分别为绝缘子的长度、质量。

图5 输电线路几何参数Fig.5 Geometric parameters of the transmission line

表1 LGJ-400/35导线物理参数Tab.1 Parameters of LGJ-400/35 conductor

表2 绝缘子物理参数Tab.2 Parameters of insulator

2.2 冰风耦合仿真计算方法

由于线路所处位置为B类地貌，采用指数律可以获得导线各节点处的平均风速[15]。采用Kaimal谱[16]并结合Davenport空间相关性[17]，基于谐波叠加法可以生成各节点处的脉动风速。截取频率的上下限分别取2π,0；为保留脉动风时程中的低频部分，频率采样点数取2 048；脉动风模拟时长为2 048 s；为消除脉动风模拟过程中可能出现的混叠和失真，时间步定为65 536，相应的时间间隔为1/32 s。为研究风速对导线脱冰跳跃高度的影响，本文模拟生成了10 m高度处0～20 m/s(间隔5 m/s)的风速。本文通过在有限元模型节点位置处施加集中荷载来模拟导线覆冰，冰形为新月形且对应的冰厚δ分别取0.25D,0.50D,0.75D和1.00D，覆冰密度取900 kg/m3，通过在极短时间内移除冰载来模拟脱冰过程产生的冲击作用。

在风载和脱冰冲击的耦合作用下，输电导线的运动方程可以表示为[18]

K2N×2N[YZ]T=[FYFZ]T

(1)

Y=[Y1,Y2,…,YN]T

(2)

Z=[Z1,Z2,…,ZN]T

(3)

(4)

输电线路是对风载敏感的非线性结构[19]，流固耦合作用下会产生显著的气动阻尼，尤其是在大风作用下[20-21]。为考虑气动阻尼作用，在计算覆冰导线上作用的风载时，应考虑导线与来流的相对速度。导线离散质点模型中，第i个节段与来流的相对速度，如图6所示。图7给出了第i个导线节段受到的气动升力FLi和阻力FDi。在图6、图7中，βi为来流速度Ui和相对速度Uri之间的夹角。气动升力FLi和阻力FDi可表示为

(a)

(b)图6 导线与来流的相对运动Fig.6 Relative movement of a conductor to the incoming flow

图7 导线节段i受到的气动力Fig.7 Aerodynamic forces on the conductor segment i

(5)

其中

(6)

(7)

将导线节段受到的气动阻力、升力分别向水平和竖直方向投影，可以得到水平风荷载FYi和竖向风荷载FZi

(8)

考虑导线与来流相对速度时，式(1)中的FY,FZ可以表示为

(9)

(10)

(11)

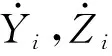
采用瑞利阻尼模型来考虑导线的结构阻尼[22]，表达式如下

Cstr=αM+βK

(12)

其中常系数α和β为

(13)

式中：ξ为结构阻尼比，取0.5%；ω1和ω2分别为导线前两阶自振频率。

对于多跨输电线路来说，中间跨的脱冰往往产生最不利的动力响应[23]，因此脱冰模式选定为最长的第三跨脱冰，脱冰率β分别取50%,80%和100%。对图8中输电线路在冰风耦合作用下的跳跃高度进行时域分析，仿真计算中采用无条件稳定的Newmark方法对非线性方程式(1)直接积分求解。

(a) 整体模型

(b) 局部放大模型图8 有限元模型和脱冰模式Fig.8 Finite element model and ice shedding mode

2.3 仿真计算结果分析

风荷载对输电导线脱冰跳跃高度的影响与风速U、覆冰厚度δ、风攻角α及脱冰率β密切相关。本文10 m高度处的U取0～20 m/s，间隔5 m/s；δ取0.25D,0.50D,0.75D和1.00D；α取0°～180°，间隔10°；β取50%,80%和100%；共计340个数值计算案列。

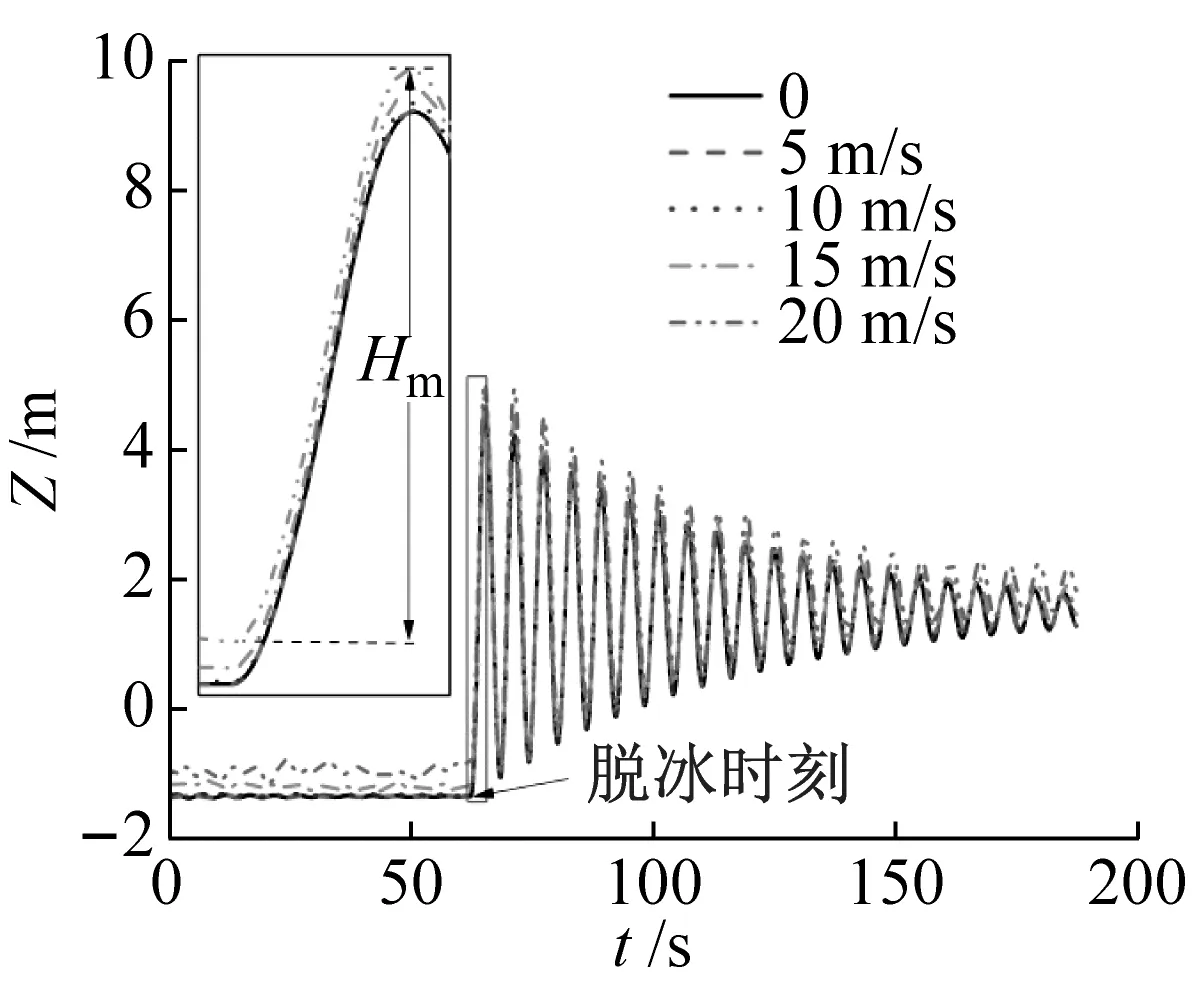
仿真计算了风攻角0°,70°和130°下，导线脱冰竖向位移Z，如图9所示。其中，覆冰厚度和脱冰率分别取1.0D,100%。可以看出，风载对导线脱冰跳跃高度Hm的影响与风攻角α密切相关；在130°风攻角下，风载的作用会明显增大导线脱冰跳跃高度Hm，因为此时导线受到升力的方向与冰载方向一致，脱冰后升力的骤减会加剧导线脱冰冲击。在70°风攻角下，风载会明显抑制导线脱冰跳跃，这与该攻角下的特殊气动力特性有关，即气动阻力大而升力小；在0°风攻角下，风载的作用对Hm的影响很小。

(a) α=0°

(b) α=70°

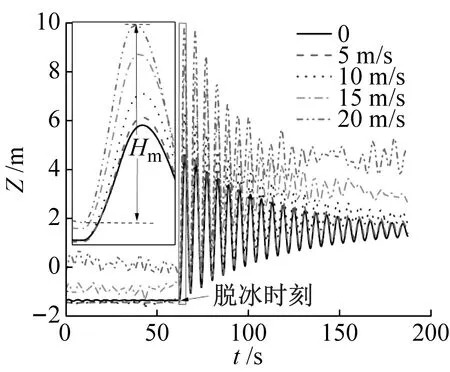
(c) α=130°图9 不同风速下导线脱冰竖向位移(δ=1.00D， β=100%)Fig.9 Vertical displacement of conductor following ice shedding under different wind speeds(δ=1.00D， β=100%)

3 脱冰跳跃高度风载放大系数参数化研究

图9的仿真计算结果表明，在确定合理的线路设计绝缘间隙时，需要考虑风载的作用。因此，本文定义脱冰跳跃高度风载放大系数η来表征风对导线脱冰跳跃高度的影响，它是与风速U、覆冰厚度δ、风攻角α及脱冰率β相关的函数

(14)

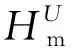
3.1 风攻角敏感性分析

对于不同冰厚δ的新月形四分裂导线，分析了当风速U为10 m/s、脱冰率β为100%时，不同风攻角α下的脱冰跳跃高度风载放大系数η,如图10所示。可以看出，放大系数η对风攻角的变化很敏感，随着风攻角的变化呈近似的正弦状非线性变化。η的最大值和最小值分别出现在130°和20°风攻角处，因为在这两个风攻角下，导线分别受到最大的负升力和正升力(升力向上为正)，会分别加剧、减少脱冰冲击。当风攻角范围在100°～150°时，η>1，说明风的作用会明显增大导线脱冰跳跃高度，忽略风载的影响会导致输电线路电气间隙设计偏不安全；而对于其他攻角，η≤1，说明此时风载的影响不明显，甚至会抑制导线脱冰跳跃。

图10 不同风攻角下的η(U=10 m/s， β=100%)Fig.10 η under different wind attack angles (U=10 m/s， β=100%)

在100°～150°风攻角下，覆冰厚度的增加会导致系数η的显著非线性增加，这是因为覆冰导线的气动力特性对其脱冰跳跃高度有重要影响，冰厚增加引起的气动升力增加，导致风对导线脱冰跳跃高度的加剧效果更显著。

3.2 风速敏感性分析

针对4个典型风攻角0°，70°，130°和180°，研究了不同风速U和冰厚δ下的放大系数η，相应的结果如图11所示。在数值模拟过程中，脱冰率β设定为100%。可以看出，风载放大系数η对风速和冰厚的变化均敏感，在5 m/s以内的低风速情况下，4个典型风攻角下的η取值均接近1.0，表明风的作用对导线脱冰跳跃运动没有明显的贡献。在130°和180°风攻角下，η随风速的增大而增大；而在0°和70°风攻角下，η随风速的增大而明显减小，这表明，只有在具有明显负升力的风攻角下，风速的增加才会对促进跳跃高度起到积极作用。

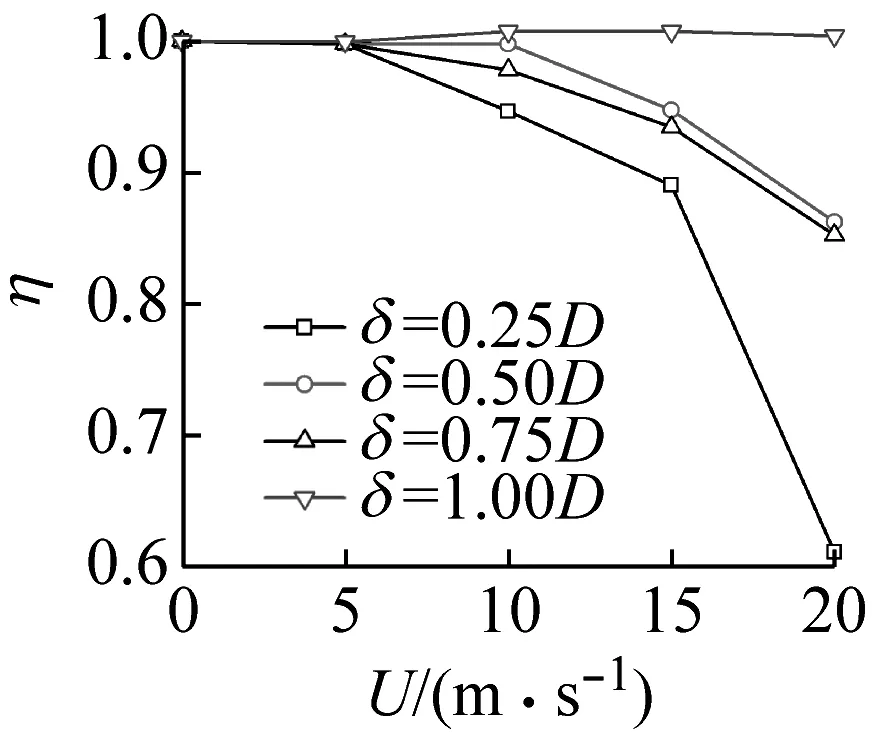
(a) α=0°

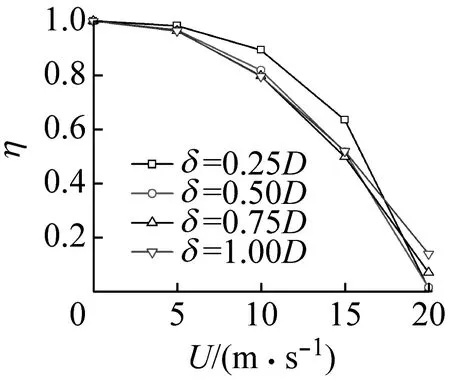
(b) α=70°

(d) α=180°图11 不同风速和冰厚下的η(β=100%)Fig.11 η under different wind speeds and ice thicknesses(β=100%)

在5 m/s以内的低风速情况下，冰厚的增加对η的影响较小。而随着风速的增加，η对覆冰厚度的变化显得更加敏感。

3.3 脱冰率敏感性分析

图12用η(β1)/η(β)比值来说明η系数对脱冰率的敏感性。η(β1)和η(β)分别表示不同脱冰率β1,β下η的取值，此时η的其他变量δ,U和α保持一致。可以看出，在不同的数值计算工况下，η的比值均接近于1.0，说明系数η受脱冰率变化的影响较小。

图12 不同脱冰率下η的比值Fig.12 Ratio of η under varied ice shedding rate

3.4 风载放大系数η拟合公式

由于导线脱冰跳跃高度风载放大系数η与风攻角α密切相关，因此本文着重研究了在危险风攻角下(即100°～150°)的系数η，此时风的作用会明显加剧导线脱冰跳跃高度(η>1)。对于其他风攻角，风对导线脱冰跳跃的影响不明显甚至有抑制作用(η≤1)，因此可以保守地取η为1.0。考虑到系数η(δ,U,α,β)对脱冰率的变化不敏感，可以将其描述为给定风攻角下，关于风速和冰厚的函数。通过非线性有限元方法计算了风攻角在100°～150°时，新月形覆冰导线在0～20 m/s风速和0.25D～1.00D冰厚下的系数η。并对这些数据进行了最小二乘拟合，拟合结果如图13所示，得到了η的计算公式

图13 式(15)和数值模拟得到的η对比(δ=1.00D)Fig.13 Comparison of η calculated by Eq.(15) and numerical simulation (δ=1.00D)

η=

(15)

式中，δ为新月形覆冰基于面积等效成圆形覆冰后的厚度。在设计中，当η<1时,应保守的取η=1.0。从图13可以看出，式(15)可以较为准确的计算脱冰跳跃高度风载放大系数η。值得注意的是，式(15)是基于新月形覆冰导线得到的，而不同覆冰形状的输电导线由于其气动力特性存在差异，式(15)可能不适合，但可以采用本文类似的方法得到其他冰形下的系数η。