原始对偶内点法下的圆柱度误差评价技术研究
2022-11-21姜菲菲赵凤霞牛森涛
姜菲菲,赵凤霞,牛森涛,郑 鹏
(郑州大学机械与动力工程学院,河南 郑州 450001)
1 引言
回转体零件的形状误差对机械产品的寿命、工作精度等都有很大的影响,对于一些精密仪器和在恶劣条件下工作的机器影响可能更甚,因此常常需要控制回转体零件工作表面的形状误差。圆柱度误差是实际圆柱面对基准圆柱面的变动量,它既包含轴剖面方向的误差,也包含横剖面方向的误差,是圆柱体各项形状误差的综合指标。因此,圆柱度是回转体零件的最典型技术指标。
目前国内外学者围绕圆柱度误差的评定进行了很多研究。文献[1]提出了一种基于遗传算法的圆柱度误差评定方法;文献[2-3]等分别采用基于修正单纯形法和基于运动几何学的最小区域优化算法对圆柱度误差进行了评定;文献[4]提出应用粒子群优化算法进行圆柱度误差的评定;文献[5]应用包含收敛因子的粒子群优化算法进行圆柱度误差的评定;文献[6]提出了一种基于网格搜索算法的圆柱度误差评定方法;文献[7]采用序列二次规划算法思想对圆柱度误差进行计算;文献[8]提出了一种基于拟粒子群算法的圆柱度误差评定方法,由拟随机序列生成粒子群的初始位置与初始速度;文献[9]采用改进差分进化算法实现了圆柱度误差的评定;文献[10]提出了一种基于改进的粒子群优化算法的圆柱度误差评价方法,粒子群采用贪心选择法来选择最佳候选解;文献[11]采用双圆心拟合与端面网格搜索算法对圆柱度误差进行计算。综上可知,国内外学者一直在寻求一种评定精度高、运算速度快、评定结果重复性好的圆柱度误差评定算法。
1984 年,Karmarkar 开创性地提出将内点法推广应用到对线性规划的求解中,原始对偶内点法是由内点法发展而来的一种算法。原始对偶内点法相比于其他算法,它是一种多项式的时间复杂性算法,极大地提高了线性规划问题的求解速度[12-13]。而且原始对偶内点法是一种在可行域的内部寻优的方法,约束条件和变量数目的增加不会导致迭代次数的增加,因此原始对偶内点法对于较大规模的线性规划问题很友好,可极大地提高其求解速度[13-14]。这里提出应用原始对偶内点法进行圆柱度误差的评定,并对其评定精度、运算效率和重复性进行了实验验证。
2 圆柱度误差评定模型
圆柱度误差是指实际圆柱面对基准圆柱面的变动量;按照ISO 121180-1[15],基准圆柱面有最小二乘基圆柱面、最小区域基圆柱面、最小外接基圆柱面和最大内切基圆柱面,其中,最小区域基圆柱面是用于仲裁圆柱度误差合格与否的基准面,因此这里主要研究基准圆柱面为最小区域基圆柱面时的圆柱度误差评定方法。
如图1 所示,设圆柱面上各测点的坐标为Pi(ri,θi,zi) (i=1,...,N),其中,N为测点总数。假设被测圆柱面的轴线在z=0的平面内相对于基圆柱轴线的偏移量为(x,y),且沿原方向与原轴线分别倾斜α,β,则被测圆柱面上的点到基圆柱面轴线的距离为:

图1 圆柱度误差评定模型示意图Fig.1 Model of Minimum Zone Cylindricity Error Evaluation

展开式(1),可得到:
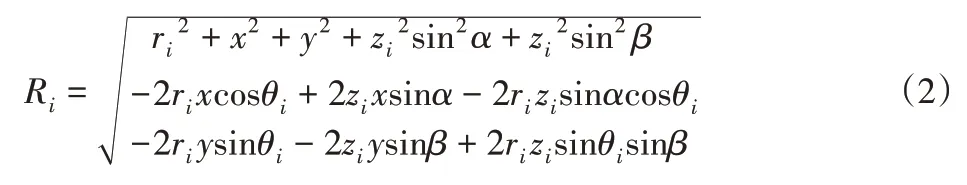
基圆柱体轴线的偏移量相较于圆柱体的名义尺寸而言可以认为是微量,即x,y,α,β均为微量,由“小偏差”理论可知:sinα≈α,sinβ≈β,x,y,α,β任意组合的乘积项可近似视为0,则式(2)可近似为式(3)。

对式(4)配方,可得到:
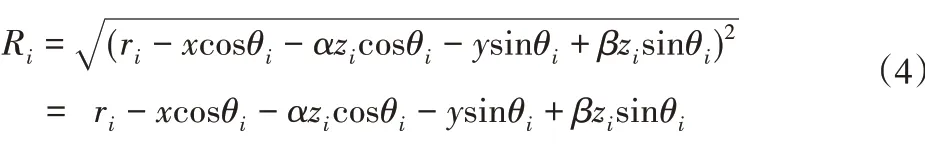
由最小区域圆柱度误差的定义可知,圆柱度误差为:

设u=max(Ri),v=min(Ri),则最小区域圆柱度误差求解模型为:
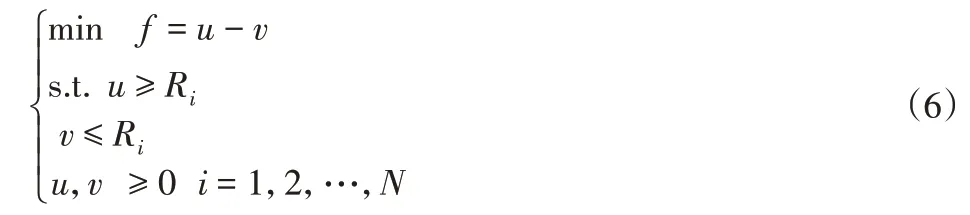
式(6)中的圆柱度误差评定模型是略去了高次项后得到的线性模型,推导可知该模型的误差近似为:

式中:R—圆柱公称半径;d—{|x|,|y|,|αzi|,|βzi|}中最大的值。
3 原始对偶内点法的基本原理
由式(6)可知,所建立的最小区域圆柱度误差评定模型是一个线性规划模型,可采用原始对偶内点法(Primal-dual interiorpoint algorithm)进行计算。
原始对偶内点法的基本思想是结合原问题和对偶问题,利用对偶间隙将不等式约束问题转化为等式约束问题,在可行域内部搜索找到对偶间隙为零的可行解。
对标准的线性规划问题P:

其对偶问题Q为:

式中:s—松弛变量。
引入对数障碍函数,问题D可转换为式(10)。

式中:s=diag(s1,s2,...,sn),μ—障碍参数(μ>0)。
则其相应的Lagrange函数为:

式(11)的最优条件是要满足对x,y,s的一阶导数为0,即可得到式(12)。
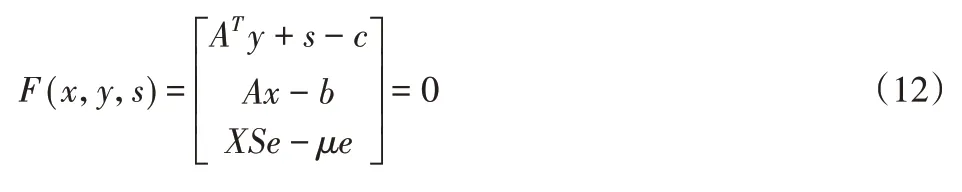
问题即可转化为对非线性方程组式(12)的求解,可利用牛顿法对之求解。
设其初始值为(x0,y0,s0),搜索方向为(Δx,Δy,Δs),可得到如下的方程组。
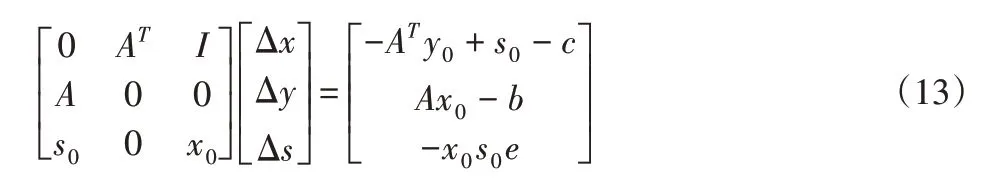
对式(13)求解,可得到(Δx,Δy,Δs),则:

一直迭代,直到在可行域内找到满足一定精度ε的最优解。原始对偶内点法的流程,如图2所示。
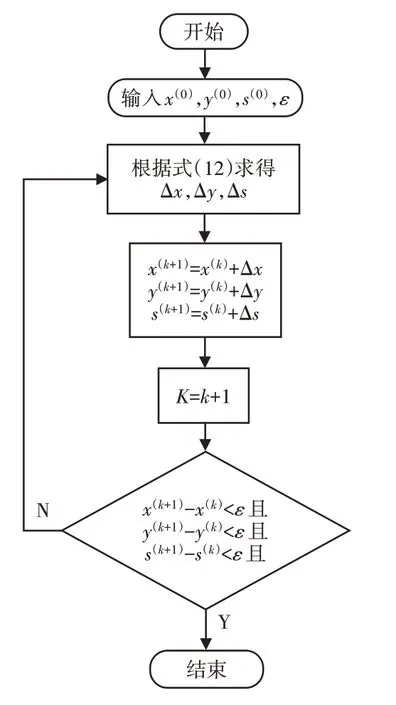
图2 原始对偶内点算法流程图Fig.2 Flowchart of Primal-Dual Interior Point Algorithm
4 实验分析
4.1 文献数据测试
为了测试这里所提出的原始对偶内点法(简称内点法)的有效性,使用参考文献[2,4]中的测量数据按这里所建立的模型和提出的算法进行实验,精度ε设置为1E-7。实验结果,如表1、表2所示。所用计算机CPU i5-6200U,8G内存。从表中可以看出,这里所提出的原始对偶内点法评定精度优于单纯形法和含收敛因子的PSO,且评定时间仅需20ms,评定效率高。

表1 文献[2]数据评定结果Tab.1 Evaluation Results of Reference 2 Data

表2 文献[4]数据评定结果Tab.2 Evaluation Results of Reference 4 Data
4.2 实测数据
实验数据采用海克斯康三坐标测量机(CMM)测量某圆柱体所得的测量数据(5个截面,每个截面1024个测量点),部分数据,如表3所示。采用内点法对圆柱度误差进行评定,实验测试10次结果,如图3、表4所示。可以看出,基于原始对偶内点法的评定重复性好。
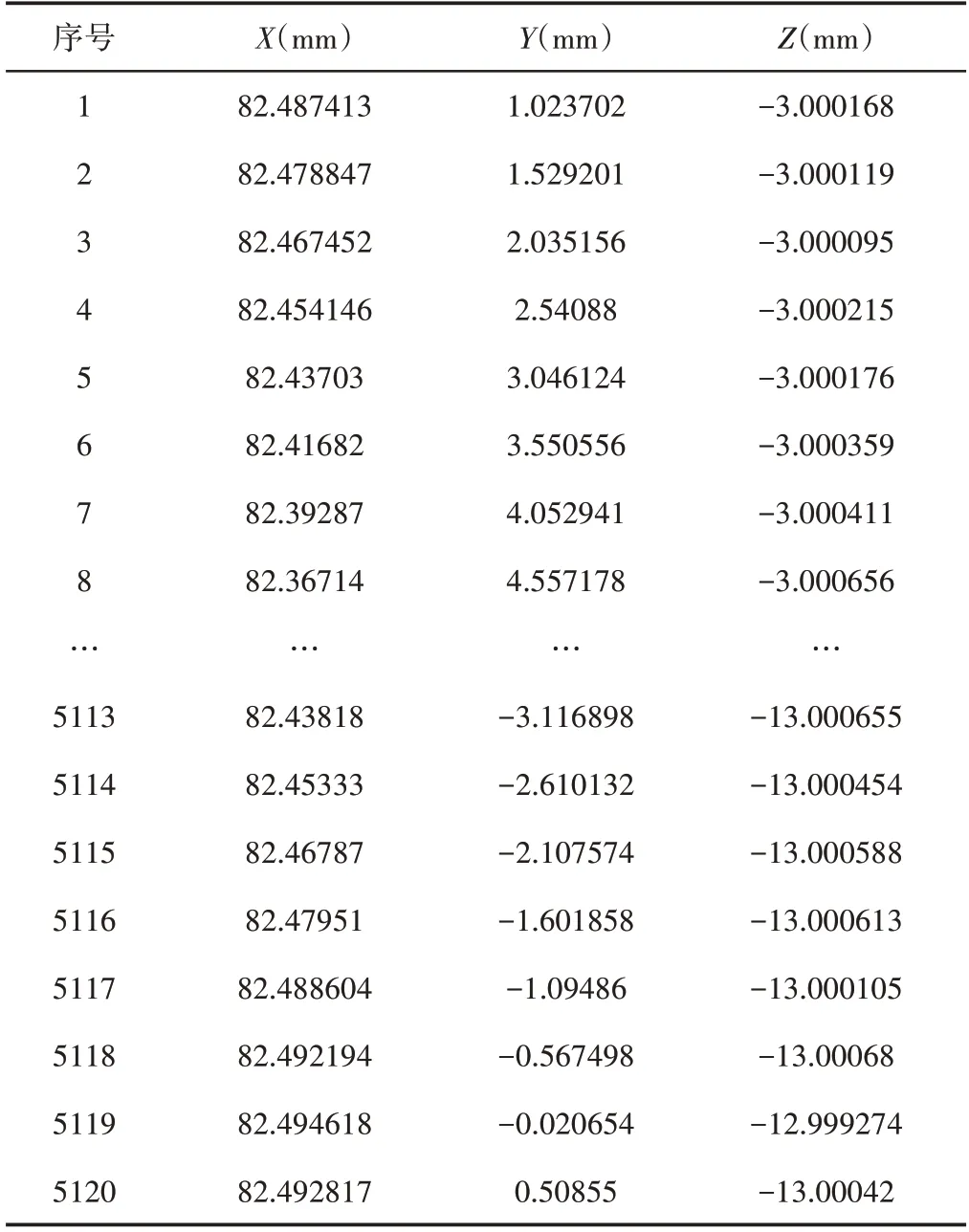
表3 测量数据Tab.3 Measurement Data

表4 实测数据评定结果Tab.4 Evaluation Results of Table 3 Data

图3 实测数据评定结果重复性测试图Fig.3 Repeatability of Measured Data Evaluation Results
4 结论
这里基于“小偏差”假设建立了最小区域圆柱度误差评定模型,根据所建立的评定模型特点,提出采用原始对偶内点法对所建立的圆柱度误差模型求解。采用文献数据和实测数据分别进行了实验验证,结果表明这里所提出的原始对偶内点法在评定精度、评定效率和评定结果重复性等方面均优于现在常用的一些算法。该研究为实现圆柱度误差的数字化计量提供了一种稳定可靠的方法。
