力矩促动器的迟滞非线性建模校正

刘攀登，杜福嘉，宫雪非

（1.中国科学院国家天文台南京天文光学技术研究所，江苏 南京 210042；2.中国科学院天文光学技术重点实验室（南京天文光学技术研究所），江苏 南京 210042；2.中国科学院大学，北京 100049）

1 引言

随着天文观测需求的发展，天文学家对望远镜成像质量的要求越来越高。为了保证成像质量，需要通过改变镜面的面形来校正像差。Nelson基于弹性变形理论提出力矩促动器技术，通过力矩作用使镜面产生弯曲变形，对校正离焦、像散等像差具有明显作用［1］，相比较于传统的力促动器，力矩促动器主要用来校正低频误差，且不承担载荷。

因此，力矩促动器技术日益成为国际上大望远镜镜室制造的关键技术［2］，国外的三十米级大望远镜TMT 和E-ELT 均采用了力矩促动器技术。研究高精度的镜面力矩促动器控制系统，对于未来我国建设10m级甚至更大口径的望远镜有极为重要的意义［3-4］。

在工程实践中，通常使用应变片来检测力矩传感器的输出力矩，然而，由于弹簧叶片材料（航空铝）本身力与应变之间存在的迟滞非线性特性，导致通过应变来检测力矩促动器输出力存在较大误差，这严重限制了力矩促动器的控制精度。

针对迟滞非线性问题，国内外学者在压电陶瓷和磁滞伸缩领域对迟滞特性进行了深入研究［5-6］，目前研究人员主要是通过建立迟滞模型来校正迟滞非线性［7］，目前已有的迟滞模型，根据建立模型的原理不同，可以分为原理迟滞模型和现象迟滞模型［8］，原理迟滞模型是对迟滞产生的机理进行物理求解［9］，求解出输入输出的物理方程从而建立迟滞模型，但是建模困难，且模型适用性范围较差。而基于现象的迟滞模型主要是通过对实际数据进行拟合，简单可靠，具有代表性数学模型比如由文献［10］提出的Perisach模型，文献［11］使用改进的Preisach模型将压电陶瓷的位移误差降低到0.14μm，但是此模型参数较多，计算复杂。此外，由文献［12］提出的Prandtl-Ishilinskii（PI）模型相比较于Perisach 模型，结构较为简单，参数少，易于辨识，并且存在解析逆，广泛应用于压电陶瓷的迟滞补偿［13-15］，文献［16］就采用了PI模型对压电变形镜的迟滞特性就行了校正，使开环精度提高了70%。虽然力矩促动器与压电陶瓷致动器采用的材料和迟滞原理不同，但对迟滞问题的补偿方法基本相同。因此这里采用PI模型对力矩促动器的迟滞非线性进行校正。首先建立力矩促动器应变-力控制系统的迟滞模型并优化算子个数，然后利用迟滞逆模型求出消除迟滞后的补偿电压，对补偿电压进行闭环控制，实现电机输出轴上力的高精度线性控制。

2 力矩促动器工作原理及迟滞特性

力矩促动器工作原理示意图，如图1所示。步进电机固定在下层的基座上，电机输出轴与弹簧叶片连接在一起，弹簧叶片另一端连接Whiffletree三脚架，Whiffletree三脚架与基座通过柔性铰链连接在一起，当电机输出位移顶起弹簧叶片后，会在弹簧叶片另一端产生一个力矩，从而改变了Whiffletree三脚架上的力的分布，使镜面面型发生改变，实现对低阶像差的校正。

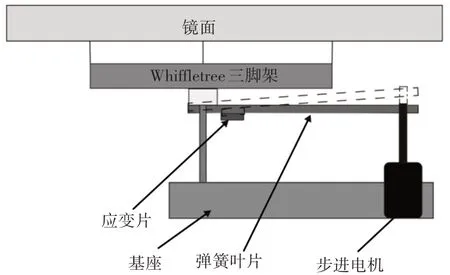
图1 力矩促动器工作原理Fig.1 Working Principle of Warping Harness

为了实际安装使用方便，降低机械结构设计的复杂性，使用应变片测量电机输出轴上的实际输出力。在保证校正低阶像差的前提下，使用应变片测量电机输出力的精度应该控制在0.5N之内。经过对弹簧叶片进行静力学分析，如图2 所示。弹簧叶片在受力发生形变时，弹簧叶片根部与Whiffletree 三脚架连接处的位置产生的应变最大，因此，将应变片粘贴在此处，测量分辨率最高。为了实现通过应变来精确测量三条Whiffletree支撑轴上力，应变电压与电机输出轴上的力应该成线性关系。但是，实验测量数据，如图3所示。电机输出轴上的力在增大和减小的过程中会产生不同的应变，即应变-力测量系统存在迟滞性。如果想实现电机输出力的精确测量，需要对这个迟滞特性进行校正，以达到期望的控制精度。

图2 弹簧叶片的静力学分析Fig.2 Static Analysis of Leaf-Spring

图3 力矩促动器迟滞曲线Fig.3 Hysteresis Characteristics of Warping Harness

3 PI迟滞模型

3.1 PI迟滞建模

PI模型的参数一般包括阈值ri、权值向量wi。每一组参数都构成一个简单的滞回系统，也叫play算子，PI模型是由多个play算子加权叠加构成，单个play算子的表达式为：

初值条件为：

将n个play算子乘以权值wi后进行叠加即可得到力矩促动器的迟滞PI模型，表达式为：

式中：n—算子个数；

u(t)—t时刻的电压输入；

f(t)—t时刻的建模输出；

wi—第i个算子的权值；

ri—第i个算子的阈值。

其中，play算子的阈值ri=i=1，2，…，n。rmax应当小于输入电压的最大值，具体取值应当为保证PI模型存在解析逆时的最大值。

权值wi的取值是通过最小二乘法找出最优解，然后对力矩促动器的迟滞曲线进行参数辨识得到的。

将PI模型表达式（3）写为向量形式：

力矩促动器在?t时刻的实际测量数据中的输出力为y(t)，则t时刻建模误差e(t)为：

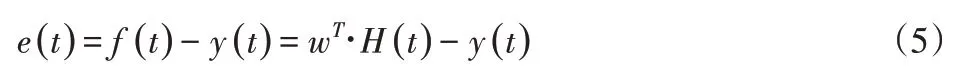
根据最小二乘法，误差函数的平方和取最小值时，wT由最优解，由式（6）可知，误差的平方和有最小值，因此这就是要找的最优解。

由于力矩促动器迟滞曲线中上升和下降过程的不对称性，不能共用一套模型参数，因此需要对上升和下降过程分别进行辨识，根据上述式（3）、式（6），结合测量得到的如图3所示的电压-力迟滞曲线，基于PI模型进行参数辨识，分别求出上升和下降过程的权向量wT、阈值r，然后代入式（3），也就是PI模型的表达式，即可得出力-应变系统的PI迟滞模型。

从式（3）可以看出，辨识出的PI模型的准确度与算子的个数有关。根据最小方均根算法（Least Mean Square）算法，通过使用不同数目的算子进行建模，然后计算模型误差的均方根，可以找出最优的算子个数。算子数目不同时辨识出的PI模型与实际数据的误差方均根，如图4所示。当算子增加到25个以后，PI模型的辨识误差基本趋于稳定。同时，随着算子个数的增加，控制系统计算补偿电压的运算量也会随之增加，系统迟滞补偿的速度也会相应变慢，不利于实验进行实时的补偿校正。

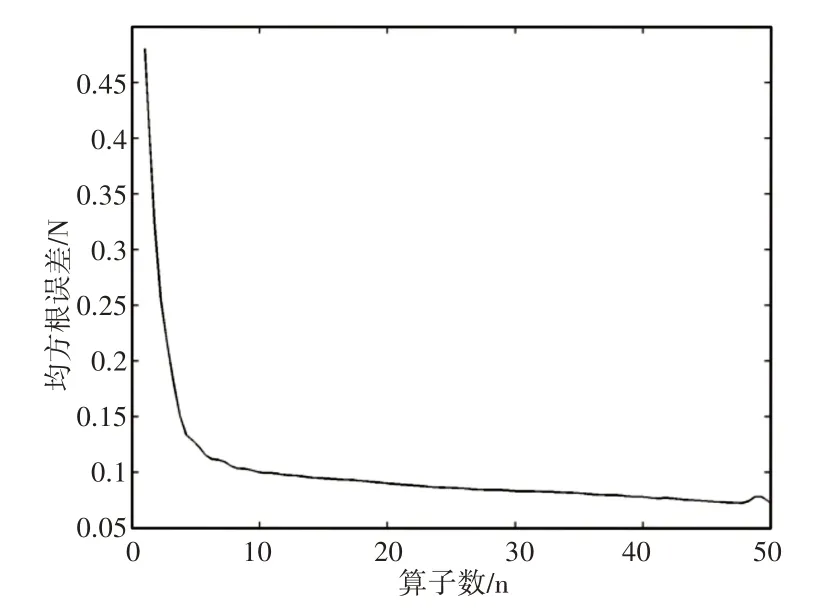
图4 辨识误差下降曲线Fig.4 Error Decline Curve

因此，为了兼顾系统的迟滞模型的误差和系统的运算时间，实验最终选择25个算子来进行PI模型辨识，辨识结果，如图5所示。模型辨识误差，如图6所示。此时PI模型的建模结果与实验数据基本一致，误差也控制在很小的范围内，误差的方均根值（Root Mean Square）为0.0811N。因此，当我们选择25 个算子进行建模时，可以满足补偿控制的需求。

图5 力矩促动器迟滞建模结果Fig.5 Modeling Results of Warping Harness Hysteresis

图6 PI模型建模误差Fig.6 Modeling Error

3.2 PI逆模型

由于PI模型存在解析逆，所以可以通过PI逆模型与PI模型之间互逆的关系计算出PI逆模型的阈值向量和权系数向量，其向量元素分别为：

PI逆模型算子的初始值为

同理，PI逆模型在t时刻的输出表达式为：

将3.1中计算出的上升和下降过程的PI迟滞模型参数分别代入式（7）～式（9），即可计算出各自的逆模型的参数；然后将逆模型参数代入逆模型的输出表达式（10），即可分别求出力矩促动器上升和下降过程迟滞补偿的PI逆模型。

使用PI逆模型补偿的原理，如图7所示。首先测量得到力矩促动器控制系统的实际迟滞曲线，然后进行模型辨识，分别得到上升过程的PI逆模型和下降过程的PI逆模型。然后根据力矩促动器校正面形时的输入的期望力f（t），与上一时刻的期望力f（t-1）进行比较，确定此次校正是上升过程还是下降过程，并使用相应的逆模型计算出此时力矩促动器的补偿控制电压u（t）。最后通过闭环控制应变电压信号u（t），实现对力矩促动器电机输出力的补偿控制。

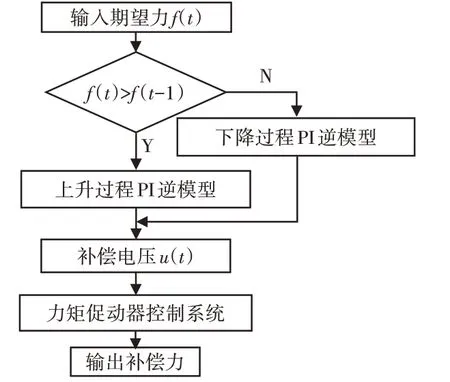
图7 力矩促动器补偿控制原理Fig.7 Compensation Control Principle of Warping Harness

4 实验验证

根据力矩促动器的工作原理，实验室研制了的力矩促动器实验模型，如图8所示。主要由基座、三条Whiffletree支撑轴、Whiffletree三脚架、弹簧叶片、电机输出轴组成，通过控制电机的输出位移，使弹簧叶片发生形变，弹簧叶片形变会在弹簧叶片的根部（与Whiffletree 三脚架连接处）产生一个力矩，此力矩会使三条Whiffletree支撑轴上支撑力重新分配，从而达到改变镜面面型的目的。电机输出轴上的每一个力都对应Whiffletree三脚架上的一组可以改变镜面面型的力，通过闭环控制电机输出轴上的力，可以达到期望的面型。

图8 力矩促动器实物图Fig.8 Material Object of Warping Harness

为了对力矩促动器进行测试和控制，搭建了基于DSP的力矩促动器控制系统，该系统以TMS320F28335为控制核心，一共有5路12位高精度AD通道，其中，1通道采集电机输出轴上的力、3通道采集三条Whiffletree支撑轴上的力，1通道采集应变片的输出电压。电机输出轴和Whiffletree支撑轴上各安装了力传感器，力传感器采用Interface公司的SM-200型力传感器，应变片采用Vishay公司生产的N2A-13-S5232K-350/E5型应变片。通过闭环控制应变片的输出应变电压，实时测量电机输出轴上的力和三条Whiffletree支撑轴上的力。

为了验证PI模型在力矩促动器控制系统的有效性，在通过对模型进行建模后，计算出逆模型的各项参数向量，然后将逆模型的补偿通过DSP控制系统来实现。将期望力通过上位机发送给DSP后，DSP根据力矩促动器前一时刻的运行状态和期望力，通过逆模型计算得出补偿电压，然后通过闭环控制应变电压来实现控制电机轴上力的输出，输出力的大小通过安装在电机输出轴上的力传感器来进行验证。

在本次实验中，通过上位机依次给DSP 发送0N 递增到80N 到力，然后再从80N 递减到0N，间隔为2N，先通过PI 逆模型得到补偿后电压的大小，然后通过闭环控制弹簧叶片的应变电压，使用PID 控制实时调节步进电机的运行频率，使弹簧叶片达到期望的应变，力矩促动器补偿输出结果示意图，如图9 所示。

图9 力矩促动器补偿控制输出Fig.9 Warping Harness Compensation Control Output

对比图9中的两条曲线，可以看出，经过PI逆模型校正的控制精度明显高于未使用逆模型补偿时的控制精度。使用逆模型补偿后的测量误差随校正力的变化的曲线，如图10 所示。通过与图6 中的PI 模型拟合误差对比可以看出，实际补偿误差略大于模型的拟合误差，因此，补偿控制后的输出力误差一方面来源于模型拟合时的误差，另一方面也与控制系统的系统误差有关。

图10 补偿控制后的误差曲线Fig.10 Error Curve after Compensation Control

补偿后误差的下降幅度，如表1所示。在上升的过程中，误差一直控制在很小的范围内，具有较好的补偿效果。下降过程的控制误差波动略大于上升过程。通过对误差的测量数据进行计算可得，未使用逆模型补偿时输出力误差的RMS值为1.888N，使用逆模型补偿后的RMS值为0.2596N，减少了86.25%，较好的提高了力矩促动器的控制精度。

表1 补偿控制后的误差Tab.1 Error Comparison before and after Compensation

5 结论

这里提出了基于PI模型的力矩促动器补偿控制方法，利用PI迟滞模型对力矩促动器的迟滞特性进行建模，通过LMS算法优化得出算子个数为25时建模效果最佳，然后使用逆模型对输入电压进行补偿，实现对力矩促动器输出力的高精度控制。经过逆模型补偿的电压-力控制系统的RMS值由原来的1.888N降低为0.2596N，最大相对误差由原来的4.073%降低为0.6375%。实验结果表明：对力矩促动器进行PI逆模型补偿可以有效降低输出力的迟滞误差，提高了力矩促动器的控制精度，在主动光学中具有一定的应用价值。