基于Workbench无避让立体车库结构优化分析

曾金传，张树房，赵海霞，管清正

（1.江苏联合职业技术学院，南京 210000；2.华晟（青岛）智能装备科技有限公司，山东青岛 266061；3.青岛科技大学机电工程学院，山东青岛 266061；4.青岛宏大纺织机械有限责任公司，山东青岛 266061）

0 引言

由于无避让立体车库的设计目标是在单位面积上存放更多数量的汽车，因此整体结构的稳定性能就显得尤为重要，在追求整体结构简便、轻量化的同时，也要保证结构的应力强度，合适的优化才是最好的改进，可以为大规模的产业化做好基础保证[1]。本文运用Workbench分析软件，对产品结构进行分析优化，为无避让立体车库的实际开发提供一种简单有效的方法。

1 结构设计与三维建模

通过对各种文献的综合查阅及对市面上常见车型尺寸数据的收集整理，确定出该无避让立体车库尺寸设计范围为5300 mm×2500 mm×2000 mm。通过前期的设计需求分析及市场调研[2]，整体采用钢结构的方式，不但可以满足使用要求，还能够降低成本，确定的无避让立体车库结构如图1所示。

图1 可移动式无避让立体车库

2 无避让立体车库静力学分析及结构优化

将设计完成的三维无避让立体车库结构图导入Workbench中进行静力学分析[3-4]，整体结构的材质为Q235，在三维模型导入之前对无避让立体车库进行简单的优化改进，将不会对整体结构产生影响的部分结构剔除掉，以减少软件的计算数据，快速计算出实验结果，软件计算的目的是验证设计初期整体的结构强度是否满足标准车型载重需求[5]。

2.1 施加载荷及划分网格约束

1）编辑材料参数。

定义材料参数如表1所示。

表1 无避让立体车库材料参数

2）定义接触。

在静力学分析的过程中是将整个车库三维立体结构直接导入到Workbench中，没有在软件中重新建模，整个模型的结构相对来说比较复杂，软件的运算量相对也比较大，因此需要将模型进行简化，尤其是一些接触副，可以设置为默认模式，这样可以减少软件计算时间，且对整个静力学计算精度不会产生影响。

由于汽车的发动机大多数是安装在汽车的前方，因此汽车前后两个轮胎各自承受汽车的整体的重力不一样，所以在4个轮胎与载车板的接触面分别施加0.255、0.255、0.17、0.17 MPa等4个载荷，如图2所示。采用定值网格划分的方式，按照网格大小为40 mm的网格对整个无避让立体车库进行网格划分，划分完成以后，总共生成204 193个单元格，节点416 869个。

图2 载荷及约束

2.2 有限元分析结果

有限元分析完成以后，在界面选择应力和变形求解模块进行最后的求解，得到应力和变形云图，求解结果如图3、图4所示。

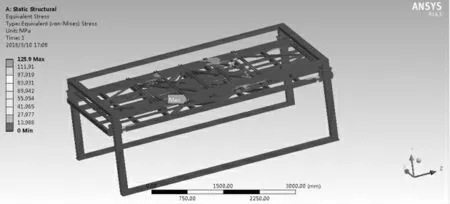
图3 整体应力求解结果

图4 整体变形求解结果

根据计算结果分析得出，在整个无避让立体车库结构中，车库的最大应力出现在载车板中间横纵梁交错的位置上，其应力值最大为125.9 MPa，该应力值与Q235的许用应力值相比还是比较偏低的。结构的最大应力值出现在这个位置也符合我们的预判，原因是载车板是一种框架式的构造，中间有旋转的支撑，两边为悬空结构，当车辆进到载车板上时，车的重力就会集中到载车板的两端，此处就会造成一定的应力集中。同时，从数据中可以得出变形量为6.74 mm，因此整体结构符合安全要求。

3 基于响应面法的整体车库结构优化

在目标优化的过程中，大量的变量同时不断变化会导致计算结果出现巨大的差异，因此在选择变量的时候，要将主要的变量挑选出来，不能把所有的数据全作为变量，同时应选择合适的输出变量，只有这样，才能找出一种合适的、最优的方式来实现对整个产品的优化[6]。

3.1 目标函数与约束条件

1）目标函数。

在优化设计的过程中，要将减轻无避让立体车库的整体质量作为首要的目标，同时还要在整个优化的过程中，保证车库整体的变形量在材料的一定的许用值之内，因此在本文优化设计的过程中，统一按照这一约束模式，将零部件的最大质量和最大的位移量作为整体的目标函数[7]：

式中：F1（x）=min Mmax，Mmax为整体的最大质量；F2（x）=min Tmax，Tmax为整体的最大位移。

2）约束条件。

由上文可知，首先在保证整体结构安全性的前提下，尽可能地减轻整体无避让立体车库的质量，从而实现产品的经济性能，因此在整体结构实际的过程中，主体框架采用标准的方钢设计，方钢的横截面的尺寸可以作为设计约束条件[8]：

由此得出多目标优化建立的优化模型为:

3.2 车库托盘结构优化

根据上文，将车库托盘的横向支撑杆横截面中的两个尺寸L18、V16，托盘纵向支撑杆中的一个尺寸L2，这3个尺寸作为约束尺寸，并建立相关约束方程，3个尺寸数据的相关位置如图5和图6所示。

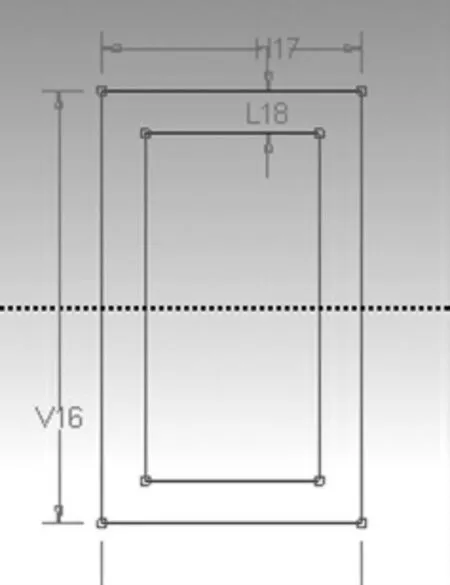
图5 托盘横向支撑杆

图6 托盘纵向支撑杆

1）建立约束函数。

根据上文中提到的目标函数及约束函数建立方程：

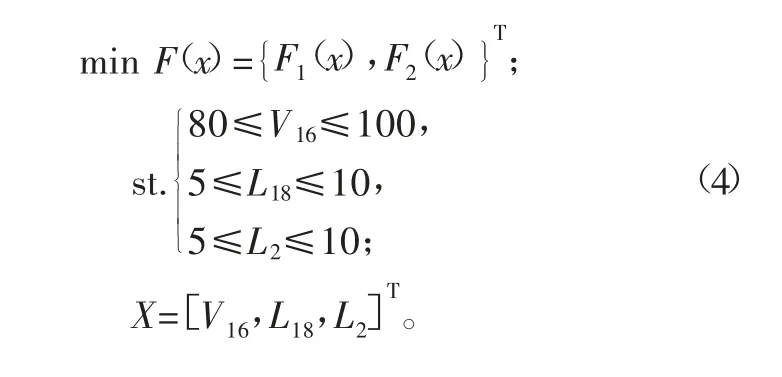
2）加载约束及求解。

对于无避让立体车库托盘，采用加密网格的方式，在划分网格的时候采用25 mm的间距来进行划分，其他部分按照原先静力学分析时的网格划分，同时施加的作用力也与静力学分析时施加的作用力相同。约束加载完成之后，进行分析求解，求解结果如图7、图8所示。

图7 设计参数对输出变量的敏感度

图8 各项最优解

从图7我们可以看出，3个尺寸对无避让立体车库的整体质量及整体结构最大变形量的影响是不一样的，在3个尺寸当中，对整个车库的质量影响最大的是尺寸L18，而V16对整个车库的质量和变形的影响不一。对于不同的约束参数，通过响应面法进行优化计算以后，分析计算得出的预测值与有限元实际计算分析得出的结果在相似度方面还是非常高的。因此，这也从另外一个方面证明响应面分析法[9]可以实现对车库外框结构的最大质量和最大变形的高度拟合，说明这种算法能够实现对结构不同尺寸的优化，已达到一个较好的输出结果。

根据计算结果（如图8），我们选择质量和变形都相对来说比较小的一组数据，作为最终的优化数据：L2=5.03，L16=97.5，V18=7.7。根据最终的计算结果，使得无避让立体车库托盘的质量由原来的1.3715 t降低到1.0585 t，质量减轻了22.82%，同时总的应力为172.28 MPa，总的变形为6.3719 mm，符合要求。

通过目标函数约束法，在进行优化的过程中，选择合适的约束数据可以有效地对目标结构进行尺寸优化，同时还能够保证整体的结构性能在一个安全的范围之内，实现了尺寸数据与目标值之间的有效联动，为优化设计提供了一条可靠之路。

3.3 其他重要尺寸优化

参照3.2节中的优化方法，分别对外框结构中的横杆和H型竖杆进行尺寸约束优化，如图9和图10所示。

图9 外框H型竖杆设计数据

图10 外框横杆设计数据

通过分析得出最优解结果如图11和图12 所示。

图11 各项最优解

图12 各项最优解

根据图11的计算结果得出，选择一组可以使无避让立体车库托盘质量和变形都有效降低的数据：H1=94，L4=5，V2=62。整个托盘的质量变成0.658 79 t，总变形为0.017 84 mm。

根据图12的分析得出：H1=88、H3=39、V2=62，可以让托盘的质量降低为0.575 63 t，总变形为0.016 099 mm。

通过以上的分析得出，进行响应面优化计算以后，无避让立体车库的外框可以从原来的0.971 51 t降低到0.575 63 t，质量减轻40.75%，质量减轻的同时，外框的整体结构应力及整体变形都符合Q235材质的要求，采用响应面分析法可以在很大程度上降低产品钢材的用量，降低生产成本。

4 结论

在初级的车库模型设计完成以后，通过Workbench的静力学模拟分析，得到等效应力云图，通过应力分布，查找不足，优化改进，得到初步满足要求的设计模型，再对模型进行优化分析，设定约束条件，确定输出指标。通过响应面分析法，优化结构中的关键尺寸，使无避让立体车库的整体质量由原来的3.5996 t降低为2.890 72 t，降低率为19.69%，使用响应面多目标优化法，可以更快、更有效、更便捷地实现降低产品材料用量、节省生产成本的目标，可以为设计人员提供一种简便的优化方法，缩短产品设计的时间周期，同时还能保证设计结构的整体可靠性与安全性。