基于ANSYS的梳齿塔库提升平台结构优化设计

胡亚男

（宝胜系统集成科技股份有限公司,江苏扬州 225819）

0 引言

近年来，随着我国社会经济高速发展，国内机动车保有量保持着高位增长，随之也带来了停车难等一系列问题，一定程度上制约了城市现代化发展进程。在智慧城市建设背景下，基于城市级智慧停车平台系统发展，大力推进智能化立体停车设备建设、精准增加城区停车位成为解决停车难问题的重要举措。在各类停车设备中，智能塔库停车设备具有占地面积小、土地利用率高、高效节能、安全可靠和稳定性高等独特优势，尤其适宜建立在高度繁华的城市中心区域，有效解决了中心城区的停车难问题[1-2]。

目前，对现有智能机械立体车库的提升系统、存取车系统、回转系统及电气控制系统等系统层面的理论分析研究较多[3-5]，而对系统中核心构件优化设计较少。通常情况下，此类受力构件是建立在设计者经验基础上进行，为保证足够的安全系数，实际设计构件结构尺寸偏大，存在一定安全冗余，同时也增加系统质量和制造成本。因此，借助三维建模软件及有限元分析软件研究系统关键受力构件，并结合优化设计方法快速确定合理的结构尺寸，对提高材料利用率、降低制造成本具有重要意义[6-8]。本文以智能塔库提升平台为研究对象，利用有限元分析软件ANSYS Workbench强大静力学求解分析功能，对提升平台结构进行静力学分析，在满足刚度、强度要求的前提下对提升平台核心受力构件进行结构优化改进，进而达到优化机械结构、降低制造成本的目的。

1 提升平台结构设计

智能塔库主要由提升系统、存取车系统、钢结构主体、回转系统、电气控制系统等组成。提升系统主要是完成载车提升平台在垂直方向上的上升与下降，将车辆提升至指定停放平层位置，主要包括曳引动力系统、提升平台、配重及配重导轨等。作为车辆进行升降运动的载体，提升平台的作用是承受汽车整体质量，配合曳引动力及配重将车辆垂直提升到指定的高度，以供横移机构将车辆放入停车位。而提升平台中固定梳齿是一种悬臂式受压构件，其设计是否合理直接影响到整个升降系统的安全可靠性，因此安全性要求最高，同时梳齿数量多、质量大，应用优化设计方法可以有效降低构件质量，达到轻量化设计的目的，使提升平台具有良好的实用性和经济性。

本文所研究的智能塔库设备，根据项目规划容车尺寸为长×宽×高≤5300 mm×1950 mm×1550/2050 mm，容车质量要求整车车重≤2350 kg。提升平台整体尺寸长×宽为6040 mm×2800 mm，主要是由提升梳齿架和提升叉臂对称安装形成完整的升降平台。梳齿结构通过梳齿的排布，实现汽车前轮位置定位，后轮无需定位以适应各种不同轴距的车辆。这种设计不仅能够保护车轮，也实现了汽车位置的准确定位。在三维软件Unigraphics NX中设计了提升平台方案，其中梳齿结构采用规格为60 mm×40 mm×4 mm 的矩形管与方钢相结合方式布置，其三维模型如图1所示。

图1 提升平台结构模型

2 提升平台有限元分析

2.1 提升平台受力分析

提升平台的功能是对存取的车辆进行升降运动，其在静止状态时所受的力主要是车辆的自重，其在运动的时候还受到惯性力的作用，因为运动速度较慢，所以可以忽略不计，因此仅需进行静力分析。为了简化计算，假定提升平台所受到车辆轮胎的作用力近似均匀分布，受力情况如图2所示。额定载车车重为2350 kg，按车辆的前后轮相距2800 mm，将汽车质量按分配比6∶4 分别分配在前后轮上，因此单个前轮所在位置的梳齿上所承载的力为7050 N，单个后轮所在位置的梳齿上所承载的力为4700 N。

图2 提升平台受力简图

2.2 有限元模型分析求解

1）模型导入及材料定义。选用静力学分析模块，将建立的立体车库模型存储为.x_t 格式，然后导入到ANSYS Workbench中建立有限元模型。为便于仿真模型建立及高效分析，对不影响分析的螺栓、滚轮等部件进行简化，根据提升平台的对称结构选择导入一半模型进行求解。在Engineering Data中对提升平台进行材料属性的添加，提升平台各部件所用到的主要钢材料为Q235及Q355，其力学性能参数如表1 所示，根据材料的性能参数在Workbench中设置提升平台各部件的材料属性。

表1 有限元模型材料参数

2）网格划分。在Mesh模块下，采用自动划分网格功能将所建立的提升平台模型进行划分，模型划分为210 481个单元和619 500个节点，经检验平均网格质量为0.877，网格质量较好，能够满足静力学求解要求。网格划分后如图3所示。

图3 网格划分模型

3）添加约束与施加载荷。根据实际工况对提升台进行约束以及施加载荷，利用Static Structural 下的Fix Support 约束，约束位置为提升平台叉臂两端的上表面，再通过Force对提升叉架梳齿上前后车轮对应的位置施加面力。

4）求解结果定义。在Solution中定义输出参数分别为Stress-Equivalent（von-Mises）和Deformation-Total，进行有限元模型的计算求解，从而得到提升平台的总体等效应力分布云图和变形位移云图。

2.3 分析结果

完成上述设置后提交模型求解，求解完成后在Solution中可以对分析结果进行查看，最终得到的应力云图和变形云图分别如图4和图5所示。

图4 提升平台应力云图

图5 提升平台变形云图

由图4可知，提升平台在纵向矩形管与梳齿连接区域处存在应力集中现象，最大应力位于提升叉架的梳齿结构上，其值为158.37 MPa。而梳齿所用材料的许用应力[σ]=355÷1.34=264.9 MPa，最大应力值小于许用应力值，因此提升平台在额定载荷作用下强度符合要求。由于该提升平台为悬臂式结构，要求在额定载荷下，悬臂端挠度不大于L/300，L即悬臂长度，因此梳齿的最大变形不大于1.87 mm。由图5可以看出，提升平台的最大变形值为0.882 mm，位于提升叉架的梳齿结构的悬臂末端，在许用范围内，满足提升平台的变形许可条件。

3 梳齿结构的优化设计

通过对提升平台结构受力分析可以看出，矩形管与方钢结合的梳齿结构，方钢原始设计尺寸偏大，留有较大的安全裕度空间，虽然满足了提升平台的性能要求，但是也增加了平台结构的用钢量和制造成本。因此，需要在保证提升平台结构刚度和强度满足要求的前提下，通过仿真软件对关键构件设计尺寸的快速优化，合理减少梳齿结构的质量，实现提升平台轻量化，同时降低生产成本，提升产品综合竞争力。

本文以提升平台的关键受力构件梳齿方钢为进一步的优化对象，梳齿结构如图6所示。选取4个主要结构尺寸作为设计变量；梳齿方钢与纵梁矩形管焊接区域长度L1，梳齿方钢焊接端截面高度H1，悬臂端截面高度H2及方钢宽度D1。将梳齿的质量m、最大变形量δ、最大等效应力σ作为多目标优化变量。

图6 梳齿结构示意图

优化基本思路如下：在ANSYS Workbench 的Design Exploration模块下选择响应面优化分析工具，首先选取中心复合试验获得多组试验点，定义设计变量范围、状态变量约束条件及多目标函数；其次以Kriging 插值法作为响应面拟合函数，经仿真迭代计算获得优化的响应面模型；最后以响应面模型为基础，通过多目标遗传算法（MOGA）寻找多个优化目标的帕累托优化解集（Pareto Solution），并根据实际需求从解集中选取最优响应值作为最终优化结果。

3.1 响应面法模型建立

建立精确、合理的响应面模型，首先要明确设计变量和目标变量，并选用合适的试验设计方法构建所需的试验点，建立目标变量与设计变量之间的函数关系，从而求解精确的多项式目标表达式[9]。在实际工程应用中，考虑到响应面模型精度需求和计算成本，目标变量与设计变量之间的响应面模型函数关系可表示为

式中：y为响应预测值；xi和xj为设计变量；n为设计变量个数；β0、βi、βii、βij分别为偏移项、线性偏移系数、二阶偏移系数和线性交互效应系数；ε为拟合精度误差。

在ANSYS Workbench中选取循环次数少、运算效率高的中心复合设计作为试验设计方法，设计变量共有4个，共产生了26个实验点。将梳齿的质量m、最大变形量δ、最大等效应力σ作为目标变量，选用Kriging插值法构建梳齿结构优化的响应面模型。

为便于响应面优化，确定设计变量对目标变量的重要程度，将上述4个设计变量对梳齿质量、最大变形量和最大等效应力的影响程度进行灵敏度分析，其分析结果如图7所示。

图7 响应面模型灵敏度图

由模型的灵敏度柱状图可知，设计变量L1对最大变形量的灵敏度为-0.212%，对最大应力值的灵敏度为-5.324%，对质量的灵敏度为0.113%，说明该变量的调整对提升平台结构的3个目标函数影响极小；设计变量H1对最大变形量、最大应力值和质量的灵敏度较为显著，分别为-67.62%、-66.73%和34.655%，说明该变量的增加将使变形量和应力值降低，质量增加；设计变量H2与变形量成负相关，与最大应力和质量两项输出参数成正相关，对质量影响较大；而设计变量D1对3个目标函数的影响趋势与H1相同，但最大变形量、最大应力值的灵敏度值较低，影响力较小。

3.2 响应面分析

通过对上述响应面模型灵敏度图的分析，选取对每个目标函数影响较为显著的两个设计变量并分别生成响应曲面，用来观察设计变量对目标函数影响的变化趋势，如图8所示。

图8 目标函数的响应面曲面

通过响应曲面分析，可以直观地看出不同的设计变量的变化对目标函数的影响趋势，并根据趋势分析结果为结构设计参数的优化选择提供参考。从变形量的响应曲面可以看出，H1、H2与变形量成非线性关系，变形量值随着H1、H2增大而增加；由最大等效应力的响应曲面分析可以得出，H1、H2与应力成非线性关系，随着H1的增大，应力值增加，随着H2的增大，应力值会有所降低；由质量的响应曲面分析可知，设计变量H1、D1与质量成线性关系。

3.3 梳齿结构多目标优化

对提升叉架梳齿优化的主要目的是实现提升平台的轻量化设计，即在综合考虑超载、偏载等特殊情况下，减轻提升平台钢材使用的总质量的同时需保证结构的受力性能满足车库正常运行使用要求。因此以提升叉架梳齿质量最小、刚度最优、强度最大为目标函数。因此可定义优化的数学模型如下：

ANSYS Workbench 提供的多目标遗传算法（MOGA）具有收敛性、鲁棒性好且能够并行处理等优势，支持复杂工程多目标问题的优化求解，适合计算全局最优值，可规避局部最优的陷阱，因此应用领域广泛[10-12]。将上述优化模型应用软件MOGA多目标遗传算法求解Pareto最优解集，定义求解参数如下：初始种群规模为4000，每次迭代样本数为800，最大迭代次数为20，收敛标准为0.8，候选点数为3。经10 596次迭代后收敛，得到Pareto优化前沿解，如图9所示。

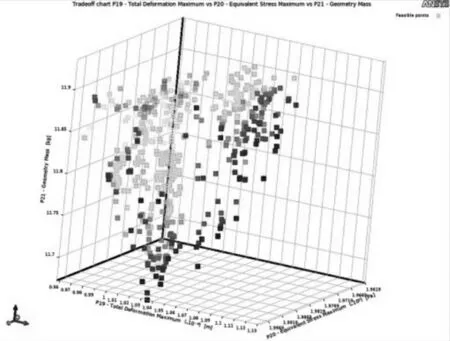
图9 Pareto优化前沿解

由于多目标优化问题存在多个目标函数，无法通过一组设计变量能够使得所有的目标函数都得到最优值。因此，多目标优化算法得到的通常是一组最优解集，需要结合实际工程应用，折中选取满足应用要求的优化解，使各目标函数尽量满足设计目标。通过对比候选点结果，以满足提升平台安全稳定为前提，综合考虑提升平台轻量化，选择候选点参数组合（L1=110.330 mm，H1=73.106 mm，H2=30.234 mm，D1=41.196 mm）作为多目标优化解。对设计参数进行圆整处理后，在静力学模块求解得到优化前后性能参数，如表2所示。由对比可知，优化后的梳齿结构最大变形量及最大等效应力值均有增加，但都在安全范围以内，而优化前后梳齿的质量由14.711 kg 减少为11.709 kg，减少的质量是优化前的21.41%，实现了提升平台结构轻量化设计的目的。

表2 提升梳齿结构优化前后结果对比

3.4 优化结果验证

通常情况下，驾驶员需根据车库内部引导屏操控车辆停放在提升平台中位，以保证提升平台两侧提升叉架受力平衡。但也会发生因驾驶员个人操作不当等原因将车辆停放在偏向提升平台某一侧的提升叉架，导致提升叉架受力不均匀，因此在对优化后的升降台进行静力分析时选取偏载工况进行荷载受力校验。基于优化后的梳齿结构进行偏载受力分析，得到提升平台偏载状态应力云图及变形云图，如图10和图11所示。偏载工况下，优化后的提升平台最大等效应力为209.76 MPa，最大变形为1.306 mm，满足结构强度及刚度要求。

图10 提升平台偏载应力云图

4 结论

1）以智能梳齿塔库的提升平台为研究对象，在Unigraphics NX三维软件中建立实体模型，并在ANSYS Workbench对有限元模型进行受力模拟，得到最大等效应力为158.37 MPa，最大变形量为0.882 mm，分析结果表明该提升平台满足强度和刚度要求。

图11 提升平台偏载变形云图

2）在原模型基础上对提升平台的关键受力构件梳齿进行优化设计，采用中心复合试验构建Kriging 响应面模型，并选取多目标遗传算法（MOGA）完成自主寻优，得到优化的梳齿结构，优化前后单条梳齿的质量由14.711 kg减少为11.709 kg，质量降低约21.41%，实现了提升平台结构轻量化设计的目的。

3）基于优化后的梳齿结构进行提升平台的偏载受力分析，优化后的提升平台的最大等效应力为209.76 MPa，最大变形为1.306 mm，满足结构强度及刚度要求。验证结果表明有限元仿真分析、试验设计、响应面模型和多目标优化算法的结合可有效应用于智能机械车库关键受力构件的多目标优化。