动态环境下的机器人平滑自适应变阻抗控制

林壮，张朝霞，张宁，黄挺博，欧道江

（1.佛山科学技术学院机电工程与自动化学院，广东佛山 528225；2.佛山智能装备技术研究院，广东佛山 528234）

0 引言

随着机器人技术的发展、机器人位置控制精度的提升，在工业接触式作业过程中，机器人需要进行精确的位置控制的同时，还需要对机器人进行精确的接触力控制。然而在工业接触式作业时的机器人所面临的往往是动态的或者是非结构的环境，当机器人与环境接触的过程中，机器人移动速度过快和微小的位置偏差可能会导致过大的力冲击。

一些学者围绕力冲击问题进行了深入的研究。文献[1]将视觉和阻抗控制相结合，提出一种非接触阻抗控制的方法，利用视觉信息来调整机器人和环境之间的虚拟阻抗，由虚拟阻抗产生的虚拟接触力来调节机器人的运动轨迹，从而实现对机器人瞬间接触力的控制。文献[2]提出一种改进的阻抗控制器，结合非线性PID控制策略对接触力进行补偿。文献[3]、[4]基于机器人能量转换的思想，提出一种在线最优切换阻抗控制参数方法来最大化减小接触力冲击。上述文献中所提方法，结合精确的机器人系统模型，都可以有效地解决机器人系统空间转换时接触力冲击问题。为了在阻抗控制中更好地发挥机器人位置控制方法的优势，文献[5]中针对平面和曲面型作业对象，重点研究离线轨迹方向纠偏方案，提出一种结合定阻抗控制和基于力反馈的轮廓跟踪策略的恒力控制算法，所设计的控制策略具有一定的柔顺性，但对于接触力的跟踪精度仍不是很理想。

考虑到上述方法存在的一些问题和缺点，本文借鉴自适应变阻抗的研究思路，结合自抗扰控制，提出了基于位置的平滑自适应阻抗控制方法用于实现动态环境下机器人系统在自由空间和约束空间中的位置和力跟踪控制。

1 机器人与环境的接触过程及模型

机器人和机器人之间相应的接触力环境如图1所示。碰撞阶段是机器人从自由运动到接触的必然过程控制，碰撞时间是瞬态的，这将产生极端的接触力[6]。此外，振荡和力太大过冲会导致系统不稳定，甚至更多严重后果。

图1 机器人与环境接触过程

1.1 安排过渡过程

安排过渡过程[7]主要是用来解决机器人在由自由空间向约束空间转换时带来的力冲击问题。通过分析和实验得出，合理地安排过渡过程使期望力缓慢能够有效减小空间转换带来的力冲击。

安排过渡过程可以使用多种形状的曲线，本文中使用ADRC中的最速微分跟踪微分器来安排过渡过程，包括非线性和线性形式。

非线性表达数学表达形式：

式中：Fd为期望力的大小；λ为采样周期；r0为过渡过程的长短，r0与过渡过程时间成反比；v1为过渡过程输出期望力；v2为过渡过程输出期望力的微分。

ADRC的过渡过程线性形式仿真图如图2所示。

图2 安排过渡过程（线性形式）

1.2 机器人与环境接触力模型

传统的阻抗控制是最初是由Hogan[8]提出的。通常，考虑一维方向上的阻抗控制，阻抗控制的传递函数为k（s）=1/（ms2+bs+k）。它描述了力误差ef和位置扰动e，可以表示如下：

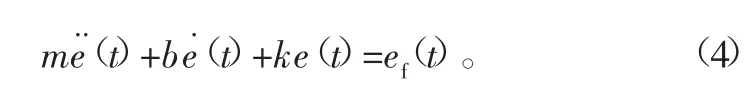
位置扰动e与参考位置轨迹pr叠加后，可得到发送给机器人的轨迹pd=pr+e=pr+efk（s）。

将环境等效为一阶刚度为ke的线性弹簧系统，环境位置用pe表示，机器人末端实际位置用pd表示，则机器人在与环境接触过程中产生的接触力可表示为

由上述假设可得力误差为

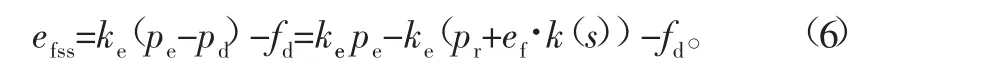
将k（s）=1/（ms2+bs+k）代入式（6）中可得控制系统在稳态情况下力跟踪误差：

可得当满足下列以下条件之一就可以使得力稳态误差efss=0，即t→∞时fe→fd。

在真实环境中，很难精确获得环境刚度ke和环境表面位置pe，因此难以使得力稳态误差efss为零，导致达不到跟踪期望力的效果。将上述阻抗控制刚度系数k设为0，可满足任何动态刚度下的理想跟踪性能环境。

因此，依靠式（8）、式（1）中的阻抗函数可以改写为去除阻抗刚度系数：

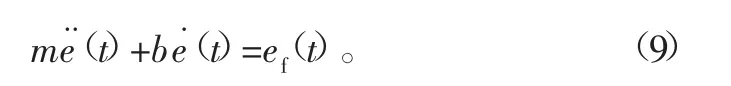
2 自适应阻抗控制及其稳定性分析

2.1 基于位置的自适应阻抗控制

实际复杂的环境模型往往是非线性模型，而不能简单地用线性弹簧来描述；在面对非线性模型的情况下，传统的定阻抗控制因没有动态适应性而致使力跟踪效果变差。为此，甘亚辉等[9]根据文献[10]所提出的基于位置的变阻抗控制的思想,针对环境动态变化情况下，提出了一种改进的自适应变阻抗力跟踪算法实时对阻尼参数进行自适应调整，如式（10）、式（11）所示：

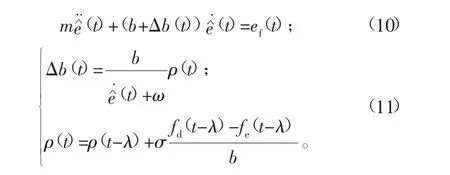
整个机器人闭环控制图如图3所示。

图3 机器人阻抗闭环控制图

由于一般情况下初始状态ρ（t-nλ）=0，联立式（10）、式（11）、式（13），重新整理可得

对式（14）进行拉普拉斯变换，自适应阻抗控制器稳态传递函数如下：

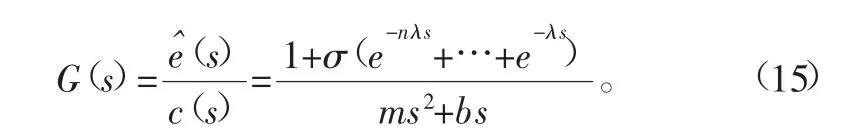
当采样时间λ足够小并且当n趋于无穷大时，满足

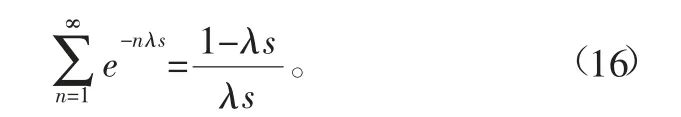
因此自适应阻抗控制器传递函数可改写，并进行重新整理得

给出图3中整个闭环的力误差传递函数φ（s）系统如下：

考虑几种常见的动态环境情况：阶跃信号R（s）=1/s，斜率信号R（s）=1/s2，正弦信号R（t）=sin ωt。自适应变阻抗控制器的稳态误差如表1所示。此外，对于复杂的环境，例如正弦情况环境下，需要通过减小σ来减小跟踪误差。

表1 自适应变阻抗的稳态力跟踪误差

因此，参考文献[11]，将σ的更新率公式设为

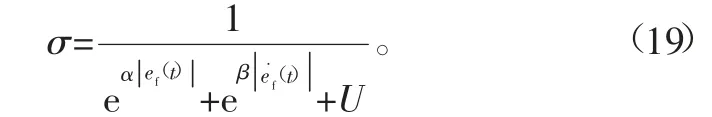
2.2 自适应变阻抗控制的稳定性证明

下面给出自适应阻抗控制器的稳定性证明[9]，并确定σ可调范围的值。将式（11）代入式（10）得到

由于一般情况下初始状态为0，即ρ[t-（n+1）λ]=0，联立式（13）、式（23），重新整理可得

因此其特征方程为

将式（16）代入式（25）可以得到

根据劳斯准则，劳斯表可表示为

为保证系统的稳定性，系数第一列和特征方程的系数必须为正，表示为：

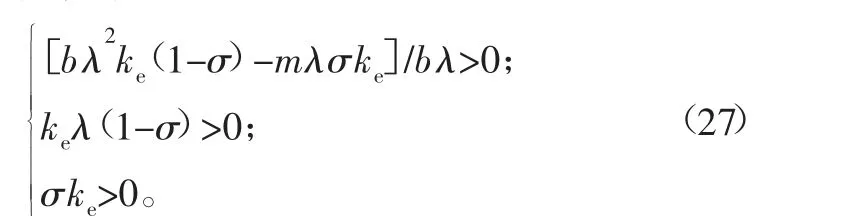
因此保证系统稳定的σ的取值范围为

联立式（28）和式（19）可以求出

因此，可以设定U=（m+bλ）/bλ。对于稳定的系统，根据拉普拉斯变换的稳态误差的定义，系统的稳态误差ess为

由此可知当t→∞时，fe→fd，即可以实现接触力fe对期望力fd的跟踪。

3 平滑自适应变阻抗控制器仿真及实机验证

3.1 仿真实验

为验证本文所提出的平滑自适应变阻抗力跟踪控制方法的鲁棒性，下面通过2个不同的仿真实验对文献[9]所提出的自适应变阻抗控制器、文献[11]所提出的预PID自适应混合阻抗控制器与本文所提出的平滑自适应变阻抗控制器进行力跟踪算法的测试和对比。现使用Matlab Simulink进行算法对比仿真实验，控制系统仿真参数的阻抗参数设定如下：t=0.004,m=1,b=60,k=0,α=1,β=1，文献[9]中控制器参数设置为σ=0.005，文献[11]中控制器的参数设置如下：kp=3.5，ki=0.03，kd=0.02。本文所使用的线性微分跟踪器中的参数设置如下：λ=0.004，r0=100。假设期望力输入为：

为验证3种控制器的力跟踪效果，假设摩擦力Ff的形式为cv=1.0 N·s/m和Fc= 3 N作为黏性系数和库仑摩擦：

为验证3种控制器对变化的环境刚度是否具有鲁棒性，ke的值如下所示:

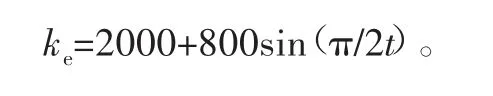
实验1假设接触环境为斜面，即x˙e≠0，x¨e=0。图4、图5和图6是文献[9]自适应变阻抗控制器、文献[11]PID自适应混合阻抗控制方法和本文平滑自适应变阻抗控制方法仿真结果对比图。图4（a）、图4（b）分别表示3种控制器斜面位置以及力跟踪效果对比图。图6（a）表示文献[11]和本文控制器跟踪斜面位置自适应调整因子σ变化图。

图4 斜面环境位置/力跟踪仿真对比图

通过仿真结果对上述所提到的3种控制器进行比较，从图5中可以看出，当环境为斜面，环境刚度时变，期望力跳变的情况下，文献[9]和文献[11]的控制器存在较大的力冲击，本文所提出控制器的力冲击较小，并且能够平滑过渡到期望力。此外，从图6（a）中可知本文中控制器比文献[11]控制器达到期望力稳定值的调节次数要少。因此，对于接触环境为斜面的情况下，本文所提出控制器相比于文献[9]和文献[11]的控制器表现出优势。

图6 斜面/正弦环境自适应因子σ仿真对比图

实验2假设接触环境为正弦曲面，即x˙e≠0，x¨e≠0。同实验1一样，将3种控制器进行仿真对比。图5（a）、图5（b）分别表示3种控制器力跟踪和正弦位置跟踪效果对比图。图6（b）表示文献[11]和本文控制器跟踪斜面位置自适应调整因子σ变化图。

图5 正弦环境位置/力跟踪仿真对比图

由图5可知，当环境为正弦曲面，环境刚度时变，在期望力跳变的情况下，文献[11]的控制器存在接触力振荡和较大的力超调，相对于文献[9]的控制器，还是能够取得比较好的力跟踪效果。而本文所提出控制器的表现在减小力冲击和力跟踪效果优于文献[9]和文献[11]控制器，并且由图6（b）中可知本文控制器比文献[11]控制器所达到期望力稳定值的调节次数要少。

由上面的综合仿真结果可以知道，本文所提出的控制器可以获得比文献[9]和文献[11]的控制器更好的控制性能，并且能够有效地减小机器人在空间转换时的力冲击。

3.2 实验验证

为了进一步验证所设计的平滑自适应变阻抗控制方法的有效性，本节分别进行摩托车架定点和动态打磨实验验证和分析。实验硬件平台是由HSR-JR680机器人和自主研发机器人磨抛设备组成的机器人磨抛系统平台，软件平台为Codesys工业运动控制平台，在外围磨抛设备上，底部装有S型拉压力传感器，用于测量实际打磨力，伺服驱动器与控制器通信方式为EtherCAT。系统示意图如图7所示，磨抛系统力控制框架图如图8所示。

图7 机器人磨抛系统示意图

图8 机器人磨抛系统力控制框架图

下面通过2个实验验证平滑自适应变阻抗算法的可行性。

实验1：定点打磨力跟踪实验。首先机器人手持摩托车架工件到达示教姿态点位保持不变后，外围磨抛设备开启平滑自适应变阻抗控制向前运动，测试场景如图9（a）所示。具体参数设置如下t=λ=0.02，m=1，b=40，k=0，α=0.7，β=1，r0=40，测试过程中，期望力分别设置为30、50、70 N。

图9 打磨实验场景示意图

实验结果如图10所示，由图10可知，平滑自适应变阻抗控制算法均能达到较好的恒力跟踪效果，经过对力数据的分析可知，定点打磨时力稳态误差在±0.6 N左右。

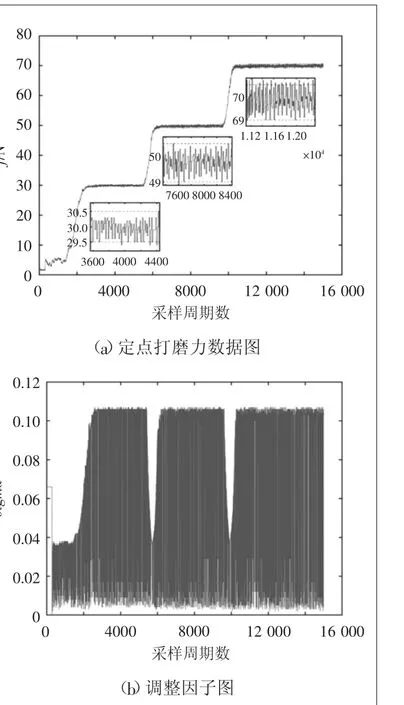
图10 实验1 测试结果图

实验2：动态恒力打磨实验。首先机器人手持摩托车架工件到达示教姿态点位后，外围磨抛设备开启力控制向前运动，在打磨过程中机器人根据示教好的轨迹运动，测试场景如图9（b）所示，t=λ=0.02，m=1,b=70，k=0，α=0.9，β=0.9，r0=35，期望力设定为30 N。

实验结果如图11所示，由图11可知，在机器人实际动态打磨过程中，实际接触力没有明显的力冲击，能够较为平滑地过渡到预期的期望力，并且达到预期恒力跟踪效果，经过对力数据的分析可知，动态打磨时力稳态误差在±0.9 N之内。

图11 实验2 测试结果图

4 结语

在本文中，针对机器人磨抛任务过程中空间转换导致的力冲击和环境不确定性的接触力跟踪问题，使用自抗扰中的过渡过程和自适应阻抗控制相结合，提出一种动态环境下的平滑自适应变阻抗控制方法，对该算法给出稳态误差分析及稳定性证明，对已有的两种自适应阻抗和本文所提的平滑自适应变阻抗进行了多种动态环境下的仿真实验对比，最后进行了平滑自适应变阻抗控制算法的实机验证，结果表明平滑自适应变阻抗控制算法能够有效减小空间转换带来的力冲击和能够达到预期的力跟踪效果，具有良好的鲁棒性。