金属橡胶非对称迟滞回线动力学建模研究

曹凤利，宋彬，王怀光，刘金华

（陆军工程大学石家庄校区,石家庄 050003）

0 引言

金属橡胶是由细金属丝经过缠绕、编织、成型、热处理等工艺制备而成的多孔材料。制备成型的金属橡胶构件可替代传统的橡胶减震元件，解决其存在的不耐高低温、真空中易挥发、减震频带窄、承载能力低等问题。金属橡胶适用于国防工业、航空航天、交通运输、石油化工等多种场合的苛刻环境，是一种应用范围广、特性优良的多功能减震材料[1-2]。

金属橡胶在变形时，其内部勾连交错在一起的金属丝会产生变形和滑移，变形形成弹性力，而滑移摩擦形成阻尼力，两种力相互作用即表现为宏观上金属橡胶的弹性恢复力。金属橡胶恢复力的特性与构件成型工艺、加载方式、金属丝材质、金属丝物理参数等因素密切相关[3]。在外激励的作用下，金属橡胶恢复力曲线（迟滞回线）与位移变形一般为非对称关系，工程上为了简化计算，可将其近似按对称曲线处理，但在非对称性较强时，这种近似的对称处理已不适于金属橡胶非线性动力学特性的描述[4]。目前，用于描述金属橡胶对称迟滞回线的数学模型主要包括双折线模型、迹法模型和混合阻尼模型等[5]，而非对称迟滞回线为特殊形态的非线性曲线，数学建模难度大，分析困难，因此相关的研究较少[6]。

本文在参考前期钢丝绳研究成果的基础上，探索并提出了一种描述金属橡胶非对称迟滞回线的数学模型。该模型较好地反映了迟滞回线的非对称性，为金属橡胶非线性动力学特性分析提供了新的方法。

1 金属橡胶非对称迟滞模型的建立

1.1 钢丝绳非对称迟滞模型

Y. Q. Ni[7]对钢丝绳的迟滞特性进行了深入研究，提出了非对称迟滞模型，即：

由于模型（4）中包含结构复杂的非线性微分方程，加大了其分析难度。为此，吴善跃等[7]对该模型进行改进，将时间参数去掉，增加了一个常数项，从而简化该模型。吴向荣等[8]又进一步将z（t）项由混合阻尼因子代替，简化为另一种形式的模型。

鉴于金属橡胶与钢丝绳在阻尼产生的机理上具有一定相似性，故以吴善跃、吴向荣等的研究成果为基础，结合金属橡胶构件的特性对该模型开展进一步的应用研究。

1.2 改进的金属橡胶非对称迟滞模型

由于z（t）+F1a（t）项是奇函数，表示关于原点对称的迟滞曲线，因此该式可用金属橡胶对称迟滞模型代替。目前，迹法模型是金属橡胶对称迟滞模型中应用较广的一种[5]，它采用多项式函数拟合金属橡胶恢复力曲线，并通过参数识别确定各项参数。恢复力曲线分为上下两支，其上支曲线多项式函数表示为

而下半支曲线由位移的反对称关系确定为

式中：k1、k3和k5分别为线性、三次和五次刚度系数；c和α分别为阻尼系数和成分因子。

由于迟滞曲线不一定在中心坐标原点，因此引入参数a，由式（10）得

式中，a、b为模型参数。

式（11）即为金属橡胶非对称迟滞模型。

2 金属橡胶非对称迟滞模型参数的识别

2.1 参数a、b的识别

金属橡胶典型的非对称迟滞回线如图1 所示。由于非对称模型式（11）中包含指数项，识别难度大，常规参数识别方法存在求解失败的情况，因此参数a、b的识别采用参数分离识别的方法，具体参见文献[7]。

图1 金属橡胶非对称迟滞回线

2.2 参数k1、k3和k3的识别

对经分离变换后的数据（xi＇，Fi＇）进行最小二乘五次多项式拟合，得到幂函数多项式：

式中，k0、k1、k2、k3、k4、k5为多项式系数，而奇数项即为弹性恢复力的刚度系数。

2.3 参数c和α的识别

用已识别出的k1、k3、k5及数据xi＇，即可重构非线性弹性恢复力Fk＇（xi＇）为

由式（14）和式（8），采用一般参数识别方法即可识别出系数c和α，识别分解后的迟滞回线如图2所示。

图2 迟滞回线的分解

3 金属橡胶动态试验及模型验证

3.1 金属橡胶试验系统

测试试验系统（长春试验机厂）包括试验机（PLS-20）和采集系统（DH5936）两部分，可实现最大载荷为20 kN、最高频率为40 Hz的动态位移（±50 mm）加载试验。

试验金属橡胶构件为圆盘形，采用奥氏体不锈钢丝（材质：0Cr18Ni9Ti，直径：0.3 mm，密度：7.9 g/cm3，弹性模量：198 GPa）制备而成，如图3（a）所示。

试验夹具结构形式如图3（b）所示，主要由托盘（夹具固定端）、垫片、压板、固定螺栓、螺母、拉杆（振动输入端）组成。金属橡胶构件位于托盘和压板之间，试验时的动态力由拉杆引入，带动金属橡胶构件产生结构变形。

图3 金属橡胶构件及夹具

3.2 模型验证

为了验证所建模型及参数识别方法的有效性，对圆盘形金属橡胶构件进行频率为5 Hz，预载分别为0.1、0.3、0.9、0.6 mm，振幅分别为2.0、4.1、4.8、5.1 mm的动态恒位移正弦加载。

为判定金属橡胶迟滞回线的非对称性，引入非对称因子λ，即

式中，FA、FB为位移幅值时的恢复力。

对不同振幅最大位移处的恢复力值进行计算，根据式（15）得到振幅为2.0、4.1、4.8、5.1 mm时构件的非对称因子分别为0.0336、0.0527、0.3378 和0.1516，可见上述恢复力曲线均为非对称曲线。

从试验中提取采样信号xi和Fi，利用编制的参数识别程序进行参数识别，结果如表1所示。得到的金属橡胶迟滞回线的理论预测曲线与试验曲线的对比如图4所示。

表1 模型的参数识别结果

通过参数拟合，得到各振幅时金属橡胶构件的非对称动力学模型，由图4可以看出不同非对称因子下的模型理论预测结果与实验结果有较好的一致性，基本反映了非对称迟滞回线的特性，表明本文所提出的理论模型是可靠的，能够满足工程应用的要求。

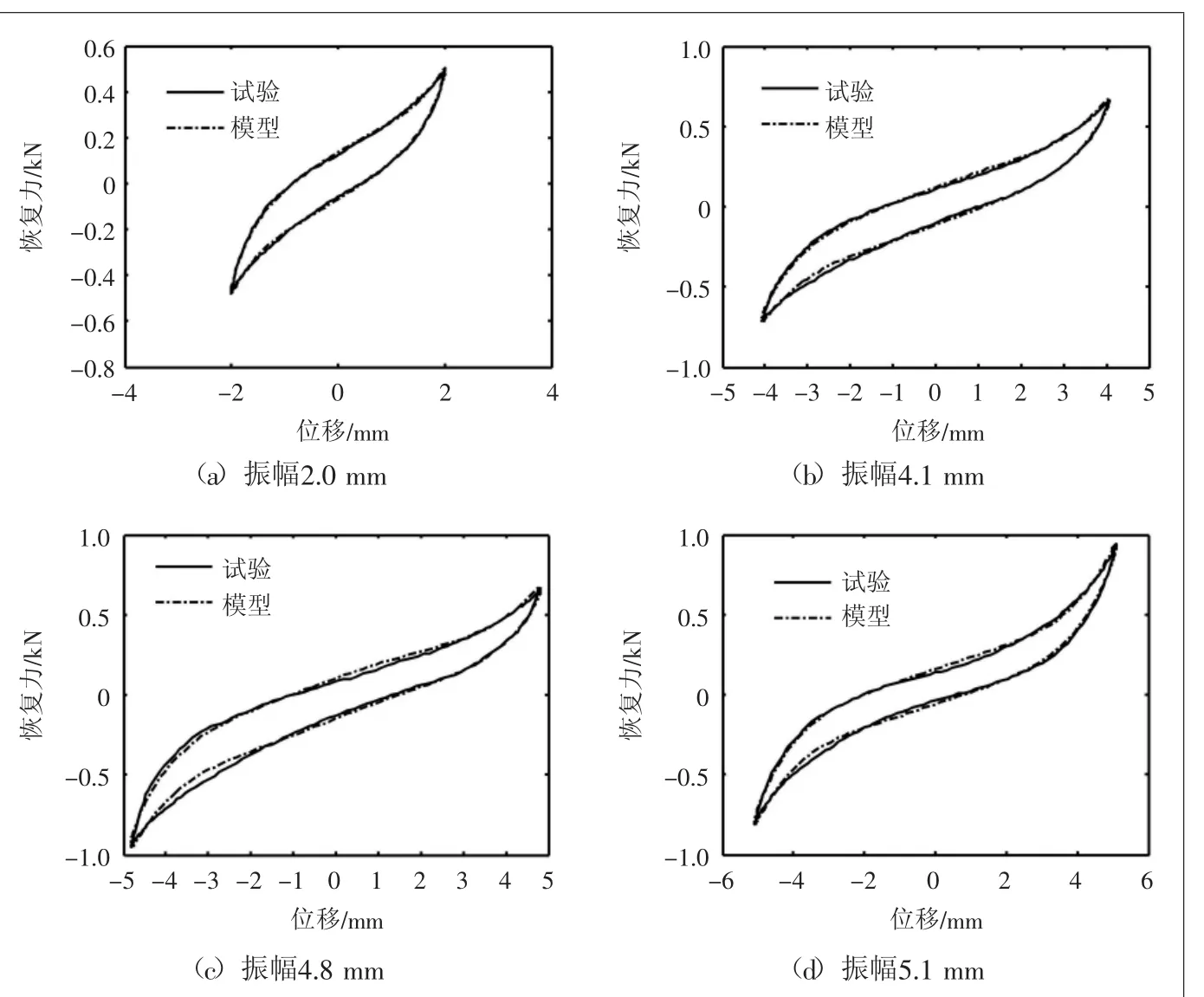
图4 模型预测与试验结果对比

4 结论

针对金属橡胶迟滞回线的非对称特性，在分析钢丝绳非对称迟滞模型的基础上，结合用来表示对称迟滞回线的迹法模型，建立了一种新的用于描述金属橡胶非对称迟滞回线的数学模型。采用参数分解和最小二乘法对具有不同非对称因子λ的圆盘形金属橡胶构件的非对称迟滞回线进行参数识别，由参数识别结果得到理论模型，将理论曲线与试验曲线对比，发现两者吻合较好，反映了迟滞回线的非对称特性，证实了模型具有一定的可靠性。该模型的提出为金属橡胶非线性迟滞特性的动力学分析提供了新方法，对指导金属橡胶的产品设计具有重要的价值。